Navier-Stokes方程式について,研究でCFDを使うことになった大学院生の役に立つような説明を行う
はじめに
この記事の内容は以下の前提に基づいている
- 非圧縮性流体の乱流流れ
- 密度\(\rho\),粘性係数\(\mu\)は一定
- 熱移動はなし
- CFDを研究で使う大学院生に必要な知識に重点を置く(ググって得られる知識と専門書の中間くらい)
参考文献はこちら
また,初学者のために,できるかぎり数式はベクトル表記とテンソル表記を併記するようにする
数値流体力学で必須のテンソル解析についての知識はこちら
流れの数値シミュレーションの概要
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(1)に関連して,流れの基礎方程式と基礎方程式のモデル化の概要について説明する
流れの基礎方程式
密度\(\rho\),粘性係数\(\mu\)が一定な非圧縮性流体の基礎方程式は,連続の式(質量保存式)およびNavier-Stokes方程式(運動方程式)である
連続の式は次の式で表される
\begin{equation}
\nabla\cdot\mathbf{u}=0
\end{equation}
\begin{equation}
\frac{\partial u_{i}}{\partial x_{i}}=0
\tag{1}
\end{equation}
Navier-Stokes方程式は速度3成分に対してそれぞれ1つずつ方程式があり,まとめて次の式で表される
\begin{equation}
\frac{\partial \mathbf{u}}{\partial t}+\nabla\cdot\left(\mathbf{uu}\right)=-\frac{\nabla p}{\rho}+\nu\nabla\cdot\left\{\nabla\mathbf{u}+\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\right\}+\mathbf{f}
\end{equation}
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial p}{\partial x_{i}}+\nu\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)+f_{i}
\tag{2}
\end{equation}
ここで,密度\(\rho\)と動粘性係数\(\nu\)は水や空気などの物性値,外力項\(f_{i}\)は重力などの影響である
速度\(\mathbf{U}\)の3つの成分\(U_{i}\)および圧力\(p\)をあわせたの4つの未知数に対して,速度と圧力を変数とする方程式がちょうど4つあるので,これらの方程式を解くことですべての物理量を求めることができるということがわかる
Navier-Stokes方程式の導出についてはこちらを参考
≫ナビエ-ストークス方程式の導出 _ 高校数学の美しい物語
Navier-Stokes方程式は,時間項(非定常項),対流項(移流項),圧力項,粘性項(拡散項),外力項の5つに分けられる
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial p}{\partial x_{i}}+\nu\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)+f_{i}
\tag{2}
\end{equation}
各項の名前と,どのようなはたらきを持っているかはなんとなくでも理解しておくといろいろと便利
時間項
\begin{equation}
\frac{\partial u_{i}}{\partial t}
\end{equation}
時間の経過に伴う流れの変化を表す項
定常計算では0となる
対流項
\begin{equation}
\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}
\end{equation}
流れが流れ自身の影響で運ばれていく効果(移流)を表す項
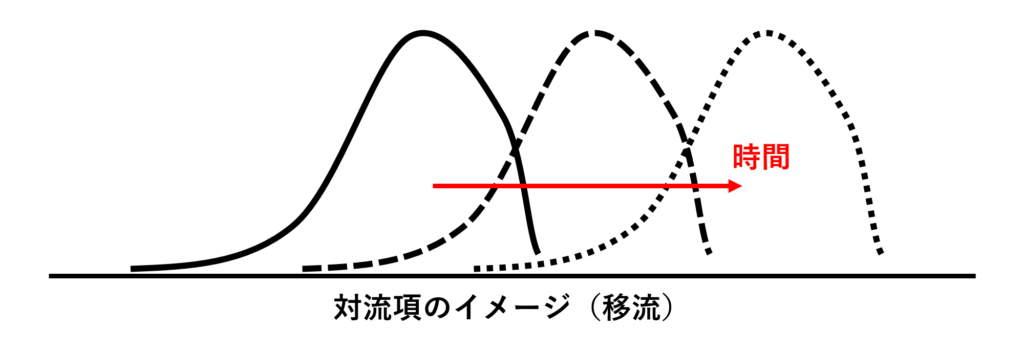
速度の2乗が現れる非線形項であるため,離散化の際に慎重に取り扱う必要がある
圧力項
\begin{equation}
-\frac{1}{\rho}\frac{\partial p}{\partial x_{i}}
\end{equation}
圧力差が流れに及ぼす影響を表す項
粘性項
\begin{equation}
\nu\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
\end{equation}
粘性によって流れの分布が平滑になる効果(拡散)を表す項
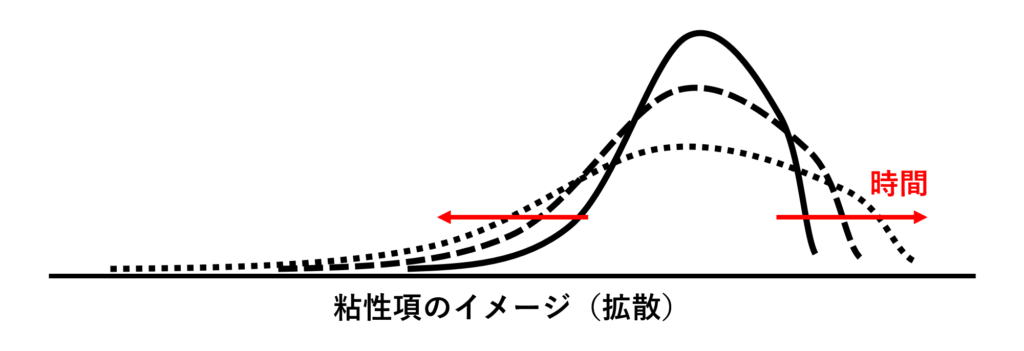
数値解析の計算を安定化させるはたらきを持つ
外力項
\begin{equation}
f_{i}
\end{equation}
外部からの力を表す項
外部からの力がない場合は0となる
数値流体力学の基礎方程式は以下の2つ
- 連続の式
- Navier-Stokes方程式
流れ場の変数は速度3成分(\(U_{i}\))と圧力(\(p\))の4つ
直接数値シミュレーション(DNS)
前節で説明した2つの支配方程式を,何の手も加えずそのまま解く手法が直接数値シミュレーション(Direct Numerical Simulation:DNS)である
誰にでもわかるシンプルな手法で,原点にして頂点な計算手法だが,以下のようなメリット・デメリットがある
- 十分な格子解像度と数値精度で適切な初期条件と境界条件を設定すれば,文字通り「すべての乱流現象」を計算できる
- 格子より小さい渦の影響が極めて小さくなるくらいの格子解像度であれば,長い時間における統計的なデータとしては十分に信頼に値するものが得られる
- 非常に高い格子解像度を必要とするため,計算コストが天文学的
- そもそもDNSの計算に使えるような完璧な初期条件を用意することができない
- カオス理論によって,時々刻々の変化の精度を確保できない
格子解像度について
一切のモデル化を伴わずにNavier-Stokes方程式を解くためには,格子のサイズを流れ場に存在する最小スケールの渦と同程度にする必要がある
この「最小スケールの渦」がとにかく小さいため,現在の最高性能のスーパーコンピューターをもってしてもRe数の低い簡単な流れ場(チャネル乱流など)の計算を行うので精いっぱいである
実際にどのくらいの計算コストが必要なのか,鳥人間コンテストに出てくるような人力飛行機(速度\(U\),代表長さ\(L\))で計算してみる
定常飛行をしている機体を考えると,機体による乱れエネルギーの供給(翼や胴体によって空気が乱されること)と空気の粘性による乱れエネルギーの散逸(最小スケールまで分裂した渦が最終的に熱エネルギーに変換されること)は同程度だと考えられる
機体による単位時間当たりの乱れエネルギーの供給\(\varepsilon ~[\mathrm{m^2/s^3}]\)はエネルギー\(U^{2} ~[\mathrm{m^2/s^2}]\)を時間\(L/U ~[\mathrm{s}]\)で割ることによって求められる
\begin{equation}
\varepsilon=\mathcal{O}\left[\frac{U^{3}}{L}\right]
\end{equation}
一方,空気の粘性による単位時間当たりの乱れエネルギーの散逸\(\varepsilon ~[\mathrm{m^2/s^3}]\)は,動粘性係数\(\nu ~[\mathrm{m^2/s}]\)と渦の最小スケール\(\eta ~[\mathrm{m}]\)を用いて次元解析的に求められる
\begin{equation}
\varepsilon=\mathcal{O}\left[\frac{\nu^{3}}{\eta^{4}}\right]
\end{equation}
供給と散逸が等しいとすると,代表長さ\(L\)と渦の最小スケール\(\eta\)の関係が導かれる
\begin{equation}
\frac{L}{\eta}=\mathcal{O}[Re^{3/4}]
\end{equation}
高Re数の流れ場では,乱れが供給される代表長さに比べて乱れが散逸するスケールは非常に小さく,その比はおおむねRe数の3/4乗に比例することがわかる
一般的な人力飛行機では,Re数は\(10^{5}\)程度,代表長さ(主翼のコード長)は\(1 ~[\mathrm{m}]\)程度なので,人力飛行機まわりの流れに存在する最小スケールの渦(乱れ)は次のように求まる
\begin{equation}
\eta=\mathcal{O}\left[\frac{L}{Re^{3/4}}\right]=\mathcal{O}\left[\frac{1 ~[\mathrm{m}]}{\left(10^{5}\right)^{3/4}}\right]=\mathcal{O}\left[10^{-4} ~[\mathrm{m}]\right]
\simeq0.1 ~[\mathrm{mm}]
\end{equation}
人力飛行機まわりの流れをDNSで計算するためには,格子サイズを最低でも0.1 [mm]以下にする必要があり,全長10 [m],全幅30 [m],全高5 [m]の計算領域を確保した場合,格子点数は\(1.5\times 10^{15}\)にも及ぶ
プログラムをかじったことがある人なら,1000兆×1000兆の連立一次方程式を数万回解く必要があるプログラムの大変さが理解できると思う
ちなみにこれまで実施された最大規模の計算は,2004年に行われた分割数\(1.74\times 10^{11}\)の平行平板間乱流(チャネル乱流)である
≫https://doi.org/10.1016/j.ijheatfluidflow.2004.02.010
旅客機のRe数が\(10^{8}\)程度であることを考えると,DNSの実用がまだまだ先であることが実感できる
初期条件について
仮に上記の計算コストを支払えるだけの圧倒的技術力と財力があったとしても,DNSの計算を行うための初期条件の用意が非常に難しい
例えばDNSを使って将来の天気を正確に予測するプログラムを作るとする
そのためには,同時刻における,全世界のありとあらゆる場所の,ありとあらゆるスケールの速度,圧力,温度などの情報を,寸分の狂いなく正確に測定する必要がある
少し考えただけでも困難なことがわかる
カオス理論について
超高性能のスーパーコンピューターと,全知全能の神によって初期条件を設定できたとしても,DNSの計算は難しい
数値計算を行うと,離散化に伴う誤差や,計算を行うことによる丸め誤差が必ず生じる
1回に生じる誤差は極めて小さいものでも,それが積もり積もって非常に大きな結果の違いが生まれることになる
この現象はバタフライ効果やカオス理論として知られ,三重振り子の計算などで確認することができる
≫バタフライ効果 - Wikipedia
≫カオス理論 - Wikipedia
先日のカオス振り子動画を見て極端な場合を試してみたくなったので、3重振り子で高精度物理演算してみた。初期の振り子の角度を10の100乗(グーゴル)分の1ずつだけずらしたものを100個同時に再生。完全に一致してるように見えるけど、1分20秒くらいから「それ」がやってくる。 pic.twitter.com/a7E2OASIDe
— So Takamoto (@tkmtSo) May 25, 2017
このような事情から,現状DNSは基礎研究にしか用いられておらず,工学の現場で設計などに使用できるようになるにはまだまだ時間がかかると考えられている
Navier-Stokes方程式をそのまま計算する手法としてDNSがある
計算コストなどの面から実用には程遠い
フィルターをかけた基礎方程式
DNSのように流れ場に存在するすべての乱れを直接解こうとすると莫大な計算コストがかかってしまうことから,流れ場にある種の平均操作(フィルター)を施して,乱れを「直接解く乱れ」と「モデル化して解く乱れ」に分類する手法が編み出された
フィルター操作によって,速度\(\mathbf{u}\)と圧力\(p\)は平均値と変動量に分けられる(レイノルズ分解)
\begin{align}
u_{i}&=\overline{u}_{i}+u'_{i} \\
p&=\overline{p}+p'
\end{align}
バーで表された平均値は格子上で直接求められ,プライムで表された変動量はモデル化することによって求められる
連続の式とNavier-Stoke方程式に上記のフィルター操作を施すと,フィルターをかけた連続の式
\begin{equation}
\nabla\cdot\mathbf{\overline{u}}=0
\end{equation}
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\tag{3}
\end{equation}
およびフィルターをかけたNavier-Stokes方程式が得られる(外力項は省略している)
\begin{equation}
\frac{\partial \mathbf{\overline{u}}}{\partial t}
+\nabla\cdot\left(\mathbf{\overline{u}~\overline{u}}\right)
=
-\frac{\nabla \overline{p}}{\rho}
+\nabla\cdot\left[\nu\left\{\nabla\mathbf{\overline{u}}+\left(\nabla\mathbf{\overline{u}}\right)^{\mathrm{T}}\right\}-\boldsymbol{\tau}\right]
\end{equation}
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\tag{4}
\end{equation}
ここで,\(\boldsymbol{\tau}=\tau_{ij}\)はフィルター操作によって表された変動速度の2次の相間項で,フィルターから漏れた変動量による影響を表す項である
\begin{equation}
\boldsymbol{\tau}=\overline{\mathbf{uu}}-\overline{\mathbf{u}}~\overline{\mathbf{u}}
\end{equation}
\begin{equation}
\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}
\end{equation}
\(\tau_{ij}\)は未知数であり,分子粘性応力\(\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\)と同じ次元を持つことから,レイノルズ応力(RANS)やSGS応力(LES)とよばれる
フィルター操作に関して,以下の仮定をおく
\begin{equation}
\overline{\frac{\partial f}{\partial x}}=\frac{\partial \overline{f}}{\partial x}, \quad
\overline{\frac{\partial f}{\partial t}}=\frac{\partial \overline{f}}{\partial t}
\end{equation}
本来フィルター操作は空間的にも時間的にも変化しうるものなので,この仮定は厳密には正しくない
もちろんこの過程に起因する誤差も生じる可能性があるが,現状はあまり重要視されていない
連続の式
これを踏まえたうえで,連続の式にフィルター操作を施すと次のようになる
\begin{align}
\overline{\frac{\partial u_{i}}{\partial x_{i}}}=0
\quad \longleftrightarrow \quad
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\end{align}
Navier-Stokes方程式
フィルターをかけたNavie-Stokes方程式は次のようになる
\begin{align}
\overline{\frac{\partial u_{i}}{\partial t}}
+\overline{\frac{\partial \left( u_{i}u_{j} \right)}{\partial x_{j}}}
=
-\frac{1}{\rho}\overline{\frac{\partial p}{\partial x_{i}}}
+\overline{\frac{\partial}{\partial x_{j}}\left\{ \nu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)\right\} }
\end{align}
\begin{align}
\longleftrightarrow \quad
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u_{i}u_{j}}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{align}
ここで,両辺から\(\frac{\partial \left(\overline{u_{i}u_{j}}\right)}{\partial x_{j}}\)を引いて\(\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}\)を足すと
\begin{align}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}- \frac{\partial \left(\overline{u_{i}u_{j}}\right)}{\partial x_{j}}+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
\end{align}
右辺の\(\frac{\partial}{\partial x_{j}}\)について整理して
\begin{align}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)
-\left(\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}\right)\right\}
\end{align}
よって
\begin{equation}
\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}
\end{equation}
とすると,フィルターをかけたNavier-Stokes方程式が導かれる
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\end{equation}
フィルターをかけたことにより新たな変数\(\tau_{ij}\)が追加され,方程式4つにたいして変数が5つ(\(\overline{u}_{i}\),\(\overline{p}\),\(\tau_{ij}\))になってしまった
これら5つの変数を求める(方程式を閉じる)ためには,\(\overline{u}_{i}\)と\(\overline{p}\)からなる\(\tau_{ij}\)の方程式を追加する必要があり,ここで\(\tau_{ij}\)を求めるために導入されるモデル化された方程式が俗にいう「乱流モデル」とよばれるものである
直接計算の計算コストを下げるために基礎方程式に平均操作(フィルター)を施す
フィルター操作によって,乱れの効果を表す項\(\tau_{ij}\)が基礎方程式に表される
新たな変数\(\tau_{ij}\)を表すモデル式を追加することで基礎方程式は完結する
モデル式にはさまざまな形式があり,「乱流モデル」とよばれる
乱流モデル(DNS/LES/RANS)の概要
前節で説明したある種の平均操作として,レイノルズ平均(時間平均であることが多い)を用いるとRANS(Reynolds-Averaged-Navier-Stokes Eq.),空間平均(隣接する全てのセルの平均値など)を用いるとLES(Large Eddy Simulation)と呼ばれる手法になる
RANS,LES,DNSの特徴を以下にまとめる
| RANS | LES | DNS | |
| フィルター | レイノルズ平均 | 空間平均 | なし |
| 計算の次元 | 2次元 or 3次元 | 3次元 | 3次元 |
| 定常/非定常 | 主に定常計算 | 非定常計算 | 非定常計算 |
| \(\tau_{ij}\) | レイノルズ応力 | SGS応力 | なし |
| モデルする乱れ | ほぼすべてのスケール | 格子幅以下のスケール | なし |
| 計算コスト | 低い(1~10) | 高い(100) | 非常に高い(1000~) |
| 実用性 | 産業界で広く普及 | 実用化までもう少し | 基礎研究レべル |
| 特徴 | 簡単な流れ場で高い精度 | 複雑な流れ場に対応可能 | ほぼ正しい |
| 精度 | モデルの種類に依存 | 格子の精度に依存 | 計算手法に依存 |
RANSとLESには,それぞれいろいろな特徴を持ったモデルが存在するので,流れ場の性質や計算コストに見合ったものを選定する必要がある
DNS,LES,RANSの違いを,旅行の思い出を残すための媒体で例えてみる
- 流れ場のすべてを完璧に把握するためにDNSで計算を行いたい
- DNSは計算コストが高すぎて実用には程遠い
- 計算コストを下げるために,空間平均フィルターをかけて格子解像度を落とした計算(LES)を行う
- LESなら複雑乱流場に対しても高い精度で計算できるし,3次元の非定常計算が可能である
- LESの計算コストもまだまだ高く,まだ実用するには難しい
- さらに計算コストを下げるために,時間平均フィルターをかけた定常計算(RANS)を行う
- RANSでは流れ場の非定常的な運動はわからないが,CFDの利用においては平均的な流れ場の特性(航空機の巡航時の揚力など)さえわかれば十分なことが多い
- 旅行の思い出を余すところなく完璧に残すために,プロが使う4Kテレビ対応カメラと超高音質マイクを使いたい
- 実際にはそんな高い機材を購入することはできないし,機材を運搬したりカメラマンを雇ったりすることはできない
- 負担を下げるために,画質を落としてスマホでHD動画を撮ることにする
- 画質を落としたとはいえ十分に高画質なHDであるし,動画で思い出を残すことができる
- だがスマホの動画を旅行中ずっと回しておくのも疲れるし,スマホの充電がなくなってしまう
- さらに負担を下げるために,スマホで旅行の写真を撮ることにする
- 細かな動きや雰囲気が伝わらないとはいえ,写真でも十分に旅行の思い出を振り返ることができる
わかりやすい?
フィルター操作の種類によって,乱流モデルはRANSとLESに大別される
RANSは流れ場のほぼすべてのスケールの乱れをモデル化する低コストな乱流モデル,LESは格子幅以下のスケールの乱れをモデル化する高精度な乱流モデルである
それぞれの特徴を把握して,流れ場の特性と利用可能なコストをもとに乱流モデルを選択する必要がある
まとめ
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(1)に関連して,流れの基礎方程式と基礎方程式のモデル化の概要について説明した
流れの基礎方程式は連続の式とNavier-Stokes方程式
Navier-Stokes方程式を直接計算するDNS,空間平均で乱れをモデル化して高精度で計算するLES,時間平均で乱れをモデル化して低コストで計算するRANSという手法がある
次の記事ではそれぞれの乱流モデルについて詳しい説明を行っていく
RANSについての詳しい説明はこちら
LESについての詳しい説明はこちら
↓まとめ記事
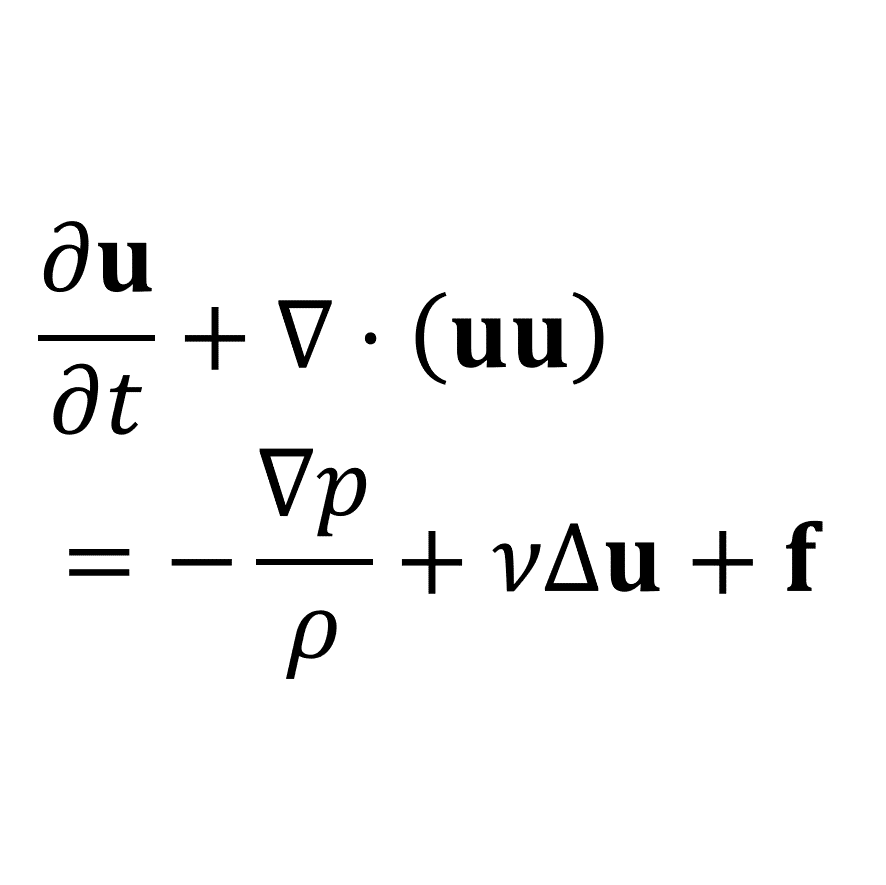

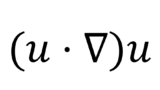
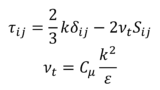
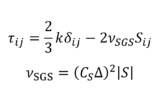

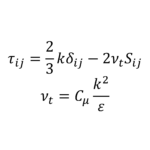

コメント