RANSについて,研究でCFDを使うことになった大学院生の役に立つような説明を行う
keyword: レイノルズ平均モデル,応力方程式モデル,渦粘性モデル,0方程式モデル,1方程式モデル,2方程式モデル,Baldwin-Lomaxモデル,Spalart-Allmarasモデル,標準k-εモデル,低Re数型RANSモデル,非線形RANSモデル
はじめに
この記事の内容は以下の前提に基づいている
- 非圧縮性流体の乱流流れ
- 密度\(\rho\),粘性係数\(\mu\)は一定
- 熱移動はなし
- CFDを研究で使う大学院生に必要な知識に重点を置く(ググって得られる知識と専門書の中間くらい)
参考文献はこちら
数値流体力学で必須のテンソル解析についての知識はこちら
流れの数値シミュレーションの概要
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(1)に関連して,モデル化の手法の1つであるRANSについて説明する
前回の記事
RANSの概要
RANSは,その計算コストの低さと取り扱いの容易さから,産業界で広く普及しているモデルである
RANS,LES,DNSの特徴をまとめたものは次のようになる
| RANS | LES | DNS | |
| フィルター | レイノルズ平均 | 空間平均 | なし |
| 計算の次元 | 2次元 or 3次元 | 3次元 | 3次元 |
| 定常/非定常 | 主に定常計算 | 非定常計算 | 非定常計算 |
| \(\tau_{ij}\) | レイノルズ応力 | SGS応力 | なし |
| モデルする乱れ | ほぼすべてのスケール | 格子幅以下のスケール | なし |
| 計算コスト | 低い(1~10) | 高い(100) | 非常に高い(1000~) |
| 実用性 | 産業界で広く普及 | 実用化までもう少し | 基礎研究レべル |
| 特徴 | 簡単な流れ場で高い精度 | 複雑な流れ場に対応可能 | ほぼ正しい |
| 精度 | モデルの種類に依存 | 格子の精度に依存 | 計算手法に依存 |
RANSは流れ場のほぼすべての乱れをモデル化するため,モデルごとに得意な流れと苦手な流れが存在する
そのような特徴から,既存のモデルの欠点を補う形で多くの派生形がこれまでに生まれてきた
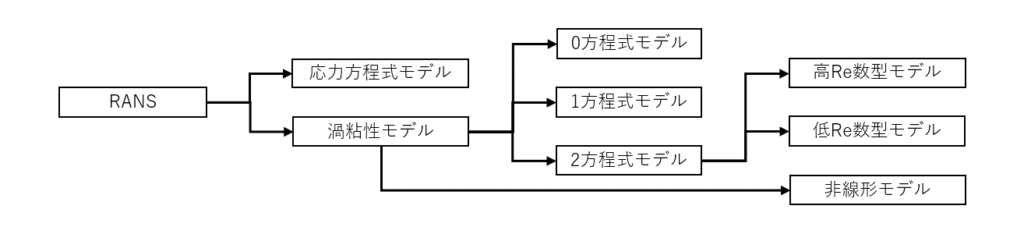
今回の記事では,それぞれのモデルの考え方や特徴,使い方などを説明していく
RANSの基礎方程式
Filtered Navier-Stokes方程式
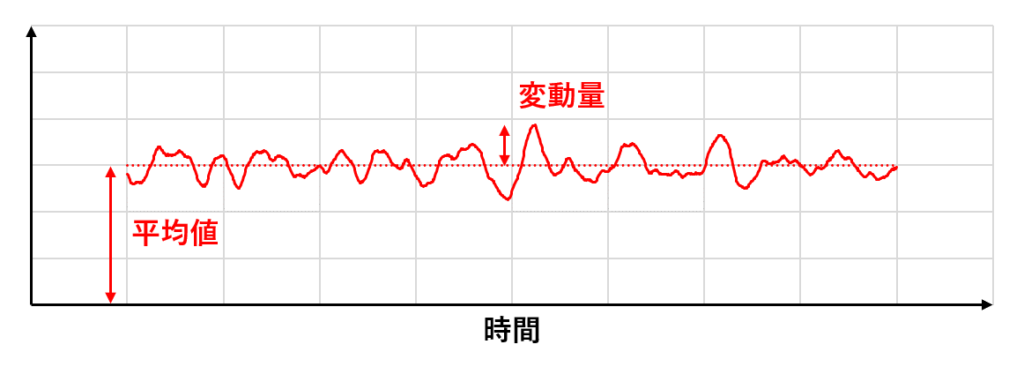
数値流体力学では,フィルター操作によって速度\(u_{i}\)と圧力\(p\)が平均値と変動量に分けられる
\begin{align}
u_{i}&=\overline{u}_{i}+u'_{i} \\
p&=\overline{p}+p'
\end{align}
また,フィルターをかけた支配方程式は次のように表される
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\end{equation}
ここで,乱流の効果を表す未知数であるレイノルズ応力\(\tau_{ij}\)は次の式で表される
\begin{equation}
\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}
\end{equation}
ここまでが前回の記事の内容である
レイノルズ平均(Reynolds Average)
RANSで用いられる平均操作はレイノルズ平均とよばれるものである
レイノルズ平均は以下のような特徴をもつアンサンブル平均である
\begin{align}
\overline{\overline{u_{i}}}=\overline{u_{i}}
\end{align}
\begin{align}
\overline{\overline{u}_{i}\overline{u}_{j}}=\overline{u}_{i}\overline{u}_{j}
\end{align}
\begin{align}
\overline{u'}_{i}=0
\end{align}
\begin{align}
\overline{u'_{i}\overline{u}_{j}}= \overline{\overline{u}_{i}u'_{j}}=0
\end{align}
これらの特徴を用いてレイノルズ応力\(\tau_{ij}\)を計算すると次のようになる
\begin{equation}
\tau_{ij}=\overline{u'_{i}u'_{j}}
\end{equation}
\(\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}\) に \(u_{i}=\overline{u}_{i}+u'_{i}\) を代入して
\begin{align}
\tau_{ij}
&=\overline{(\overline{u}_{i}+u'_{i}) (\overline{u}_{j}+u'_{j})}
-\overline{(\overline{u}_{i}+u'_{i})}~\overline{ (\overline{u}_{j}+u'_{j})} \\
&=\overline{(\overline{u}_{i}\overline{u}_{j}+\overline{u}_{i}u'_{j}+u'_{i}\overline{u}_{j}+u'_{i}u'_{j})}-( \overline{\overline{u}}_{i}+\overline{u'}_{i})(\overline{\overline{u}}_{j}+\overline{u'}_{j}) \\
&=\overline{\overline{u}_{i}\overline{u}_{j}}
+\overline{u'_{i}\overline{u}_{j}}+\overline{\overline{u}_{i}u'_{j}}
+\overline{u'_{i}u'_{j}}-\overline{\overline{u_{i}}}~\overline{\overline{u_{j}}}\\
&=\overline{u'_{i}u'_{j}}
\end{align}
Reynolds-Averaged Navier-Stokes 方程式
以上より,RANSの基礎方程式は次のようになる
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\overline{u'_{i}u'_{j}}\right\}
\tag{1}
\end{equation}
これらの式にレイノルズ応力\(\tau_{ij}=\overline{u'_{i}u'_{j}}\)を与えるモデル式を追加することで,流れ場の速度や圧力を計算することができるようになる
レイノルズ応力を与えるモデルは大きく分けて「応力方程式モデル」と「渦粘性モデル」があるので,次節以降ではそれらのモデルについて説明していく
CFDの説明で「RANSは時間平均したNavier-Stokes方程式を解いて定常計算を行う」とされることがあるが,この説明は厳密には間違っており,RANSでも非定常計算は不可能ではない
このことを理解するために,アンサンブル平均(レイノルズ平均)と時間平均の定義を確認してみる
アンサンブル平均と時間平均
アンサンブル平均とは,N個のサンプルの平均であり,次の式で定義される
\begin{equation}
\overline{u}=\frac{1}{N}\sum_{N} u
\end{equation}
時間平均とは,ある時間Tにおける平均であり,次の式で定義される
\begin{equation}
\overline{u}=\frac{1}{T}\int_{t}^{t+T}u\:dt
\end{equation}
2つの平均は一見違うものに見えるかもしれないが,時間平均は「ある時間Tの中から抜き出した異なるNt個の時刻に対するアンサンブル平均」と言い換えることができる
\begin{equation}
\overline{u}=\frac{1}{N_{t}}\sum_{N_{t}} u(t)
\end{equation}
つまり,時間平均はアンサンブル平均の一種であり,アンサンブル平均はより一般的な平均の概念ということである
RANSにおける定常計算
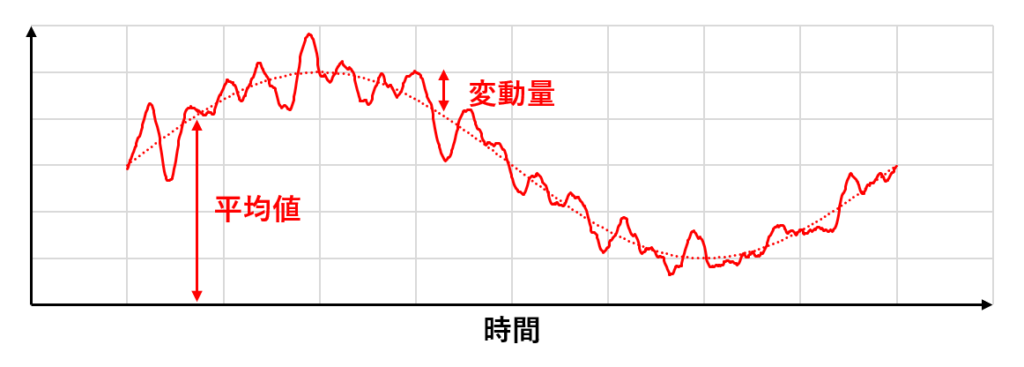
定常的な乱流は下の図のようになる(縦軸は速度や圧力などの物理量)
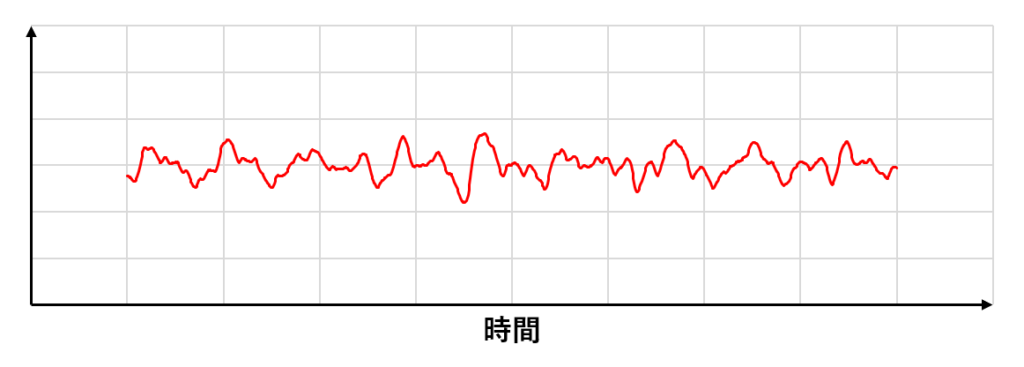
時間平均をとると図の点線の定常流になり,レイノルズ分解によって平均値と変動量に分けられる
時間平均よりも一般的な概念であるアンサンブル平均の考え方をするならば,下の図のようになる
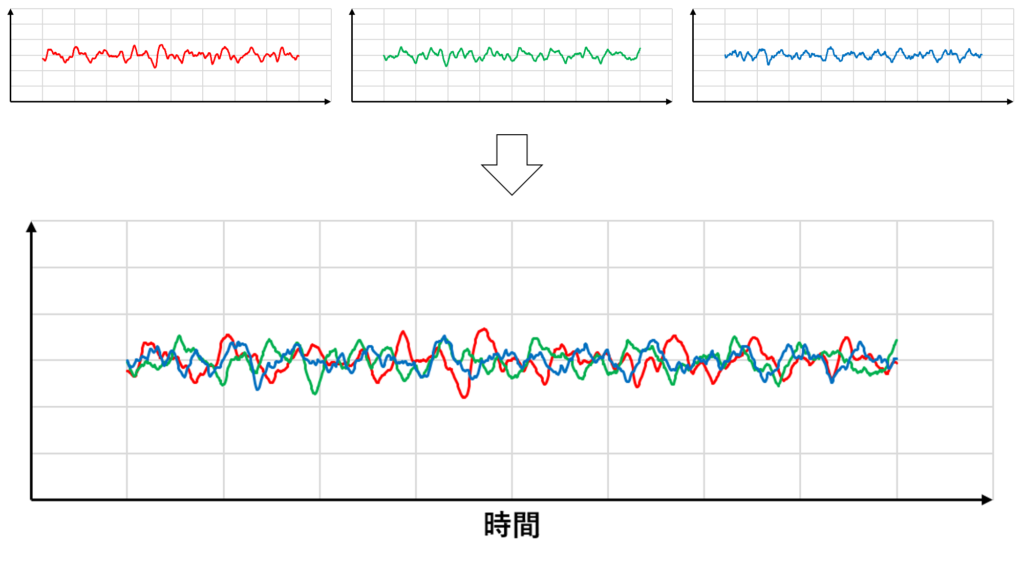
サンプル数を十分に大きくすればアンサンブル平均は時間平均の直線に限りなく近づいていくはずなので,定常流ではアンサンブル平均と時間平均は同じものであるということがわかる
RANSにおける非定常計算
非定常的な乱流は下の図のようになる(おおきなsinカーブが流れ場の非定常性で小さな乱れが乱流によるもの)
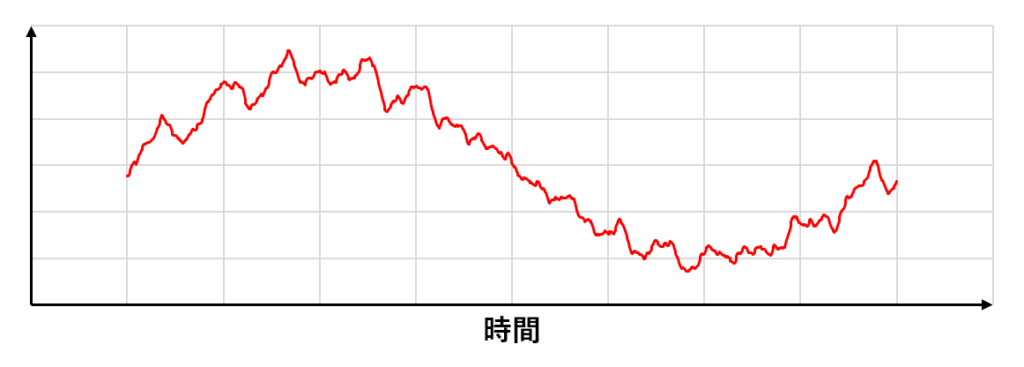
時間平均の考え方だとこのような非定常流れは計算できないように感じるが,より一般的な概念であるアンサンブル平均を用いると次のように考えることができる
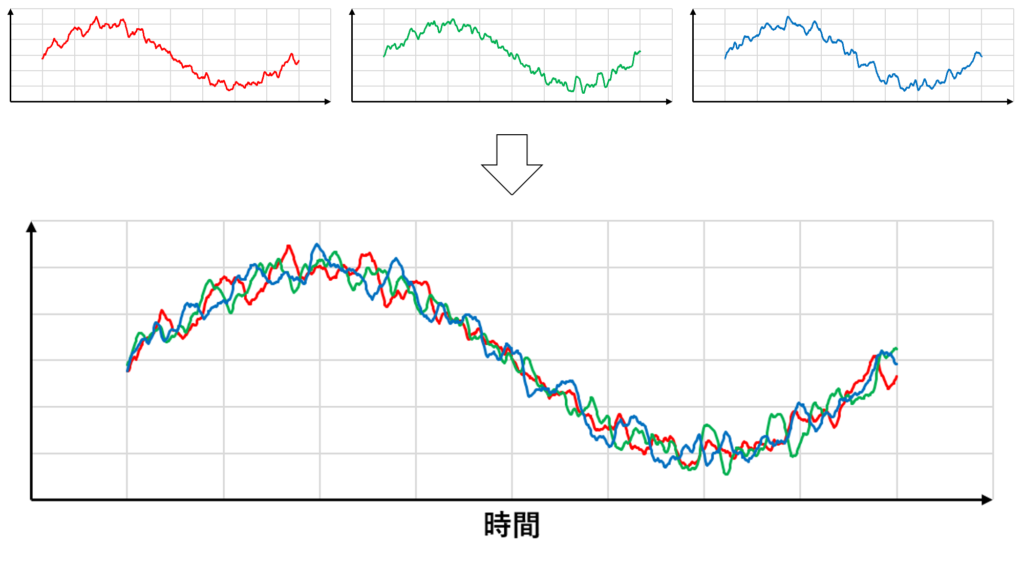
このように,アンサンブル平均を使えば非定常流れでも平均値と変動量を考えることができるため,RANSでも非定常計算が不可能ではないことが理解できる
実際,Re数が低い円柱まわりの流れをRANSで計算すると,円柱の背後に非定常的な渦(カルマン渦)が現れることが確認されている
≫パッと知りたい! 人と差がつく乱流と乱流モデル講座 第13回 13.1 円柱周り流れ解析、13.2 LESの計算結果、13.3 RANSとの比較
非定常RANSの注意点
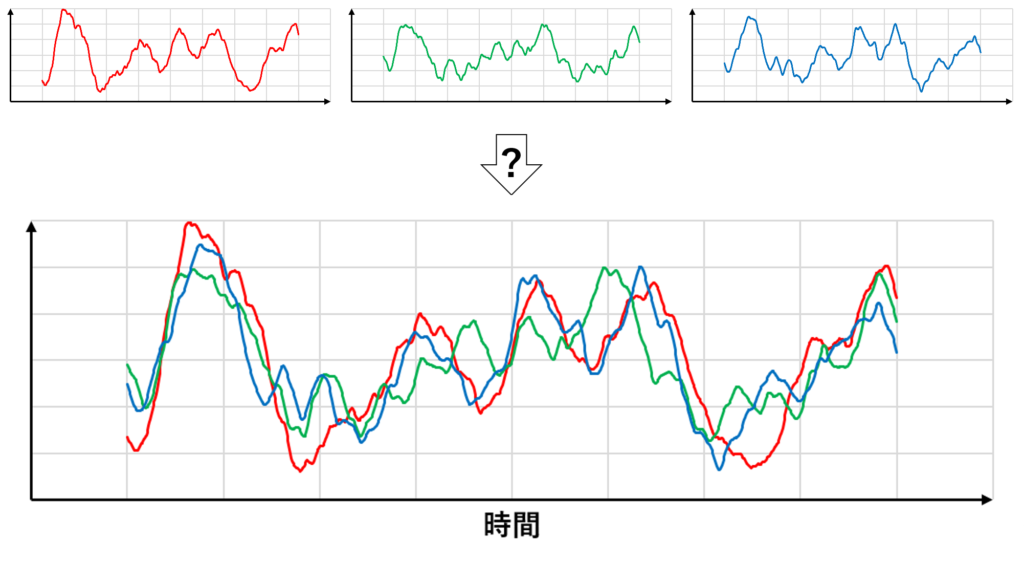
ただし,非定常RANSを計算するためには流れ場の非定常性と乱れのスケールがしっかりと分離している必要がある
下の図のように,流れ場の非定常性と乱れのスケールが近い場合はアンサンブル平均をとったとしても流れ場の非定常性をうまく把握することができない
アンサンブル平均とは,N個のサンプルの平均である
時間平均は,N個のサンプルを「異なる時刻における流れ場」としたアンサンブル平均である
定常な流れ場ではアンサンブル平均と時間平均は一致する
RANSでも非定常計算を行うことはできなくはないが,乱れのタイムスケールと非定常性のタイムスケールが分離されている必要がある
ここまで長々と説明してきたが,実際非定常計算をRANSでやることはあまりないと思うので,RANS=時間平均という理解でもあまり問題はない
ただ,論文や学会発表などで「RANSは時間平均をとって定常計算を行う手法です」と言ってしまうと思わぬところから横やりが来るかもしれないので注意が必要である
応力方程式モデル
概要
応力方程式モデルは,レイノルズ応力\(\tau_{ij}\)を直接求める輸送方程式をモデル化する手法であり,以下のような特徴を持つ
- 工学的応用にとって重要な多くの流れに対して,渦粘性モデルに対する優位性を示している
- 個々のケースに対してモデルの選択や定数の調整をしなくてもよい結果を出すことができる
- モデルが複雑になり方程式が増えるため,渦粘性モデルと比べて計算コストが高い
- モデルの各部分の検証が十分でなく,完成度が低い
- レイノルズ応力のすべての項に対して初期条件や境界条件を設定する必要があり,煩雑である
- レイノルズ応力方程式は拡散的ではなく,数値的不安定になりやすい
メリットに比べてデメリットが大きく,応力方程式モデルはあまり使われていない
モデル化手法
レイノルズ応力の輸送方程式は次の式で表される
\begin{equation}
\frac{\partial \tau_{ij}}{\partial t}
+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
=P_{ij}+\Pi_{ij}-\varepsilon_{ij}+\frac{\partial J_{ijk}}{\partial x_{k}}
\end{equation}
ここで,\(\Pi_{ij}\),\(\varepsilon_{ij}\),\(J_{ijk}\)は\(\overline{u}_{i}\),\(\overline{p}\),\(\tau_{ij}\)を使って表すことができない項なので,それぞれモデル化を行う必要がある
レイノルズ応力は対称テンソルなので独立な成分は6つであり,\(\varepsilon_{ij}\)については輸送方程式を解いて求める必要があるので,合計で7つの方程式を解くことで\(\tau_{ij}\)を求めることができる
レイノルズ応力方程式を省略せずに書くと次の式である
\begin{align}
\frac{\partial \tau_{ij}}{\partial t}
+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
&=
-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}} \\
&\quad+\frac{\partial }{\partial x_{k}}\left\{
-\overline{u'_{i}u'_{j}u'_{k}}
-\frac{1}{\rho}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\nu\frac{\partial \tau_{ij}}{\partial x_{k}}
\right\}
\end{align}
実質微分項
\begin{equation}
\frac{\partial \tau_{ij}}{\partial t}+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
\end{equation}
第1項\(\frac{\partial \tau_{ij}}{\partial t}\)が時間項,第2項 \(\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}\)が移流項であり,左辺全体でレイノルズ応力\(\tau_{ij}\)の実質微分を表している
生成項
\begin{equation}
P_{ij}=-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
\end{equation}
平均速度勾配による\(\tau_{ij}\)の生成項である
この項をモデル化せずに扱えるのが応力方程式モデルの最大のメリットである
圧力-ひずみ相間項
\begin{equation}
\Pi_{ij}=\overline{\frac{p'}{\rho}\left(\frac{\partial u'_{i}}{\partial x_{j}}+\frac{\partial u'_{j}}{\partial x_{i}}\right)}
\end{equation}
レイノルズ応力間の再配分を行う役割を持つ項で,この項のモデル化が応力方程式モデルで最も重要となる
散逸項
\begin{equation}
\varepsilon_{ij}=2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{equation}
散逸については,\(\varepsilon_{ij}=\frac{2}{3}\delta_{ij}\varepsilon\)として,\(\varepsilon\)の輸送方程式を解くことによって求められる
拡散項
\begin{equation}
J_{ijk}=J_{(T)ijk}+J_{(P)ijk}+J_{(V)ijk}
\end{equation}
\begin{align}
J_{(T)ijk}&=-\overline{u'_{i}u'_{j}u'_{k}} \\
J_{(P)ijk}&=-\frac{1}{\rho}\left(\overline{p'u'_{i}}\delta_{jk}+\overline{p'u'_{j}}\delta_{ik}\right) \\
J_{(V)ijk}&=\nu\frac{\partial \tau_{ij}}{\partial x_{k}}
\end{align}
\(J_{(T)ijk}\),\(J_{(P)ijk}\),\(J_{(V)ijk}\)はそれぞれ速度変動,圧力変動,粘性による拡散流束を表している
レイノルズ応力の輸送方程式は,まず変動速度\(u'_{i}\)についての連続の式とNavier-Stoke方程式を求め,\(\frac{\partial \tau_{ij}}{\partial t}\)を計算することで求めることができる
連続の式とNavier-Stokes方程式は次の式で表される
(連続の式)
\begin{equation}
\frac{\partial u_{k}}{\partial x_{k}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}
+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\end{equation}
これに\(u_{i}=\overline{u}_{i}+u'_{i}\)を代入する
(連続の式)
\begin{equation}
\frac{\partial}{\partial x_{k}}\left(\overline{u}_{k}+u'_{k}\right)=0
\end{equation}
(Navier-Stokes方程式)
\begin{align}
&\frac{\partial}{\partial t}\left(\overline{u}_{i}+u'_{i}\right)
+\frac{\partial}{\partial x_{j}}\left(\overline{u}_{i}\overline{u}_{j}+u'_{i}\overline{u}_{j}+\overline{u}_{i}u'_{j}+u'_{i}u'_{j}\right)
= \\
&-\frac{1}{\rho}\frac{\partial}{\partial x_{i}}\left(\overline{p}+p'\right)
+\frac{\partial}{\partial x_{j}}\left[\nu\left\{\frac{\partial}{\partial x_{j}}\left(\overline{u}_{i}+u'_{i}\right)+\frac{\partial}{\partial x_{i}} \left(\overline{u}_{j}+u'_{j}\right) \right\}\right]
\tag{i}
\end{align}
また,レイノルズ平均を施した連続の式とNavier-Stokes方程式は次の式になる
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{k}}{\partial x_{k}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\tag{ii}
\end{equation}
2つの式の差(i)-(ii)をとることによって,変動速度\(u'_{i}\)に対する連続の式とNavier-Stokes方程式が求まる
(連続の式)
\begin{equation}
\frac{\partial u'_{k}}{\partial x_{k}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{align}
\frac{\partial u'_{i}}{\partial t}
+\frac{\partial}{\partial x_{j}}
\left(u'_{i}\overline{u}_{j}+\overline{u}_{i}u'_{j}+u'_{i}u'_{j}\right)
=
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial u'_{i}}{\partial x_{j}}+\frac{\partial u'_{j}}{\partial x_{i}}\right)+\tau_{ij}\right\}
\end{align}
整理して
\begin{align}
&\frac{\partial u'_{i}}{\partial t}
+\frac{\partial \left(u'_{i}\overline{u}_{j}\right)}{\partial x_{j}}
= \\
&-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{-u'_{i}u'_{j}-\overline{u}_{i}u'_{j}+\nu\left(\frac{\partial u'_{i}}{\partial x_{j}}+\frac{\partial u'_{j}}{\partial x_{i}}\right)+\tau_{ij}\right\} \\
\tag{iii}
\end{align}
(iii)を用いて,レイノルズ応力\(\tau_{ij}\)の輸送方程式を求めていく
ただし,次のことを常に意識しておく
- 積の微分 \((fg)'=f'g+fg'\)
- アンサンブル平均の性質 \(\overline{\overline{f}g'}=\overline{f}\:\overline{g'}\),\(\overline{f'\overline{g}}=\overline{f'}\:\overline{g}\)
- 変動速度の連続の式 \(\frac{\partial u_{k}}{\partial x_{k}}=0\)
\(\tau_{ij}\)の時間微分は次の式で表される
\begin{equation}
\frac{\partial \tau_{ij}}{\partial t}=\frac{\partial \overline{u'_{i}u'_{j}}}{\partial t}
=\overline{\frac{\partial u'_{i}}{\partial t}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial t}} \\
\tag{iv}
\end{equation}
\(\frac{\partial u'_{i}}{\partial t}\)は(iii)において\(j \rightarrow k\)とし,\(\frac{\partial u'_{j}}{\partial t}\)は(iii)において\(i \rightarrow j\),\(j \rightarrow k\)とすることで次のようになる
\begin{align}
\frac{\partial u'_{i}}{\partial t}
&=
-\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}} \\
&\quad+\frac{\partial}{\partial x_{k}}\left\{-u'_{i}u'_{k}-\overline{u}_{i}u'_{k}+\nu\left(\frac{\partial u'_{i}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{i}}\right)+\tau_{ik}\right\} \\
\frac{\partial u'_{j}}{\partial t}
&=
-\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}} \\
&\quad+\frac{\partial}{\partial x_{k}}\left\{-u'_{j}u'_{k}-\overline{u}_{j}u'_{k}+\nu\left(\frac{\partial u'_{j}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{j}}\right)+\tau_{jk}\right\}
\tag{v}
\end{align}
(iv)の最右辺の\(\frac{\partial u'_{i}}{\partial t}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial t}\)に(v)を代入する
\begin{align}
&\frac{\partial u'_{i}}{\partial t}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial t}\\
&=u'_{j}\left[-\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}
+\frac{\partial}{\partial x_{k}}\left\{-u'_{i}u'_{k}-\overline{u}_{i}u'_{k}+\nu\left(\frac{\partial u'_{i}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{i}}\right)+\tau_{ik}\right\}\right] \\
&\quad+u'_{i}\left[-\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}}
+\frac{\partial}{\partial x_{k}}\left\{-u'_{j}u'_{k}-\overline{u}_{j}u'_{k}+\nu\left(\frac{\partial u'_{j}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{j}}\right)+\tau_{jk}\right\}\right] \\
&=\left(-u'_{j}\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}} \right)
+\left(-u'_{j}\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}-u'_{i}\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}}\right) \\
&\quad+\left(-u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}u'_{k}}{\partial x_{k}}\right)
+\left(-u'_{j}\frac{\partial \overline{u}_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial \overline{u}_{j}u'_{k}}{\partial x_{k}}\right) \\
&\quad+\left(u'_{j}\frac{\partial \tau_{ik}}{\partial x_{k}}+u'_{i}\frac{\partial \tau_{jk}}{\partial x_{k}}\right) \\
&\quad+\left(\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right)
+\left(\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{i}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{j}}\right)
\tag{vi}
\end{align}
(vi)の右辺の各項をそれぞれ計算し,レイノルズ平均を行う
(右辺第1項)
\begin{align}
&-u'_{j}\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}} \\
&=-u'_{j}\left(\frac{\partial u'_{i}}{\partial x_{k}}\overline{u}_{k}+u'_{i}\frac{\partial \overline{u}_{k}}{\partial x_{k}}\right)-u'_{i}\left(\frac{\partial u'_{j}}{\partial x_{k}}\overline{u}_{k}+u'_{j}\frac{\partial \overline{u}_{k}}{\partial x_{k}}\right)
=-\overline{u}_{k}\left(\frac{\partial u'_{i}}{\partial x_{k}}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}\right) \\
&=-\overline{u}_{k}\frac{\partial u'_{i}u'_{j}}{\partial x_{k}} \\
&\longrightarrow \overline{-\overline{u}_{k}\frac{\partial u'_{i}u'_{j}}{\partial x_{k}}}
=-\overline{u}_{k}\frac{\partial \overline{u'_{i}u'_{j}}}{\partial x_{k}}
=-\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
\end{align}
(右辺第2項)
\begin{align}
&-u'_{j}\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}-u'_{i}\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}} \\
&=-\frac{1}{\rho}\left\{\left(u'_{j}\frac{\partial p'}{\partial x_{i}}+\frac{\partial u_{j}}{\partial x_{i}}p'\right)-\frac{\partial u_{j}}{\partial x_{i}}p'\right\}
-\frac{1}{\rho}\left\{\left(u'_{i}\frac{\partial p'}{\partial x_{j}}+\frac{\partial u_{i}}{\partial x_{j}}p'\right)-\frac{\partial u_{i}}{\partial x_{j}}p'\right\} \\
&=-\frac{1}{\rho}\left(\frac{\partial p'u'_{j}}{\partial x_{i}}-\frac{\partial u_{j}}{\partial x_{i}}p'\right)-\frac{1}{\rho}\left(\frac{\partial p'u'_{i}}{\partial x_{j}}-\frac{\partial u_{i}}{\partial x_{j}}p'\right) \\
&=-\frac{1}{\rho}\left(\frac{\partial p'u'_{j}}{\partial x_{i}}+\frac{\partial p'u'_{i}}{\partial x_{j}}\right)
+\frac{p'}{\rho}\left(\frac{\partial u_{j}}{\partial x_{i}}+\frac{\partial u_{i}}{\partial x_{j}}\right) \\
&=-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(p'u'_{j}\delta_{ik}+p'u'_{i}\delta_{jk}\right)
+\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right) \\
&\longrightarrow \overline{-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(p'u'_{j}\delta_{ik}+p'u'_{i}\delta_{jk}\right)
+\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)} \\
&\qquad=-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
\end{align}
ただし,クロネッカーのデルタを使った超絶技巧を用いている
\begin{equation}
\frac{\partial}{\partial x_{k}}\delta_{ik}
=\left\{\begin{array}{cl}
\frac{\partial}{\partial x_{i}} & (i=k) \\
0 & (i \neq k) \end{array}\right.
\end{equation}
(右辺第3項)
\begin{align}
&-u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}u'_{k}}{\partial x_{k}} \\
&=-u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}-u'_{i}\left(\frac{\partial u'_{j}}{\partial x_{k}}u'_{k}+u'_{j}\frac{\partial u'_{k}}{\partial x_{k}}\right)
=-\left(u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}+\frac{\partial u'_{j}}{\partial x_{k}}u'_{i}u'_{k}\right)
=-\frac{\partial u'_{i}u'_{j}u'_{k}}{\partial x_{k}} \\
&\longrightarrow -\overline{\frac{\partial u'_{i}u'_{j}u'_{k}}{\partial x_{k}}}
=-\frac{\partial \overline{u'_{i}u'_{j}u'_{k}}}{\partial x_{k}}
\end{align}
(右辺第4項)
\begin{align}
&-u'_{j}\frac{\partial \overline{u}_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial \overline{u}_{j}u'_{k}}{\partial x_{k}} \\
&=-u'_{j}\left(\frac{\partial \overline{u}_{i}}{\partial x_{k}}u'_{k}+\overline{u}_{i}\frac{\partial u'_{k}}{\partial x_{k}}\right)
-u'_{i}\left(\frac{\partial \overline{u}_{j}}{\partial x_{k}}u'_{k}+\overline{u}_{j}\frac{\partial u'_{k}}{\partial x_{k}}\right)
=-u'_{j}u'_{k}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-u'_{i}u'_{k}\frac{\partial \overline{u}_{j}}{\partial x_{k}} \\
&\longrightarrow \overline{-u'_{j}u'_{k}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-u'_{i}u'_{k}\frac{\partial \overline{u}_{j}}{\partial x_{k}}}
=-\overline{u'_{j}u'_{k}}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\overline{u'_{i}u'_{k}}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
=-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
\end{align}
(右辺第5項)
\begin{align}
&u'_{j}\frac{\partial \tau_{ik}}{\partial x_{k}}+u'_{i}\frac{\partial \tau_{jk}}{\partial x_{k}} \\
&=u'_{j}\frac{\partial \overline{u'_{i}u'_{k}}}{\partial x_{k}}+u'_{i}\frac{\partial \overline{u'_{j}u'_{k}}}{\partial x_{k}} \\
&\longrightarrow \overline{u'_{j}\frac{\partial \overline{u'_{i}u'_{k}}}{\partial x_{k}}+u'_{i}\frac{\partial \overline{u'_{j}u'_{k}}}{\partial x_{k}}}
=\overline{u'}_{j}\frac{\partial \overline{u'_{i}u'_{k}}}{\partial x_{k}}+\overline{u'}_{i}\frac{\partial \overline{u'_{j}u'_{k}}}{\partial x_{k}}
=0
\end{align}
(右辺第6項)
\begin{align}
&\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}} \\
&=\nu \left\{\left(\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}+u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}\right)-\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}\right\} \\
&\quad+\nu \left\{\left(\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}+u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right)-\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right\} \\
&=\nu\left\{\frac{\partial}{\partial x_{k}}\left(u'_{j}\frac{\partial u'_{i}}{\partial x_{k}}\right)-\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}\right\}
+\nu\left\{\frac{\partial}{\partial x_{k}}\left(u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}\right)-\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right\} \\
&=\nu\frac{\partial}{\partial x_{k}}\left(\frac{\partial u'_{i}}{\partial x_{k}}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}\right)
-2\nu\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}
=\nu\frac{\partial}{\partial x_{k}}\left(\frac{\partial u'_{i}u'_{j}}{\partial x_{k}}\right)
-2\nu\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}} \\
&\longrightarrow \overline{\nu\frac{\partial}{\partial x_{k}}\left(\frac{\partial u'_{i}u'_{j}}{\partial x_{k}}\right)
-2\nu\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
=\frac{\partial}{\partial x_{k}}\left(\nu\frac{\partial \tau_{ij}}{\partial x_{k}}\right)
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{align}
(右辺第7項)
\begin{align}
\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{i}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{j}}
=\nu u'_{j}\frac{\partial}{\partial x_{i}}\frac{\partial u'_{k}}{\partial x_{k}}+\nu u'_{i}\frac{\partial}{\partial x_{j}}\frac{\partial u'_{k}}{\partial x_{k}}
=0
\end{align}
よって,\(\tau_{ij}\)の時間微分\(\frac{\partial \tau_{ij}}{\partial t}\)は次のようになる
\begin{align}
\frac{\partial \tau_{ij}}{\partial t}
&=-\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
-\frac{\partial \overline{u'_{i}u'_{j}u'_{k}}}{\partial x_{k}} \\
&\quad -\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
+\frac{\partial}{\partial x_{k}}\left(\nu\frac{\partial \tau_{ij}}{\partial x_{k}}\right)
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{align}
両辺整理すると,レイノルズ応力方程式が得られる
\begin{align}
\frac{\partial \tau_{ij}}{\partial t}
+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
&=
-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}} \\
&\quad+\frac{\partial }{\partial x_{k}}\left\{
-\overline{u'_{i}u'_{j}u'_{k}}
-\frac{1}{\rho}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\nu\frac{\partial \tau_{ij}}{\partial x_{k}}
\right\}
\end{align}
応力方程式モデルは,モデル化したレイノルズ応力の輸送方程式を解くことによって直接\(\tau_{ij}\)を求める計算手法である
渦粘性モデルよりも複雑な流れ場に対して優位性を持っているが,計算コストが高く(7つの方程式を解く必要がある),条件設定の煩雑さや数値計算が不安定になりやすいなどの問題からあまり使われていない
渦粘性モデル
RANSにおけるもう1つの手法である渦粘性モデルについて説明する
概要
分子粘性応力が粘性係数と速度勾配の積で与えられるのと同様に,レイノルズ応力も乱れによる拡散を表す係数と平均速度勾配の積で与えらえると仮定すると,次のようになる
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}-\nu_{t}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)
=\frac{2}{3}k\delta_{ij}-2\nu_{t}S_{ij}
\tag{1}
\end{equation}
ここで,\(k=\frac{1}{2}\tau_{ii}=\frac{1}{2}\overline{u'_{i}u'_{j}}\) は乱流エネルギーであり,\(S_{ij}=\frac{1}{2}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\) はひずみ速度テンソルである
乱れによる拡散を表す係数\(\nu_{t}\)は分子粘性係数と対比して渦粘性係数とよばれ,単位は \(\mathrm{[m^{2}/s]}\) である
このようにレイノルズ応力を渦粘性係数と平均速度勾配との積で表すモデルを渦粘性モデルといい,1877年にブシネスクによって提唱されたことからブシネスク近似ともいう
メリットとデメリットは以下の通り
- もともと6つの成分を持っていたレイノルズ応力テンソル\(\tau_{ij}\)が,渦粘性係数\(\nu_{t}\)という1つのスカラーに集約されたことで,モデルの計算コストが大幅に削減される
- 渦粘性モデルは簡単な流れ場ではよい近似となるが,工学の現場で用いられるような複雑な流れ場においては成立しないことが多い
複雑な流れ場に対する精度は完璧とは言えないが,後述するk-εモデルを代表として優れたモデルが多く存在しており,産業界で最も使われているモデルである
渦粘性モデルの右辺第1項\(\frac{2}{3}k\delta_{ij}\)は,両辺の縮約をとったときに必要になる項である
\begin{equation}
\tau_{ii}=\frac{2}{3}k\delta_{ii}-\nu\left(\frac{\partial u_{i}}{\partial x_{i}}+\frac{\partial u_{i}}{\partial x_{i}}\right)
=\frac{2}{3}3\left(\frac{1}{2}\tau_{ii}\right)-0=\tau_{ii}
\end{equation}
\begin{align}
\left(\delta_{ii}=\delta_{11}+\delta_{22}+\delta_{33}=3 , \qquad
\frac{\partial u_{i}}{\partial x_{i}}=0\right)
\end{align}
もしくは,渦粘性モデルは「レイノルズ応力の非等方成分(偏差テンソル)が渦粘性係数と速度勾配の積に等しいと仮定した」と考えることもできる
\begin{equation}
\tau_{ij}^{a}=\tau_{ij}-\frac{1}{3}\tau_{kk}=\tau_{ij}-\frac{2}{3}\left(\frac{1}{2}\tau_{kk}\delta_{ij}\right)=\tau_{ij}-\frac{2}{3}k\delta_{ij}=-\nu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
\end{equation}
モデル化手法
渦粘性モデルの式をReynolds-Averaged Navier-Stokes方程式に代入すると次のようになる
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数は\(\nu_{t}\)ただ1つであり,この\(\nu_{t}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
ただし,レイノルズ応力の非等方成分\(\frac{2}{3}\rho k\)が圧力項に組み込まれているため,平均圧力\(\overline{p}\)を求める際は注意が必要である
渦粘性モデルはレイノルズ応力を渦粘性係数と速度勾配の積で近似するモデルである
変数が渦粘性係数1つだけになり,応力方程式モデルに比べて計算コストが低い
渦粘性近似は簡単な流れ場に対してはいい近似である
渦粘性モデルは,\(\nu_{t}\)を求めるために追加する方程式の数で,0方程式モデル,1方程式モデル,2方程式モデルに分類される
0方程式モデルから順番に説明していく
0方程式モデル(混合長理論)
0方程式モデルのもっとも簡単なモデルとして,Plandtlが提案した混合長理論がある
混合長理論では,小さな流体の塊が運動量を保持したままで移動できる距離を表す混合長\(l_{m}\)を用いて渦粘性係数を次のように表す
\begin{equation}
\nu_{t}=l_{m}^{2}\left|\frac{d\overline{u}}{dy}\right|
\end{equation}
一般的な乱流境界層では\(l_{m}=\kappa y\)とすることで対数速度分布が得られ,実験結果と良い一致を示すことがわかっている
混合長\(l_{m}\)を与えることで,新たな方程式を一切加えることなく計算を行うことができるシンプルなモデルではあるが,カギを握る混合長\(l_{m}\)を与えるには実験結果などの経験的要素が必須となるため普遍的なモデルにはなりえない
航空分野では, 翼周りの流れに対して有効なBaldwin-Lomaxモデルという0方程式モデルが広く使用されてきた
Baldwin-Lomaxモデルでは,流れ場の領域を内層(添え字\(_{I}\))と外層(添え字\(_{O}\))に分割し,渦粘性係数を次の式で与える
\begin{equation}
\nu_{t}=\left\{\begin{array}{ll}
\nu_{t_{I}} & \left(\nu_{t_{I}}<\nu_{t_{O}}\right) \\
\nu_{t_{O}} & \left(\nu_{t_{I}}>\nu_{t_{O}}\right)
\end{array}\right.
\end{equation}
内層の渦粘性係数\(\nu_{t_{I}}\)は,特性長さ\(l_{I}\)と平均渦度テンソルの大きさ\(\left|\boldsymbol{\overline{\Omega}}\right|\)を用いていて次の式で表される
\begin{equation}
\nu_{t_{I}}=\frac{1}{\sqrt{2}}l_{I}^{2}\left|\boldsymbol{\overline{\Omega}}\right|
\end{equation}
ここで,平均渦度テンソル\(\overline{\mathbf{\Omega}}\)は
\begin{equation}
\overline{\mathbf{\Omega}}=\overline{\Omega}_{ij}
=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial u_{j}}{\partial x_{i}}\right), \qquad
\left|\boldsymbol{\overline{\Omega}}\right|
=\sqrt{\overline{\Omega}_{ij}\overline{\Omega}_{ij}}
\end{equation}
混合長\(l_{I}\)は,壁面からの距離\(d\),摩擦速度\(u_{\tau}=\sqrt{\nu_{e}|\frac{\partial u}{\partial y}|}\),壁面での動粘性係数\(\nu_{w}\)を用いて次の式で表される
\begin{equation}
l_{i}=\kappa y\left\{1-\exp{\left(-\frac{y^{+}}{A_{VD}}\right)}\right\}, \qquad
y^{+}=\frac{u_{\tau}d}{\nu_{w}}
\end{equation}
\begin{equation}
\kappa=0.41, \qquad A_{VD}=26
\end{equation}
外層では,
\begin{align}
F
=\frac{1}{\sqrt{2}}\frac{l_{I}}{\kappa}\left|\boldsymbol{\overline{\Omega}}\right|
=\frac{1}{2}y\left(1-\exp{\left\{-\frac{y^{+}}{A_{VD}}\right)}\right\}\left|\boldsymbol{\overline{\Omega}}\right|
\simeq \frac{1}{2}y\left|\boldsymbol{\overline{\Omega}}\right|
\end{align}
を用いて,\(F_{max}\)と\(y_{max}\)を次のように定義する
\begin{equation}
F_{max}=\mathrm{max}(F), \qquad F(y_{max})=F_{max}
\end{equation}
ここから,\(\overline{u}_{Diff}=\overline{u}_{max}-\overline{u}_{min}\)を用いて
\begin{equation}
F_{O_{1}}=y_{max}F_{max}\mathrm{min}\left(1,C_{O_{1}}\left(\frac{\overline{u}_{Diff}}{F_{max}}\right)^{2}\right)
\end{equation}
\begin{equation}
F_{O_{2}}=\left\{1+C_{O_{21}}\left(C_{O_{22}}\frac{y}{y_max}\right)^{6}\right\}^{-1}
\end{equation}
を導入し,外層の渦粘性係数\(\nu_{t_{O}}\)を次の式で計算する
\begin{equation}
\nu_{t_{O}}=\alpha C_{O_{3}}F_{O_{1}}F_{O_{2}}
\end{equation}
ここで,定数群は以下で与えられる
\begin{align}
\alpha=0.0168, \quad C_{O_{1}}=0.25, \quad C_{O_{21}}=5.5, \quad C_{O_{22}}=0.3, \quad C_{O_{3}}=1.6
\end{align}
翼周りの流れ場は,翼付近の乱れが非常に大きい領域と翼から離れた乱れが非常に小さい領域という性質の大きく異なる2つの領域をもった外部流れである
そのような流れ場に対しては,内層と外層で流れ場を分割してそれぞれの渦粘性係数を設定するというBaldwin-Lomaxモデルの考え方が有効になる
参考
≫宇宙航空研究開発機構研究開発報告 - 航空工学におけるレイノルズ平均乱流モデルの概観と 時間スケールによる物理的意味の考察
混合長モデルは,渦粘性係数を混合長の2乗と速度勾配の積で表すモデルである
追加の方程式が必要のない最も低コストなモデルだが,経験的な定数を設定する必要がある
普遍的なモデルにはなりえないが,Baldwin-Lomaxモデルのように特定の分野に特化した優れたモデルもある
1方程式モデル(S-Aモデル)
1方程式モデルにはいくつか種類があるが,この記事では航空分野で多く利用されているSpalart-Allmaras(S-A)モデルについて説明する
Spalart-Allmarasモデルは,渦粘性係数の輸送方程式を解くことによって渦粘性係数を計算するモデルである
このモデルにおいて,渦粘性係数は次の式で与えられる
\begin{equation}
\nu_{t}=\tilde{\nu}\frac{\left(\tilde{\nu}/\nu\right)^{3}}{\left(\tilde{\nu}/\nu\right)^{3}+C_{V}^{3}}
\end{equation}
\(\tilde{\nu}\)は次の輸送方程式によって求められる
\begin{equation}
\frac{\partial \tilde{\nu}}{\partial t}
+\left(\mathbf{\overline{u}}\cdot\nabla\right)\tilde{\nu}
=
C_{p}\tilde{\nu}\tilde{S}
-C_{\varepsilon_{1}}f_{\varepsilon}\left(\frac{\tilde{\nu}}{d}\right)^{2}
+\frac{1}{\sigma}\left[
\nabla\cdot\left\{\left(\tilde{\nu}+\nu\right)\nabla\tilde{\nu}\right\}
+C_{D}\left(\nabla\tilde{\nu}\right)^{2}
\right]
\end{equation}
Spalart-Allmarasモデルを構成する定数群や関係式は経験的な仮定を多く含んでいるため汎用的なモデルにはなりえないものの,航空分野のモデルとしては高度にチューニングされており,適切に運用すれば低い計算コストで高い予測性能が期待できるモデルである
基本表現
\(\tilde{\nu}\)の輸送方程式
\begin{equation}
\frac{\partial \tilde{\nu}}{\partial t}
+\overline{u}_{i}\frac{\partial \tilde{\nu}}{\partial x_{i}}
=
C_{p}\tilde{\nu}\tilde{S}
-C_{\varepsilon_{1}}f_{\varepsilon}\left(\frac{\tilde{\nu}}{d}\right)^{2}
+\frac{1}{\sigma}\left\{\frac{\partial}{\partial x_{j}}
\left(\tilde{\nu}+\nu\right)\frac{\partial \tilde{\nu}}{\partial x_{j}}
+C_{D}\frac{\partial \tilde{\nu}}{\partial x_{j}}\frac{\partial \tilde{\nu}}{\partial x_{j}}\right\}
\end{equation}
において,\(d\)は壁面からの距離であり,\(\tilde{S}\)および\(f_{\varepsilon}\)は次の式で与えられる
\begin{equation}
\tilde{S}=\frac{1}{\sqrt{2}}\left|\overline{\mathbf{\Omega}}\right|
+\frac{\nu}{\left(\kappa d\right)^{2}}f_{p}, \qquad
f_{\varepsilon}=g\left(\frac{1+C_{\varepsilon_{2}}^{6}}{g^{6}+C_{\varepsilon_{2}}^{6}}\right)^{1/6}
\end{equation}
ここで
\begin{equation}
f_{p}=\frac{\left(\tilde{\nu}/ u\right)^{3}-C_{V}^{3}\left(\tilde{\nu}/ \nu\right)+C_{V}^{3}}{\left(\tilde{\nu}/ \nu\right)^{4}+\left(\tilde{\nu}/ \nu\right)^{3}+C_{V}^{3}}
\end{equation}
\begin{equation}
g=r+C_{\varepsilon_{3}}\left(r^{6}-r\right), \qquad
r=\frac{\tilde{\nu}}{\tilde{S}\left(\kappa d\right)^{2}}
\end{equation}
モデル定数は次の通り
\begin{align}
&\sigma=2/3, \quad
C_{V}=7.1, \quad
\kappa=0.41, \quad
C_{p}=0.13, \quad
C_{D}=0.62, \quad \\
&C_{\varepsilon_{1}}=\frac{C_{p}}{\kappa^{2}}+\frac{1+C_{D}}{\sigma}, \quad
C_{\varepsilon_{2}}=2, \quad
C_{\varepsilon_{3}}=0.3, \quad
\end{align}
曲率および回転に対する補正
翼周りの流れのように主流が曲面に沿うような流れでは,主流方向で乱れの特性が変化し,モデルの精度が大きく低下してしまう
また,系全体が回転するような流れ場で発生するコリオリ力もモデルの精度に悪影響を与える
その補正として,\(\tilde{\nu}\)の輸送方程式の生成項を次のように変更する
\begin{equation}
C_{p}\rightarrow C_{p}F_{CR}
\end{equation}
補正関数\(F_{CR}\)は次の式で定義される
\begin{equation}
F_{CR}=
\left(1+C_{CR_{1}}\right)
\frac{C_{CR_{0}}\tilde{r}_{1}}{1+\tilde{r}_{1}}
\left\{1-C_{CR_{3}}\arctan{\left(C_{CR_{2}}\tilde{r}_{2}\right)}\right\}
-C_{CR_{1}}
\end{equation}
\begin{equation}
\tilde{r}_{1}=\frac{\left|\overline{\mathbf{S}}\right|}{\left|\overline{\mathbf{\Omega}}\right|}
\end{equation}
\begin{equation}
\tilde{r}_{2}=\frac{1}{4}\frac{\overline{\Omega}_{ik}\overline{S}_{kj}}{D^{4}}
\left(\frac{\partial \overline{S}_{ij}}{\partial t}+\overline{u}_{j}\frac{\partial \overline{S}_{ij}}{\partial x_{j}}+\varepsilon_{imn}\omega_{F_{m}}\overline{S_{jn}}+\varepsilon_{jmn}\omega_{F_{m}}\overline{S}_{in}\right)
\end{equation}
\begin{equation}
D=\frac{1}{2}\sqrt{\overline{S}_{ij}\overline{S}_{ij}+\overline{\tilde{\Omega}}_{ij}\overline{\tilde{\Omega}}_{ij}}
\end{equation}
ここで,\(\omega_{F}\)は系の回転角速度であり,この系の渦度テンソル\(\Omega_{ij}\)は次のように変換される
\begin{equation}
\Omega_{ij}\rightarrow \tilde{\Omega}_{ij}=\Omega_{ij}+2\varepsilon_{ikj}\omega_{F_{k}}
\end{equation}
定数は次の通り
\begin{equation}
C_{CR_{0}}=2, \quad
C_{CR_{1}}=1.0, \quad
C_{CR_{2}}=12, \quad
C_{CR_{3}}=1
\end{equation}
レイノルズ応力の非線形性に対する補正
レイノルズ応力を渦粘性係数と速度勾配で線形近似する線形渦粘性モデルでは,矩形ダクト内の第二次第二種流れに代表されるような「主流に垂直な断面内に発生する速度成分が重要な流れ場」を適切に記述できない
航空機の解析では翼と胴体の結合部付近でこのような流れが生じるため,Spalart-Allmarasモデルではそれに対する補正も行っている
レイノルズ応力の線形渦粘性近似からのずれ\(N_{ij}\)は次の式で計算される
\begin{equation}
N_{ij}=\nu_{t}C_{S_{\omega}}\frac{\overline{S}_{ik}\overline{\Omega}_{kj}+\overline{\Omega}_{ik}\overline{S}_{kj}}{\sqrt{\overline{S}_{mn}\overline{S}_{mn}+\overline{\Omega}_{mn}\overline{\Omega}_{mn}}}, \qquad
C_{S_{\omega}}=0.6
\end{equation}
この\(N_{ij}\)を用いて,レイノルズ応力は次のように補正される
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}-2\nu S_{ij}+N_{ij}
\end{equation}
非線形渦粘性モデルについてはこの記事の下で詳しく説明している
参考
≫宇宙航空研究開発機構研究開発報告 - 航空工学におけるレイノルズ平均乱流モデルの概観と 時間スケールによる物理的意味の考察
Spalart-Allmarasモデルは,輸送方程式を解くことで渦粘性を直接計算するモデルである
経験的な仮定を含んでいるため普遍的なモデルではないが,航空分野においては正しい運用をすることで計算コストの低さと高い精度の両立が可能である
2方程式モデル(k-εモデル)
2方程式モデルにはたくさんの種類があるが,その中でも特に広く利用されているk-εモデルについて説明する
概要
k-εモデルでは乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)を用いて渦粘性係数\(\nu_{t}\)が計算され,新たに追加した2つの変数\(k\)と\(\varepsilon\)は,それぞれ輸送方程式を計算することによって求められる
メリットとデメリットは以下の通り
- 経験的に与えられるパラメータが少なく,定数群の推奨値が定着している
- 壁関数を使うことで壁面近傍の格子点数を節約でき,計算コストが抑えられる
- 渦粘性係数が常に正の値になるので,数値安定性が比較的良好である
- 平均流線がある程度まっすぐで,流れ方向に加減速の少ない流れ場しか計算できない(渦粘性モデル全般の欠点)
- 一般的な乱流境界層を仮定したモデルなので,それ以外の壁面境界条件(剥離流れなど)をうまく扱うことができない
工学・工業の分野で最も広く利用されているモデルであり,k-εモデルをベースとしたモデルも多数開発されていることから,RANSを代表するようなモデルであるといえる
基本表現
k-εモデルでは,渦粘性係数\(\nu_{t}\)を次のように計算する
\begin{equation}
\nu_{t}=C_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)を求めることで,渦粘性係数\(\nu_{t}\)を計算することができる
乱流エネルギー
乱流エネルギー\(k\)は次のように定義され
\begin{equation}
k=\frac{1}{2}\tau_{ii}=\frac{1}{2}\overline{u'_{i}u'_{j}}
\end{equation}
以下に示すモデル化された\(k\)の輸送方程式を解くことによってを求められる
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\varepsilon
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
右辺の第1項が生成項\(P_{k}\),第2項が散逸項,第3項が拡散項であり,生成項\(P_{k}\)は次の式で表される
\begin{align}
P_{k}=-\overline{u'_{i}u'_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}} =2\nu_{t}S_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
\end{align}
\(k\)の輸送方程式は,レイノルズ応力方程式の縮約をとって,両辺を1/2倍することによって導出することができる
(縮約をとって1/2倍したレイノルズ応力方程式)
\begin{equation}
\frac{1}{2}\left(\frac{\partial \tau_{ii}}{\partial t} +\overline{u}_{k}\frac{\partial \tau_{ii}}{\partial x_{k}}\right)
=\frac{1}{2}\left\{P_{ii}+\Pi_{ii}-\varepsilon_{ii}+\frac{\partial}{\partial x_{k}} \left(J_{(T)iik}+J_{(P)iik}+J_{(V)iik}\right)\right\}
\end{equation}
上記の計算を行うと,\(k\)の輸送方程式は以下のようになる
\begin{align}
\frac{\partial k}{\partial t}
+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}
-\varepsilon
+\frac{\partial}{\partial x_{j}}\left(J_{(T_{k})j}+J_{(P_{k})j}+J_{(V_{k})j}\right)
\end{align}
ここで,各項は次のように計算される
(生成項)
\begin{equation}
P_{k}=\frac{1}{2}P_{ii}=\frac{1}{2}\left(-\tau_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{k}}-\tau_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}\right)
=-\overline{u'_{i}u'_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
\end{equation}
レイノルズ応力と平均速度勾配によって乱れが生成されることを表している
ここで、以下の渦粘性モデルの定義式
\begin{equation}
\overline{u'_{i}u'_{j}}=\tau_{ij}=\frac{2}{3}k\delta_{ij}-\nu_{t}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)
=\frac{2}{3}k\delta_{ij}-2\nu_{t}S_{ij}
\tag{1}
\end{equation}
を代入すると
\begin{equation}
P_{k}=-\overline{u'_{i}u'_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
=-\left(\frac{2}{3}k\delta_{ij}-2\nu_{t}S_{ij}\right)\frac{\partial \overline{u}_{i}}{\partial x_{j}}
=2\nu_{t}S_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
\end{equation}
(連続の式より、\(\frac{2}{3}k\delta_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
=\frac{2}{3}k\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0\))
(圧力-ひずみ相間項)
\begin{equation}
\Pi_{k}=\frac{1}{2}\Pi_{ij}=\frac{1}{2}\overline{\frac{p'}{\rho}\left(\frac{\partial u'_{i}}{\partial x_{i}}+\frac{\partial u'_{i}}{\partial x_{i}}\right)}=0
\end{equation}
変動速度の連続の式より0となる
(散逸項)
\begin{equation}
\varepsilon=\frac{1}{2}\varepsilon_{ij}=\frac{1}{2}\left(2\nu\overline{\frac{\partial u'_{i}}{\partial x_{j}}\frac{\partial u'_{i}}{\partial x_{j}}}\right)
\end{equation}
(拡散項)
\begin{equation}
J_{(k)j}=J_{(T_{k})j}+J_{(P_{k})j}+J_{(V_{k})j}
\end{equation}
\begin{align}
J_{(T_{k})j}&=\frac{1}{2}J_{(T)iij}=-\frac{1}{2}\overline{u'_{i}u'_{i}u'_{j}} \\
J_{(P_{k})j}&=\frac{1}{2}J_{(P)iij}=-\frac{1}{2}\frac{1}{\rho}\left(\overline{p'u'_{i}}\delta_{ij}+\overline{p'u'_{i}}\delta_{ij}\right)
=-\frac{1}{\rho}\overline{p'u'_{i}}\delta_{ij} \\
J_{(V_{k})j}&=\frac{1}{2}J_{(V)iij}=\nu\frac{\partial}{\partial x_{j}}\left(\frac{1}{2}\tau_{ii}\right)=\nu\frac{\partial k}{\partial x_{j}}
\end{align}
\(J_{(T_{k})j}\),\(J_{(P_{k})j}\),\(J_{(V_{k})j}\)はそれぞれ速度変動,圧力変動,粘性による拡散流束を表している
モデル化
\(J_{(T_{k})j}\)と\(J_{(P_{k})j}\)についてはモデル化が必要であり,一般に次のような勾配拡散近似が行われる
\begin{equation}
J_{(T_{k})j}+J_{(P_{k})j}=\frac{\nu_{t}}{\sigma_{k}}\frac{\partial k}{\partial x_{j}}
\end{equation}
これにより,モデル化した輸送方程式が得られる
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=-\overline{u'_{i}u'_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
-\varepsilon
+\frac{\partial}{\partial x_{j}}\left\{\left(\nu+\frac{\nu_{t}}{\sigma_{k}}\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
乱流散逸率
乱流散逸率\(\varepsilon\)は次のように定義され
\begin{equation}
\varepsilon=\frac{1}{2}\varepsilon_{ii}
=\nu\overline{\frac{\partial u'_{i}}{\partial x_{j}}\frac{\partial u'_{i}}{\partial x_{j}}}
\end{equation}
以下に示すモデル化された\(\varepsilon\)の輸送方程式を解くことによってを求められる
\begin{equation}
\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \varepsilon}{\partial x_{j}}\right\}
\end{equation}
\(\varepsilon\)の輸送方程式は,\(\varepsilon\)の時間微分に\(x_{j}\)で偏微分した変動速度についてのNavier-Stokes方程式を代入することで計算できる
(\(\varepsilon\)の時間微分)
\begin{align}
\frac{\partial \varepsilon}{\partial t}
=\frac{\partial}{\partial t}\left(\nu\overline{\frac{\partial u'_{i}}{\partial x_{j}}\frac{\partial u'_{i}}{\partial x_{j}}}\right)
=\overline{2\nu\frac{\partial u'_{i}}{\partial x_{j}}\frac{\partial}{\partial t}\left(\frac{\partial u'_{i}}{\partial x_{j}}\right)}
=\overline{2\nu\frac{\partial u'_{i}}{\partial x_{j}}\frac{\partial}{\partial x_{j}}\left(\frac{\partial u'_{i}}{\partial t}\right)}
\end{align}
(\(x_{j}\)で偏微分した変動速度についてのNavier-Stokes方程式)
\begin{align}
\frac{\partial}{\partial x_{j}}\left(\frac{\partial u'_{i}}{\partial t}\right)
&=\frac{\partial}{\partial x_{j}}\left[
-\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}} \right. \\
&\left. \quad+\frac{\partial}{\partial x_{k}}\left\{-u'_{i}u'_{k}-\overline{u}_{i}u'_{k}+\nu\left(\frac{\partial u'_{i}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{i}}\right)+\tau_{ik}\right\} \right]
\end{align}
上記の計算を行うと\(\varepsilon\)の輸送方程式は以下のようになる(さすがに面倒なので導出は省略する)
\begin{align}
\frac{\partial \varepsilon}{\partial t}
+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}
=P_{\varepsilon}-\Phi_{\varepsilon}
+\frac{\partial}{\partial x_{j}}\left(J_{(\varepsilon)j}+J_{(P_{\varepsilon})j}+J_{(V_{\varepsilon})j}\right)
\end{align}
各項の物理的意味は明瞭ではないものの,DNSによってその挙動は明らかになってきている
(生成項)
\begin{equation}
P_{\varepsilon}
=-2\nu\left(
\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}+
\overline{\frac{\partial u'_{k}}{\partial x_{i}}\frac{\partial u'_{k}}{\partial x_{j}}}
\right)\frac{\partial u'_{j}}{\partial x_{i}}
-2\nu\overline{u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}}\frac{\partial^{2} u'_{j}}{\partial x_{i} \partial x_{k}}
-2\nu\overline{\frac{\partial u'_{j}}{\partial x_{i}}\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{equation}
第1項は平均速度勾配による生成だと解釈され,第2項の意味は明確ではなく,第3項は渦の伸張による生成だと考えられている
(消滅項)
\begin{equation}
\Phi_{\varepsilon}=2\nu^{2}\overline{\frac{\partial^{2} u'_{i}}{\partial x_{j} \partial x_{k}}\frac{\partial^{2} u'_{i}}{\partial x_{j} \partial x_{k}}}
\end{equation}
\(k\)の輸送方程式における\(\varepsilon\)の類推から,\(\varepsilon\)の消滅を表すと考えられている
(拡散項)
\begin{align}
J_{(T_{\varepsilon})j}
&=-\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}u'_{j}} \\
J_{(P_{\varepsilon})j}
&=-\frac{\nu}{\rho}\overline{\frac{\partial u'_{j}}{\partial x_{i}}\frac{\partial p'}{\partial x_{i}}} \\
J_{(V_{\varepsilon})j}
&=\nu\frac{\partial \varepsilon}{\partial x_{j}}
\end{align}
\(J_{(T_{\varepsilon})j}\),\(J_{(P_{\varepsilon})j}\),\(J_{(V_{\varepsilon})j}\)はそれぞれ速度変動,圧力変動,粘性による拡散流束を表している
モデル化
生成項と消滅項はまとめて次のようにモデル化される
\begin{equation}
P_{\varepsilon}-\Phi_{\varepsilon}=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}
\end{equation}
\(J_{(T_{\varepsilon})j}\)と\(J_{(P_{\varepsilon})j}\)については,\(k\)と同様に勾配拡散近似が行われる
\begin{equation}
J_{(T_{\varepsilon})j}+J_{(P_{\varepsilon})j}=\frac{\nu_{t}}{\sigma_{\varepsilon}}\frac{\partial k}{\partial x_{j}}
\end{equation}
これにより,モデル化した輸送方程式が得られる
\begin{equation}
\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \varepsilon}{\partial x_{j}}\right\}
\end{equation}
標準k-εモデル
まとめると,k-εモデルの中でも最も基本となる「標準k-εモデル」とよばれるモデルは,次のようにして粘性係数を計算している
\begin{equation}
\nu_{t}=C_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\varepsilon
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
\begin{equation}
\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \varepsilon}{\partial x_{j}}\right\}
\end{equation}
\begin{equation}
C_{\mu}=0.09, \quad \sigma_{k}=1.0, \quad \sigma_{\varepsilon}=1.3, \quad
C_{\varepsilon_{1}}=1.44, \quad C_{\varepsilon_{2}}=1.92
\end{equation}
ここに示した定数は,以下のことを仮定して決定されている
- 定常2次元せん断乱流の乱流境界層の対数領域である
- 一様等方乱流(乱れの移流,生成,拡散がない)である
上記の仮定を大きく逸脱するような複雑な流れに対しては,標準k-εモデルの精度は低下してしまう
標準k-εモデルの定数について,1つずつ説明していく
定常2次元せん断流
平行平板間乱流などのように,平均速度勾配テンソルの\(\frac{\partial \overline{u}}{\partial y}\)以外の成分がすべて0である流れ場のことである
壁面近くの平均速度分布は次のようになる
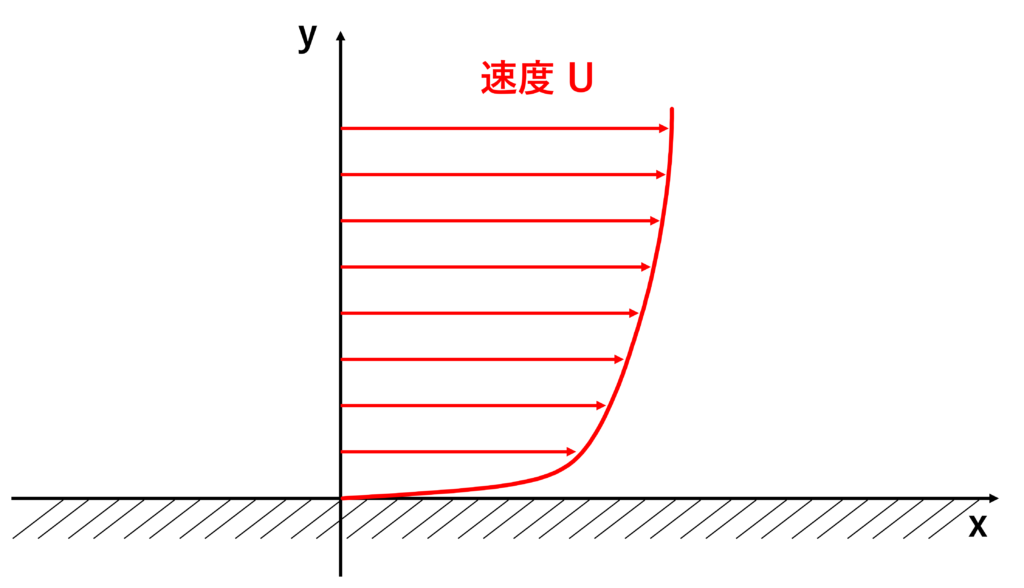
定常2次元せん断流では,せん断応力\(\tau\)は次の式で表される
\begin{equation}
\tau=\left(\mu+\mu_{t}\right)\frac{\partial u}{\partial y}
\end{equation}
壁面上では \(\nu_{t}=\mu_{t}/\rho=0\)なので,壁面せん断応力\(\tau_{w}\)は次のようになる
\begin{equation}
\tau_{w}=\mu\frac{\partial u}{\partial y}
\end{equation}
壁面せん断応力から摩擦速度\(u_{\tau}\)が定義され,主流速度\(\overline{u}\)および壁面からの距離\(y\)はそれぞれ次のように無次元化される
\begin{equation}
u_{\tau}=\sqrt{\frac{\tau_{w}}{\rho}}=\sqrt{\nu\frac{\partial u}{\partial y}}
\end{equation}
\begin{equation}
u^{+}=\frac{\overline{u}}{u_{\tau}}, \qquad y^{+}=\frac{u_{\tau}y}{\nu}
\end{equation}
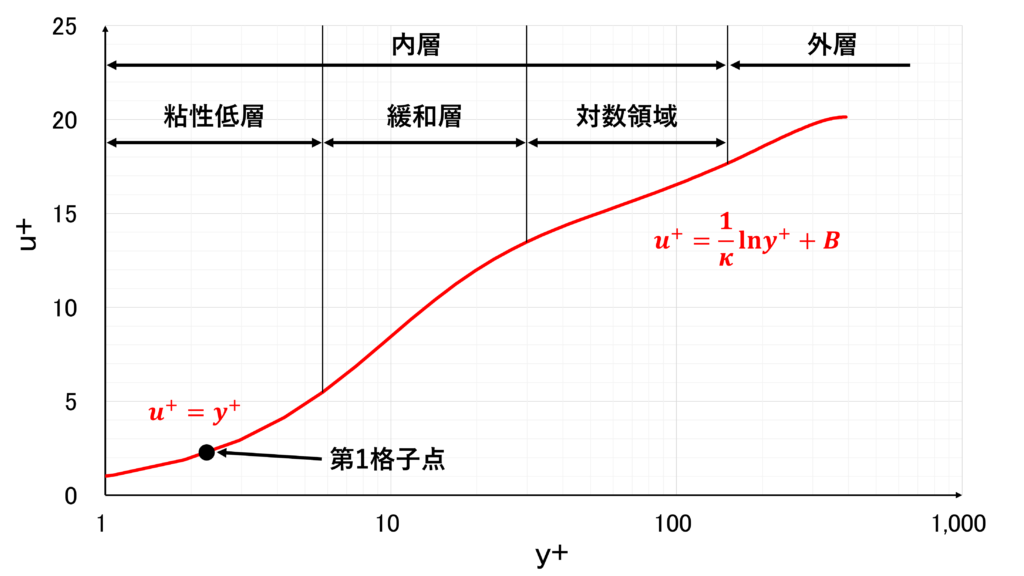
乱流境界層の速度分布
一般に,乱流境界層は壁面近くで壁からの影響を受ける内層と自由流近くの外層に分けられ,さらに内層は壁面ごく近くの分子粘性の影響が大きい領域である粘性低層,渦粘性の影響が大きい対数領域,それらの中間にある緩和層に分けられる
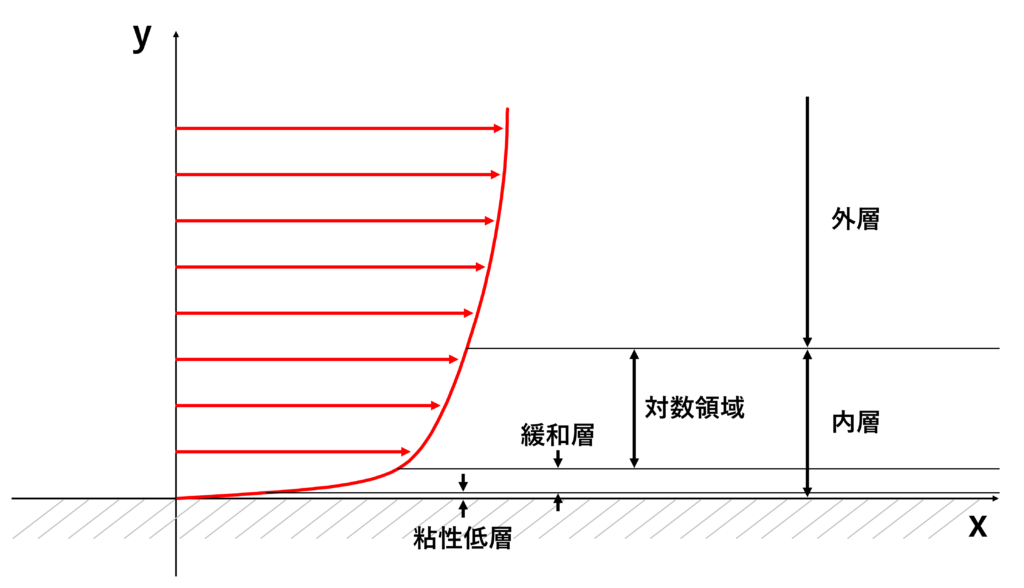
縦軸に無次元速度\(u^{+}\),横軸に無次元距離\(y^{+}\)の対数をプロットした片対数グラフは次のようになる
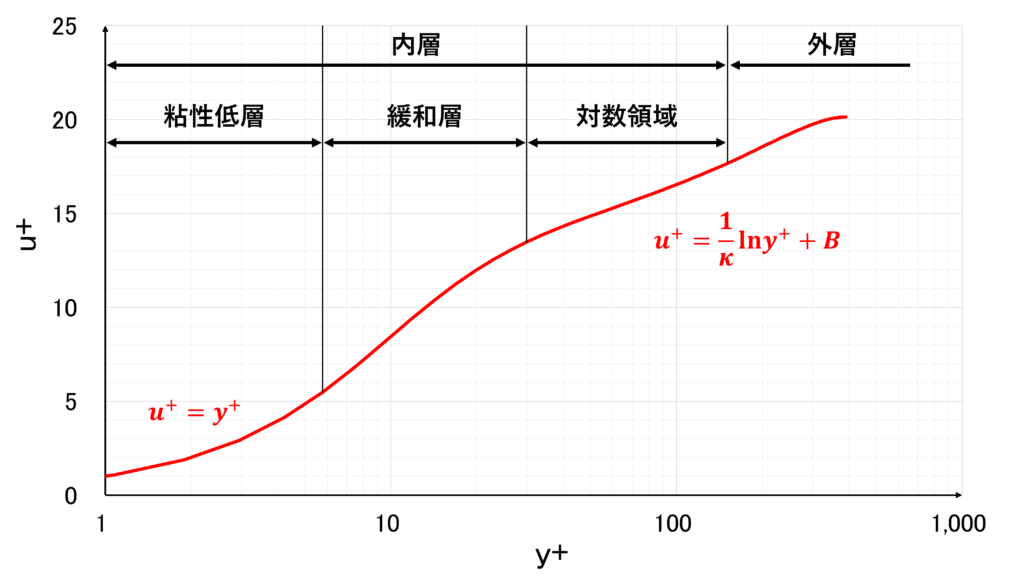
(粘性低層)
\(0 \leq y^{+} \leq 5\) であり,壁面の極近傍の領域である
壁面近くで乱れが減衰し,分子粘性が支配的になる(\(\nu \gg \nu_{t}\))
粘性低層では次のような層流の速度分布になる
\begin{equation}
u^{+}=y^{+}
\end{equation}
(緩和層)
\(5 \leq y^{+} \leq 30\) であり,粘性低層と対数領域の中間にある領域である
(対数領域)
\(30 \leq y^{+} \leq \delta_{t}^{+}\) であり,内層の一番外側にある領域である(\(\delta_{t}^{+}\)はレイノルズ数とともに大きくなる)
対数領域ではレイノルズ数が十分大きく分子粘性が無視できる(\(\nu \ll \nu_{t}\))ほか,乱れの生成と散逸の局所平衡が成立する
\begin{equation}
P_{k}=\varepsilon \qquad \left(P_{k}=-\overline{uv}\frac{\partial u}{\partial y}\right)
\end{equation}
速度分布は次のような対数速度分布になる
\begin{equation}
u^{+}=\frac{1}{\kappa}\ln{y^{+}}+B
\end{equation}
定数\(\kappa\)はカルマン定数とよばれ,乱流境界層では実験的に\(\kappa \simeq 0.4\),\(B \simeq 5\)とされている
また,対数領域では実験的に次の関係式が成り立つことがわかっている
\begin{equation}
\frac{|\overline{uv}|}{k}=0.3 \quad (=\sqrt{C_{\mu}})
\end{equation}
一様等方乱流
乱れの移流,生成,拡散がなく,ただ減衰していくだけの乱流を考えると,乱流エネルギー\(k\)および乱流散逸率\(\varepsilon\)の輸送方程式はそれぞれ次のようになる
\begin{equation}
\frac{\partial k}{\partial t}=-\varepsilon
\end{equation}
\begin{equation}
\frac{\partial \varepsilon}{\partial t}=-C_{\varepsilon_{2}}\varepsilon\frac{\varepsilon}{k}
\end{equation}
また,このような乱流の減衰初期には実験的に次の関係が確認されている
\begin{equation}
k \propto t^{-1}
\end{equation}
定数の決定
以上の仮定を用いて,標準k-εモデルの定数を決定していく
\(C_{\mu}\)
対数領域では \(\nu \ll \nu_{t}\)なので,せん断応力はレイノルズ応力に等しく,
\begin{equation}
\overline{uv}=-\nu_{t}\frac{\partial u}{\partial y}
\qquad\rightarrow\qquad
\nu_{t}=-\frac{\overline{uv}}{\frac{\partial u}{\partial y}}
\tag{i}
\end{equation}
対数領域では局所平衡 \(P_{k}=\varepsilon\) が成り立つので,
\begin{equation}
-\overline{uv}\frac{\partial u}{\partial y}=\varepsilon
\qquad\rightarrow\qquad
\frac{\partial u}{\partial y}=-\frac{\varepsilon}{\overline{uv}}
\tag{ii}
\end{equation}
(i)に(ii)を代入して,実験的に得られた式 \(|\overline{uv}|/k=0.3\)を代入すると
\begin{equation}
\nu_{t}=\frac{\left(\overline{uv}\right)^{2}}{\varepsilon}=0.09\frac{k^{2}}{\varepsilon}
\qquad\rightarrow\qquad
C_{\mu}=0.09 \qquad \left(\sqrt{C_{\mu}}=0.3\right)
\end{equation}
\(C_{\varepsilon_{2}}\)
一様等方乱流における乱流エネルギー\(k\)の輸送方程式および乱流散逸率\(\varepsilon\)の輸送方程式より,
\begin{equation}
\left\{\begin{array}{rl}
&\frac{\partial \varepsilon}{\partial t}=-C_{\varepsilon_{2}}\frac{1}{k}\varepsilon^{2} \\
&\varepsilon=-\frac{\partial k}{\partial t} \\
\end{array}\right.
\qquad\rightarrow\qquad
\frac{\partial^{2} k}{\partial t^{2}}=C_{\varepsilon_{2}}\frac{1}{k}\left(\frac{\partial k}{\partial t}\right)^{2}
\tag{iii}
\end{equation}
(iii)に,実験から得られた式 \(k=at^{-1}\)(\(a\)は任意定数)を代入すると
\begin{equation}
2at^{-3}=C_{\varepsilon_{2}}\frac{1}{at}\left(-at^{-1}\right)^{2}
\qquad\rightarrow\qquad
C_{\varepsilon_{2}}=2
\end{equation}
\(\sigma_{k}\),\(\sigma_{\varepsilon}\)
\(\sigma_{k}\)および\(\sigma_{\varepsilon}\)は,勾配拡散近似の係数であり,実験的に1.0に近い数値だと考えられる
\(C_{\varepsilon_{1}}\)
圧力勾配のない定常な2次元せん断乱流の対数領域では,\(\varepsilon\)の実質微分が0になり(\(\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}=0\)),分子粘性が無視でき(\(\nu \ll \nu_{t}\)),局所平衡 \(P_{k}=\varepsilon\)が成り立つので,\(\varepsilon\)の輸送方程式は次のようになる
\begin{equation}
0
=\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)\frac{\varepsilon^{2}}{k}+\frac{\partial}{\partial y}\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}\frac{\partial \varepsilon}{\partial y}\right)
\tag{iv}
\end{equation}
ここで,上記の式から\(\varepsilon\)と\(\nu_{t}\)を消去するために,対数速度分布を用いて\(\varepsilon\)を\(k\)で表すことを考える
対数速度分布の式 \(u^{+}=\frac{1}{\kappa}\ln{y^{+}}+B\)の両辺を\(y\)で微分して
\begin{equation}
\frac{\partial}{\partial y}\left(\frac{\overline{u}}{u_{\tau}}\right)
=\frac{\partial}{\partial y}\left(\frac{1}{\kappa}\ln{\frac{u_{\tau}y}{\nu}}+B\right)\qquad\rightarrow\qquad
\frac{\partial u}{\partial y}
=\frac{u_{\tau}}{\kappa y}
\end{equation}
局所平衡の式 \(\varepsilon=P_{k}\)に,対数速度分布における速度勾配を代入して,
\begin{equation}
\varepsilon=P_{k}=-\overline{uv}\frac{\partial u}{\partial y}
=-\overline{uv}\frac{u_{\tau}}{\kappa y}
\end{equation}
さらに,乱流境界層内でレイノルズ応力が一定(\(-\rho\overline{uv} \simeq \tau_{w} = \rho u_{\tau}^{2}\))という仮定を追加し,実験から得られた式 \(|\overline{uv}|=u_{\tau}^{2}=\sqrt{C_{\mu}}k\) を代入すると,次の式が得られる
\begin{equation}
\varepsilon=\frac{u_{\tau}^{3}}{\kappa y}
=\frac{C_{\mu}^{\frac{3}{4}}k^{\frac{3}{2}}}{\kappa y}
\tag{v}
\end{equation}
(v)より,\(\nu_{t}\)は次のようになる
\begin{equation}
\nu_{t}=C_{\mu}\frac{k^2}{\varepsilon}
=C_{\mu}\frac{k^{2}}{\frac{C_{\mu}^{3/4}k^{3/2}}{\kappa y}}
=C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}\kappa y
\tag{vi}
\end{equation}
(iv)に(v)と(vi)を代入し,\(k\)が\(y\)によらず一定だと仮定すると,
\begin{align}
&0=
\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)
\frac{\left(\frac{C_{\mu}^{3/4}k^{3/2}}{\kappa y}\right)^{2}}{k}
+\frac{\partial}{\partial y}\left(\frac{C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}\kappa y}{\sigma_{\varepsilon}}\frac{\partial}{\partial y}\left(\frac{C_{\mu}^{\frac{3}{4}}k^{\frac{3}{2}}}{\kappa y}\right)\right) \\
\rightarrow\qquad
&0=
\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)\frac{C_{\mu}^{3/2}k^{2}}{\kappa^{2} y^{2}}
+\frac{\partial}{\partial y}\left(-\frac{1}{\sigma_{\varepsilon}}\frac{C_{\mu}k^{2}}{y}\right) \\
\rightarrow\qquad
&0=\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)\frac{C_{\mu}^{3/2}k^{2}}{\kappa^{2} y^{2}}
+\frac{1}{\sigma_{\varepsilon}}\frac{C_{\mu}k^{2}}{y^{2}}
\end{align}
結局,以下の関係式が得られる
\begin{equation}
C_{\varepsilon_{2}}-C_{\varepsilon_{1}}
=\frac{\kappa^{2}}{\sigma_{\varepsilon}C_{\mu}^{1/2}}
\end{equation}
\(C_{\varepsilon_{1}}\),\(C_{\varepsilon_{2}}\),\(\sigma_{\varepsilon}\)は上記の関係式を満たすように決定する必要があり,すでにわかっている値として\(\kappa=0.4\),\(\sigma_{\varepsilon}=1.0\),\(C_{\varepsilon_{2}}=2.0\),\(C_{\mu}=0.09\)を代入すると,\(C_{\varepsilon_{1}}=1.5\)が得られる
標準k-εモデルの定数群はこれらの定数を各種計算によってさらに最適化したものである
壁面における取り扱い
標準k-εモデルはレイノルズ数が高く局所平衡が成り立つ対数領域をもとに定数を決定しているので,このままではより壁面に近い低レイノルズ数効果の大きい領域(粘性低層)を扱うことができない
CFDの計算を行うためには壁面の境界条件を必ず設定する必要があるので,次の2つの方法で壁面近傍の流れを取り扱っている
- 対数領域に第1格子点を設定し,壁面の境界条件として壁関数とよばれる関数を設定することで,粘性低層の計算を省略する
- 粘性低層に第1格子点を設定し,粘性低層の低レイノルズ数効果を取り扱えるように修正を加えた低レイノルズ数型モデルによって滑りなしの壁面境界条件を計算する
それぞれについて説明する
壁関数(Wall function)
壁面境界条件として壁関数を使う際は,第1格子点を対数領域(\(30 \leq y^{+} \leq 200\))に配置する
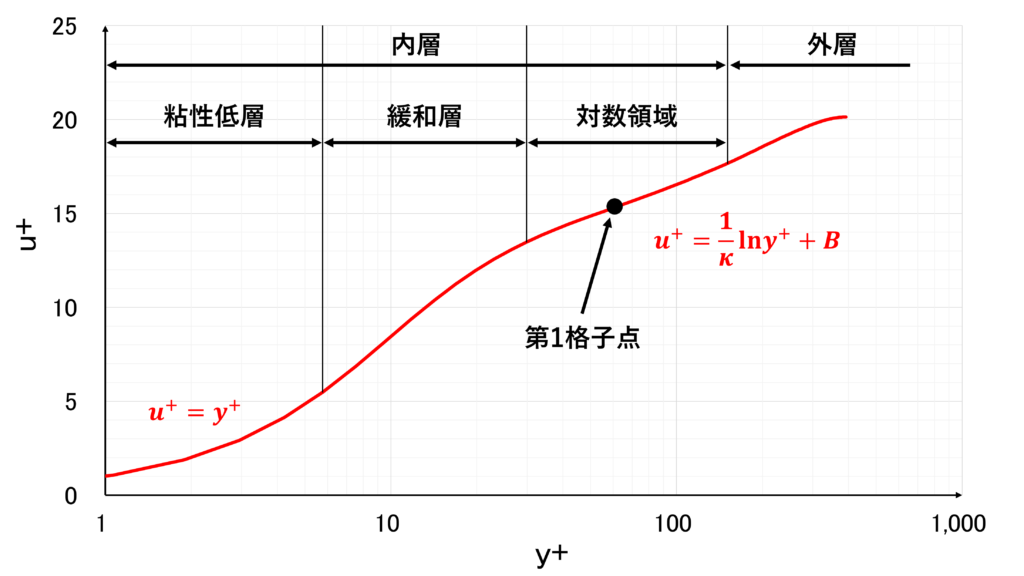
良かれと思って壁面近くの格子を細かくしすぎると,壁関数を使っているのに第1格子点が緩和層や粘性低層に入ってしまい逆に精度が悪くなるので注意が必要である
メリットとデメリットは以下の通り
- 壁面近傍の格子点数を減らすことで計算コストを抑えることができる
- 付着境界層については対数則を用いることで適切な境界条件を設定することができる
- 付着境界層以外の流れ場(境界層剥離・再付着,乱流遷移など)に対して高い精度を与える壁関数がない
- 1つの流れ場に存在しうる多様な壁面境界に対して1つの壁関数を与えるのは無理がある
- 熱伝達にかかわる温度境界層を取り扱えない
具体的な壁面境界条件としては,速度については \(u_{i}=0\),圧力については \(\frac{\partial p}{\partial n}=0\) を設定し,乱流エネルギー,乱流散逸率,渦粘性係数に関してはそれぞれに応じた壁関数を設定する
対数速度分布から\(u\)を計算することもできるが,CFDでは \(u_{i}=0\) と与えても問題ない
壁面上の\(\nu_{t}\)の値は\(k\)と\(\varepsilon\)の壁関数を与えた時点で計算できるが,CFDでは数値計算の都合上\(\nu_{t}\)にも壁関数を適用する
代表的な壁関数について説明する(第1格子点を表す添え字を\(_{P}\)とする)
摩擦速度\(u_{\tau}\)
対数速度分布の式 \(u^{+}=\frac{1}{\kappa}\mathrm{ln}y^{+}+B\)より,関数\(F(u_{\tau})\)を定義すれば,ニュートン法などの反復計算によって\(u_{\tau}\)が計算できる
\begin{equation}
F(u_{\tau})=\frac{u_{P}}{u_{\tau}}-\frac{1}{\kappa}\mathrm{ln}\frac{u_{\tau}y_{P}}{\nu}-B=0, \quad\rightarrow\quad
u_{\tau}^{n+1}=u_{\tau}^{n}-\frac{F(u_{\tau}^{n})}{F'(u_{\tau}^{n})}
\end{equation}
もしくは,対数領域において実験的に \(|uv|=\sqrt{C_{\mu}}k\) が成立し,粘性低層と対数領域でせん断応力が一定 \(|uv|=\tau_{w}/\rho=u_{\tau}^{2}\) であると仮定すれば次のようにも計算できる
\begin{equation}
u_{\tau}=\sqrt{|uv|}=C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}
\end{equation}
乱流エネルギー\(k\)
同様の仮定において\(k_{P}\)は次のように計算できる
\begin{equation}
k_{P}=\frac{u_{\tau}^{2}}{\sqrt{C_{\mu}}}=const.
\quad\rightarrow\quad
\frac{\partial k_{P}}{\partial y_{P}}=0
\end{equation}
乱流散逸率\(\varepsilon\)
上記の仮定にさらに局所平衡 \(\varepsilon=P_{k}\)を加えると,\(\varepsilon_{P}\)は次のように計算できる( 標準k-εモデルの定数群の決定方法 を参照)
\begin{equation}
\varepsilon_{P}=\frac{u_{\tau}^{3}}{\kappa y_{P}}
=\frac{C_{\mu}^{\frac{3}{4}}k_{P}^{\frac{3}{2}}}{\kappa y_{P}}
\end{equation}
渦粘性係数\(\nu_{t}\)
対数速度分布は次のように書き換えることができる
\begin{equation}
u^{+}=\frac{1}{\kappa}\mathrm{ln}\left(Ey^{+}\right) \qquad \left(E=9.8\right)
\end{equation}
上記の対数速度分布から\(u_{\tau}\)を計算する
\begin{equation}
\frac{u}{u_{\tau}}=\frac{1}{\kappa}\mathrm{ln}\left(Ey^{+}\right)
\quad\rightarrow\quad
u_{\tau}=\frac{\kappa u}{\mathrm{ln}\left(Ey^{+}\right)}
\tag{i}
\end{equation}
壁面せん断応力 \(\tau_{w}=\rho u_{\tau}^{2}\)の式に(i)を代入し,第1格子点における速度勾配 \(\left(\frac{\partial u}{\partial y}\right)_{P}=\frac{u_{P}-0}{y_{P}-0}=\frac{u_{P}}{y_{P}}\) をくくりだす
\begin{equation}
\tau_{w}=\rho u_{\tau}^{2}
=\rho u_{\tau}\frac{\kappa u_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}
=\frac{\rho\kappa u_{\tau} y_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}\frac{u_{P}}{y_{P}}
=\frac{\mu \kappa y^{+}_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}\frac{u_{P}}{y_{P}}
\end{equation}
上記の式と壁面せん断応力の別表式 \(\tau_{w}=\left(\mu+\mu_{t_{P}}\right)\frac{u_{P}}{y_{P}}\) を比較して両辺を\(\rho\)で割ることで,渦粘性係数の壁関数を求めることができる
\begin{equation}
\mu+\mu_{t_{P}}=\frac{\mu \kappa y^{+}_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}
\quad\rightarrow\quad
\nu_{t_{P}}=\nu\left(\frac{\kappa y^{+}_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}-1\right)
\end{equation}
参考
低Re数型モデル
低Re数型モデルを使うときは,第1格子点を粘性低層(\(y^{+} \leq 2 \sim 4\))に配置して,滑りなし境界条件を設定する
メリットとデメリットは以下の通り
- 熱伝達にかかわる温度境界層を取り扱うことができる
- 壁面近傍の格子点数が増えることで計算コストが増加する
具体的な壁面境界条件としては,速度については \(u_{i}=0\),圧力については \(\frac{\partial p}{\partial n}=0\) ,渦粘性係数については\(\nu_{t}=0\),乱流エネルギーについては \(k=0\) ,乱流散逸率については\(\varepsilon=\tilde{\varepsilon}+D=\frac{2\nu k}{y^{2}}\)を設定する
RANSのメリットは計算コストが低いことなので,計算コストの高い低Re数型モデルは壁面近傍の乱れの挙動が特に重要となる流れ場(伝熱を伴う温度境界層など)以外ではあまり使われることはない
基本形
一般的な低レイノルズ数型モデルは次のように表される
\begin{equation}
\nu_{t}=C_{\mu}f_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\left(\tilde{\varepsilon}+D\right)
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
\begin{equation}
\frac{\partial \tilde{\varepsilon}}{\partial t}+\overline{u}_{j}\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}f_{1}P_{k}-C_{\varepsilon_{2}}f_{2}\tilde{\varepsilon}\right)\frac{\tilde{\varepsilon}}{k}+E+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}\right\}
\end{equation}
ここで,\(f_{\mu}\)は\(\nu_{t}\)に対する減衰関数,\(f_{1}\)および\(f_{2}\)は\(\varepsilon\)の生産項および消滅項における補正関数,\(D\)および\(E\)は壁面補正項である
ここで,粘性散逸率の真の値は壁面補正項\(D\)を用いて \(\varepsilon=\tilde{\varepsilon}+D\) として計算される
参考までに,代表的な低レイノルズ数型モデルを以下に示す
| モデル | \(f_{\mu}\) | \(f_{1}\) | \(f_{2}\) | \(D\) | \(E\) | \(C_{\mu}\) | \(C_{\varepsilon_{1}}\) | \(C_{\varepsilon_{2}}\) | \(\sigma_{k}\) | \(\sigma_{\varepsilon}\) |
| 標準k-ε | \(1.0\) | \(1\) | \(1\) | \(0\) | \(0\) | \(0.09\) | \(1.44\) | \(1.92\) | \(1.0\) | \(1.3\) |
| Launder-Sharma | \(\exp{\left[\frac{-3.4}{\left\{1+\left(R_{t}/50\right)\right\}^{2}}\right]}\) | \(1\) | \(1-0.3\exp\left(-R_{t}^{2}\right)\) | \(2\nu\left(\frac{\partial \sqrt{k}}{\partial t}\right)^{2}\) | \(2\nu\nu_{t}\left(\frac{\partial^{2} \overline{u}}{\partial y^{2}}\right)^{2}\) | \(0.09\) | \(1.44\) | \(1.92\) | \(1.0\) | \(1.3\) |
| Lam-Bremhorst | \(\left\{1-\exp{\left(-0.0165R_{y}\right)}\right\}^{2}\left(1+\frac{20.5}{R_{t}}\right)\) | \(1+\left(\frac{0.05}{f_{\mu}}\right)^{3}\) | \(1-\exp{\left(-R_{t}^{2}\right)}\) | \(0\) | \(0\) | \(0.09\) | \(1.44\) | \(1.92\) | \(1.0\) | \(1.3\) |
| Lien-Leschziner | \(\left\{1-\exp{\left(-0.016R_{y}\right)}\right\}/\left\{1-\exp{\left(-0.263R_{y}\right)}\right\}\) | \(1\) | \(1-0.3\exp{\left(-R_{t}^{2}\right)}\) | \(0\) | \(\frac{C_{\varepsilon_{2}}C_{\mu}^{\frac{3}{4}}f_{2}\sqrt{k}\varepsilon\exp{\left(-0.00222R_{y}^{2}\right)}}{0.41y\left\{1-\exp{\left(-0.263R_{y}\right)}\right\}}\) | \(0.09\) | \(1.44\) | \(1.92\) | \(1.0\) | \(1.3\) |
| Abe-Kondoh-Nagano | \(\left\{1-\exp{\left(\frac{-y^{*}}{14}\right)}\right\}^{2}\left[1+\frac{5}{R_{t}^{3/4}}\exp{\left\{-\left(\frac{R_{t}}{200}\right)^{2}\right\}}\right]\) | \(1\) | \(\left\{1-\exp{\left(\frac{-y^{*}}{3.1}\right)}\right\}^{2}\left[1-0.3\exp{\left\{-\left(\frac{R_{t}}{6.5}\right)^{2}\right\}}\right]\) | \(0\) | \(0\) | \(0.09\) | \(1.5\) | \(1.9\) | \(1.4\) | \(1.4\) |
R_{t}=\frac{k^2}{\nu\varepsilon}, \qquad
R_{y}=\frac{\sqrt{k}y}{\nu}, \qquad
y^{*}=\frac{y}{\left(\nu^{3}/\varepsilon\right)^{1/4}}
\end{equation}
壁面漸近挙動
壁面の極近傍に乱れの挙動を壁面漸近挙動といい,低レイノルズ数型モデルの補正項はこの壁面漸近挙動を満たすように決める必要がある
変動速度の各方向成分\([u', v', w']\)を壁面からの垂直距離\(y\)についてテイラー展開すると次のようになる
\begin{equation}
\left\{\begin{array}{rcl}
u'(y)&=&a_{0}+a_{1}y+a_{2}y^{2}+a_{3}y^{3}+\cdots \\
v'(y)&=&b_{0}+b_{1}y+b_{2}y^{2}+b_{3}y^{3}+\cdots \\
w'(y)&=&c_{0}+c_{1}y+c_{2}y^{2}+c_{3}y^{3}+\cdots \\
\end{array}\right.
\end{equation}
壁面上での滑りなし条件 \(u'(0)=v'(0)=w'(0)=0\)および壁面上での連続の式\(\frac{\partial u'}{\partial x}(0)=\frac{\partial v'}{\partial y}(0)=\frac{\partial w'}{\partial z}(0)=0\)より,変動速度の各方向成分の壁面漸近挙動が得られる
\begin{equation}
\left\{\begin{array}{rcll}
u'(y)&=&a_{1}y&+a_{2}y^{2}+a_{3}y^{3}+\cdots \\
v'(y)&=& &\quad b_{2}y^{2}+b_{3}y^{3}+\cdots \\
w'(y)&=&c_{1}y&+c_{2}y^{2}+c_{3}y^{3}+\cdots \\
\end{array}\right.
\tag{i}
\end{equation}
(i)を用いると,壁面における各乱流諸量の\(y\)についてのテイラー展開は次のようになる
(乱流エネルギー)
\begin{align}
k=\frac{1}{2}\left(\overline{u'u'}+\overline{v'v'}+\overline{w'w'}\right)
\quad\rightarrow\quad k(y)=\frac{1}{2}\left(a_{1}^{2}+c_{1}^{2}\right)y^{2}+\cdots
\end{align}
(乱流散逸率)
\begin{align}
&\varepsilon=\nu\left(\overline{\frac{\partial u'}{\partial y}\frac{\partial u'}{\partial y}}+\overline{\frac{\partial v'}{\partial y}\frac{\partial v'}{\partial y}}+\overline{\frac{\partial w'}{\partial y}\frac{\partial w'}{\partial y}}\right)
\quad\rightarrow\quad \varepsilon(y)=\nu\left(a_{1}^{2}+c_{1}^{2}\right)+\cdots
\end{align}
(レイノルズ応力のuv成分)
\begin{align}
-\overline{u'v'}(y)=a_{1}b_{2}y^{3}+\cdots
\end{align}
(渦粘性係数)
\begin{align}
&\nu_{t}=\frac{-\overline{uv}}{\partial u/\partial y}
\quad\rightarrow\quad \nu_{t}(y)=\frac{a_{1}b_{2}y^{3}+\cdots}{a_{1}+\cdots}
\end{align}
よって,それぞれの壁面漸近挙動は,\(k \propto y^{2}\),\(\varepsilon \propto y^{0}\),\(\overline{u'v'} \propto y^{3}\),\(\nu_{t} \propto y^{3}\)である
壁面境界条件
前節で求めた壁面上での乱流諸量のテイラー展開に \(y=0\) 代入することで,低レイノルズ数型モデルにおける壁面境界条件(添え字\(_{w}\))を求めることができる
(乱流エネルギー)
\begin{equation}
k_{w}=0
\end{equation}
(乱流散逸率)
\begin{equation}
\varepsilon_{w}=\nu\left(a_{1}^{2}+c_{1}^{2}\right)
=\left\{\begin{array}{l}
\nu\frac{\partial^{2} k(y)}{\partial y^{2}} \\
\nu\left(\frac{\partial \sqrt{k(y)}}{\partial y}\right)^{2} \\
2\nu\frac{k(y)}{y^{2}} \\
\end{array}\right.
\end{equation}
(渦粘性係数)
\begin{equation}
\nu_{t_{w}}=0
\end{equation}
\(\varepsilon\)の壁面境界条件の与え方は3通りあるが,CFDでは境界端での微分の精度が確保できないことから,微分の必要がない \(\varepsilon_{P}=\frac{2\nu k_{P}}{y_{P}^{2}}\) の境界条件が使われる
ただし,Launder-Sharmaモデルのように低レイノルズ数型モデルの補正項として\(D\)項を用いている場合は \(\varepsilon_{w}=\tilde{\varepsilon}_{w}+D=\frac{2\nu k}{y^{2}}\)なので,\(\tilde{\varepsilon}\)の壁面境界条件として \(\tilde{\varepsilon}_{w}=0\) を設定する必要がある
非線形渦粘性モデル(Non-Linear Eddy Viscosity Model)
渦粘性モデルの欠点は,レイノルズ応力の顕著な異方性,回転,曲率,衝突,剥離がある流れや変動速度の各成分間の配分が特徴づける流れ(ex.矩形ダクト内の第二次第二種流れ)を精度良く扱うことができないことである
この問題を解決するために開発されたのが非線形渦粘性モデルである
基本形
非線形渦粘性モデルでは,レイノルズ応力\(\tau_{ij}\)を次のように計算する
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\tag{1}
\end{equation}
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}+2k b_{ij}
\end{equation}
ここで,\(b_{ij}\)は非等方テンソルと呼ばれ,線形渦粘性モデルにおける \(-\nu_{t}S_{ij}\) を非線形に拡張した項である
\(b_{ij}\)は\(S_{ij}\)や\(\Omega_{ij}\)などの非線形項で構成され,高次のRANSモデルである応力方程式モデルなどを参考にして決定される
非線形モデルの例として,以下の記事で実装したAJLモデルを紹介する
非線形項の実装
非線形渦粘性モデルをCFDで実装する際は,非等方テンソル\(b_{ij}\)を線形モデルとそれに付加する非線形項\(N_{ij}\)に分解し,追加の非線形項\(N_{ij}\)は外力項としてNavier-Stokes方程式に組み込まれる
\begin{equation}
b_{ij}=-\nu_{t}S_{ij}+N_{ij}
\end{equation}
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
+\frac{\partial}{\partial x_{j}}N_{ij}
\end{equation}
追加の非線形項を外力項として組み込むことで,プログラムをいじることなく線形渦粘性モデルを非線形モデルに拡張することができる
k-εモデルは,渦粘性係数を乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)から計算するモデルである
\(k\)と\(\varepsilon\)はそれぞれ輸送方程式を解くことによって計算する
計算コスト,精度,扱いやすさの面からもっとも広く普及しているモデルである
標準k-εモデルでは壁関数という関数を壁面境界条件に設定するが,低レイノルズ数型モデルを使えば壁面近傍に滑りなし条件を設定して計算できる
より複雑な流れ場を扱うために非線形渦粘性モデルも開発されており,非線形項は外力項として実装される
まとめ
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(1)に関連して,モデル化の手法の1つであるRANSについて説明した
RANSは渦粘性モデルと応力方程式モデルに分けられる
渦粘性モデルの中でも,標準k-εモデルが広く普及しており,簡単な流れ場に対しては高い精度と計算コストの低さを実現できる
その他にも様々な派生形があり,計算する流れ場に応じて適したモデルを選択する必要がある
使用するモデルについては非常に迷うところだが,参考文献の1つである「乱流の数値シミュレーション 改訂版」では次のように述べられている
既に膨大な研究があるが,あらゆる乱流場に適用できるような普遍的なモデルは得られていない.この本で推奨する選択としては,「簡単な流れ」にはk-εモデル,それ以外には7章で述べるラージエディシミュレーションを使うということである.
乱流の数値シミュレーション 改訂版 p.177
次回はもう1つの乱流モデル手法であるLES(Large Eddy Simulation)について説明する
↓まとめ記事
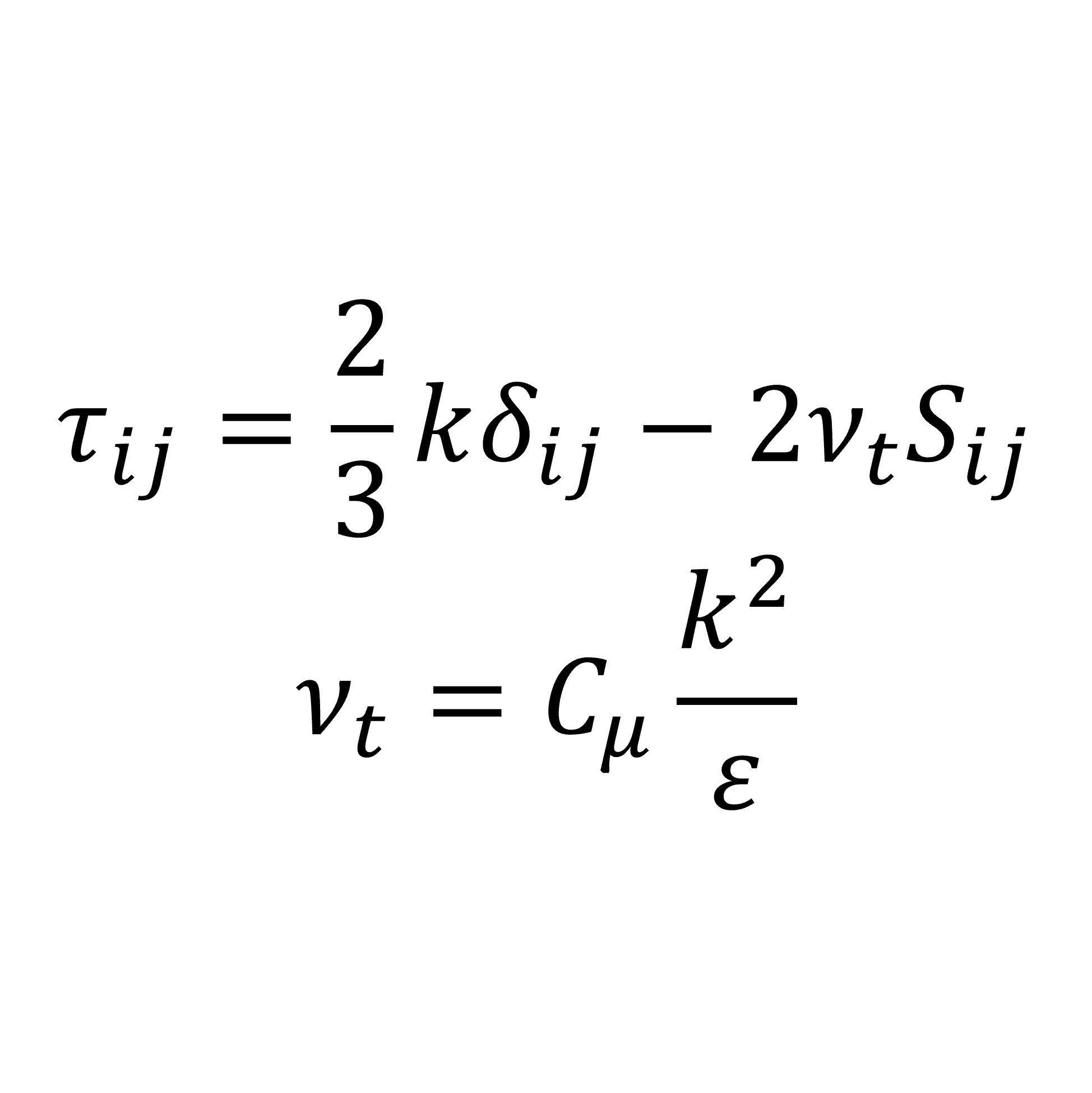

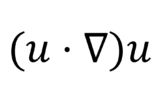
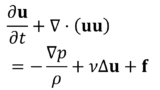


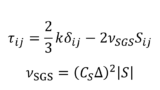

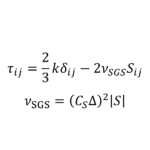
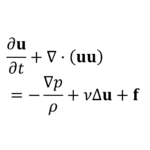
コメント
すばらしいブログありがとうございます。
院生で熱流体解析を触る必要が出てきて、勉強に利用させていただいています。
一つ質問があります。k-εモデルにおける各項のモデル化の部分で生成項P_kのモデル化に関する記述がありませんが、
モデル化が必要ないのでしょうか。
お手数おかけしますが、ご教授いただければ幸いです。
コメントいただきありがとうございます。
生成項P_kのモデル化についての記述を追加しました。