CFDにおける境界条件(流入条件/流出条件/滑りなし条件/周期境界条件)について説明を行う
keyword: 格子生成,流入条件,流出条件,滑りなし条件,初期条件
境界条件
境界条件には大きく分けて値指定境界条件(ディリクレ境界条件)と勾配指定境界条件(ノイマン境界条件)がある
主な境界面には流入面,流出面,壁面の3つの種類があり,それぞれの面における速度,圧力,スカラー量(\(k\)や\(\varepsilon\))に対して,値指定境界条件か勾配指定境界条件のどちらかが設定される
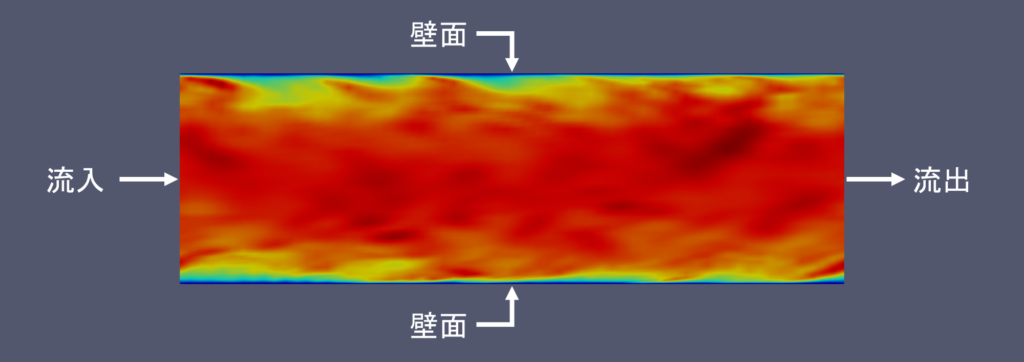
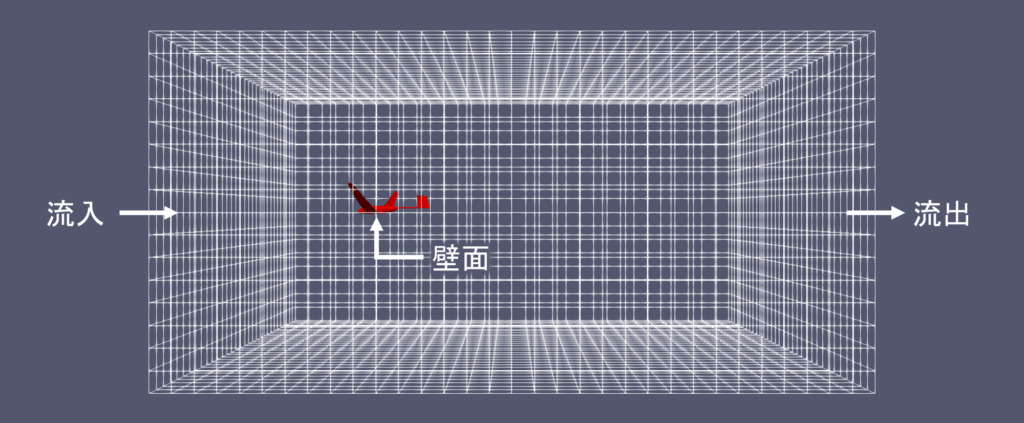
流入条件
流入条件は,流入面に適用する境界条件である
それぞれの物理量に適用する条件は次の通り
| 速度 \(U_{i}\) | 圧力 \(p\) | 渦粘性係数 \(\nu_{t}\) | 乱流エネルギー \(k\) | 乱流散逸率 \(\varepsilon\) |
| 値指定 | ゼロ勾配指定 | 値指定 | 値指定 | 値指定 |
値指定でどのような値を指定するかは乱流モデルによって異なる
RANS
RANSの場合はほとんどが定常流なので,内部流れなら何かしらの解析結果や実験結果から得られた\(U_{i}\),\(\nu_{t}\),\(k\),\(\varepsilon\)の値の分布を直接与え,外部流れなら一様流の値を指定すればいい
流入面の直後では多少不自然なふるまいをすることがあるので,解析対象に影響を与える前に十分な助走区間を設ける必要がある
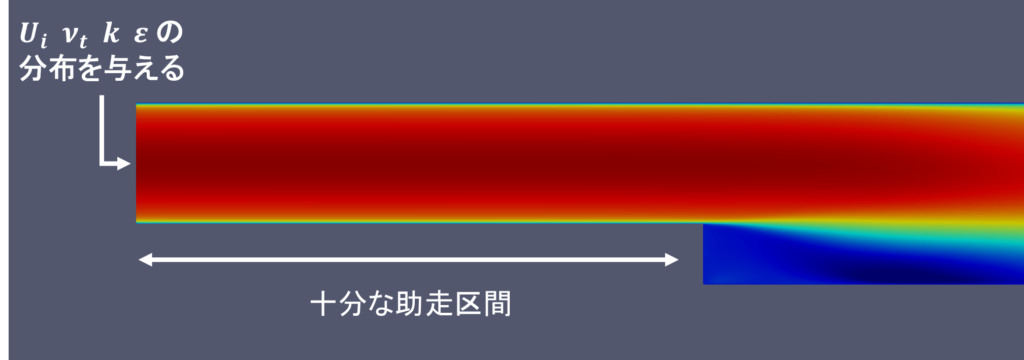
LES
LESの場合は非定常流れなので,流入面でも非定常に変化する値を与える必要がある
だが,そもそも非定常に乱れる流れの値がわからないからCFDで計算しているのであって,流入面で非定常な流れの値を指定できるようならCFDの計算を行う必要はない
よって,LESでは次のように流入面における値を設定する
- RANSなどで計算した平均分布に乱数を加えて疑似的な乱れを与える
- さらに上流に流れを乱すような障害物を置いて,流入面の位置で発達した乱流になるようにする
- 上流にドライバ部として周期境界条件を用いた乱流流れを計算し,ドライバ部のある断面における値を流入面の値をして使用する
(1)や(2)の方法は乱れが発達するまでに長い助走区間が必要であり,数値計算が不安定になりやすい
(3)の方法はドライバ部の分だけ計算の負荷が増加してしまう
↓ドライバ部を用いた計算についての詳細はこちら
- 流入条件の設定は使用する乱流モデルによって異なる
- RANSでは,\(U_{i}\),\(\nu_{t}\),\(k\),\(\varepsilon\)の値の分布を直接与え,解析対象の前に助走区間を設ける
- LESでは,疑似乱数で乱れを生成する,風上に置いた障害物で乱れを生成する,流入面で乱流流れを計算する,のいずれかの方法をとる
↓乱流モデルについて
流出条件
流出条件は,流出面に適用する境界条件である
それぞれの物理量に適用する条件は次の通り
| 速度 \(U_{i}\) | 圧力 \(p\) | 渦粘性係数 \(\nu_{t}\) | 乱流エネルギー \(k\) | 乱流散逸率 \(\varepsilon\) |
| ゼロ勾配指定 | 値指定 | ゼロ勾配指定 | ゼロ勾配指定 | ゼロ勾配指定 |
ゼロ勾配指定は十分に発達した流れを想定しているため,流出面は解析対象から十分に離した位置に設定する必要がある
圧力については数値流体力学の支配方程式で勾配\(\nabla p\)しか関与していないため,相対的な値しか計算には必要ない
圧力の具体的な値の計算を行うにはどこかに圧力の基準値を設定する必要があり,流出面がある場合は流出面で基準値 \(p=0\) が指定される
- 流出条件では,解析対象から十分離れた風下でゼロ勾配条件を指定する
- 圧力のみ値指定をして圧力の基準値を設定する
周期境界条件
周期境界条件は,周期的に繰り返すような形状に対する解析に用いる境界条件で,流入面と流出面に適用する境界条件である
例えば,次に示すような周期的に繰り返される形状に対して流入面と流出面に周期境界条件を設定すれば,流出面から出て言った流れ場が流入面から入ってくるような計算を行うことができる

参考
≫User Guide: Periodic hill - OpenFOAM
それぞれの物理量に適用する条件は次の通り
| 速度 \(U_{i}\) | 圧力 \(p\) | 渦粘性係数 \(\nu_{t}\) | 乱流エネルギー \(k\) | 乱流散逸率 \(\varepsilon\) |
| 周期境界 | 周期境界 | 周期境界 | 周期境界 | 周期境界 |
流入面から入ってきた流れは流出面に至るまでに減速され,減速した流れが再び流入面から入ってきてしまうと流れはさらに減速されてしまう
周期境界条件において流れが減速され続けてしまうことを防ぐために,周期境界条件を適用する際は次の手法をとることで断面平均流速を維持する必要がある
- 圧力勾配を加える
- 運動量をソース項として加える
- 周期境界条件とは,繰り返しを含む流れ場を計算するための条件である
- 流出面から出て行った流れがそのまま流入面から入ってくるので,流れが減衰しないように圧力勾配か運動量のソース項を追加する必要がある
滑りなし条件
滑りなし条件は,壁面に適用する境界条件である
それぞれの物理量に適用する条件は次の通り
| 速度 \(U_{i}\) | 圧力 \(p\) | 渦粘性係数 \(\nu_{t}\) | 乱流エネルギー \(k\) | 乱流散逸率 \(\varepsilon\) |
| 値指定 | ゼロ勾配指定 | 値指定 | 値指定 | 値指定 |
速度の値指定は \(u_{i}=0\)とし,\(\nu_{t}\),\(k\),\(\varepsilon\)の値指定でどのような値を指定するかは乱流モデルによって異なる
RANS
一般的なRANSモデルでは,壁面近傍の第1格子点を対数流域に設定し,\(\nu_{t}\),\(k\),\(\varepsilon\)の壁面の境界条件として壁関数を用いる
↓壁関数についてはこちら
低レイノルズ数型RANS
低レイノルズ数型RANSモデルでは,壁面近傍の第1格子点を粘性低層に設定し,壁面の境界条件として \(\nu_{t}=0\),\(k=0\),\(\varepsilon=\frac{2\nu k}{y^2}\) を用いる
↓導出についてはこちら
LES
LESでは,壁面近傍の第1格子点を粘性低層に設定し,壁面の境界条件として \(\nu_{t}=0\),\(k=0\) を用いる(LESでは\(\varepsilon\)の輸送方程式を解かないので境界条件は必要ない)
- 壁面では滑りなし境界条件を使う
- 境界条件の細かい設定は使用する乱流モデルによって異なる
まとめ
CFDにおける境界条件(流入条件/流出条件/滑りなし条件/周期境界条件)について説明を行った
↓関連記事






コメント