主翼の空力構造計算を線形解析で行う
渦格子法を拡張したようなプログラムになる
目的
今回の目的は,主翼の空力構造計算を線形解析で行うことである.
計算手法については次の論文を参考にした
≫揚力線理論を拡張した地面効果域における翼の空力計算手法,西出憲司,第12回スカイスポーツシンポジウム
プログラムの大部分は非線形解析の使いまわしなので,次の記事を参考にしてほしい.
計算手法
計算手法について説明する.
式番号については参考文献と同じものを用いる.
まず,i番目のパネルにおける局所揚力係数\(C_{l}(i)\)は,揚力傾斜\(a_{0}(i)\)と誘導迎角\(\alpha_{ind}(i)\)を用いて次のように表せる.
\begin{eqnarray}
C_{l}(i)=C_{l_{0}}(i)+a_{0}(i)\alpha_{ind}(i)
\tag{2}
\end{eqnarray}
ここで,\(C_{l_{0}}(i)\)は,誘導速度がない場合の局所揚力係数である.
誘導迎角\(\alpha_{ind}(i)\)は,速度\(U_{0}\)と誘導速度\(w_{ind}(i)\)を用いると次のように表せる.
\begin{eqnarray}
\alpha_{ind}(i)=-arctan(\frac{w_{ind}(i)}{U_{0}}) \simeq -\frac{w_{ind}(i)}{U_{0}}
\tag{4}
\end{eqnarray}
式(4)を式(2)に代入すると,次のようになる.
\begin{eqnarray}
C_{l}(i)=C_{l_{0}}(i)-a_{0}(i)\frac{w_{ind}(i)}{U_{0}}
\tag{5}
\end{eqnarray}
誘導速度\(w_{ind}(i)\)は,TR-797の解説より,次のように表せる.
\begin{eqnarray}
w_{ind}(i)=\frac{1}{4\pi}\sum Q(i,j) \Gamma (j)
\tag{11'}
\end{eqnarray}
また,局所揚力係数\(C_{l}(i)\)と循環\(\Gamma (i)\)の関係は次のように表せる.
\begin{eqnarray}
\frac{1}{2}\rho U_{0}^{2} c(i)\Delta y C_{l}(i) &=& \frac{1}{2}\rho U_{0}^{2} \Delta y \Gamma (i) \\
C_{l}(i) &=& \frac{2}{c(i)U_{0}}\Gamma (i)
\tag{8'}
\end{eqnarray}
式(8’)と式(11’)を式(5)に代入すると次のようになる
\begin{eqnarray}
\frac{2}{c(i)U_{0}}\Gamma (i)=C_{l_{0}}(i)-\frac{a_{0}}{4\pi U_{0}}\sum Q(i,j)\Gamma (j)
\tag{12'}
\end{eqnarray}
式(12’)を次のように変形する
\begin{eqnarray}
4\pi U_{0}\frac{C_{l_{0}}(i)}{a_{0}(i)}=\frac{8\pi}{c(i) a_{0}(i)}\Gamma (i)+\sum Q(i,j)\Gamma(j)
\tag{13'}
\end{eqnarray}
ここで,行列\({\bf A}\),\({\bf B}\)を次のように定義する
\begin{eqnarray}
A(i,j) &=&
\begin{cases}
Q(i,j) \ \ (i \neq j) \\
\frac{8\pi}{c(i)a_{0}(i)}+Q(i,j) \ \ (i=j)
\end{cases}
\tag{14'} \\
B(i) &=& 4\pi U_{0}\frac{C_{l_{0}}(i)}{a_{0}(i)}
\tag{15}
\end{eqnarray}
よって,式(13’)は,循環\({\bf \Gamma}\)を未知数とした次の行列式になる
\begin{eqnarray}
B(i) &=& \sum A(i,j)\Gamma{j}
\tag{16} \\
{\bf B} &=& {\bf A}{\bf \Gamma}
\tag{17}
\end{eqnarray}
式(14’)と(15’)の係数行列\({\bf A}\),\({\bf B}\)を計算して式(17)の行列式を解くことで,スパン方向の循環分布を求めることができる.
フローチャート
今回のプログラムのフローチャートを以下に示す
空力構造計算の反復回数は2回で,1回目に変形してない状態の翼の計算を行い,そこで得られてたわみとねじれを考慮して2回目の翼の計算を行う
※反復回数は3回以上のほうが良いが,とりあえず最低限の2回で行う(理由は後述)
非線形解析のプログラムから取り除かれた処理を水色,追加された処理をオレンジで示してある
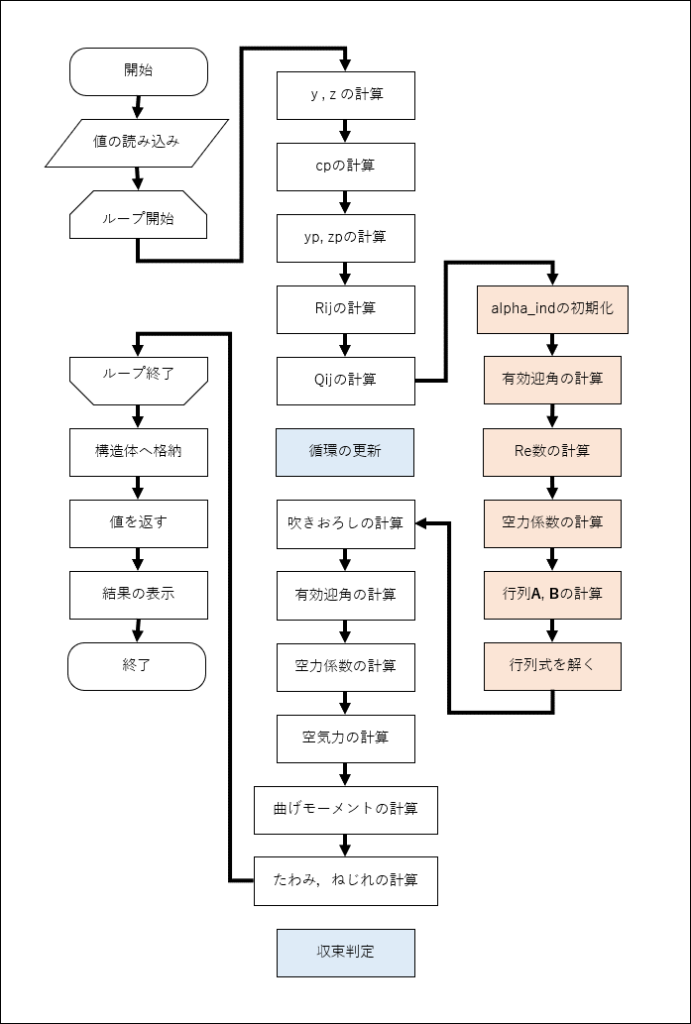
alpha_indを初期化したあとに有効迎角を計算して空力係数を計算することで,誘導迎角がないときの局所揚力係数\(C_{l_{0}}(i)\)を計算している
プログラムの解説
詳しい解説は主翼の空力および構造計算で行っているので,ここではコードを張り付けるのみにとどめる
Public Function 線形VLM_wing(p As Integer, ByRef Wing As Specifications, ByRef state As variables) As Specifications
'LLT
Call read_value_from_sheet(Wing, state, chord, chord_cp, dW(), setting_angle0(), foil_mixture, dihedral_angle0, Eix, GJ(), Cl_coef, Cdp_coef, Cm_coef)
'LLTの反復計算
For iteration = 0 To iteration_max
Call calculation_yz(Wing, state, y, z, setting_angle0, setting_angle, phi, dihedral_angle0, dihedral_angle, theta)
Call calculation_cp(Wing, state, cp, y, z)
Call calculation_ypzp(Wing, state, yp, zp, ymp, zmp, cp, dihedral_angle)
Call calculation_Rij(Wing, state, ds, yp, zp, ymp, zmp, Rpij, Rmij, Rpijm, Rmijm)
Call calculation_Qij(Wing, state, ds, yp, zp, ymp, zmp, Rpij, Rmij, Rpijm, Rmijm, dihedral_angle, Qij)
ReDim alpha_induced(2 * Wing.span_div - 1)
Call calculation_alpha_effective(Wing, state, alpha_effective, alpha_induced, cp, dihedral_angle, setting_angle, alpha_max, alpha_min)
Call calculation_Re(Wing, state, Re, cp, chord_cp, Re_max, Re_min)
Call calculation_aerodynamic_coefficient(Wing, state, CL, Cdp, Cm_ac, a0, a1, Cda, Cm_cg, dN, dT, dL, dDp, dM_cg, dM_ac, cp, chord_cp, setting_angle, alpha_effective, Re, dihedral_angle, foil_mixture, Cl_coef, Cdp_coef, Cm_coef)
'行列A,Bを計算
ReDim matrix1(2 * Wing.span_div - 1, 2 * Wing.span_div - 1)
ReDim matrix2(2 * Wing.span_div - 1)
For i = 0 To 2 * Wing.span_div - 1
For j = 0 To 2 * Wing.span_div - 1
'行列Aの計算
If i = j Then
matrix1(i, j) = (8 * pi) / (chord_cp(i) * a1(i)) + Qij(i, j)
Else
matrix1(i, j) = 0 + Qij(i, j)
End If
Next j
'行列Bの計算
matrix2(i) = 4 * pi * (state.Vair - rad * state.r * cp(1, i)) * CL(i) / a1(i)
Next i
'境界条件の方程式を解いて循環を求める
answer = ans(2 * Wing.span_div, matrix1, matrix2)
For i = 0 To 2 * Wing.span_div - 1
circulation(i) = answer(i)
Next i
Call calculation_downwash(Wing, state, circulation, Qij, alpha_induced, cp, wi)
Call calculation_alpha_effective(Wing, state, alpha_effective, alpha_induced, cp, dihedral_angle, setting_angle, alpha_max, alpha_min)
Call calculation_aerodynamic_coefficient(Wing, state, CL, Cdp, Cm_ac, a0, a1, Cda, Cm_cg, dN, dT, dL, dDp, dM_cg, dM_ac, cp, chord_cp, setting_angle, alpha_effective, Re, dihedral_angle, foil_mixture, Cl_coef, Cdp_coef, Cm_coef)
Call calculation_Force(Wing, state, iteration, Lift, Induced_Drag, cp, circulation, dihedral_angle, wi, CL, chord_cp)
Call calculation_Moment(Wing, state, Bending_Moment, Bending_Moment_T, Shear_Force, Torque, dN, dT, dM_cg, dW, dihedral_angle, cp, y, z)
Call calculation_deflection(Wing, state, deflection, theta, phi, Bending_Moment, Torque, Eix, GJ)
Call change_mode(Wing, state, dihedral_angle, dihedral_angle0, deflection, theta, phi, dM_ac, dM_cg, Shear_Force, Bending_Moment, Bending_Moment_T, Torque)
Next iteration
If iteration > iteration_max Then
iteration = iteration_max
End If
Call input_data_to_type(Wing, state, iteration, dihedral_angle, chord_cp, y, cp, a0, a1, Cda, dDp, dN, dT, dM_ac, CL, Cdp, Lift, Induced_Drag)
線形VLM_wing = Wing
If p = 1 Then
sht1.Range("AS2") = iteration
Call output_data_to_sheet(Wing, alpha_effective, Re, CL, Cdp, Cm_ac, a0, Cda, Cm_cg, setting_angle, dihedral_angle, circulation, wi, alpha_induced, y, z, deflection, theta, phi, Shear_Force, Bending_Moment, Torque, Bending_Moment_T)
End If
End Functionなお,変数の宣言の部分は省略してある
プログラムの実行
それでは実際に実行してみる
迎角-8度から14.5度まで0.5度刻みで計算したところ,実行時間は非線形解析では,線形解析では23.63秒となった167.30秒となった
結果を以下に示す
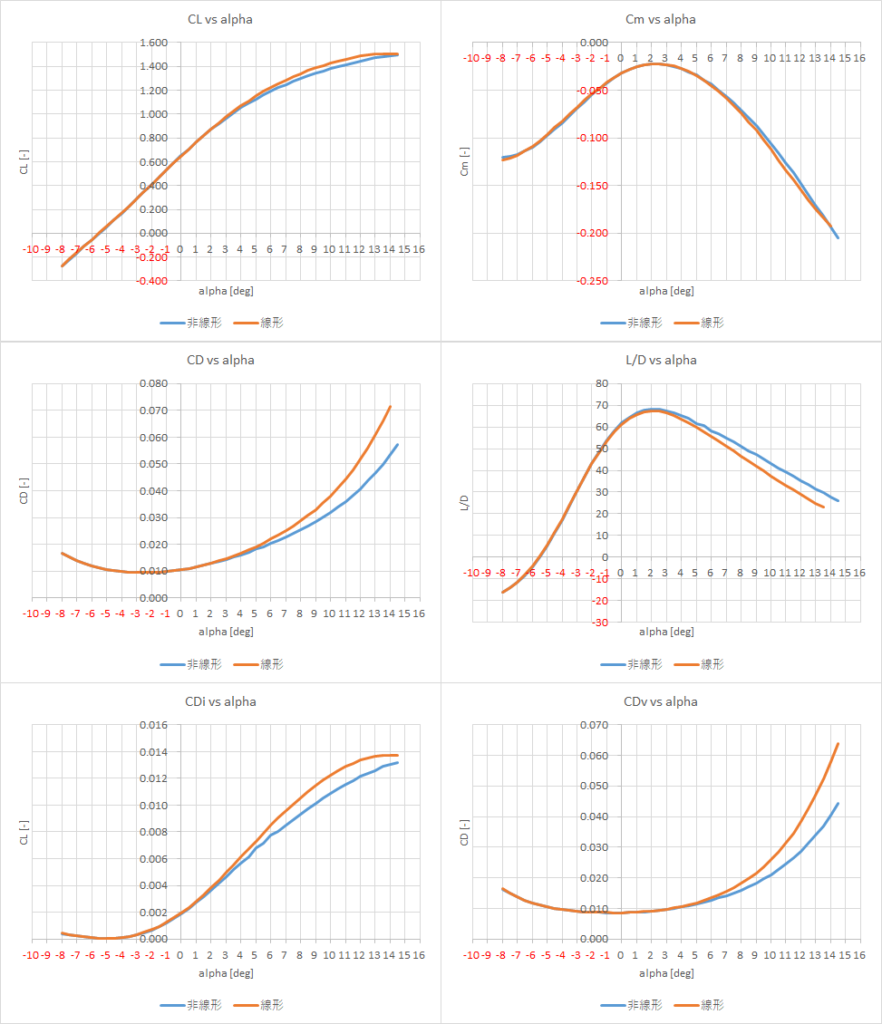
迎角の小さい範囲ではよく一致しているが,迎角が大きくなるにつれて線形解析での抗力が大きくなってしまっている.
原因を探るために,迎角15度での計算結果を比較した図を以下に示す
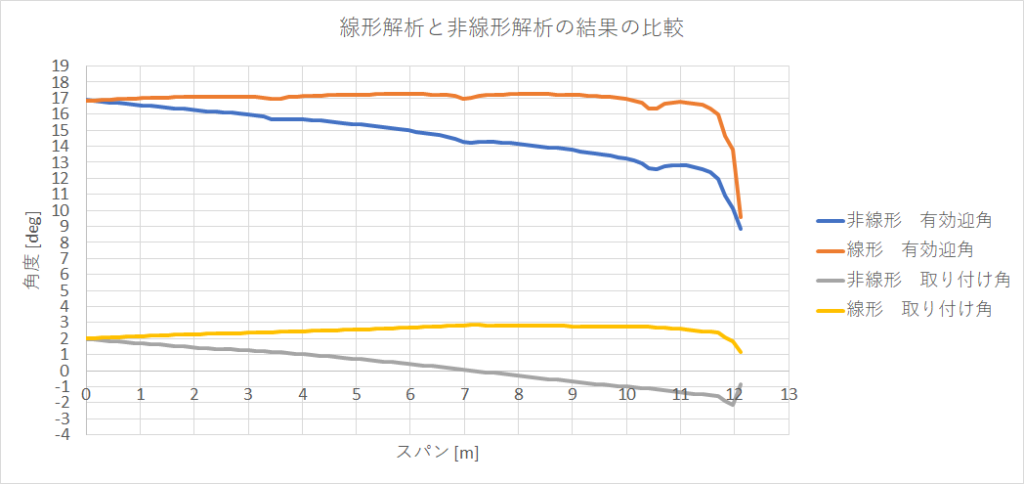
取り付け角を見てみると,線形解析では翼端に行くにしたがって取り付け角が大きくなっている(=ねじりあがっている)ことがわかる
なぜこのような結果になったかというと,線形解析の1回目の計算では下の図で示すように,二次元翼型のCmはほとんど0に近く,大きな\(C_{l}\)と空力中心-桁中心間の距離の分だけねじり上げのモーメントが生じ,桁がねじりあがってしまうからである
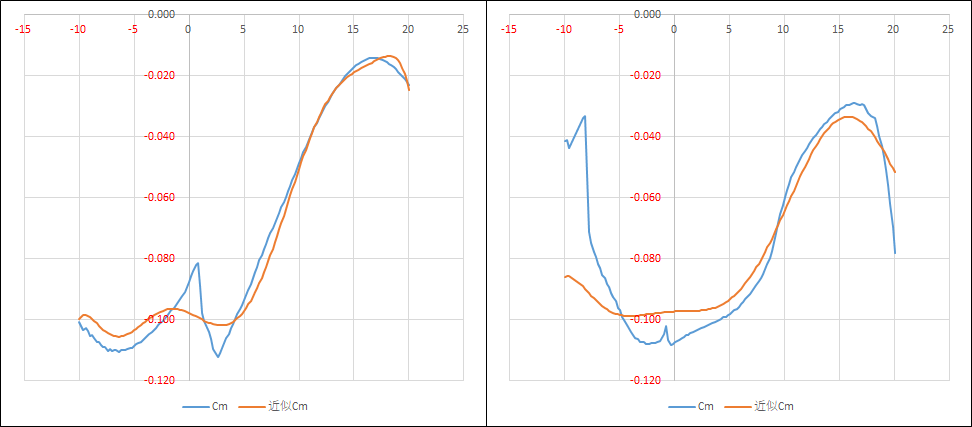
桁がねじりあがったことで有効迎角も大きくなり,結果として\(C_{D}\)の値が大きくなってしまう
そこで,線形解析の反復計算を2回から3回にして計算を行った結果を以下に示す
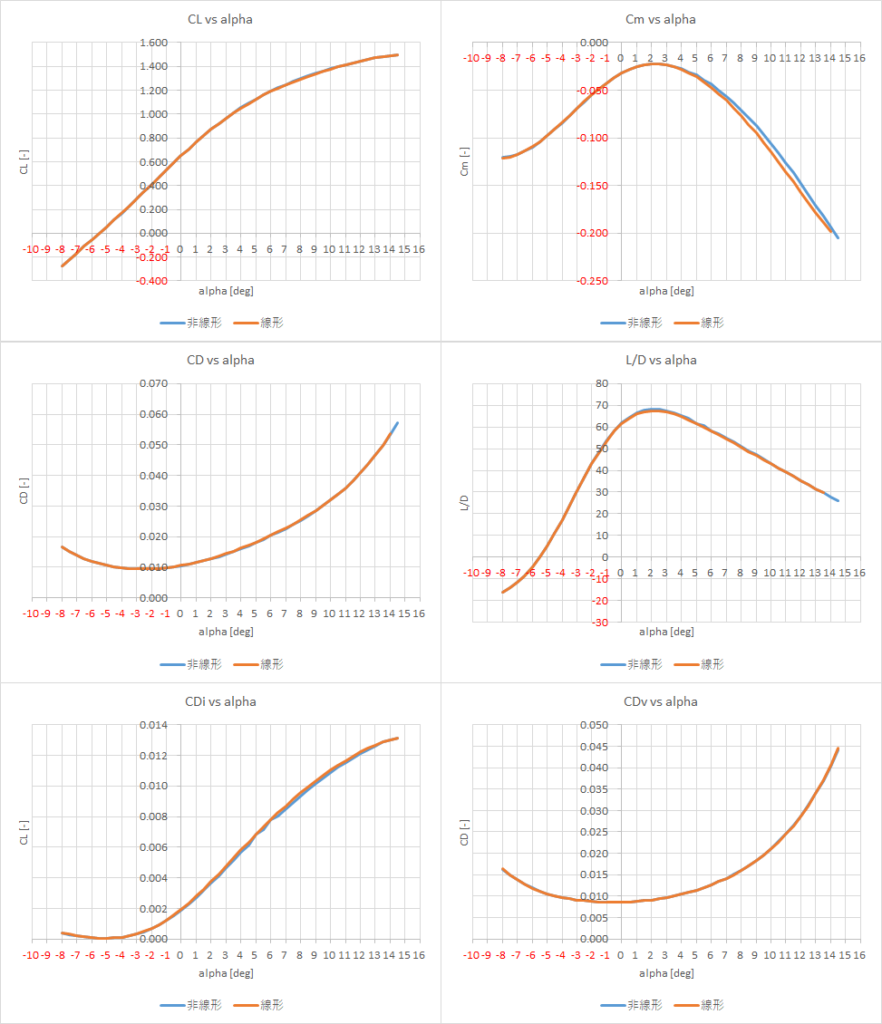
なんかもう非線形解析の意味がないくらいに一致するようになった
ちなみに「線形解析なのになんで失速してんの?」と思った人のために解説しておく
論文に書いてある線形解析では,誘導速度がないときの局所揚力係数\(C_{l_{0}}(i)\)をゼロ揚力角\(\alpha_{0}\)を使って次のように計算している
\begin{eqnarray}
C_{l_{0}}(i) &=& a_{0}(\alpha(i)-\alpha_{0}(i))
\end{eqnarray}
循環分布を求めるための局所揚力係数を線形近似しているので,計算結果でも失速はしなくなる
それに対して,今回のプログラムでは循環を求めるための局所揚力係数\(C_{l_{0}}(i)\)を二次元翼の\(C_{l}\)の多項式近似より求めている(=失速が考慮されている)ため,計算結果でも失速を考慮できている
この違いが今回のプログラムが線形解析なのに失速を計算できている理由である(※正しいかどうかはわからない)
まとめ
線形解析を行えば時間短縮になる
↓記事一覧
【追記】20200911
主翼の空力および構造計算のプログラムで宣言した変数に加えて,以下の変数を宣言する必要がある
Dim matrix1() As Double
Dim matrix2() As Double
Dim answer() As Doubleまた,繰り返しの計算回数を変更しておく
Dim iteration_max As Integer: iteration_max = 2【ミス修正】20210602
- 横・方向の安定微係数の計算の仕方を修正
【ミス修正】20221226
(4),(5)の符号ミスを修正した





コメント