滑空機のポーラーカーブを描くプログラムを製作する
目的
今回の目的は,設計した機体のポーラーカーブを描くプログラムを製作することである
ポーラーカーブとは,横軸に進行方向の水平速度u [m/s],縦軸に沈下速度w [m/s]を取ったグラフで,グライダーの性能を表す曲線である
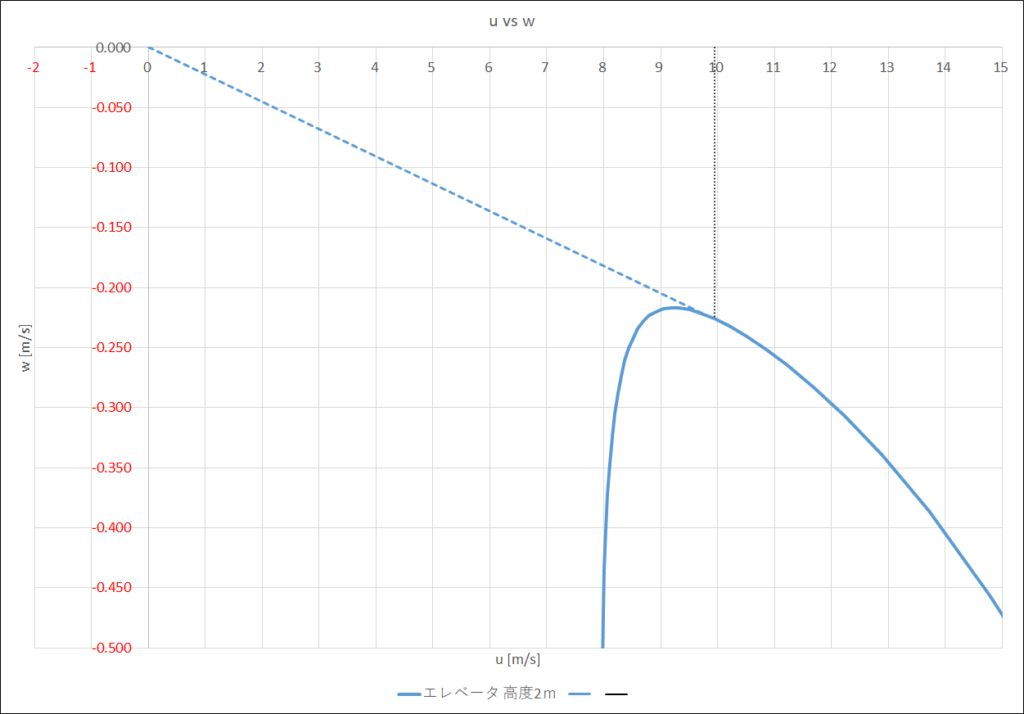
原点からポーラーカーブに接するように引いた直線は最良滑空角を表し,そのときの飛行速度を調べることができる
風(gust)がある場合は,その風に応じて原点をずらして接線を引けばよい(例えば背風2 [m/s]なら,(ug, wg)=(-2,0)の点からポーラーカーブに接線を引く)
下の図は,(ug, wg)=(-2, 0), (2, 0), (4, 0)のときの最良滑空角を示した図である
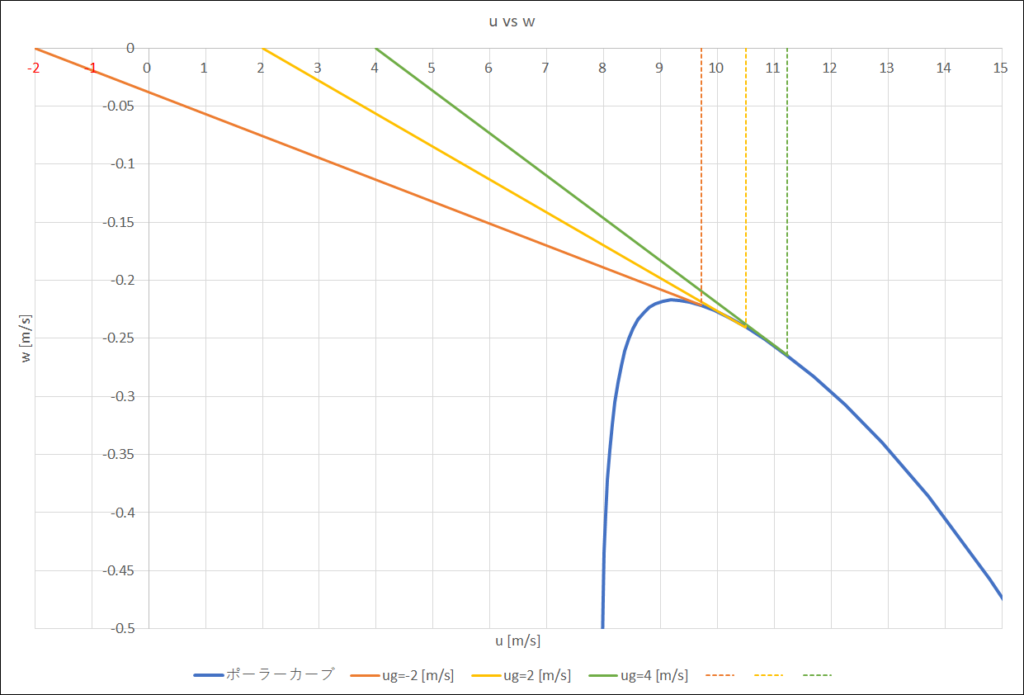
ug=-2 [m/s]のときは9.7 [m/s]で飛べば最良,ug=2 [m/s]のときは10.5 [m/s]で飛べば最良,ug=4 [m/s]のときは11.2 [m/s]で飛べば最良ということがわかる
これに基づいて,当日の風の状況に応じて機体の設定を変更すればより飛距離を稼ぐことが可能になる
フローチャート
プログラムのフローチャートを以下に示す
まず,速度に適当な初期値(最大速度)を設定し,各迎角のループに入る
ある迎角において全機計算を行い,CL<0だったらループを終了,CL>0だったらCmのループに入る
CL(>0)をもとに対気速度を計算し,再び全機計算を行う.Cmが0になるよう重心位置,もしくはエレベータ舵角を計算し,Cmが閾値以下になるまで繰り返し全機計算を行う(この繰り返し計算の仮定でもしCL<0になったらCmのループを抜け,次の迎角へ移行する)
Cmのループを抜けたら値を出力用配列に計算結果を格納し,次の迎角のループに入る
これをあらかじめ設定した迎角の範囲で計算し,結果を出力する
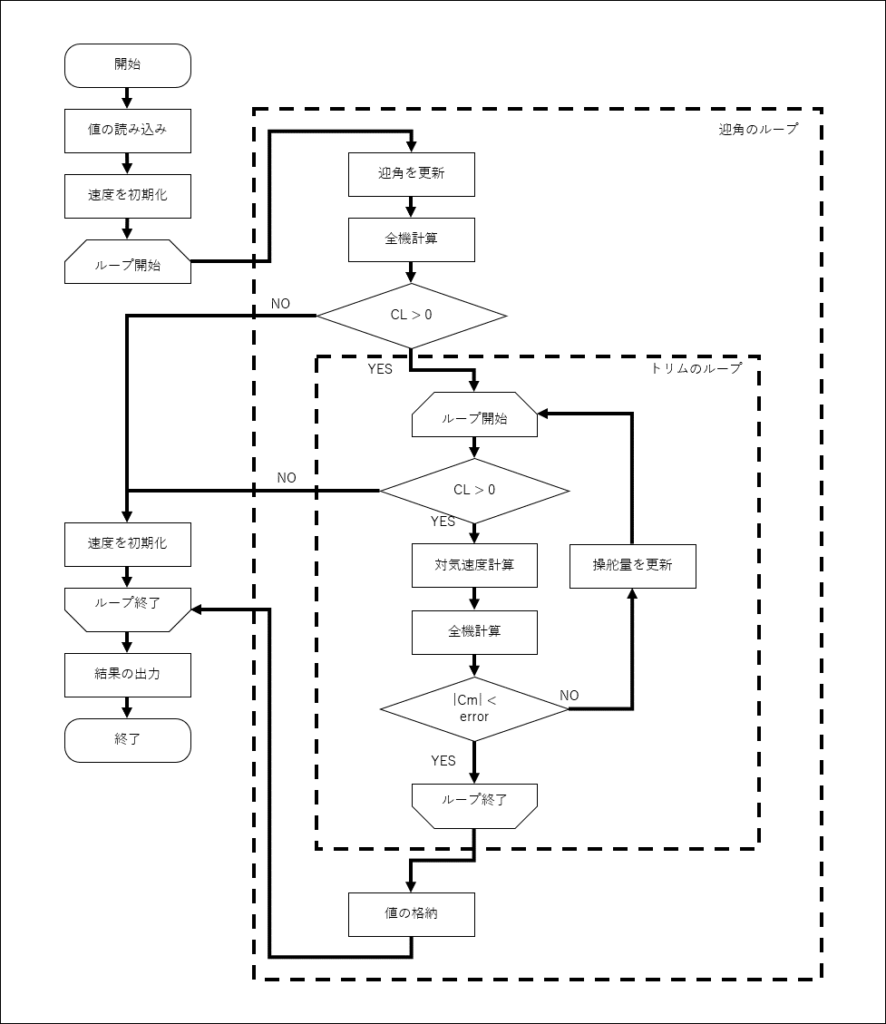
このフローチャートがわかりやすいかどうかはさておき,全機計算には線形解析を用いる
プログラムの解説
実際のプログラムを以下に示す
Sub 全機ポーラー解析()
'定数
Const a_min As Double = -10 '[deg]
Const a_max As Double = 20 '[deg]
Const da As Double = 0.5 '[deg]
Const V_max As Double = 15 '[m/s]
Const error As Double = 0.0005 '[-]
state = ReadState(state, 8) '状態変数の読み込み
data = (a_max - a_min) / da 'データ数の計算と出力用配列の大きさの宣言
state.Vair = V_max '速度を最大に設定
ReDim output(data, 10)
For i = 0 To data '迎角のループ
state.alpha = a_min + da * i '迎角の変更
Plane = 線形Plane_calculation(0, Plane, state) '全機計算
If Plane.CL < 0 Then state.Vair = V_max: GoTo continue '揚力係数が負だったらループを飛ばす
For j = 0 To 2 ^ 15 - 2 'Cmのループ
If Plane.CL < 0 Then state.Vair = V_max: GoTo continue '揚力係数が負になったらループを飛ばす
state.Vair = Sqr((2 * Weight) / (state.rho * Plane.S * Plane.CL)) '対気速度計算
Plane = 線形Plane_calculation(0, Plane, state) '全機計算
If Abs(Plane.Cm_cg) < error Then Plane.Cm_cg = 0: Exit For '収束判定
If sht9.Range("AR42") = "重心移動" Then
delta = (Plane.Cm_cg / Plane.CL) 'さらなる重心移動量を計算
state.dh = state.dh + delta '重心移動量を更新
Else
delta = -(Plane.Cm_cg / Cm_de) 'さらなるエレベータ舵角を計算
state.de = state.de + delta 'エレベータ舵角を更新
End If
Next j
With Plane '値の格納
output(num, 0) = state.alpha
output(num, 1) = state.Vair
output(num, 2) = .CL
output(num, 3) = .CD
output(num, 4) = .Cm_cg
output(num, 5) = -deg * (Atn(1 / .L_D))
output(num, 6) = state.Vair * Cos((-Atn(1 / .L_D)))
output(num, 7) = state.Vair * Sin((-Atn(1 / .L_D)))
output(num, 8) = state.de
output(num, 9) = state.dh
output(num, 10) = .L_D
End With
num = num + 1
continue:
Next i
sht9.Range(sht9.Range("AP49:AZ49"), sht9.Range("AP49:AZ49").End(xlDown)).ClearContents '前回のデータを消去
sht9.Range(sht9.Cells(49, 42), sht9.Cells(49 + num - 1, 52)) = output() '結果の表示
End Subループを飛ばす処理にはGoToステートメントを用いた
重心移動による\(C_{m}\)の変化を表す\(C_{m_{\delta h}}\),エレベータ舵角による\(C_{m}\)の変化を表す\(C_{m_{\delta e}}\)は次の式で表される
\begin{eqnarray}
C_{m_{\delta h}} &=& \frac{\partial}{\partial \delta h}(\frac{L\times (c_{mac}\delta h)}{\frac{1}{2}\rho V^{2} S c_{mac}})
=\frac{\partial}{\partial \delta h}(C_{L}\delta h)=C_{L} \\
C_{m_{\delta e}} &=& -V_{H}^{*}a_{t}\tau
\tag{航空機力学入門(4.43)}
\end{eqnarray}
\(\Delta C_{m}\)を0にするために必要な操舵量\(\Delta h\),\(\Delta e\)は次の式で計算できる
\begin{eqnarray}
\Delta h &=& \frac{\Delta C_{m}}{C_{m_{\delta h}}} \\
\Delta e &=& \frac{\Delta C_{m}}{C_{m_{\delta e}}}
\end{eqnarray}
プログラムの実行
実際にプログラムを実行してみる
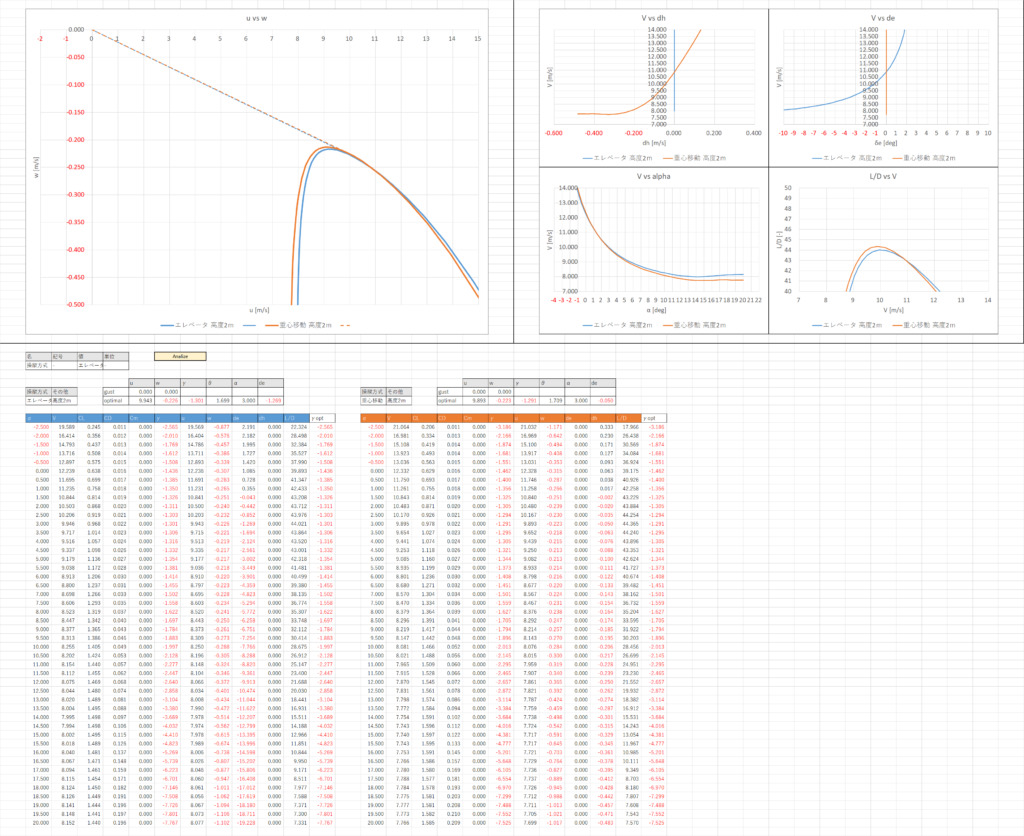
ポーラーカーブの接線を引く
まず,γgustの列で,各迎角における(u, v)と(ug, wg)の直線の傾き(経路角)[deg]を計算する
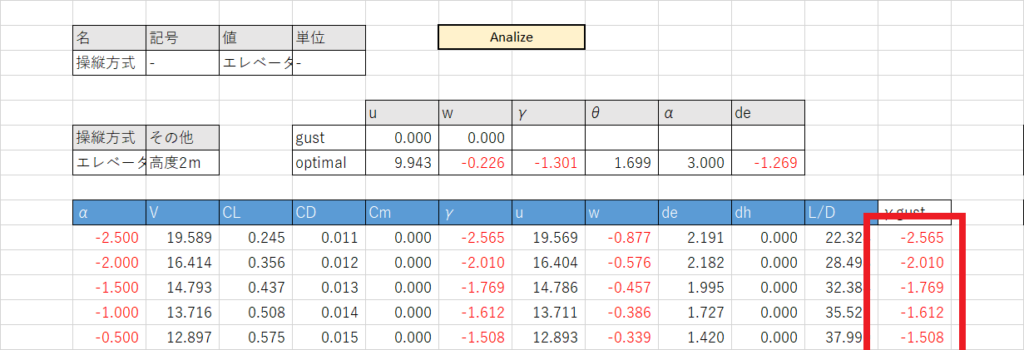
γoptimalのセルでMAX関数を使いγgustの最大値を表示する
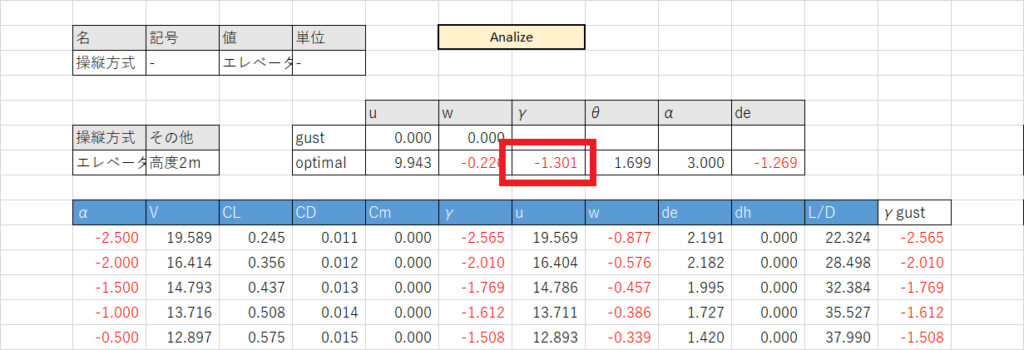
u_optimal,w_optimal,α_optimal,de_optimalのセルで,γgustが最大になるときのu,w,α,deの値を表示する(≫エクセル INDEX と MATCH 関数を組み合わせて VLOOKUP 関数より高度に検索する)
これで記事の最初に紹介したような図が描ける
まとめ
このポーラーカーブを使うにあたって注意してほしいのは,対称翼を参考に迎角が大きくなるにつれてカウルの抗力を大きくしているという点である
実際は対称翼よりもカウルのほうが迎角に対する抗力の上昇は大きいと思われるので,このポーラカーブでは高迎角時の性能を過大評価していることになる
容量用法に注意して活用していきたい
↓記事一覧




コメント