OpenFOAMで実装されている離散化スキームである linearUpwind について解説する
有限体積法による離散化
コンピュータで偏微分方程式を解くためには,計算格子上に偏微分方程式を離散化する必要がある
OpenFOAMで用いられている離散化手法である有限体積法を用いると,輸送方程式,発散,勾配は次のように離散化できる
(輸送方程式)
\begin{align}
&\frac{\partial}{\partial t}(\rho\phi)
+\nabla\cdot(\rho\mathbf{u}\phi)
=s
+\nabla\cdot\left(\Gamma\nabla \phi\right) \\
\\ \rightarrow \quad
&\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f}}
=s_{_{P}}V_{_{P}}
+\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{|\mathbf{x}_{_{N}}-\mathbf{x}_{_{P}}|}}
\end{align}
(発散)
\begin{equation}
\nabla\cdot\phi \quad \rightarrow \quad \sum_{f}\mathbf{S}_{f}\cdot\phi_{f}
\end{equation}
(勾配)
\begin{equation}
\nabla\phi \quad \rightarrow \quad \sum_{f}\mathbf{S}_{f}\phi_{f}
\end{equation}
ここで,添え字\(_P\),\(_N\),\(_f\) はそれぞれ注目セル\(P\),隣接セル\(N\),注目セルと隣接セルの境界面\(f\)における代表値であることを表し,\(\phi\)は何かしらの物理量,\(V\)はセル体積,\(\Gamma\)は拡散係数である
また,\(|S_{f}|\)は注目セルと隣接セルの境界面の面積,\(\mathbf{S}_{f}\)は境界面に垂直で境界面の面積\(|S_{f}|\)を大きさに持つ法線ベクトルであり,\(\sum_{f}\)はセルがもつすべての面に対する総和を表す
上記3つの離散化を見てみると未知数は\(\phi_{f}\)のみであり,有限体積法の離散化は「境界面上の代表値\(\phi_{f}\)をどのように補間するか」という点に集約されていることがわかる
セルが不規則に配置されている非構造格子では,\(\phi_{f}\)の離散化に使える値は注目セル\(P\)の代表値\(\phi_{_{P}}\)と隣接セル\(N\)の代表値\(\phi_{_{N}}\)の2つのみである
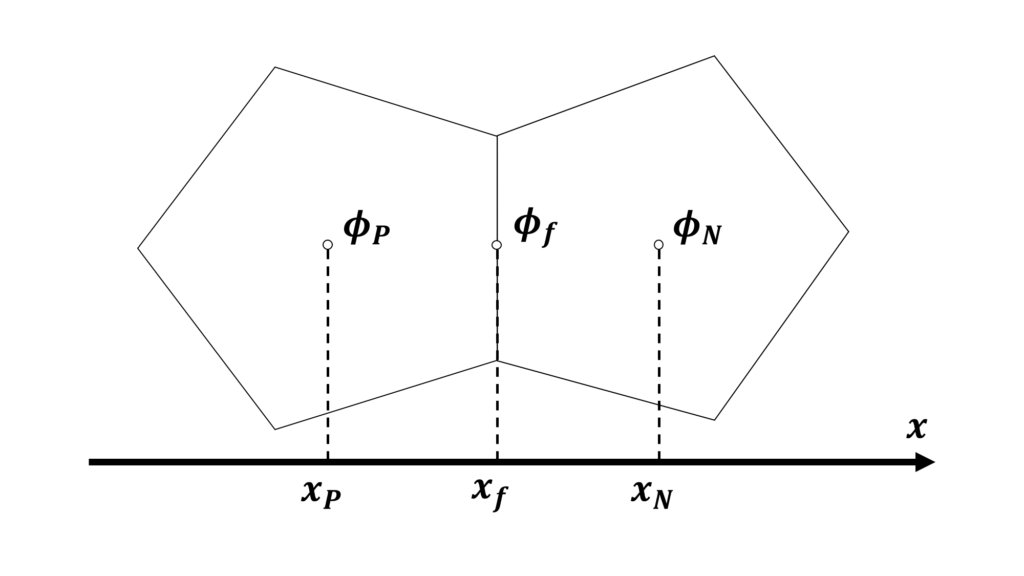
\(\phi_{f}\)を\(\phi_{_P}\)と\(\phi_{_N}\)によって補間すると次の連立方程式が得られる
\begin{equation}
\mathbf{A}_{_{P}}\phi_{_{P}}+\sum{\mathbf{A}_{_N}\phi_{_N}}
=\mathbf{b}
\end{equation}
\(\mathbf{A}\)や\(\mathbf{b}\)の具体的な値を決定するのは偏微分方程式の離散化に用いられた離散化スキームであり,離散化スキームの精度や性質によって計算の安定性や結果の精度は大きく変化する
↓離散化の導出についてはこちら
線形風上差分
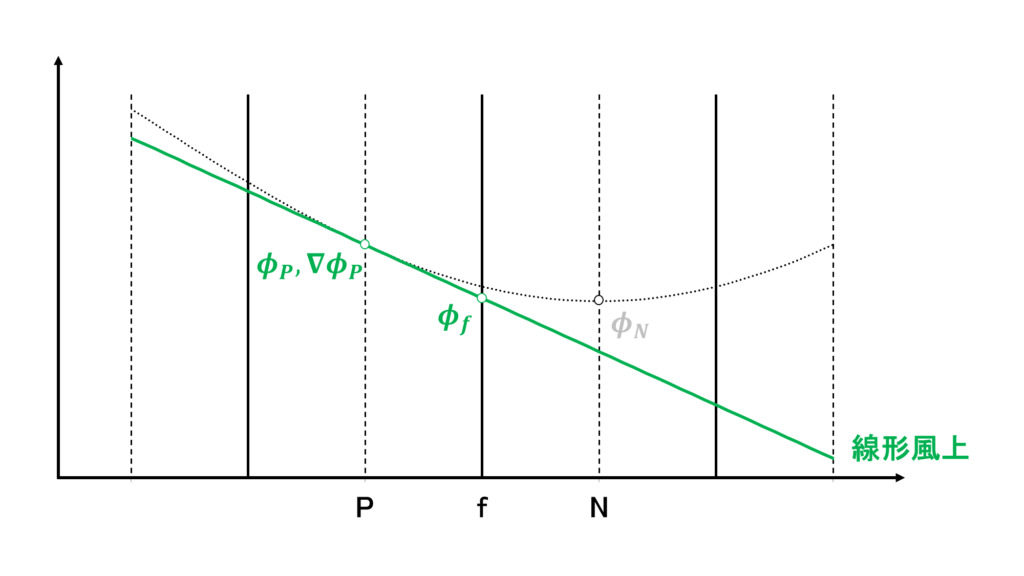
線形風上差分(linear upwind difference:LUD)は2次精度であり,1次風上差分(upwind)よりは数値粘性が大きくないので,計算が難しい複雑な流れ場をRANSで計算するときに,速度の対流項などに設定する
線形風上差分では,質量流束\(F=\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断し,上流側の値とその点における勾配を使って\(\phi_{f}\)を次のように線形補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\phi_{_{P}}+\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{P}\right) & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\phi_{_{N}}+\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{N}\right) & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
↓詳しくはこちら
OpenFOAMにおける実装
OpenFOAMでは,線形風上差分は以下のように実装される
\begin{align}
&\phi_{f}=\phi_{_{UD}}+\phi_{corr.} \tag{1} \\ \\
&\phi_{corr.}=\left\{\begin{array}{ll}
\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{P}\right)
& \left(F>0\right) \\
\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{N}\right)
& \left(F<0\right) \\
\end{array}\right. \tag{2}
\end{align}
\(\phi_{_{UD}}\)は風上差分(upwind)を用いた場合の境界面の値であり,\(\phi_{corr.}\)は線形補完を行うための補正項である
参考
≫User Guide: Linear-upwind divergence scheme - OpenFOAM
実装は主に以下のファイルに記述されている
≫surfaceInterpolationScheme.C:離散化スキームの親クラス
≫linearUpwind.H:upwind を継承した子クラス
surfaceInterpolationScheme.C で風上差分(upwind)に補正項が追加され,linearUpwind.H で補正項\(\phi_{corr.}\)が定義されている
↓upwind についてはこちら
それでは確認していく
補正項
補正項\(\phi_{corr.}\)は linearUpwind.C の correction() で次のように定義されている
\begin{equation}
\phi_{corr.}=\left\{\begin{array}{ll}
\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{P}\right)
& \left(F>0\right) \\
\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{N}\right)
& \left(F<0\right) \\
\end{array}\right. \tag{2}
\end{equation}
プログラムでは \(\mathrm{vf}=\phi\),\(\mathrm{tsfCorr}=\phi_{corr.}\),\(\mathrm{faceFlux}=F\),\(\mathrm{Cf}=\mathbf{x}_{f}\),\(\mathrm{C}=\mathbf{x}\) という変数が用いられている
const fvMesh& mesh = this->mesh();
tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> tsfCorr // 補正項を入れるための変数
(
new GeometricField<Type, fvsPatchField, surfaceMesh>
(
IOobject
(
"linearUpwind::correction(" + vf.name() + ')',
mesh.time().timeName(),
mesh,
IOobject::NO_READ,
IOobject::NO_WRITE,
false
),
mesh,
dimensioned<Type>(vf.name(), vf.dimensions(), Zero)
)
);
GeometricField<Type, fvsPatchField, surfaceMesh>& sfCorr = tsfCorr.ref();
const surfaceScalarField& faceFlux = this->faceFlux_; // 質量流束
const labelList& owner = mesh.owner(); // 注目セルのインデックス
const labelList& neighbour = mesh.neighbour(); // 隣接セルのインデックス
const volVectorField& C = mesh.C(); // 注目セルを代表する点の座標
const surfaceVectorField& Cf = mesh.Cf(); // 境界面を代表する点の座標
tmp<fv::gradScheme<scalar>> gradScheme_ // 勾配を計算する離散化スキーム
(
fv::gradScheme<scalar>::New
(
mesh,
mesh.gradScheme(gradSchemeName_)
)
);
for (direction cmpt = 0; cmpt < pTraits<Type>::nComponents; cmpt++)
{
tmp<volVectorField> tgradVf =
gradScheme_().grad(vf.component(cmpt), gradSchemeName_);
const volVectorField& gradVf = tgradVf(); // 勾配
forAll(faceFlux, facei)
{
const label celli =
(faceFlux[facei] > 0) ? owner[facei] : neighbour[facei]; // 風上側のセルのインデックス
setComponent(sfCorr[facei], cmpt) =
(Cf[facei] - C[celli]) & gradVf[celli]; // 補正項の計算
}
:
}
return tsfCorr;correction() は surfaceInterpolationScheme.H で次のように定義されている
//- Return the explicit correction to the face-interpolate
// for the given field
virtual tmp<GeometricField<Type, fvsPatchField, surfaceMesh>>
correction(const GeometricField<Type, fvPatchField, volMesh>&) const
{
return tmp<GeometricField<Type, fvsPatchField, surfaceMesh>>
(
nullptr
);
}
補正項の追加
補正項の追加は surfaceInterpolationScheme.C の interpolate() で次のように定義されている
\begin{equation}
\phi_{f}=\phi_{_{UD}}+\phi_{corr.} \tag{1}
\end{equation}
tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> tsf
= interpolate(vf, weights(vf)); // upwindによる境界面上の補間値
if (corrected())
{
tsf.ref() += correction(vf); // 線形風上差分の補正項を追加
}
return tsf;interpolate() は surfaceInterpolationScheme.H で次のように定義されている
//- Return the face-interpolate of the given tmp cell field
// with explicit correction
tmp<GeometricField<Type, fvsPatchField, surfaceMesh>>
interpolate
(
const tmp<GeometricField<Type, fvPatchField, volMesh>>&
) const;
まとめ
OpenFOAMで実装されている離散化スキームである linearUpwind について解説した
↓その他の離散化スキーム
↓おすすめ記事

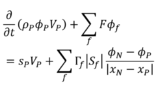






コメント