有限体積法における離散化スキームについての解説と導出を行う
keyword: 有限体積法,数値粘性,中心差分,風上差分,QUICK
有限体積法を用いた離散化
コンピュータで偏微分方程式を解くためには,計算格子上に偏微分方程式を離散化する必要がある
離散化手法の1つである有限体積法は次のような特徴を持つ
- 積分型の流れの方程式を基礎とする
- 速度や圧力などの物理量は検査体積(セル)の代表値を求める
- 質量や運動量などの保存則はセルの境界からの流入/流出およびセル内部での発生/消滅によって表す
- 非構造格子を用いる
セルが不規則に配置されている非構造格子では,離散化に使える値は注目セル\(P\)の代表値\(\phi_{_{P}}\)と隣接セル\(N\)の代表値\(\phi_{_{N}}\)の2つのみである
2つのセルの間にある境界面\(f\)の代表値\(\phi_{f}\)は\(\phi_{_{P}}\)と\(\phi_{_{N}}\)を用いた補間によって求められる
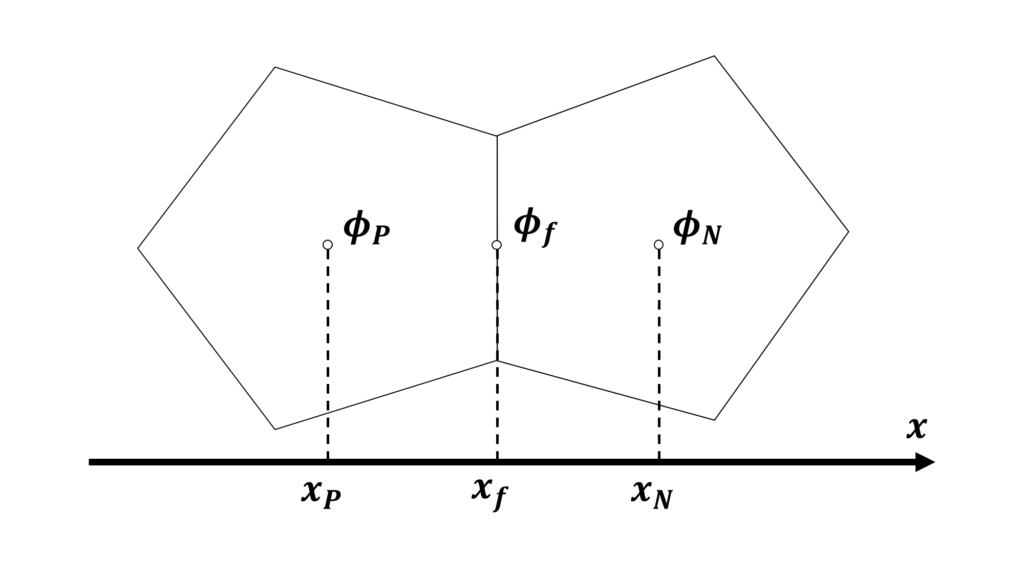
一般的な輸送方程式に対する離散化
一般に,物理量\(\phi\)の輸送方程式は時間項,対流項,粘性項,ソース項(生成項+散逸項)から構成され,次のようにあらわされる
\begin{equation}
\frac{\partial}{\partial t}(\rho\phi)
+\nabla\cdot(\rho\mathbf{u}\phi)
=s
+\nabla\cdot\left(\Gamma\nabla \phi\right)
\end{equation}
ここで,
- \(\phi=\mathbf{u}\),\(\Gamma=\mu+\mu_{t}\),\(s=-\frac{\partial p}{\partial x}\)とすればNavier-Stokes方程式
- \(\phi=k\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{k}}\),\(s=P_{k}-\varepsilon\)とすれば標準k-εモデルの\(k\)の輸送方程式,
- \(\phi=\varepsilon\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\),\(s=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}\)とすれば標準k-εモデルの\(\varepsilon\)の輸送方程式
である
上記の輸送方程式をセル体積で積分し,離散化すると次のようになる
\begin{equation}
\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f}}
=s_{_{P}}V_{_{P}}
+\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{|\mathbf{x}_{_{N}}-\mathbf{x}_{_{P}}|}}
\end{equation}
また,\(\phi\)の発散と勾配を有限体積法で離散化すると次のようになる
\begin{align}
\nabla\cdot\phi \quad &\rightarrow \quad \sum_{f}\mathbf{S}_{f}\cdot\phi_{f} \\ \\
\nabla\phi \quad &\rightarrow \quad \sum_{f}\mathbf{S}_{f}\phi_{f} \\
\end{align}
ここで,\(V_{_{P}}\)はセル体積,\(|S_{f}|\)は注目セルと隣接セルの境界面の面積,\(\mathbf{S}_{f}\)は境界面に垂直で境界面の面積\(|S_{f}|\)を大きさに持つ法線ベクトルであり,\(\sum_{f}\)はセルがもつすべての面に対する総和を表す
上記3つの離散化を見てみると未知数は\(\phi_{f}\)のみであり,有限体積法の離散化は「境界面上の代表値\(\phi_{f}\)をどのように補間するか」という点に集約されていることがわかる
\(\phi_{f}\)を\(\phi_{_P}\)と\(\phi_{_N}\)によって補間すると次の連立方程式が得られる
\begin{equation}
\mathbf{A}_{_{P}}\phi_{_{P}}+\sum{\mathbf{A}_{_N}\phi_{_N}}
=\mathbf{b}
\end{equation}
\(\mathbf{A}\)や\(\mathbf{b}\)の具体的な値を決定するのは偏微分方程式の離散化に用いられた離散化スキームであり,離散化スキームの精度や性質によって計算の安定性や結果の精度は大きく変化する
↓導出についてはこちら
非構造格子で離散化に使える値は,注目セル\(P\)の代表値\(\phi_{_{P}}\)と隣接セル\(N\)の代表値\(\phi_{_{N}}\)の2つのみである
有限体積法による離散化は「境界面上の代表値\(\phi_{f}\)をどのように補間するか」という点に集約されている
離散化方程式の係数行列の値は離散化に用いられる離散化スキームによって決まる
離散化の種類と精度
離散化の種類
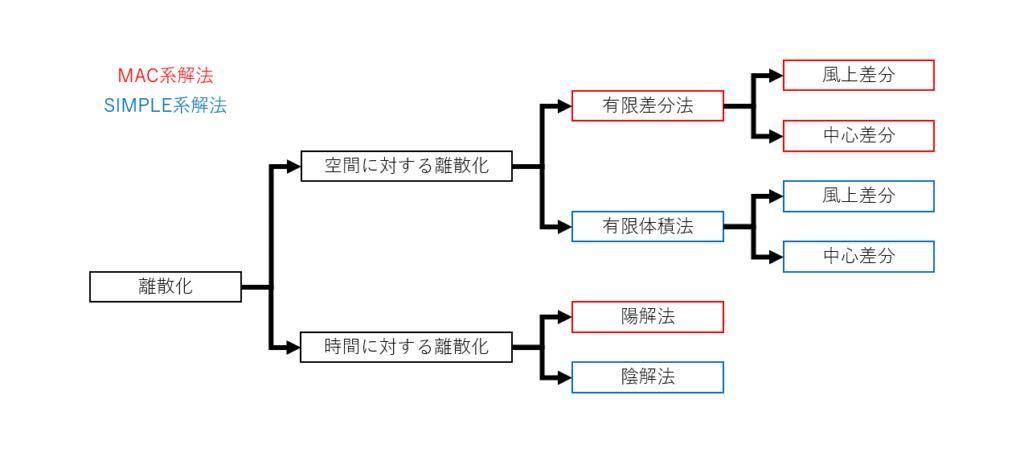
偏微分方程式の離散化は,「空間に対する離散化」と「時間に対する離散化」の2つに分けられる
空間に対する離散化の手法には有限差分法や有限体積法などがあり,それぞれにおいて中心差分と風上差分が存在する
時間に対する離散化の手法には陽解法と陰解法があり,陽解法は有限差分法を用いるMAC系の解法に,陰解法は有限体積法を用いるSIMPLE系の解法に用いられる
離散化の精度
次のような格子幅\(\Delta x\)の1次元の計算格子を考える
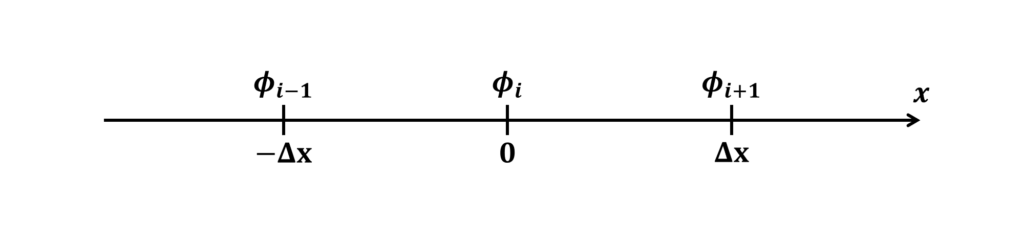
ここで,\(\phi_{i}\)に対する風上差分による補間\(\phi_{i_{_{UD}}}\)と中心差分による補間\(\phi_{i_{_{CD}}}\)はテイラー展開によって次の式で表される
\begin{align}
&\phi_{i_{_{UD}}}=\phi_{i-1}+\frac{\partial \phi_{i}}{\partial x}\Delta x+\cdots \\ \\
&\phi_{i_{_{CD}}}=\frac{\phi_{i-1}+\phi_{i+1}}{2}-\frac{1}{2}\frac{\partial^{2} \phi_{i}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\end{align}
上記の式で,\(\Delta x\)を含む項は離散化に伴う誤差であり,計算格子を極限まで細かくしていけば \(\Delta x=0\)となり,誤差も0になる
離散化式のテイラー展開で出てくる項が計算格子幅(もしくは時間ステップ)のn乗に比例しているとき,その離散化スキームは「n次精度」であるという
離散化には空間に対する離散化と時間に対する離散化がある
空間に対する離散化手法には有限差分法と有限体積法があり,時間に対する離散化手法には陽解法と陰解法がある
離散化に伴う誤差が計算格子幅や時間ステップ幅のn乗に比例するとき,n次精度の離散化スキームであるという
今回の記事では,有限体積法の離散化として中心差分,風上差分,線形風上差分,QUICKを説明し,時間発展の陰解法としてオイラー法と後退差分について説明する
中心差分
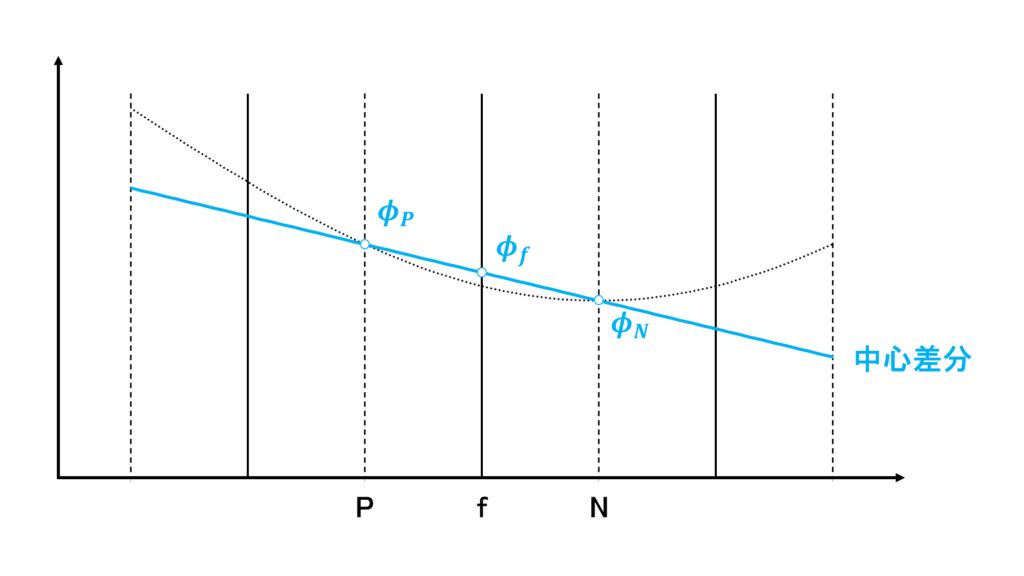
中心差分(central difference:CD)では,\(\phi_{f}\)を次のように補完する
\begin{equation}
\phi_{f}=w\phi_{_{P}}+\left(1-w\right)\phi_{_{N}}, \qquad
w=\frac{\left|\mathbf{x}_{f}-\mathbf{x}_{_{N}}\right|}{\left|\mathbf{x}_{_{P}}-\mathbf{x}_{_{N}}\right|}
\end{equation}
中心差分は2次精度であり,対流項,発散,勾配,すべてに使用できる有限体積法で最もポピュラーな離散化スキームである
離散化スキームについてよくわからないならとりあえずこれを設定しておけばいい
導出
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{f}\)に原点をとり,\(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\left|\mathbf{x}_{f}-\mathbf{x}_{_{_N}}\right|=\Delta x\) とすると,\(\phi_{f}=\phi(0)\),\(\phi_{_{P}}=\phi(-\Delta x)\),\(\phi_{_N}=\phi(\Delta x)\) なので
\begin{align}
\phi_{_{P}}=\phi_{f}-\frac{\partial \phi_{f}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\tag{i} \\ \\
\phi_{_N}=\phi_{f}+\frac{\partial \phi_{f}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\tag{ii} \\ \\
\end{align}
(i)+(ii)より,中心差分の式が求められ,2次精度であることがわかる
\begin{align}
\phi_{f}=\frac{\phi_{_P}+\phi_{_N}}{2}-\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\end{align}
風上差分
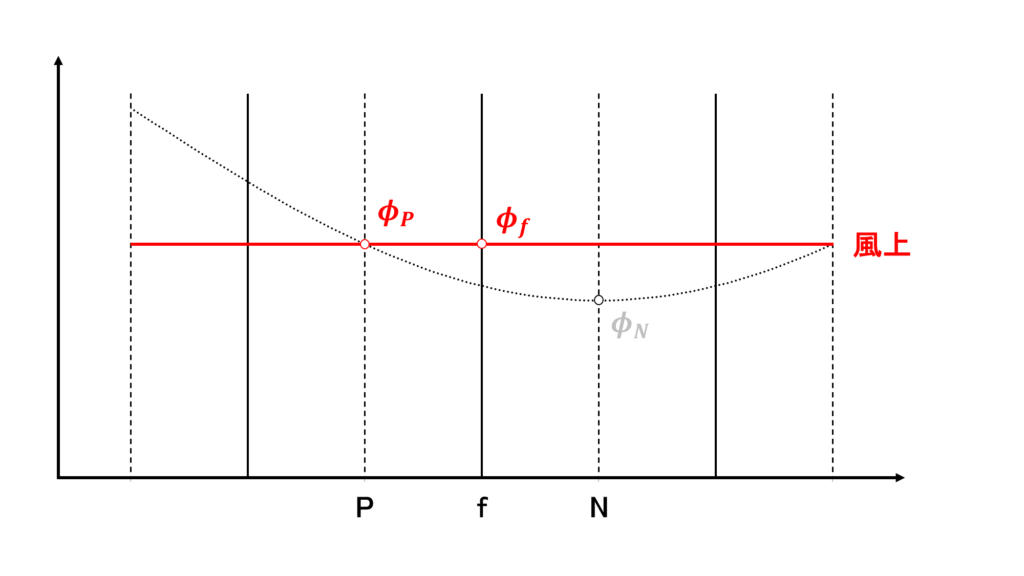
風上差分(upwind difference:UD)では,上流側の値をそのまま持ってくることによって\(\phi_{f}\)を次のように補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\phi_{_{P}} & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\phi_{_{N}} & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
質量流束\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断している
風上差分は1次精度であり,数値粘性が非常に大きく,計算の安定性は大きく向上するが計算結果の精度は非常に悪い
計算が難しい複雑な流れ場をRANSで計算するときに,速度の対流項に二次精度以上の風上差分を設定したうえで,\(k\)や\(\varepsilon\)の対流項に風上差分を設定するのはまだ許される
導出
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{f}\)に原点をとり,\(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\Delta x\) とすると,\(\phi_{f}=\phi(0)\),\(\phi_{_{P}}=\phi(-\Delta x)\) なので
\begin{align}
\phi_{_{P}}=\phi_{f}-\frac{\partial \phi_{f}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\tag{i}
\end{align}
\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\) とすると,(i)より風上差分の式が求まり,1次精度であることがわかる
\begin{align}
\phi_{f}=\phi_{_{P}}+\frac{\partial \phi_{f}}{\partial x}\Delta x
-\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\end{align}
線形風上差分
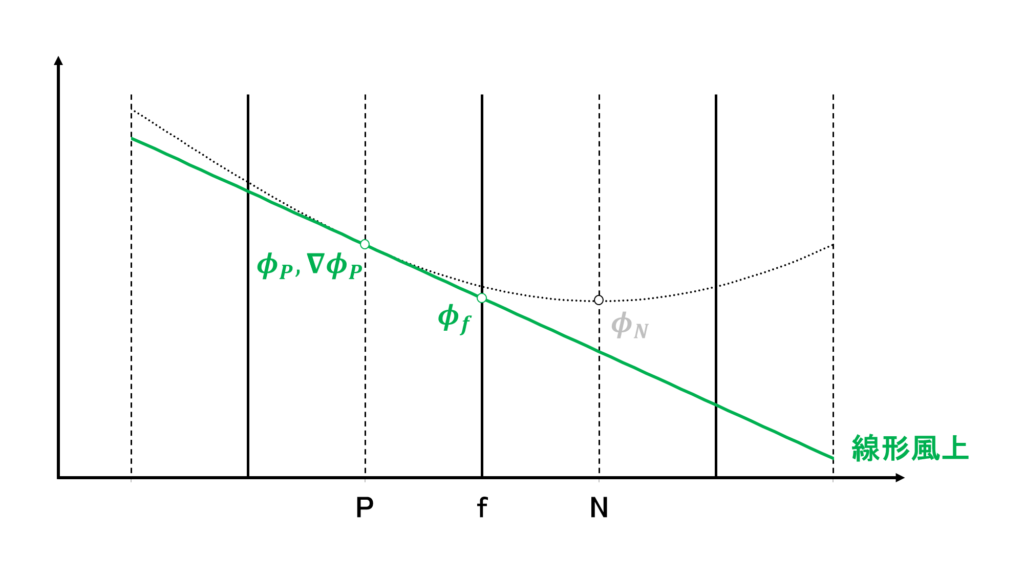
線形風上差分(linear upwind difference:LUD)では,上流側の値とその点における勾配を使って,\(\phi_{f}\)を次のように線形補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\phi_{_{P}}+\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{P}\right) & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\phi_{_{N}}+\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{N}\right) & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
質量流束\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断している
線形風上差分は2次精度であり,1次風上差分よりは数値粘性が大きくないので,計算が難しい複雑な流れ場をRANSで計算するときに,速度の対流項などに設定する
導出
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{P}\)に原点をとり,\(\Delta x=\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|\) とすると,\(\phi_{P}=\phi(0)\),\(\phi_{f}=\phi(\Delta x)\) なので
\begin{align}
\phi_{f}=\phi_{P}+\frac{\partial \phi_{P}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{P}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\tag{i}
\end{align}
(i)で二次以上の誤差を無視しすると,\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\) のときの線形風上差分の式が得られる
\begin{align}
\phi_{f}=\phi_{P}
+\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right)
\end{align}
QUICK
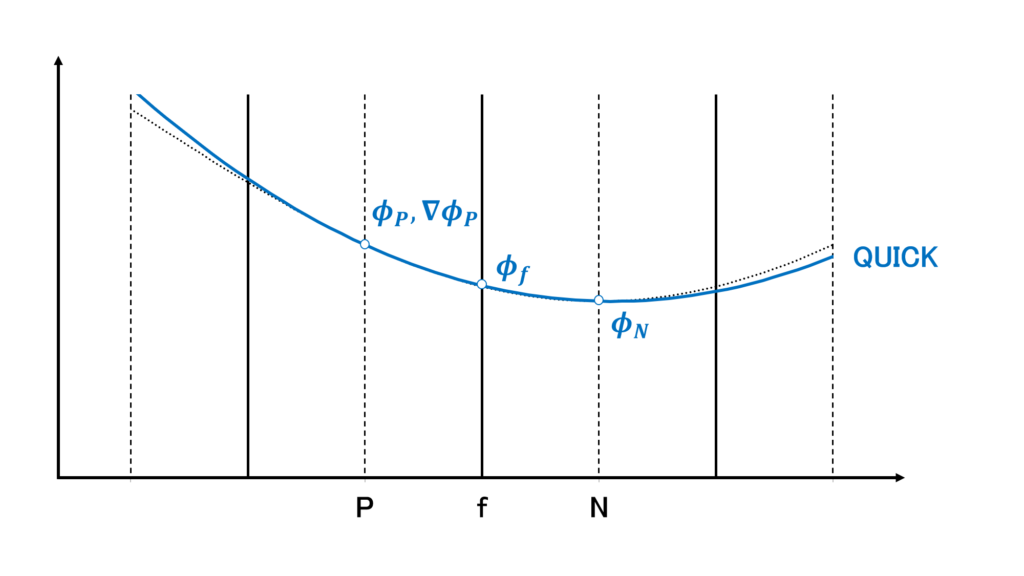
QUICK(Quadratic Upstream Interpolation for Convective Kinematics)では,上流側の値,上流側の点における勾配,下流側の値の3つを使って,\(\phi_{f}\)を次のように補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\frac{3}{4}\phi_{_{P}}+\frac{1}{4}\phi_{_{N}}
+\frac{1}{4}\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{N}-\mathbf{x}_{P}\right)
& \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\frac{1}{4}\phi_{_{P}}+\frac{3}{4}\phi_{_{N}}
+\frac{1}{4}\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{P}-\mathbf{x}_{N}\right)
& \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
質量流束\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断している
QUICKは補間としては3次精度であり,少しだけ数値粘性の力を借りたいときの速度の対流項としてよく設定される
導出
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{f}\)に原点をとり,上式の3次以上の誤差を無視して次のような2次式として考える
\begin{align}
&\phi(x)=a_{0}+a_{1} x+a_{2}x^{2} \\ \\
&\phi'(x)=a_{1}+2a_{2}x
\end{align}
簡単のため \(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\left|\mathbf{x}_{f}-\mathbf{x}_{_{N}}\right|=\Delta x\) であると仮定し,\(\phi(-\Delta x)=\phi_{_{P}}\),\(\phi(\Delta x)=\phi_{_{N}}\),\(\phi'(-\Delta x)=\phi'_{_{P}}\) という3つの関係式を考えることで \(\phi_{f}=\phi(0)=a_{0}\) を求める
\begin{align}
&\phi_{_P}=a_{0}-a_{1} \Delta x+a_{2}{\Delta x}^{2} \tag{i} \\
&\phi_{_N}=a_{0}+a_{1} \Delta x+a_{2}{\Delta x}^{2} \tag{ii} \\
&\phi'_{_P}=a_{1}-2a_{2}{\Delta x} \tag{iii} \\
\end{align}
(i)+(ii),(ii)-(i),(iii)より
\begin{align}
&a_{0}+a_{2}{\Delta x}^{2}=\frac{\phi_{_P}+\phi_{_N}}{2} \\
&2\Delta xa_{1}=\phi_{_N}-\phi_{_P} \\
&a_{1}-2a_{2}{\Delta x}=\phi'_{_P} \\
\end{align}
よって,
\begin{align}
&a_{0}=\frac{\phi_{_P}+\phi_{_N}}{2}+\frac{\phi'_{_P}}{2}\Delta x-\frac{\phi_{_N}-\phi_{_P}}{4} \\
&a_{1}=\frac{\phi_{_N}-\phi_{_P}}{2\Delta x} \\
&a_{2}=-\frac{\phi'_{_P}}{2\Delta x}+\frac{\phi_{_N}-\phi_{_P}}{(2\Delta x)^2} \\
\end{align}
\(\Delta x=\frac{\mathbf{x}_{_N}-\mathbf{x}_{_P}}{2}\)とすると,\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\) のときのQUICKの式が得られる
\begin{align}
&\phi_{f}=a_{0}=\frac{\phi_{_P}+\phi_{_N}}{2}+\frac{\phi'_{_P}}{2}\frac{\mathbf{x}_{_N}-\mathbf{x}_{_P}}{2}-\frac{\phi_{_N}-\phi_{_P}}{4} \\
\\ \rightarrow \quad
&\phi_{f}=\frac{3}{4}\phi_{_{P}}+\frac{1}{4}\phi_{_{N}}
+\frac{1}{4}\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{N}-\mathbf{x}_{P}\right)
\end{align}
参考
≫非構造型格子における離散化スキーム (PDFダウンロード)
陰解法
時間項の離散化手法には次のようなスキームがある
オイラー陰解法(Euler implicit)
\begin{equation}
\int_{V}{\frac{\partial}{\partial t}(\rho\phi)}dV
=\frac{(\rho_{_{P}}\phi_{_{P}}V_{_{P}})-(\rho_{_{P}}\phi_{_{P}}V_{_{P}})^{(n-1)}}{\Delta t}
\end{equation}
後退差分(Backward differencing)
\begin{equation}
\int_{V}{\frac{\partial}{\partial t}(\rho\phi)}dV
=\frac{3(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
-4(\rho_{_{P}}\phi_{_{P}}V_{_{P}})^{(n-1)}
+(\rho_{_{P}}\phi_{_{P}}V_{_{P}})^{(n-2)}}{2\Delta t}
\end{equation}
ここで,添え字\(^{(n-1)}\)は1つ前の時間ステップ,\(^{(n-2)}\)は2つ前の時間ステップにおける値を表し,\(\Delta t\)は時間刻み幅である
オイラー陰解法は1次精度,後退差分は2次精度である
陰解法では理論的にどんな大きさの時間刻みでも安定して計算できるが,時間刻みの大きさはクーラン数が1以下になるように設定するのが好ましい
参考
≫クーラン数と流体解析:初心者のための流体解析入門(7)- MONOist
導出
時刻\(t=t_{n}\)において,\(\phi(t_{n})=\phi\) についてテイラー展開を行うと次のようになる
\begin{equation}
\phi^{(n-1)}=\phi(t_{n}-\Delta t)=\phi-\frac{\partial \phi}{\partial t} \Delta t
+\frac{1}{2}\frac{\partial^{2} \phi}{\partial t^{2}}{\Delta t}^{2}
-\frac{1}{6}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots
\tag{i}
\end{equation}
\begin{equation}
\phi^{(n-2)}=\phi(t_{n}-2\Delta t)=\phi-2\frac{\partial \phi}{\partial t} \Delta t
+2\frac{\partial^{2} \phi}{\partial t^{2}}{\Delta t}^{2}
-\frac{4}{3}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots
\tag{ii}
\end{equation}
(i)より,オイラー陰解法は次の式で表される
\begin{equation}
\frac{\partial \phi}{\partial t}=\frac{\phi-\phi^{(n-1)}}{\Delta t}
+\frac{1}{2}\frac{\partial^{2} \phi}{\partial t^{2}}{\Delta t}
-\frac{1}{6}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots
\end{equation}
(i)×4-(ii)より,後退差分は次の式で表される
\begin{align}
&4\phi^{(n-1)}-\phi^{(n-2)}=3\phi-2\frac{\partial \phi}{\partial t} \Delta t
-\frac{2}{3}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots \\
\\ \rightarrow \quad
&\frac{\partial \phi}{\partial t}=\frac{3\phi-4\phi^{(n-1)}+\phi^{(n-2)}}{2 \Delta t}
-\frac{1}{3}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{2}+\cdots \\
\end{align}
まとめ
有限体積法における離散化スキームについての解説と導出を行った
離散化スキームの説明はだいたい有限差分法で行われているので,有限体積法の説明として参考になればと思う
↓おすすめ記事
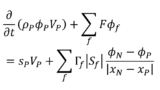


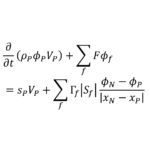

コメント