Smagorinskyモデルの導出とDynamicモデルの解説を行う
keyword:Smagorinskyモデル,Dynamic Smagorinskyモデル
Filtered Navier-Stokes方程式
LESの基礎方程式はフィルターを施した連続の式とNavier-Stokes方程式である
フィルターをかけた基礎方程式は次のように表される
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{_{SGS}}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
上式において,SGSの乱れの効果を表すSGS応力は渦粘性近似によって次のようにモデル化されている
\begin{equation}
\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}
=\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}
\end{equation}
\(\nu_{_{SGS}}\)はSGS渦粘性係数であり,\(\overline{S}_{ij}\)はひずみ速度テンソル \(\overline{S}_{ij}=\frac{1}{2}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\) である
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数はSGS渦粘性係数\(\nu_{_{SGS}}\)ただ1つであり,この\(\nu_{_{SGS}}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
Smagorinskyモデル
Smagorinskyモデルでは,SGS渦粘性係数は次の式で定義される
\begin{equation}
\nu_{_{SGS}}=\left(C_{s}f_{s}\Delta\right)^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\end{equation}
\(\Delta\)はフィルター幅であり,\(C_{s}\)はこのモデルで与える必要のある唯一のモデル定数でSmagorinsky定数とよばれる
\(f_{s}\)は壁面で滑りなし条件 \(\left.\nu_{_{SGS}}\right|_{wall}=0\)を与えるための減衰関数で,Van Driest関数が用いられる
\begin{equation}
f_{s}=1-\exp{\left(-\frac{y^{+}}{A^{+}}\right)}, \qquad A^{+} \simeq 25
\end{equation}
Smagorinsky定数の理論値は \(C_{s}=0.173\) であり,一様等方乱流では実験結果とよく一致することが確認されている
一方で,チャネル乱流などのせん断乱流に対してはより低い値 \(C_{s}=0.10 \sim 0.15\) を設定する必要があることもわかっており,Smagorinsky定数はどんな流れ場でも共通して使える普遍定数ではないことがわかる
Smagorinskyモデルのメリットとデメリットは以下の通り
- SGS渦粘性係数が常に正 \(\nu_{_{SGS}}>0\) であり,数値計算の安定性が高い
- 適当なSmagorinsky定数を設定すれば,エネルギー散逸の総量に対してよいモデルになる
- Smagorinsky定数は普遍定数ではなく,流れ場に応じて適切に設定する必要がある
- SGS渦粘性係数が常に正 \(\nu_{_{SGS}}>0\) なので,SGSからGSへエネルギーが戻る逆カスケードを表現することができない
- 壁面で滑りなし条件 \(\left.\nu_{_{SGS}}\right|_{wall}=0\) を適用するために減衰関数\(f_{s}\)を必要とする
- GS成分に速度勾配があれば必ず \(\nu_{_{SGS}}>0\) となってしまうため,速度勾配はあるが乱流ではない領域がある流れ(層流から乱流への遷移,再層流化がある流れ)に対してはSmagorinskyモデルの使用/不使用を切り替えなければいけない
有名なモデルゆえデメリットが多く列挙されているが,2つのメリット(解くに数値安定性)が大きいので,幅広く利用されているモデルである
Smagorinskyモデルの導出
SGS渦粘性係数
流れ場にフィルターをかけると,流れ全体の運動エネルギー \(\overline{k}=\frac{\overline{u_{i}u_{i}}}{2}\)(乱流エネルギーではない)はGS成分 \(k_{_{GS}}=\frac{\overline{u}_{i}\overline{u}_{i}}{2}\)とSGS成分 \(k_{_{SGS}}=\frac{\overline{u_{i}u_{i}}-\overline{u}_{i}\overline{u}_{i}}{2}\) に分けられる
運動エネルギーのそれぞれの成分の輸送方程式は次のように表される
\begin{align}
&\frac{\partial k_{_{GS}}}{\partial t}
+\overline{u}_{j}\frac{\partial k_{_{GS}}}{\partial x_{j}}
=
\tau_{ij}\overline{S}_{ij}-\varepsilon_{_{GS}}
+\frac{\partial}{\partial x_{j}}
\left(-\overline{u}_{i}\tau_{ij}-\frac{\overline{p}\overline{u}_{j}}{\rho}+\nu\frac{\partial k_{_{GS}}}{\partial x_{j}}\right) \\
\\
&\frac{\partial k_{_{SGS}}}{\partial t}
+\overline{u}_{j}\frac{\partial k_{_{SGS}}}{\partial x_{j}}
=
-\tau_{ij}\overline{S}_{ij}-\varepsilon_{_{SGS}} \\
&\qquad +\frac{\partial}{\partial x_{j}}
\left\{\overline{u}_{i}\tau_{ij}-\frac{\overline{u_{i}u_{i}u_{j}}+\overline{u}_{j}\overline{u_{i}u_{i}}}{2}-\frac{\overline{pu_{j}}-\overline{p}\overline{u}_{j}}{\rho}+\nu\frac{\partial k_{_{SGS}}}{\partial x_{j}}\right\}
\end{align}
GS成分の輸送方程式においては\(\tau_{ij}S_{ij}\)の項がSGS運動エネルギーへの輸送率を表し,これを受けてSGS成分の輸送方程式では\(-\tau_{ij}S_{ij}\)の項がSGS運動エネルギーの生成率になる
SGSにおいて運動エネルギーの生成と散逸がつりあっているという局所平衡(GSからSGSに入ってきたエネルギーがすべてSGSにおいて熱として散逸していること)を仮定すると,SGSにおける運動エネルギーの散逸率\(\varepsilon_{_{SGS}}\)は次のようになる
\begin{equation}
\varepsilon_{_{SGS}}=-\tau_{ij} \overline{S}_{ij}
\tag{i}
\end{equation}
ここで突然SGS応力の渦粘性近似を行う
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}
\tag{ii}
\end{equation}
(i)に(ii)を代入すると次のようになる
\begin{align}
\varepsilon_{_{SGS}}
=-\left(\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}\right) \overline{S}_{ij}
=2\nu_{_{SGS}}\overline{S}_{ij}\overline{S}_{ij}-\frac{2}{3}k\delta_{ij}\overline{S}_{ij}
=2\nu_{_{SGS}}\overline{S}_{ij}\overline{S}_{ij}
\end{align}
ただし,\(\delta_{ij}\overline{S}_{ij}=\overline{S}_{kk}=0\)
Smagorinkyモデルを導出するために,\(\nu_{_{SGS}}\)と\(\varepsilon_{_{SGS}}\)を次元解析によって計算する
SGS渦粘性係数\(\nu_{_{SGS}}\)は速度\(q\)と長さ\(l\)の次元 \(\mathrm{[m^2/s]}\) を持つので,次元解析的に次のように表すことができる
\begin{equation}
\nu_{_{SGS}}=C_{\nu}ql
\tag{iii}
\end{equation}
同様に,エネルギー散逸率の次元 \(\mathrm{[m^2/s^3]}\) を考慮すると,\(\varepsilon_{_{SGS}}\)は次元解析的に次のように表せる
\begin{equation}
\varepsilon_{_{SGS}}=2\nu_{_{SGS}}\overline{S}_{ij}\overline{S}_{ij}=C_{\varepsilon}\frac{q^{3}}{l}
\tag{iv}
\end{equation}
(iii)と(iv)より,速度\(q\)について整理すると
\begin{equation}
\left\{\begin{array}{rcl}
q&=&\nu_{_{SGS}}/C_{\nu}l \\
q&=&\left(\frac{1}{C_{\varepsilon}}2\nu_{_{SGS}}l \overline{S}_{ij}\overline{S}_{ij}\right)^{\frac{1}{3}}
\end{array}\right.
\end{equation}
\begin{align}
\frac{\nu_{_{SGS}}}{C_{\nu}l}=\left(\frac{1}{C_{\varepsilon}}2\nu_{_{SGS}}l \overline{S}_{ij}\overline{S}_{ij}\right)^{\frac{1}{3}}
\rightarrow \quad
\nu_{_{SGS}}=\left\{\left(\frac{C_{\nu}^{3}}{C_{\varepsilon}}\right)^{\frac{1}{4}}l\right\}^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\end{align}
上式に長さのスケール\(l\)としてフィルター幅\(\Delta\)を用いて,定数をまとめると,Smagorinskyモデルの\(\nu_{_{SGS}}\)を求めることができる
\begin{equation}
\nu_{_{SGS}}=\left(C_{s}\Delta\right)^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\tag{v}
\end{equation}
SmagorinskyモデルのSGS渦粘性係数は
- SGSにおける運動エネルギーの生成と散逸における局所平衡
- 渦粘性係数とエネルギー散逸率の次元解析
によって導出されている
Smagorinsky定数
(v)を(iv)に代入すると,次のようになる
\begin{align}
&\varepsilon_{_{SGS}}=2\left\{\left(C_{s}\Delta\right)^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}\right\}\overline{S}_{ij}\overline{S}_{ij}
=\left(C_{s}\Delta\right)^{2}\left(2\overline{S}_{ij}\overline{S}_{ij}\right)^{\frac{3}{2}} \\
\\ &\rightarrow\quad
|\mathbf{S}|^{2}=\overline{S}_{ij}\overline{S}_{ij}=\frac{\varepsilon_{_{SGS}}^{2/3}}{2\left(C_{s}\Delta\right)^{4/3}}
\tag{vi}
\end{align}
ここで,フィルター幅\(\Delta\)が慣性小領域にあるように格子分割を定めると,その波数\(k\)付近のエネルギースペクトル\(E(k)\)は-5/3乗則 \(E(k)=\alpha\varepsilon^{\frac{2}{3}}k^{-\frac{5}{3}}\) に従うと考えられる(\(k\)は波数で\(\varepsilon\)は粘性散逸総量)
このとき,\(|\mathbf{S}|^{2}=\overline{S}_{ij}\overline{S}_{ij}\) は渦度スペクトル関数の波数積分から次のように求められる
\begin{align}
|\mathbf{S}|^{2}=\int_{0}^{\pi/4} k^{2}E(k)\:dk
=\frac{3}{4}\alpha|\varepsilon|^{\frac{2}{3}}\left(\frac{\pi}{\Delta}\right)^{\frac{4}{3}}
\tag{vii}
\end{align}
SGSスケールの運動エネルギー散逸率とエネルギースペクトルにおける粘性散逸総量が等しい \(\varepsilon_{_{SGS}}=\varepsilon\) とすると,(vi)と(vii)よりSmagorinsky定数が計算できる
\begin{align}
\frac{\varepsilon_{_{SGS}}^{2/3}}{2\left(C_{s}\Delta\right)^{4/3}}
=\frac{3}{4}\alpha|\varepsilon_{_{SGS}}|^{\frac{2}{3}}\left(\frac{\pi}{\Delta}\right)^{\frac{4}{3}}
\quad \rightarrow \quad
C_{s}=\frac{1}{\pi}\left(\frac{2}{3\alpha}\right)^{\frac{3}{4}}
\end{align}
ここで,実験的に \(\alpha=1.5\) であることが確認されているので,Smagorinsky定数の理論値 \(C_{s}=0.173\) が導かれる
Smagorinsky定数の理論値は,
- SGSにおける運動エネルギーの生成と散逸における局所平衡
- フィルター幅\(\Delta\)が慣性小領域にあるとしたときのエネルギースペクトルの-5/3乗則
- SGSエネルギー散逸率と粘性散逸総量が等しいという仮定
によって導出されている
Dynamic Smagorinskyモデル
Dynamic Smagorinskyモデルでは,Smagorinskyモデルの定数\(C_{s}\)を変数と考え,GSの流れ場の情報から動的に\(C_{s}\)を決定する
そのために,グリッドフィルター\(\overline{G}\)(LESの基礎方程式を求めるときに使ったフィルター)とテストフィルター\(\tilde{G}\)(GSの流れ場に対してかけられるフィルター)の2種類のフィルター操作を考える
2つのフィルターは違う種類のフィルターで,グリッドフィルターのフィルター幅\(\overline{\Delta}\)よりもテストフィルターのフィルター幅\(\tilde{\Delta}\)が大きくなるように設定する
\begin{equation}
\gamma=\tilde{\Delta}/\overline{\Delta}>1
\end{equation}
上記2種類のフィルター操作によって,Dynamic Smagorinskyモデルにおける渦粘性係数\(\nu_{_{SGS}}\)と\(C\)は次の式で与えられる
\begin{equation}
\nu_{_{SGS}}=C\Delta^{2}|\overline{S}|, \qquad
C=-\frac{1}{2\overline{\Delta}^{2}}\frac{\left[L_{ij}M_{ij}\right]}{\left[M_{kl}M_{kl}\right]}
\end{equation}
\begin{equation}
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}, \qquad
M_{ij}=\gamma |\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\widetilde{|\overline{S}|\overline{S}_{ij}}
\end{equation}
ここで,\(\overline{S}_{ij}\)はひずみ速度テンソルであり,\(|\overline{S}|\)は次の式で定義されている
\begin{equation}
|\overline{S}|=\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\end{equation}
\([\quad]\)は数値計算を安定化させるために用いられる何らかの平均操作(一様乱流では体積平均,平行平板間乱流では面平均,矩形ダクト内乱流では軸方向線上での平均,など)や上限下限の制限を表す
Dynamic Smagorinskyモデルのメリットとデメリットは以下の通り
- フィルター幅の比さえ決めれば,経験的な定数を一切使わずに渦粘性係数を求められる
- グリッドフィルターとテストフィルターの両スケールの間に乱れがなければ \(L_{ij}=0\)となり,渦粘性も\(0\)になることから,層流・乱流遷移の切り替えや壁面近傍の減衰関数が必要ない
- \(C\)の値は \(C<0\) にもなりうるので,エネルギーの逆カスケードを表現することができる
- \(C\)の値は空間的に大きく変動し,数値的に不安定である
- 実際の計算では\(C\)の変動を緩和するために何らかの平均操作を行う必要があり,Dynamicモデルの概念から大幅に後退せざるを得ない
Dynamic Smagorinskyモデルの導出
エネルギーカスケードの考え方より,SGSの流れの挙動は,GSの流れの中でもより小さく,SGSに近いスケールの流れによって決定されていると考えられる
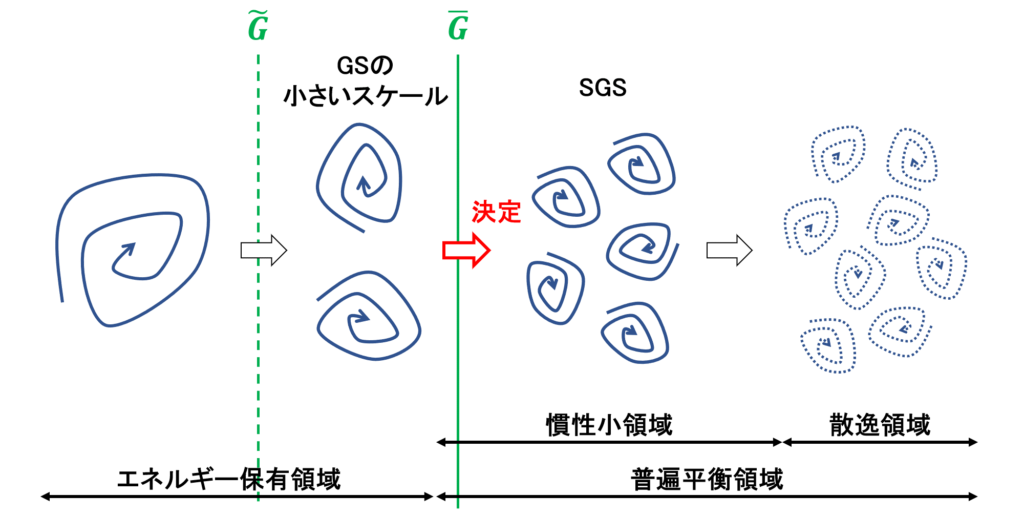
そこで,GSの中からより小さいスケールを取り出すため,Filtered Naver-Stokes方程式にさらにフィルターをかけることを考える
\begin{align}
\frac{\partial \widetilde{\overline{u}}_{i}}{\partial t}
+\frac{\partial \widetilde{\overline{u_{i}u_{j}}}}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \widetilde{\overline{p}}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{2\nu\widetilde{\overline{S}}_{ij}\right\}
\end{align}
両辺から\(\frac{\partial \widetilde{\overline{u_{i}u_{j}}}}{\partial x_{j}}\)を引いて\(\frac{\partial \widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}}{\partial x_{j}}\)を足すと
\begin{align}
\frac{\partial \widetilde{\overline{u}}_{i}}{\partial t}
+\frac{\partial \widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \widetilde{\overline{p}}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{2\nu\widetilde{\overline{S}}_{ij}-T_{ij}\right\}
\end{align}
サブテストフィルタースケール応力\(T_{ij}\)(GSの中の小さいスケールの乱れ)
\begin{equation}
T_{ij}=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}_{i}\overline{u}_{j}}
\end{equation}
が求まる
サブテストフィルタースケール応力がSGSの乱れに与える影響を考えるために,\(T_{ij}\)と\(\tau_{ij}\)の関係式を求める
\(\tau_{ij}\)にテストフィルターをかけると
\begin{align}
\widetilde{\tau}_{ij}=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}_{i}\overline{u}_{j}}
=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}
-\left(\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}\right)
=T_{ij}-L_{ij}
\end{align}
\(T_{ij}\)と\(\tau_{ij}\)の関係式
\begin{equation}
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}=T_{ij}-\widetilde{\tau}_{ij}
\tag{i}
\end{equation}
を求めることができる
\(L_{ij}\)は,サブテストフィルタースケール応力に対するレナード項にあたり,既知の速度成分\(\overline{u}_{i}\)のみで構成されているので直接計算で求めることができる(\(\overline{u_{i}u_{j}}\)は二次の相関項なので計算できない)
\(T_{ij}\)と\(\tau_{ij}\)の関係式からSmagorinsky定数を計算するために,それぞれのスケールの乱流応力にSmagorinskyモデルを適用する
\begin{align}
T_{ij}-\frac{1}{3}T_{kk}\delta_{ij}
&=-2C\tilde{\Delta}^{2}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij} \\
\tilde{\tau}_{ij}-\frac{1}{3}\tilde{\tau}_{kk}\delta_{ij}
&=-2C\overline{\Delta}^{2}\widetilde{|\overline{S}|\overline{S}_{ij}}
\tag{ii}
\end{align}
\(\tilde{\Delta}\)はテストフィルターのフィルター幅,\(\overline{\Delta}\)はグリッドフィルターのフィルター幅である
(ii)を(i)に代入すると次のようになる
\begin{equation}
L_{ij}-\frac{1}{3}\left(T_{kk}-\tilde{\tau}_{kk}\right)\delta_{ij}
=T_{ij}-\frac{1}{3}T_{kk}\delta_{ij}-\left(\widetilde{\tau}_{ij}-\frac{1}{3}\widetilde{\tau}_{kk}\delta_{ij}\right) \\
\end{equation}
\begin{equation}
\rightarrow \quad
L_{ij}^{a}
=-2C\tilde{\Delta}^{2}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\left(-2C\overline{\Delta}^{2}\widetilde{|\overline{S}|\overline{S}_{ij}}\right)
=-2C\overline{\Delta}^{2}\left(\frac{\tilde{\Delta}^{2}}{\overline{\Delta}^{2}}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\widetilde{|\overline{S}|\overline{S}_{ij}}\right)
\end{equation}
\(L_{ij}^{a}=L_{ij}-\frac{1}{3}L_{kk}\delta_{ij}\) は \(L_{ij}\) の非等方テンソル(anisotropic tensor)であり,テストフィルターとグリッドフィルターのフィルター幅の比を \(\gamma=\tilde{\Delta}/{\overline{\Delta}}\)とすれば次のようになる
\begin{equation}
L_{ij}^{a}=-2C\overline{\Delta}^{2}M_{ij}
\tag{iii}
\end{equation}
\begin{equation}
M_{ij}=\gamma^{2}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\widetilde{|\overline{S}|\overline{S}_{ij}}
\end{equation}
ここで,\(L_{ij}^{a}\) と \(-2C\overline{\Delta}^{2}M_{ij}\) は対称テンソルかつトレースレス \(L_{kk}=-2C\overline{\Delta}^{2}M_{kk}=0\) なので,それぞれの独立な成分は5つである
1つのスカラー\(C\)だけを用いて2つのテンソルの独立な5つの成分をすべて一致させることはできないので,2つのテンソルの誤差が最小になるように,最小二乗法を用いて\(C\)を決定する
(iii)の両辺を比較したときの誤差テンソルを \(e_{ij}=L_{ij}^{a}-\left(-2\overline{\Delta}^{2}M_{ij}\right)\) としたとき,最小二乗法より\(e_{ij}\)の二乗を考えると
\begin{align}
&E=e_{ij}e_{ij}=\left(L_{ij}^{a}+2C\overline{\Delta}^{2}M_{ij}\right)^{2}\\
\\
\rightarrow \quad
&\frac{\partial E}{\partial C}
=2\left(L_{ij}^{a}+2C\overline{\Delta}^{2}M_{ij}\right)2\overline{\Delta}^{2}M_{ij}
=4\overline{\Delta}^{2}\left(L_{ij}^{a}M_{ij}+2C\overline{\Delta}^{2}M_{ij}M_{ij}\right)
\end{align}
となり,誤差を最小にするには \(\frac{\partial E}{\partial C}=0\) となればいいので
\begin{align}
&\frac{\partial E}{\partial C}
=4\overline{\Delta}^{2}\left(L_{ij}^{a}M_{ij}+2C\overline{\Delta}^{2}M_{ij}M_{ij}\right)=0 \\
\\ \rightarrow \quad
&L_{ij}^{a}M_{ij}+2C\overline{\Delta}^{2}M_{ij}M_{ij}=0
\end{align}
よって,Dynamic Smagorinskyモデルの係数\(C\)は次のようになる
\begin{equation}
C=-\frac{1}{2\overline{\Delta}^{2}}\frac{L_{ij}^{a}M_{ij}}{M_{ij}M_{ij}}
\end{equation}
実際の計算では\(C\)の値の変動を緩和するため,右辺の分母分子にそれぞれ何らかの平均値を用いる必要がある
\begin{equation}
C=-\frac{1}{2\overline{\Delta}^{2}}\frac{\left[L_{ij}^{a}M_{ij}\right]}{\left[M_{ij}M_{ij}\right]}
\end{equation}
まとめ
Smagorinskyモデルの導出とDynamicモデルの解説を行った
Smagorinskyモデルは,フィルター幅\(\Delta\)とひずみ速度テンソル\(S_{ij}\)によってSGS渦粘性係数を計算する0方程式モデルである
数値的に安定であり,適切な定数\(C_{s}\)を与えればエネルギー散逸に対して精度の高いモデルになることから,幅広く利用されている
Dynamic Smagorinskyモデルを使えば,係数\(C\)を動的に計算することができる
↓おすすめ記事
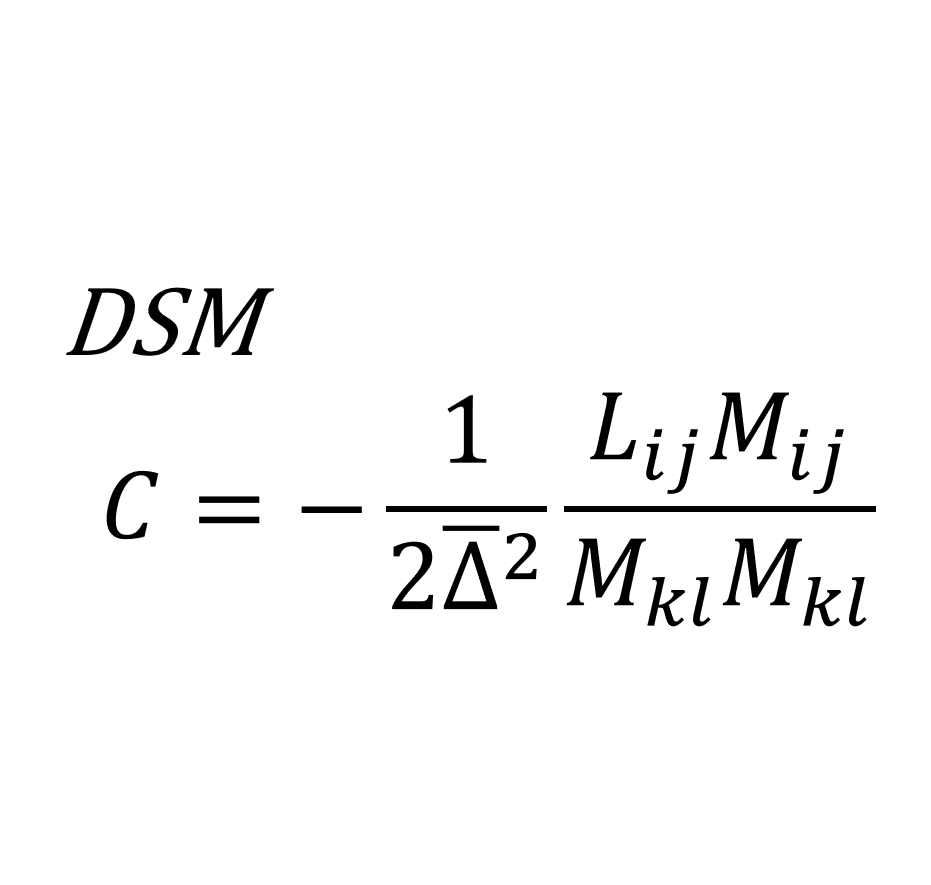


コメント