SGS応力のモデル化の基礎となっているエネルギーカスケードという考え方について説明する
keyword: エネルギーカスケード，エネルギー保有領域，普遍平衡領域，慣性小領域，散逸領域
エネルギーカスケード
流れ場に存在する乱れ（渦）の生成と消滅の過程は次のようになる
- 流れ場のスケール（壁面の段差や航空機の翼）からエネルギーが与えられて大きな渦が生成される
- 大きな渦が分裂を繰り返して小さな渦になる
- 最終的にこれ以上分裂できない最小スケールになった渦が粘性によって熱となって散逸する
このような，外部から大きい渦へ注入されたエネルギーが小さな渦へと段階的に伝達していく過程のことを エネルギーカスケード（Energy cascade）という
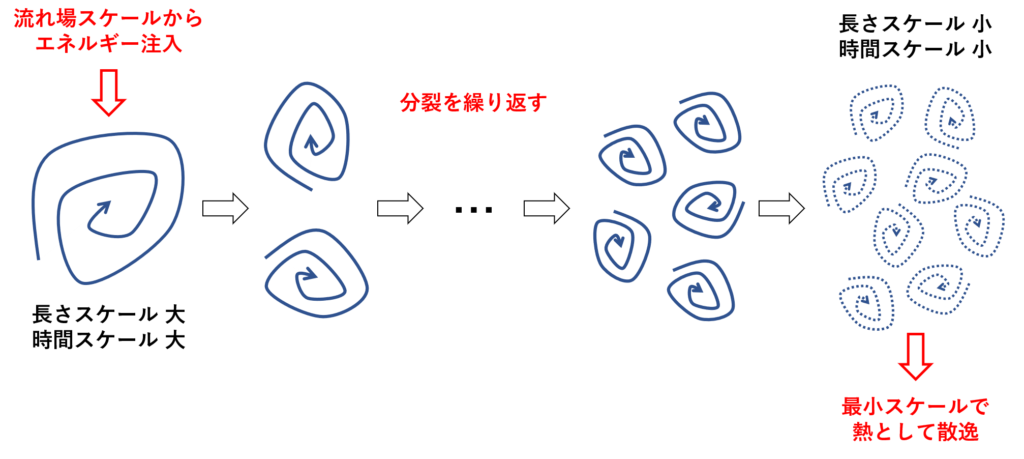
最初に作られた大きな渦は流れ場の影響を受けており，統計的な非等方性が現れる（大きな渦の形状や数は流れ場に依存する）が，渦が分裂するにしたがって最初の渦が持っていた非等方性はなくなっていき，何度も分裂を繰り返したある程度の小さいスケールの渦は流れ場に依存しない等方的な渦になると考えられる
このような考え方を局所等方性（局所＝小さいスケールでの）といい，流れ場の影響を受けない小さいスケールの渦はどんな流れ場に対しても普遍的なものであるという仮定を「コルモゴロフの第一相似則」という
局所等方性をもつような小さいスケールの渦は，流れ場によって作られる大きな渦と比べて時間スケール（分裂や合体にかかる時間）が非常に小さく，常に平衡状態にあるとみなせる
よって，局所等方性が成り立ち平衡状態にある普遍的な渦のスケールを「普遍平衡領域」とよぶ
また，流れ場に存在する乱れのエネルギーに注目すると，普遍平衡領域の渦のもつエネルギーはほとんどなく，その大部分は流れ場の形状に依存する大きな渦が担っている
普遍平衡領域に対して，流れ場の形状に依存し，乱れエネルギーの大部分を保有する大きな渦のスケールを「エネルギー保有領域」とよぶ
LESは，普遍平衡領域の乱れをモデル化し，エネルギー保有領域の乱れを直接格子上で計算することで，どんな流れ場にも使える普遍的なモデルとなっている
渦（乱れ）が流れ場のスケールによって生成され，分裂を繰り返し，これ以上分裂できない最小スケールにおいて粘性によって熱として散逸する過程をエネルギーカスケードという
何度も分裂を繰り返した小さなスケールの渦は，流れ場の形状に依存せず，どんな流れ場においても普遍的なものになる（コルモゴロフの第一相似則）
乱れのスケールは，乱れエネルギーの大部分を担っている大きなスケールである「エネルギー保有領域」と，局所等方性をもち平衡状態にある小さなスケールである「普遍平衡領域」に分けられる
LESでは普遍平衡領域の乱れをモデル化する
慣性小領域
渦が粘性によって熱として散逸していく渦のスケールを「散逸領域」といい，普遍平衡領域の中でも最も小さいスケールである
前々回の記事で説明したように，流れ場の代表スケール（エネルギー保有領域のスケール）\(l\)と流れ場に存在する渦の最小スケール（散逸領域のスケール）\(\eta\)には次のような関係がある
\begin{equation}
\frac{l}{\eta}={Re}^{\frac{3}{4}}
\end{equation}
この式は，レイノルズ数が大きくなるとその3/4乗に比例してエネルギー保有領域と散逸領域のスケールが離れていくことを意味している
レイノルズ数が十分に高い流れ場では，エネルギー保有領域と散逸領域には大きな隔たりがあり，大きな渦が分裂を繰り返して普遍平衡領域に入ってからしばらくはひたすら分裂を続けるだけの領域がある
このように，普遍平衡領域の中で粘性による散逸の影響を受けずに分裂だけを繰り返す領域を「慣性小領域」とよぶ
また，このような領域が存在するという仮説を「コルモゴロフの第二相似則」という
レイノルズ数が十分に高い流れ場では，普遍平衡領域は慣性小領域と散逸領域に分けらえる
渦は，慣性小領域ではエネルギーを保持したまま分裂を繰り返し，散逸領域にて粘性によって熱に変換される
エネルギースペクトル
これまでの説明をグラフにしたものがエネルギースペクトルである
グラフの縦軸に乱れの速度をフーリエ変換して得られるエネルギースペクトル\(E(k)\)をとり，横軸に乱れの波数\(k\)をとると，次のようになる
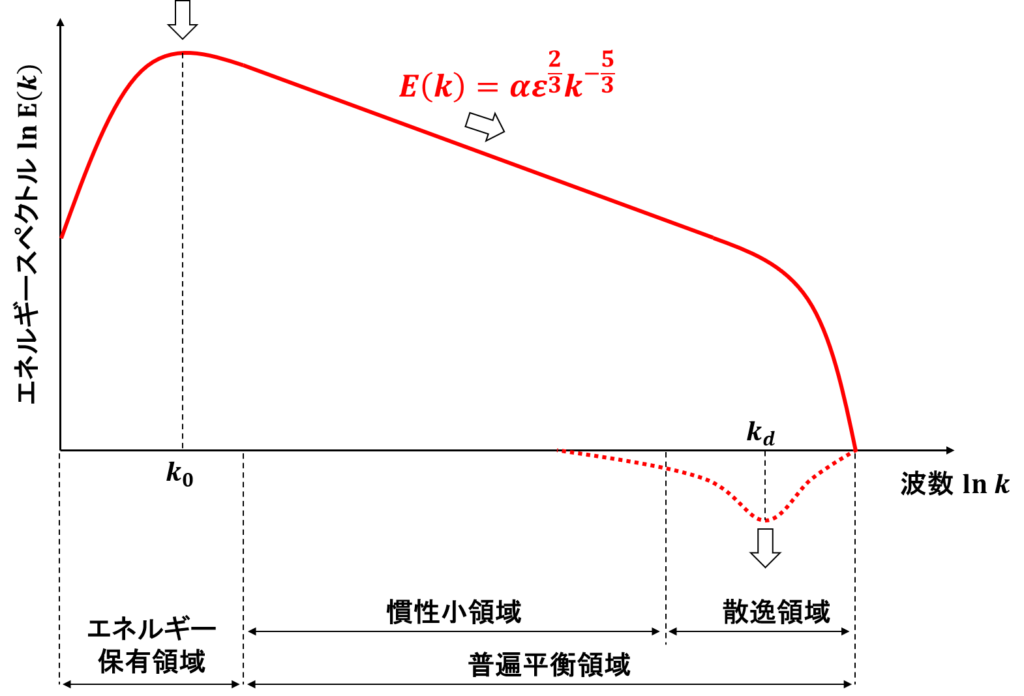
グラフ左側の波数が小さい（波長が大きい）領域がエネルギー保有領域であり，流れ場からエネルギーをもらうとともに流れ場の大部分のエネルギーを保有している
グラフ右側の波数が大きい（波長が小さい）領域が散逸領域であり，粘性による散逸によってエネルギースペクトルが急速に減少している
グラフ中央の領域が慣性小領域であり，慣性小領域におけるエネルギースペクトルは次元解析によって次のように求められる
\begin{equation}
E(k)=\alpha \varepsilon^{2}{3}k^{-\frac{5}{3}}
\end{equation}
慣性小領域における-5/3乗スペクトルは実験でも確認されており，係数\(\alpha\)は実験的に \(\alpha=1.2 \sim 2.0\)であることがわかっている
LESのモデルにおいては，格子サイズを慣性小領域に設定することを前提としており，慣性小領域を境にGS成分とSGS成分が隔てられている
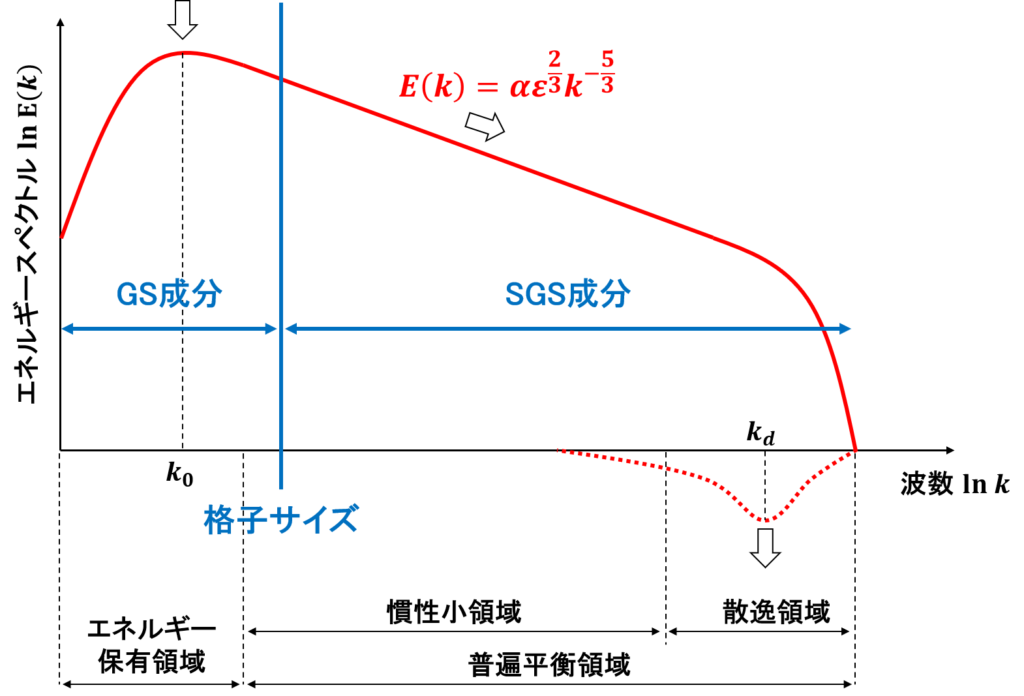
LESでは格子サイズを慣性小領域に設定する
慣性小領域ではエネルギースペクトルについて-3/5乗則がなりたつ
\begin{equation}
E(k)=\alpha \varepsilon^{2}{3}k^{-\frac{5}{3}}
\end{equation}
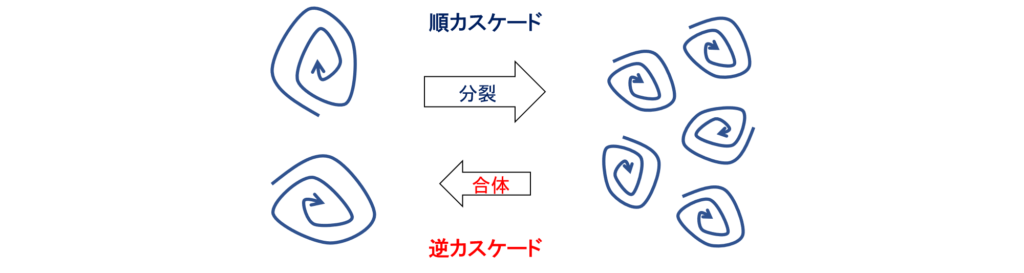
順カスケードと逆カスケード
乱れのエネルギーが渦の分裂によってより小さい渦へと伝達していく過程を「順カスケード」といい，その逆に，小さい渦が合体することによって乱れのエネルギーが大きな渦へと伝達していく過程を「逆カスケード」という
乱れの中では常に順カスケードと逆カスケードが起こっているが，それらは相対的に非常に小さな時間スケールで起こっており平衡状態にある
全体としては順カスケードのほうが多いため，平均的に見ると，渦はより小さい渦へと分裂していく順カスケードにあるとみなせる
まとめ
SGS応力のモデル化の基礎となっているエネルギーカスケードという考え方について説明した
だいたい数値流体力学の教科書の最初のほうに書いてあって，よくわからないまま読み進めていくことになる概念だが，ここら辺を理解しておくとLESの説明がなんとなくわかるようになる
↓おすすめ記事
コメント