k Equationモデルの説明とDynamicモデルの導出を行う
keyword: k Equationモデル,Dynamicモデル
Filtered Navier-Stokes方程式
LESの基礎方程式はフィルターを施した連続の式とNavier-Stokes方程式である
フィルターをかけた基礎方程式は次のように表される
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{_{SGS}}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
上式において,SGSの乱れの効果を表すSGS応力は渦粘性近似によって次のようにモデル化されている
\begin{equation}
\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}
=\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}
\end{equation}
\(\nu_{_{SGS}}\)はSGS渦粘性係数であり,\(\overline{S}_{ij}\)はひずみ速度テンソル \(\overline{S}_{ij}=\frac{1}{2}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\) である
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数はSGS渦粘性係数\(\nu_{_{SGS}}\)ただ1つであり,この\(\nu_{_{SGS}}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
k Equationモデル
k Equationモデルは乱流エネルギー\(k\)を用いた1方程式モデルである
k Equationモデルでは,SGS渦粘性係数\(\nu_{_{SGS}}\)は次の式で定義される
\begin{equation}
\nu_{_{SGS}}=C_{k}\Delta\sqrt{k_{_{SGS}}}
\end{equation}
\(C_{k}\)はモデル定数,\(k_{_{SGS}}\)はSGS乱流エネルギーであり,\(k_{_{SGS}}\)は以下の輸送方程式を解くことによって求められる
\begin{equation}
\frac{\partial k_{_{SGS}}}{\partial t}
+\overline{u}_{j}\frac{\partial k_{_{SGS}}}{\partial x_{j}}
=
-\tau_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}-\varepsilon_{_{SGS}}
+\frac{\partial}{\partial x_{j}}\left\{\left(\nu+\nu_{_{SGS}}\right)\frac{\partial k_{_{SGS}}}{\partial x_{j}}\right\}
\end{equation}
ここで,\(\varepsilon_{_{SGS}}\)は次元解析によって次のように計算される
\begin{equation}
\varepsilon_{_{SGS}}=C_{\varepsilon}\frac{k_{_{SGS}}^{\frac{3}{2}}}{\Delta}
\end{equation}
OpenFOAMに実装されているk Equationモデルでは,モデル定数として \(C_{k}=0.094\),\(C_{\varepsilon}=1.048\)が使われている
≫OpenFOAM User Guide k Equation
≫Yoshizawa, A., Horiuti, K. A Statistically-Derived Subgrid-Scale Kinetic Energy Model for the Large-Eddy Simulation of Turbulent Flows (1985) Journal of the Physical Society of Japan, 54 (8), pp. 2834-2839.
Dynamic k Equationモデル
k Equationモデルでは,GSの流れ場から定数を動的に計算するDynamicモデルが提案されている
そのために,グリッドフィルター\(\overline{G}\)(LESの基礎方程式を求めるときに使ったフィルター)とテストフィルター\(\tilde{G}\)(GSの流れ場に対してかけられるフィルター)の2種類のフィルター操作を考える
2つのフィルターは違う種類のフィルターで,グリッドフィルターのフィルター幅\(\overline{\Delta}\)よりもテストフィルターのフィルター幅\(\tilde{\Delta}\)が大きくなるように設定する
\begin{equation}
\gamma=\tilde{\Delta}/\overline{\Delta}>1
\end{equation}
上記2種類のフィルター操作によって,Dynamic k Equationモデルでは,\(C_{k}\)および\(C_{\varepsilon}\)は次のように与えられる
\begin{equation}
C_{k}=-\frac{1}{2}\frac{L_{ij}^{a}M_{ij}}{M_{kl}M_{kl}}, \qquad
C_{\varepsilon}=\frac{\left(\nu+\nu_{_{SGS}}\right)\widetilde{\Delta}}{k_{_{test}}^{3/2}}
\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right)
\end{equation}
\begin{equation}
L_{ij}^{a}=L_{ij}-\frac{1}{3}L_{kk}\delta_{ij}, \qquad
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}, \qquad
M_{ij}=-\widetilde{\Delta}\sqrt{k_{_{test}}}\widetilde{\overline{S}}_{ij}, \qquad
k_{_{test}}=\frac{L_{ii}}{2}
\end{equation}
導出
エネルギーカスケードの考え方より,SGSの流れの挙動は,GSの流れの中でもより小さく,SGSに近いスケールの流れによって決定されていると考えられる
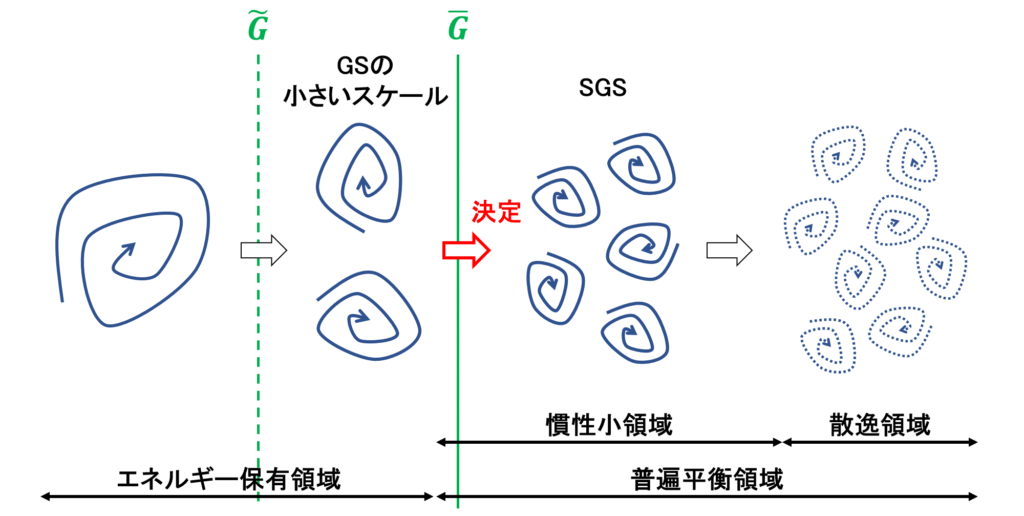
そこで,GSの中からより小さいスケールを取り出すため,Filtered Naver-Stokes方程式にさらにフィルターをかけることを考える
\begin{align}
\frac{\partial \widetilde{\overline{u}}_{i}}{\partial t}
+\frac{\partial \widetilde{\overline{u_{i}u_{j}}}}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \widetilde{\overline{p}}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{2\nu\widetilde{\overline{S}}_{ij}\right\}
\end{align}
両辺から\(\frac{\partial \widetilde{\overline{u_{i}u_{j}}}}{\partial x_{j}}\)を引いて\(\frac{\partial \widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}}{\partial x_{j}}\)を足すと
\begin{align}
\frac{\partial \widetilde{\overline{u}}_{i}}{\partial t}
+\frac{\partial \widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \widetilde{\overline{p}}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{2\nu\widetilde{\overline{S}}_{ij}-T_{ij}\right\}
\end{align}
サブテストフィルタースケール応力\(T_{ij}\)(GSの中の小さいスケールの乱れ)
\begin{equation}
T_{ij}=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}_{i}\overline{u}_{j}}
\end{equation}
が求まる
サブテストフィルタースケール応力がSGSの乱れに与える影響を考えるために,\(T_{ij}\)と\(\tau_{ij}\)の関係式を求める
\(\tau_{ij}\)にテストフィルターをかけると
\begin{align}
\widetilde{\tau}_{ij}=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}_{i}\overline{u}_{j}}
=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}
-\left(\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}\right)
=T_{ij}-L_{ij}
\end{align}
\(T_{ij}\)と\(\tau_{ij}\)の関係式
\begin{equation}
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}=T_{ij}-\widetilde{\tau}_{ij}
\tag{i}
\end{equation}
を求めることができる
\(L_{ij}\)は,サブテストフィルタースケール応力に対するレナード項にあたり,既知の速度成分\(\overline{u}_{i}\)のみで構成されているので直接計算で求めることができる(\(\overline{u_{i}u_{j}}\)は二次の相関項なので計算できない)
ここで,テストフィルターをかけた流れ場における流体の運動エネルギー\(\widetilde{k}\)とエネルギー散逸率\(\widetilde{\varepsilon}\)を考えると,次のようにテストフィルタースケールとサブテストフィルタースケールに分けることができる
\begin{align}
&\widetilde{k}=\frac{1}{2}\widetilde{\overline{u}_{i}\overline{u}_{i}}
=\frac{1}{2}\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{i}
+\frac{1}{2}\left(\widetilde{\overline{u}_{i}\overline{u}_{i}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{i}\right)
\\ \\
&\widetilde{\varepsilon}=\left(\nu+\nu_{_{SGS}}\right)\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
=\left(\nu+\nu_{_{SGS}}\right)\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}+\left(\nu+\nu_{_{SGS}}\right)\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right)
\end{align}
上式の中で,サブテストフィルタースケール(GSの中の小さいスケール)の運動エネルギー\(k_{_{test}}\)とエネルギー散逸率\(\varepsilon_{_{test}}\)は次の部分である
\begin{align}
&k_{_{test}}=\frac{1}{2}\left(\widetilde{\overline{u}_{i}\overline{u}_{i}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{i}\right)=\frac{L_{ii}}{2}
\\ \\
&\varepsilon_{_{test}}=
\left(\nu+\nu_{_{SGS}}\right)\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right)
\tag{i}
\end{align}
サブテストフィルタースケールは壁面から離れた十分にレイノルズ数の高い領域なので,エネルギーの散逸は分子粘性と渦粘性の両方によって担われている(\(\nu+\nu_{_{SGS}}\))
\(C_{k}\)
サブテストフィルタースケール応力のレナード項\(L_{ij}\)とSGS応力\(\tau_{ij}\)は相似の関係にあることがわかっている
そこで,\(L_{ij}\)に対してk Equationモデルを適用する
\begin{align}
&L_{ij}-\frac{1}{3}L_{kk}\delta_{ij}
=-2C_{k}\widetilde{\Delta}\sqrt{k_{_{test}}}\widetilde{\overline{S}}_{ij} \\
\rightarrow \quad
&L_{ij}^{a}=-2C_{k}M_{ij}, \qquad
M_{ij}=\widetilde{\Delta}\sqrt{k_{_{test}}}\widetilde{\overline{S}}_{ij}
\end{align}
この式に対して,Dynamic Smagorinskyモデルと同様に最小二乗法を用いると
\begin{equation}
e_{ij}=L_{ij}^{a}-\left(-2C_{k}M_{ij}\right), \quad
E=e_{ij}e_{ij}=\left(L_{ij}^{a}+2C_{k}M_{ij}\right)^{2}
\end{equation}
\begin{equation}
\frac{\partial E}{\partial C_{k}}
=2\left(L_{ij}^{a}+2C_{k}M_{ij}\right)2M_{ij}
=4\left(L_{ij}^{a}M_{ij}+2C_{k}M_{ij}M_{ij}\right)=0 \\
\end{equation}
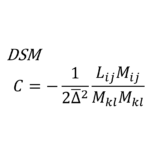
\(C_{k}\)は次のように導かれる
\begin{equation}
C_{k}=-\frac{1}{2}\frac{L_{ij}M_{ij}}{M_{kl}M_{kl}}
\end{equation}
\(C_{\varepsilon}\)
\(\varepsilon_{_{SGS}}\)と同様に,\(\varepsilon_{_{test}}\)は次の式で表される
\begin{equation}
\varepsilon_{_{test}}=C_{\varepsilon}\frac{k_{_{test}}^{\frac{3}{2}}}{\widetilde{\Delta}}
\tag{ii}
\end{equation}
(i)と(ii)より,\(C_{\varepsilon}\)を導くことができる
\begin{align}
C_{\varepsilon}\frac{k_{_{test}}^{\frac{3}{2}}}{\widetilde{\Delta}}
=
\left(\nu+\nu_{_{SGS}}\right)\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right) \\
\\ \rightarrow \quad
C_{\varepsilon}
=
\frac{\left(\nu+\nu_{_{SGS}}\right)\widetilde{\Delta}}{k_{_{test}}^{3/2}}\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right) \\
\end{align}
参考
≫OpenFOAM User Guide Dynamic k eqn
≫W-W Kim and S. Menon. A new dynamic one-equation subgrid-scale model for large eddy simulations. In 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 1995.
以下のサイトにあるPDFのpp.184-193が上記の論文
≫A New Approach to Validate Subgrid Models in Complex High Reynolds Number Flows.
まとめ
k Equationモデルの説明とDynamicモデルの導出を行った
k Equationモデルは,フィルター幅\(\Delta\)とSGS乱流エネルギー\(k_{_{SGS}}\)を用いてSGS渦粘性係数を与える1方程式モデルである
Dynamic k Equationモデルを使えば,2つの係数\(C_{k}\),\(C_{\varepsilon}\)を動的に計算することができる
↓おすすめ記事
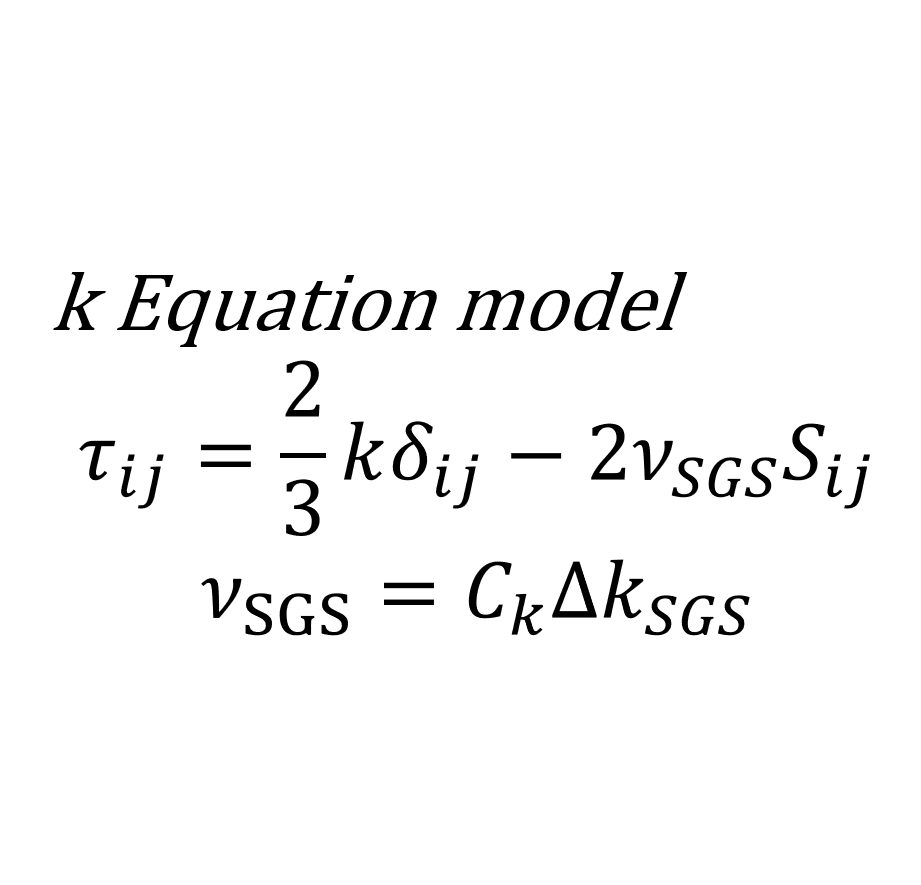


コメント