OpenVSPのPythonAPIで地面効果を計算する
はじめに
OpenVSPのPythonAPIで地面効果を計算する
OpenVSPはVLM（Vortex Lattice Method / 渦格子法）を用いた解析ソフトなので、地面効果を計算するために鏡像法を用いている
↓参考
最終的にはこんな感じになる
それでは行ってみよう
ソースコード
↓ソースコードはこれ
def vsp_sweep_wig(vsp, alpha, mach, reynolds, height, AnalysisMethod=0, verbose=1):
# wig : wing in ground effect
if verbose:
print('\n-> Calculate alpha & mach sweep analysis\n')
# //==== Analysis: VSPAero Compute Geometry to Create Vortex Lattice DegenGeom File ====//
# Set defaults
compgeom_name = 'VSPAEROComputeGeometry'
vsp.SetAnalysisInputDefaults(compgeom_name)
if AnalysisMethod:
vsp.SetIntAnalysisInput(compgeom_name, 'AnalysisMethod', [AnalysisMethod], 0)
# List inputs, type, and current values
if verbose:
print(compgeom_name)
vsp.PrintAnalysisInputs(compgeom_name)
print('')
# Execute
if verbose:
print('\tExecuting...')
compgeom_resid = vsp.ExecAnalysis(compgeom_name)
if verbose:
print('\tCOMPLETE')
# Get & Display Results
if verbose:
vsp.PrintResults(compgeom_resid)
print('')
# //==== Analysis: VSPAero Sweep ====//
# Set defaults
analysis_name = 'VSPAEROSweep'
vsp.SetAnalysisInputDefaults(analysis_name)
# Reference geometry set
geom_set = [0]
vsp.SetIntAnalysisInput(analysis_name, 'GeomSet', geom_set, 0)
ref_flag = [1]
vsp.SetIntAnalysisInput(analysis_name, 'RefFlag', ref_flag, 0)
wid = vsp.FindGeomsWithName('WingGeom')
vsp.SetStringAnalysisInput(analysis_name, 'WingID', wid, 0)
df = pd.DataFrame()
for re in reynolds:
for ma in mach:
for he in height:
for al in alpha:
# Freestream Parameters
vsp.SetDoubleAnalysisInput(analysis_name, "AlphaStart", [al], 0)
vsp.SetIntAnalysisInput(analysis_name, "AlphaNpts", [1], 0)
vsp.SetDoubleAnalysisInput(analysis_name, 'MachStart', [ma], 0)
vsp.SetIntAnalysisInput(analysis_name, 'MachNpts', [1], 0)
vsp.SetDoubleAnalysisInput(analysis_name, 'ReCref', [re], 0)
vsp.SetIntAnalysisInput(analysis_name, 'ReCrefNpts', [1], 0)
vsp.Update()
# Ground Effect
vsp.SetIntAnalysisInput(analysis_name, 'GroundEffectToggle', [1], 0)
vsp.SetDoubleAnalysisInput(analysis_name, 'GroundEffect', [he], 0)
# List inputs, type, and current values
if verbose:
print(analysis_name)
vsp.PrintAnalysisInputs(analysis_name)
print('')
# Execute
if verbose:
print('\tExecuting...')
rid = vsp.ExecAnalysis(analysis_name)
print('\tCOMPLETE')
else:
with suppress_stdout():
rid = vsp.ExecAnalysis('VSPAEROSweep')
tmp = get_polar_result(rid)
bref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'bref')[0] # [m]
tmp['Alpha'], tmp['Height'], tmp['H_bref'] = al, he, he/bref
df = pd.concat([df, tmp])
return df地面効果を含めたスイープ計算をする関数
引数
vsp：OpenVSPのオブジェクト
alpha：迎角(deg) [list of float]
mach：マッハ数 [list of float]
reynolds：Re数 [list of float]
height：高度(m) [list of float]
AnalysisMethod=0：解析手法 (0: VLM, 1: Panel Method) [int]
返値
df：解析結果のデータフレーム [pd.DataFrame]
↓使い方の例はこれ
import sys
import os
import numpy as np
import pandas as pd
# ../bin/AnalysisVSPAERO.py をモジュールとしてインポート
sys.path.append(os.path.join('..')) # 親ディレクトリをモジュール探索パスに追加
from bin.AnalysisVSPAERO import *
from bin.AnalysisVSPAERO import *
import openvsp as vsp
if __name__=='__main__':
# Clear the current VSP model and read the new VSP file
vsp.ClearVSPModel()
vsp.Update()
vsp.ReadVSPFile('G103A.vsp3')
vsp.Update()
# Define the list of alpha angles, the Mach number and Reynolds number for the sweep
alpha = [2]
mach = [0.1]
reynolds = [1e6]
# Define the list of height
bref = 17.536552870371967
height = list((1-np.cos(np.linspace(0,1,12)*np.pi/2))*bref)[1:] + [999]
df = vsp_sweep_wig(vsp, alpha, mach, reynolds, height, AnalysisMethod=0, verbose=1)
df = make_CDo_correction(vsp, df, Weight=580, xTr=(0.5, 0.7), CDpCL=0.0016, thickness=0.19, interference_factor=1.14, altitude=0, dT=0)
# Output the results to file
df.to_csv('G103A_DegenGeom.polar', sep='\t')解析結果をG103A_DegenGeom.polarに書き出す前に、有害抗力に対する補正↓を行っている
それでは説明していく
プログラムの解説
↓基本的には、これをベースにして地面効果の設定を追加しているだけである
# Ground Effect
vsp.SetIntAnalysisInput(analysis_name, 'GroundEffectToggle', [1], 0)
vsp.SetDoubleAnalysisInput(analysis_name, 'GroundEffect', [he], 0)vsp.SetIntAnalysisInput( analysis, name, indata, index=0)実行する解析に整数の入力値を設定する関数
引数analysis：実行する解析の名前 [str]name：入力の名前 [str]indata：整数の入力値の配列 [list <int>]index：データのインデックス [int]
↓使い方の例
↓今回はGUIでいうところのこれを設定している
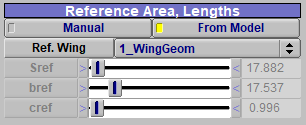
vsp.SetDoubleAnalysisInput(analysis_name, name, indata, index)特定の解析に対してDouble型の入力の値を設定する関数
引数analysis_name：特定の解析の名前 [str]name：入力名 [str]indata：入力の値の配列 [Array of double]index：データのインデックス [int]
↓使い方の例
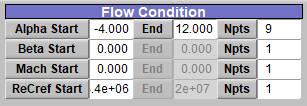
↓今回はGUIでいうところのこれを設定している
↓参考
ただし、VSPAEROSweepで地面効果の計算を有効にしたことで、以下の変更を加えた
- α、Mach、Re数のスイープ計算ができなくなってしまう仕様なので、α、Mach、Re数のリストを1つずつfor文で回して解析し、結果を1つのデータフレームに結合している（なので普通のスイープ計算よりも時間がかかる）
- 書き出された結果のαが必ずゼロになってしまう仕様なので、αの値を上書きしている
- 高度の情報が書き出されないので、追加で書き出している
df = pd.DataFrame()
for re in reynolds:
for ma in mach:
for he in height:
for al in alpha:
:
rid = vsp.ExecAnalysis(analysis_name)
:
tmp = get_polar_result(rid)
bref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'bref')[0] # [m]
tmp['Alpha'], tmp['Height'], tmp['H_bref'] = al, he, he/bref
df = pd.concat([df, tmp])def get_polar_result(result_ids):
# Loop through the results associated with the given result_ids
for result_id in vsp.GetStringResults(result_ids, 'ResultsVec'):
# Check if the result name is 'VSPAERO_Polar'
if vsp.GetResultsName(result_id) == 'VSPAERO_Polar':
data, columns = [], []
# Loop through all available data names for this result_id
for data_name in vsp.GetAllDataNames(result_id):
# Get double results for the data_name and append if available
double_results = vsp.GetDoubleResults(result_id, data_name, 0)
if double_results:
data.append(double_results)
columns.append(data_name)
# If data was found, return it as a pandas DataFrame
if data:
return pd.DataFrame(np.array(data).T, columns=columns)
# Return an empty DataFrame if no data is found
return pd.DataFrame()OpenVSPの解析IDからスイープ計算の結果を取得する関数
引数result_ids：OpenVSPの解析ID（vsp.ExecAnalysisの返値）[list of str]
返値data：スイープ計算の結果 [pd.DataFrame]
VSPAEROの解析が失敗したときは空のデータフレームを返す
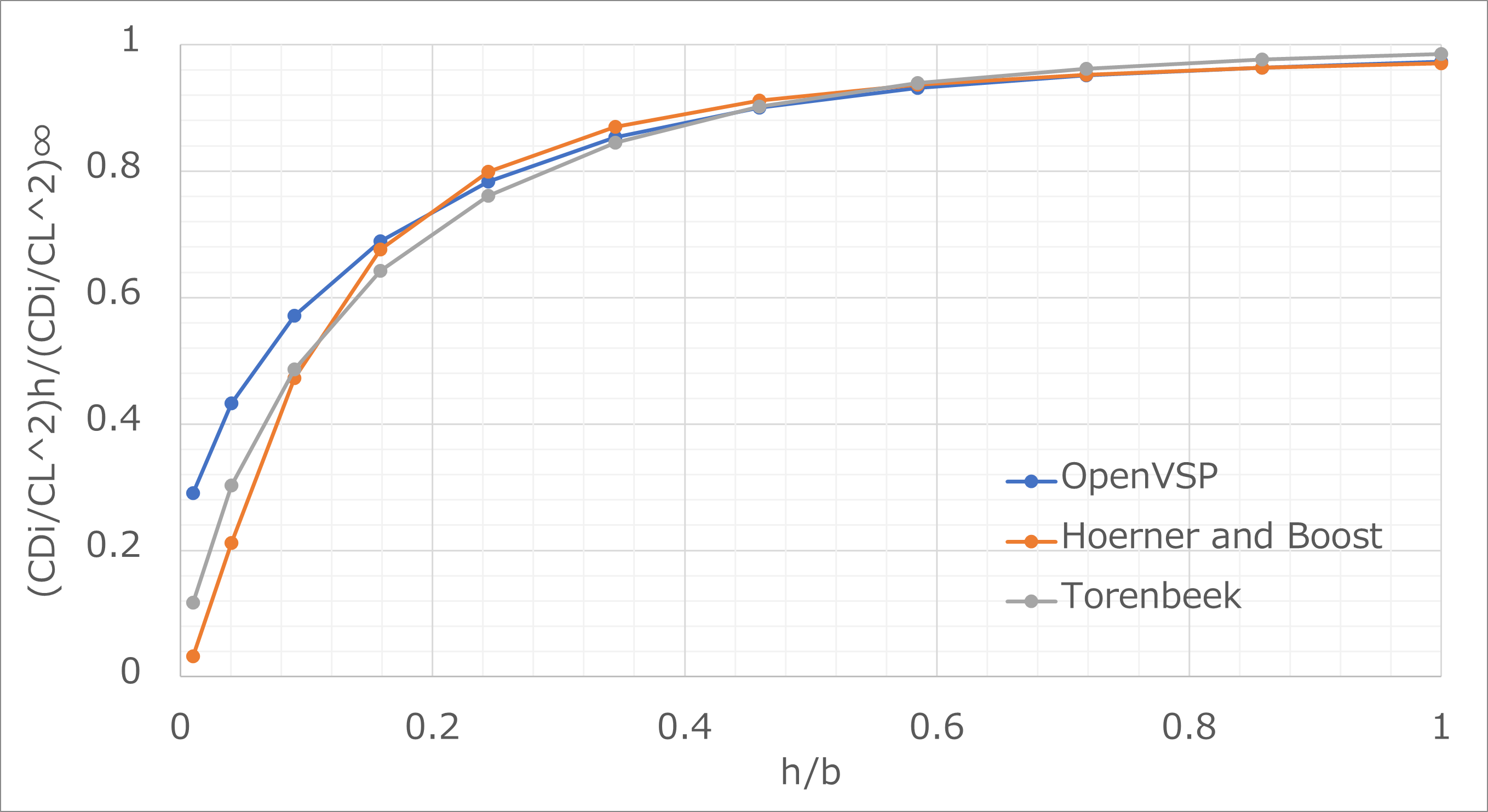
結果の比較
解析した結果をみんな大好きHoerner and Boostの式(1)と今回初めて知ったTorenbeekの式(2)と比較してみる
\begin{align}
\frac{(C_{D_{i}}/C_{L}^{2})_{h}}{(C_{D_{i}}/C_{L}^{2})_{\infty}}
&=\frac{33(h/b)^{1.5}}{1+33(h/b)^{1.5}} \tag{1} \\\\
\frac{(C_{D_{i}}/C_{L}^{2})_{h}}{(C_{D_{i}}/C_{L}^{2})_{\infty}}
&=1-\exp{\left[-2.48 \left(\frac{2h}{b}\right)^{0.768}\right]} \tag{2} \\\\
\end{align}
Hoerner and Borstの式(1)もTorenbeekの式(2)も、高度5m以上の範囲ではよく一致するが，5m以下では誘導抗力が小さくなりすぎ，高度0mで誘導抗力が0になってしまう仕様である
↓参考
グラフで比較するとこんな感じ
VSPAEROの地面効果はきちんと計算できてそうである
おわりに
OpenVSPのPythonAPIで地面効果を計算した
水平尾翼や胴体も含めて地面効果を計算できるのがOpenVSPの良いところだと思う
↓関連記事
コメント