OpenVSPのPython APIでトリムドポーラーを計算する
はじめに
トリムドポーラー(trimed drag polar)とは、エレベータなどを使って常に重心周りのピッチングモーメントがゼロ(トリム状態)になるようにして計算したポーラーカーブである
「そのCLでトリム飛行をしたときにどのくらいのCDが生じるのか」を見るためのグラフであり、航空機の巡航時の性能を見たいときに役に立つ
さらに、機体重量や大気諸元を与えれば、グライダーポーラー(glider polar / flight polar)も計算することができる
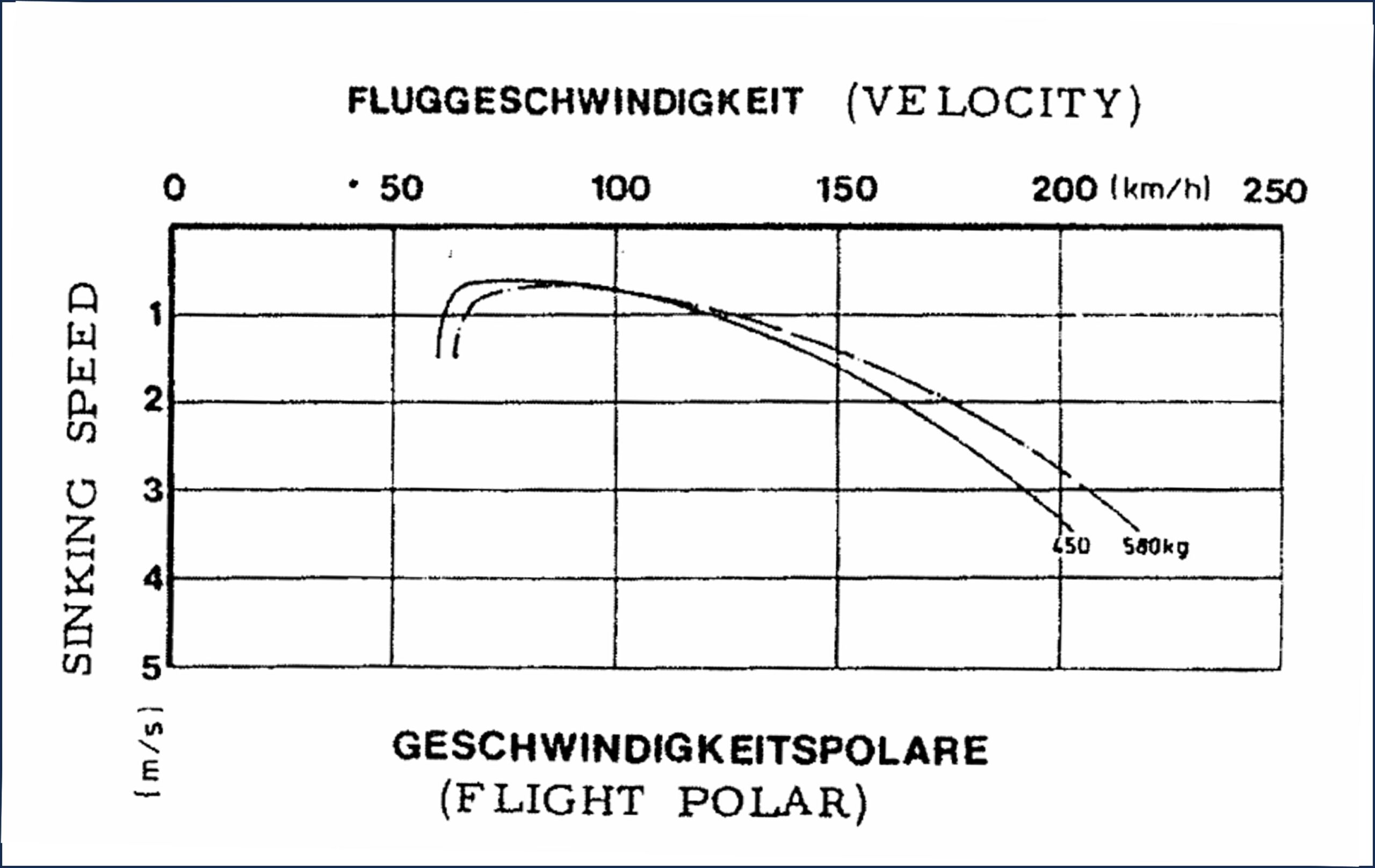
一方、OpenVSPは、普通のスイープ計算や舵角を設定した計算はできるものの、それらを組み合わせてトリムドポーラーを計算する機能は実装されていない
というわけで、Python APIを用いてトリムドポーラーを計算するプログラムを作成する
↓関連記事
ソースコード
ソースコードはこれ
def get_polar_result(result_ids):
# Loop through the results associated with the given result_ids
for result_id in vsp.GetStringResults(result_ids, 'ResultsVec'):
# Check if the result name is 'VSPAERO_Polar'
if vsp.GetResultsName(result_id) == 'VSPAERO_Polar':
data, columns = [], []
# Loop through all available data names for this result_id
for data_name in vsp.GetAllDataNames(result_id):
# Get double results for the data_name and append if available
double_results = vsp.GetDoubleResults(result_id, data_name, 0)
if double_results:
data.append(double_results)
columns.append(data_name)
# If data was found, return it as a pandas DataFrame
if data:
return pd.DataFrame(np.array(data).T, columns=columns)
# Return an empty DataFrame if no data is found
return pd.DataFrame()
def _get_trim(x, vsp, alpha, mach, reynolds, CMy_tol=5e-4):
# Set the elevator deflection and control surface parameters
_ = set_control_surface(geom_name='HTailGeom', deflection=x, cs_group_name='Elevator_Group', gains=(1,-1), verbose=0)
# Perform a sweep analysis with the given alpha and mach
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[mach], reynolds=[reynolds], verbose=0)
# Retrieve polar results from the sweep analysis
df = get_polar_result(result_ids)
# Get the CMy (moment coefficient about the y-axis) value
if list(df.columns):
CMy = df['CMy'].values[0]
f = np.abs(CMy)
# Print the current deflection (x) and CMy value
print(f'\rx = {x:8.4f} ', f'CMy = {CMy:10.6f}', end='')
# If the absolute value of CMy is smaller than the tolerance, raise StopIteration to exit
if f < CMy_tol:
raise StopIteration(x)
# Return the absolute value of CMy to be minimized
return f
else:
raise StopIteration(999)
# return None
def vsp_trimed_sweep(vsp, alpha_list, Weight, altitude=0, dT=0):
g = get_gravity() # [m/s^2]
density = get_density(altitude=altitude, dT=dT) # [kg/m^3]
Sref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'Sref')[0] # [m^2]
cref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'cref')[0] # [m]
# Create an empty DataFrame to store trimmed polar results
trimed_polar = pd.DataFrame()
# Iterate over the alpha angles
for alpha in alpha_list:
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[0], verbose=0)
df = get_polar_result(result_ids)
velocity = np.sqrt((2*Weight*g)/(density*Sref*df['CL'].values[0]))
mach = velocity_to_mach(velocity=velocity, dT=0, altitude=0)
reynolds = velocity_to_reynolds(velocity=mach_to_velocity(mach, altitude=altitude, dT=dT), length=cref, altitude=altitude, dT=dT)
try:
# Minimize the absolute CMy to find the optimal elevator deflection (x) for the given alpha
res = minimize_scalar(fun=_get_trim, args=(vsp, alpha, mach, reynolds), method='bounded', bounds=(-20, 20))
de = res.x
except StopIteration as err:
# If StopIteration is raised, use the optimal deflection (err.value) and print 'Done'
if err.value == 999:
print('\tError\t', 'Alpha 'f'{alpha:8.3f}, velocity {velocity:8.3f}, mach {mach:8.3f}, reynolds {reynolds:8.3e}')
de = None
else:
print('\tDone\t', 'Alpha 'f'{alpha:8.3f}, velocity {velocity:8.3f}, mach {mach:8.3f}, reynolds {reynolds:8.3e}')
de = err.value
if de:
# Set the elevator deflection with the optimized value
_ = set_control_surface(geom_name='HTailGeom', deflection=de, cs_group_name='Elevator_Group', gains=(1,-1), verbose=0)
# Perform another sweep with the optimized elevator deflection
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[mach], reynolds=[reynolds], verbose=0)
# Retrieve polar results and add the deflection value to the results DataFrame
df = get_polar_result(result_ids)
df['de'] = de
# Append the results to the trimmed polar DataFrame
trimed_polar = pd.concat([trimed_polar, df])
trimed_polar['gamma'] = np.arctan(1/trimed_polar['L_D'])
trimed_polar['Velocity'] = np.sqrt((2*Weight*g)/(density*Sref*trimed_polar['CL']*np.cos(trimed_polar['gamma'])))
trimed_polar['Vx'] = trimed_polar['Velocity']*np.cos(trimed_polar['gamma'])*(3.6)
trimed_polar['Vz'] = trimed_polar['Velocity']*np.sin(trimed_polar['gamma'])
return trimed_polar
def make_CDo_correction(vsp, trimed_polar, Weight, CDpCL=0.0065, thickness=0.12, interference_factor=1, xTr=(0,0), altitude=0, dT=0):
# Function to calculate the frictional drag coefficient in turbulent regions
def Cf_turbulance(reynolds):
return 0.455/(np.log10(reynolds)**2.58)
# Function to calculate the frictional drag coefficient in the laminar flow regime
def Cf_laminar(reynolds):
return 1.32824 / np.sqrt(reynolds)
g = get_gravity()
Sref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'Sref')[0] # Get wing area [m^2]
density = get_density(altitude=altitude, dT=dT) # Get density based on altitude [kg/m^3]
reynolds = trimed_polar['Re_1e6'].values * 1e6 # Get Reynolds number
# Correct drag based on percentage of laminar flow area
CDo = 0
for laminar_persent in xTr:
reynolds_laminar = np.maximum(reynolds * laminar_persent, 1e3) # Reynolds number in laminar flow region
CDo += Cf_turbulance(reynolds) - Cf_turbulance(reynolds_laminar) * laminar_persent + Cf_laminar(reynolds_laminar) * laminar_persent
# form factor
form_factor = 1 + 2 * thickness + 60 * (thickness ** 4)
# Corrected CD0, CDtotal, and lift-drag ratio are calculated and added to the data frame
trimed_polar['CDo_corr'] = CDo * form_factor * interference_factor + CDpCL * (trimed_polar['CL'].values) ** 2
trimed_polar['CDtot_corr'] = trimed_polar['CDo_corr'].values + trimed_polar['CDi'].values
trimed_polar['L_D_corr'] = trimed_polar['CL'].values / trimed_polar['CDtot_corr'].values
# Calculate angle of attack from modified lift-drag ratio
trimed_polar['gamma'] = np.arctan(1/trimed_polar['L_D_corr'].values)
# Calculate velocity
trimed_polar['Velocity'] = np.sqrt((2*Weight*g)/(density*Sref*trimed_polar['CL'].values*np.cos(trimed_polar['gamma'].values)))
# Calculates horizontal velocity (Vx) and vertical velocity (Vz) and adds them to the data frame
trimed_polar['Vx'] = trimed_polar['Velocity'].values*np.cos(trimed_polar['gamma'])*(3.6) # horizontal velocity [km/h]
trimed_polar['Vz'] = trimed_polar['Velocity'].values*np.sin(trimed_polar['gamma'].values) # vertical velocity [m/s]
return trimed_polar # Returns corrected data使い方はこれ
import sys
import os
import numpy as np
# ../bin/AnalysisVSPAERO.py をモジュールとしてインポート
sys.path.append(os.path.join('..')) # 親ディレクトリをモジュール探索パスに追加
from bin.AnalysisVSPAERO import *
from bin.ISAspecification import *
import openvsp as vsp
if __name__=='__main__':
# Clear the current VSP model and read the new VSP file
vsp.ClearVSPModel()
vsp.Update()
vsp.ReadVSPFile('G103A.vsp3')
vsp.Update()
# Define the list of alpha angles and the Mach number for the sweep
alpha_list = [-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12]
mach = 0.1
Weight = 580 # [kg]
trimed_polar = vsp_trimed_sweep(vsp=vsp, alpha_list=alpha_list, Weight=Weight)
trimed_polar = make_CDo_correction(vsp, trimed_polar, Weight=Weight, xTr=(0.5, 0.7), CDpCL=0.0016, thickness=0.19, interference_factor=1.14, altitude=0, dT=0)
trimed_polar.to_csv('G103A_DegenGeom_trimed.polar', index=False)最終的にはこんな感じになる
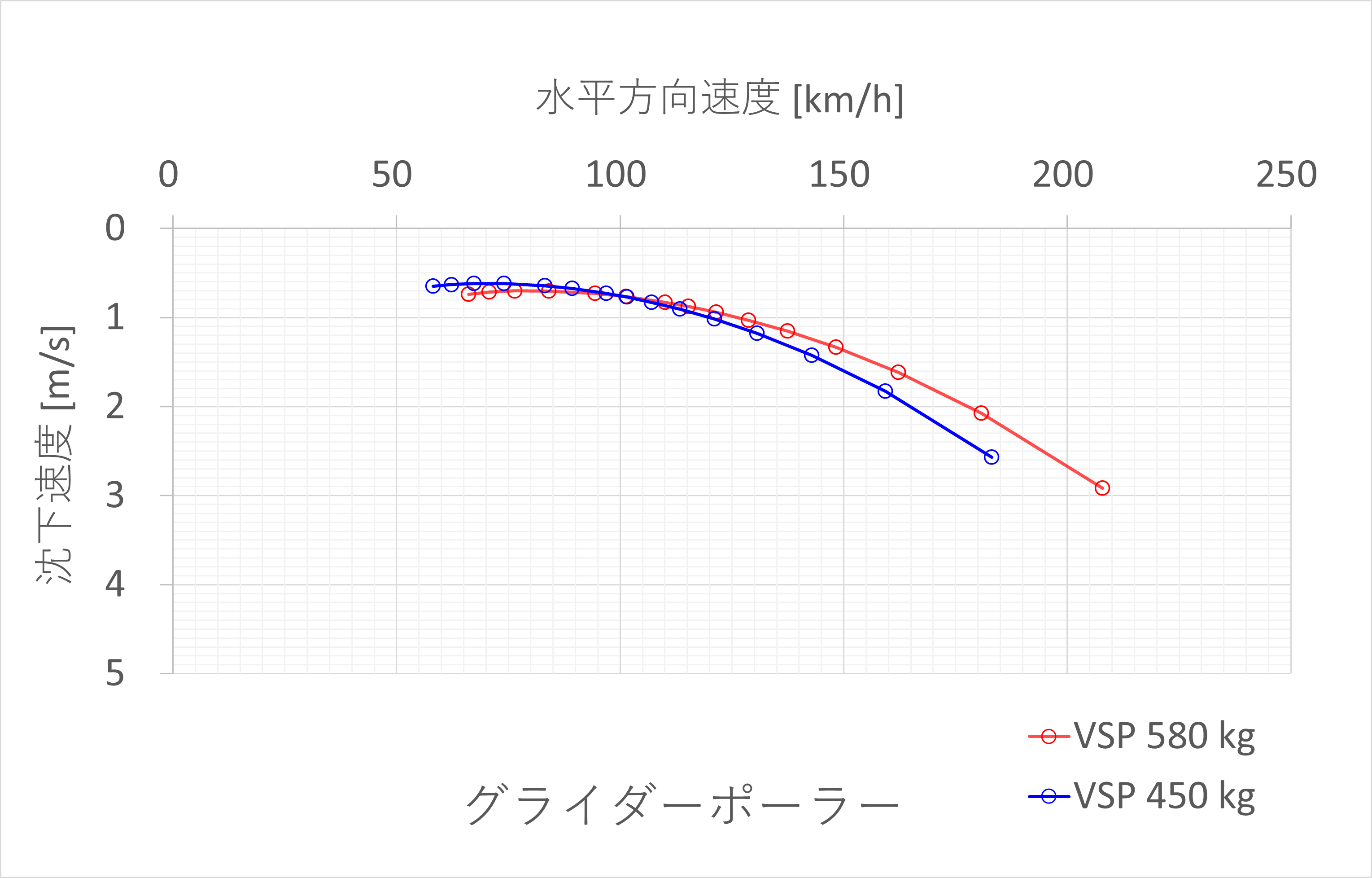
↓なお、大気諸元は国際標準大気に基づいて計算する
プログラムの解説
フローチャートはこれ
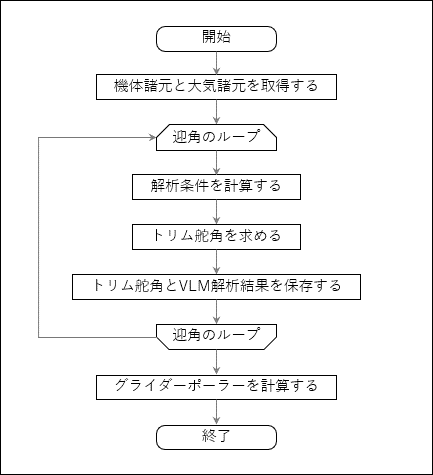
それでは1つずつ説明していく
機体諸元と大気諸元
g = get_gravity() # [m/s^2]
density = get_density(altitude=altitude, dT=dT) # [kg/m^3]
Sref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'Sref')[0] # [m^2]
cref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'cref')[0] # [m]引数から機体諸元と大気諸元を取得する
解析条件
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[0], verbose=0)
df = get_polar_result(result_ids)
velocity = np.sqrt((2*Weight*g)/(density*Sref*df['CL'].values[0]))
mach = velocity_to_mach(velocity=velocity, dT=0, altitude=0)
reynolds = velocity_to_reynolds(velocity=mach_to_velocity(mach, altitude=altitude, dT=dT), length=cref, altitude=altitude, dT=dT)舵角ゼロ度のCLを計算し、そのCLにおける釣り合い飛行速度からマッハ数とレイノルズ数を計算する
ちなみに、今回解析した複座グライダーG103Aでは、着陸進入速度(95km/h)と超過禁止速度(250km/h)で約2.5倍の差があるため、このように各迎角ごとにマッハ数とレイノルズ数を計算しなおしている
トリム舵角
try:
# Minimize the absolute CMy to find the optimal elevator deflection (x) for the given alpha
res = minimize_scalar(fun=_get_trim, args=(vsp, alpha, mach, reynolds), method='bounded', bounds=(-20, 20))
de = res.x
except StopIteration as err:
# If StopIteration is raised, use the optimal deflection (err.value) and print 'Done'
if err.value == 999:
print('\tError\t', 'Alpha 'f'{alpha:8.3f}, velocity {velocity:8.3f}, mach {mach:8.3f}, reynolds {reynolds:8.3e}')
de = None
else:
print('\tDone\t', 'Alpha 'f'{alpha:8.3f}, velocity {velocity:8.3f}, mach {mach:8.3f}, reynolds {reynolds:8.3e}')
de = err.valuedef _get_trim(x, vsp, alpha, mach, reynolds, CMy_tol=5e-4):
# Set the elevator deflection and control surface parameters
_ = set_control_surface(geom_name='HTailGeom', deflection=x, cs_group_name='Elevator_Group', gains=(1,-1), verbose=0)
# Perform a sweep analysis with the given alpha and mach
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[mach], reynolds=[reynolds], verbose=0)
# Retrieve polar results from the sweep analysis
df = get_polar_result(result_ids)
# Get the CMy (moment coefficient about the y-axis) value
if list(df.columns):
CMy = df['CMy'].values[0]
f = np.abs(CMy)
# Print the current deflection (x) and CMy value
print(f'\rx = {x:8.4f} ', f'CMy = {CMy:10.6f}', end='')
# If the absolute value of CMy is smaller than the tolerance, raise StopIteration to exit
if f < CMy_tol:
raise StopIteration(x)
# Return the absolute value of CMy to be minimized
return f
else:
raise StopIteration(999)scipy.minimize_scalarを用いてトリム舵角を計算する
scipy.minimize_scalarはデフォルトでは目的関数fあるいは設計変数xの相対誤差でしか終了条件を指定できないため、目的関数fの絶対値がCMy_tolを下回った場合に計算を強制終了できるよう、StopIterationを用いている
正常時はStopIterationはトリム舵角を返すが、スイープ解析でエラーが起きた場合は999を返すようにしている
結果の保存
if de:
# Set the elevator deflection with the optimized value
_ = set_control_surface(geom_name='HTailGeom', deflection=de, cs_group_name='Elevator_Group', gains=(1,-1), verbose=0)
# Perform another sweep with the optimized elevator deflection
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[mach], reynolds=[reynolds], verbose=0)
# Retrieve polar results and add the deflection value to the results DataFrame
df = get_polar_result(result_ids)
df['de'] = de
# Append the results to the trimmed polar DataFrame
trimed_polar = pd.concat([trimed_polar, df])トリム舵角の計算が正常に終了した場合は、トリム舵角とVLMの解析結果を保存する
グライダーポーラーの計算
trimed_polar['gamma'] = np.arctan(1/trimed_polar['L_D'])
trimed_polar['Velocity'] = np.sqrt((2*Weight*g)/(density*Sref*trimed_polar['CL']*np.cos(trimed_polar['gamma'])))
trimed_polar['Vx'] = trimed_polar['Velocity']*np.cos(trimed_polar['gamma'])*(3.6)
trimed_polar['Vz'] = trimed_polar['Velocity']*np.sin(trimed_polar['gamma'])各迎角ごとに、L/Dから滑空角γを計算し、水平方向速度Vxと沈下速度Vzを計算する
\begin{align}
\gamma &= \arctan{\frac{1}{L/D}} \\\\
V_{x} &= V \cos{\gamma} \\\\
V_{z} &= V \sin{\gamma}
\end{align}
横軸をVx、縦軸を下向きにVzとすればグライダーポーラーの完成である
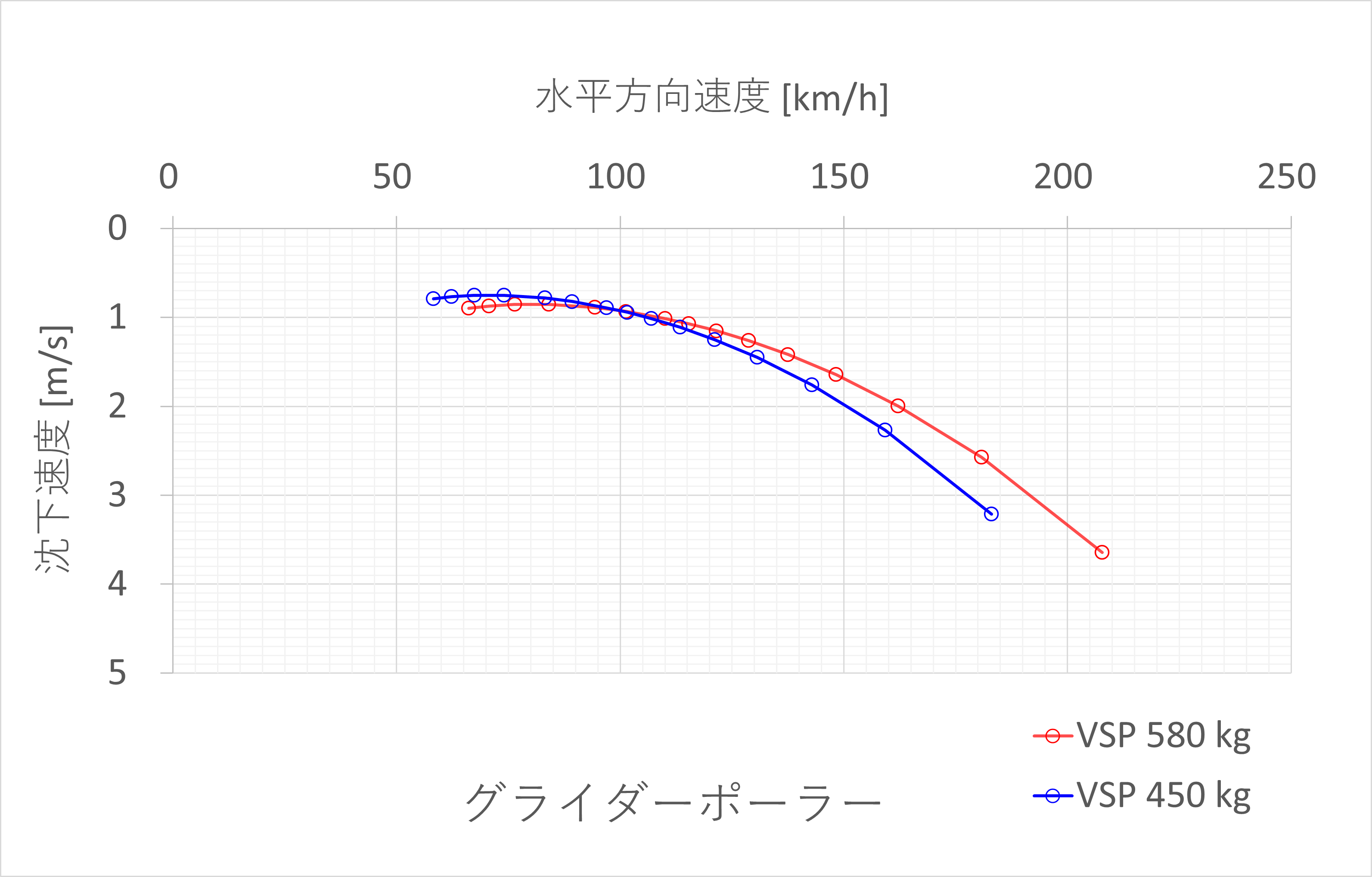
以上
有害抗力係数CDoの補正
↓の記事でも説明したとおり、OpenVSPのVSPAEROの計算では、完全に発達した乱流に対する平板の摩擦抗力とNACA0012の圧力抗力をベースに2次元翼型の有害抗力係数を推算している
一方、今回計算している複座グライダーG103Aのレイノルズ数は2.0×106程度であり、流れは完全に発達した乱流どころかむしろ層流翼に近い
XFLR5の解析結果を見てみると、今回の翼型E603の乱流遷移位置はRe=0.5×106~2.0×106の範囲において、上面が50%付近、下面が70%付近であり、OpenVSPが仮定している完全に発達した乱流(要するに翼前縁での強制乱流遷移)はかなり摩擦抗力を大きく見積もってしまっていると思われる
(OpenVSPは翼の上下面全体を摩擦抗力の大きい乱流境界層だと仮定しているが、XFLR5の計算では上面の50%、下面の70%は摩擦抗力の小さい層流境界層である)
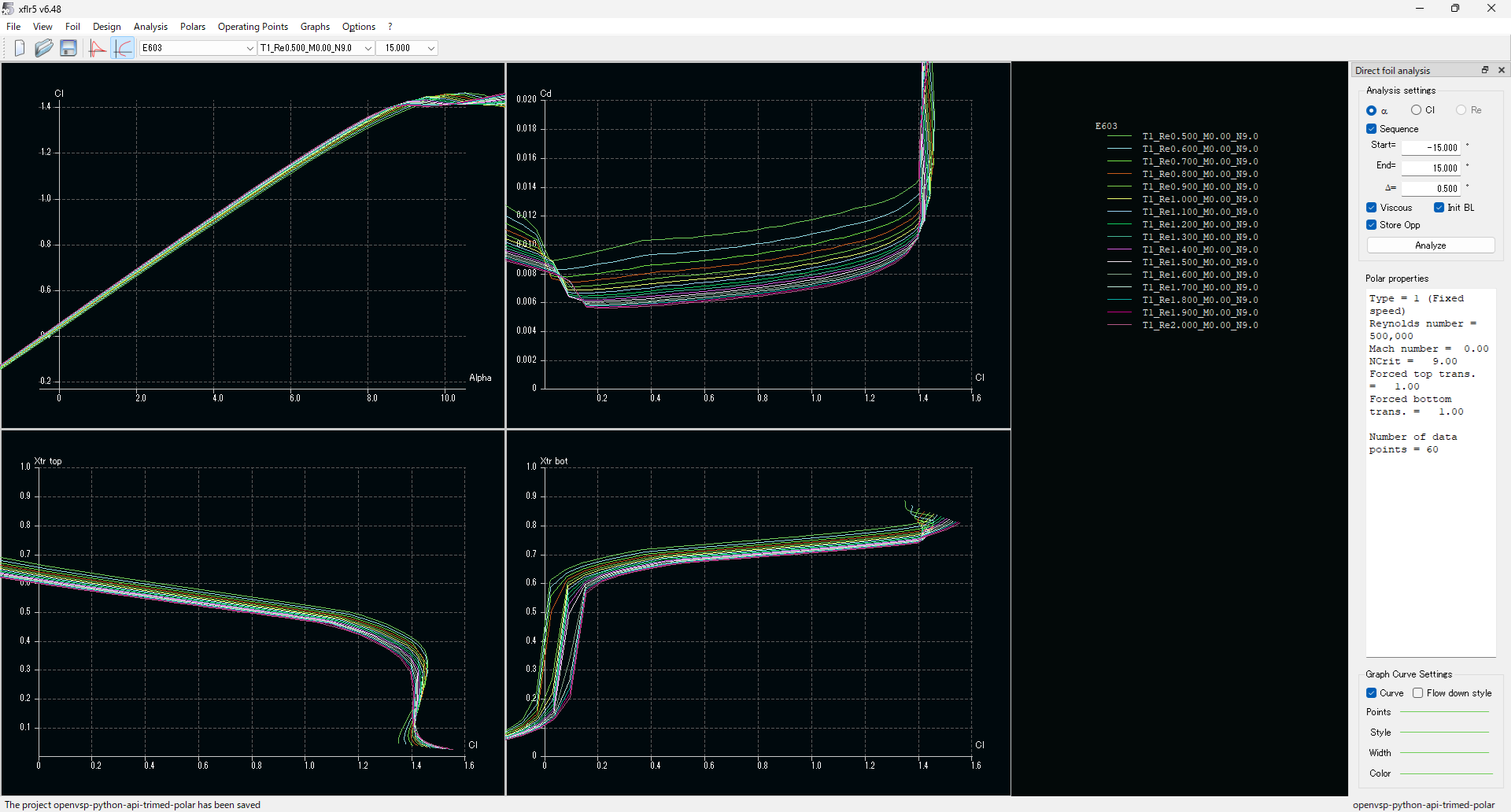
また、主翼翼型に用いられているE603の圧力抗力のcl-cdの形状もNACA0012のそれとは大きく異なる
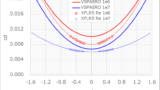
XFLR5の解析結果を見てみると、今回使用する翼型E603のcdは、フライトに使用する cl = 0.2 ~ 1.5 の範囲において抗力の増加量がかなり少なく、OpenVSPが仮定しているNACA0012と同程度の圧力抗力は、今回使用する翼型に対してかなり大きめに見積もられていると思われる
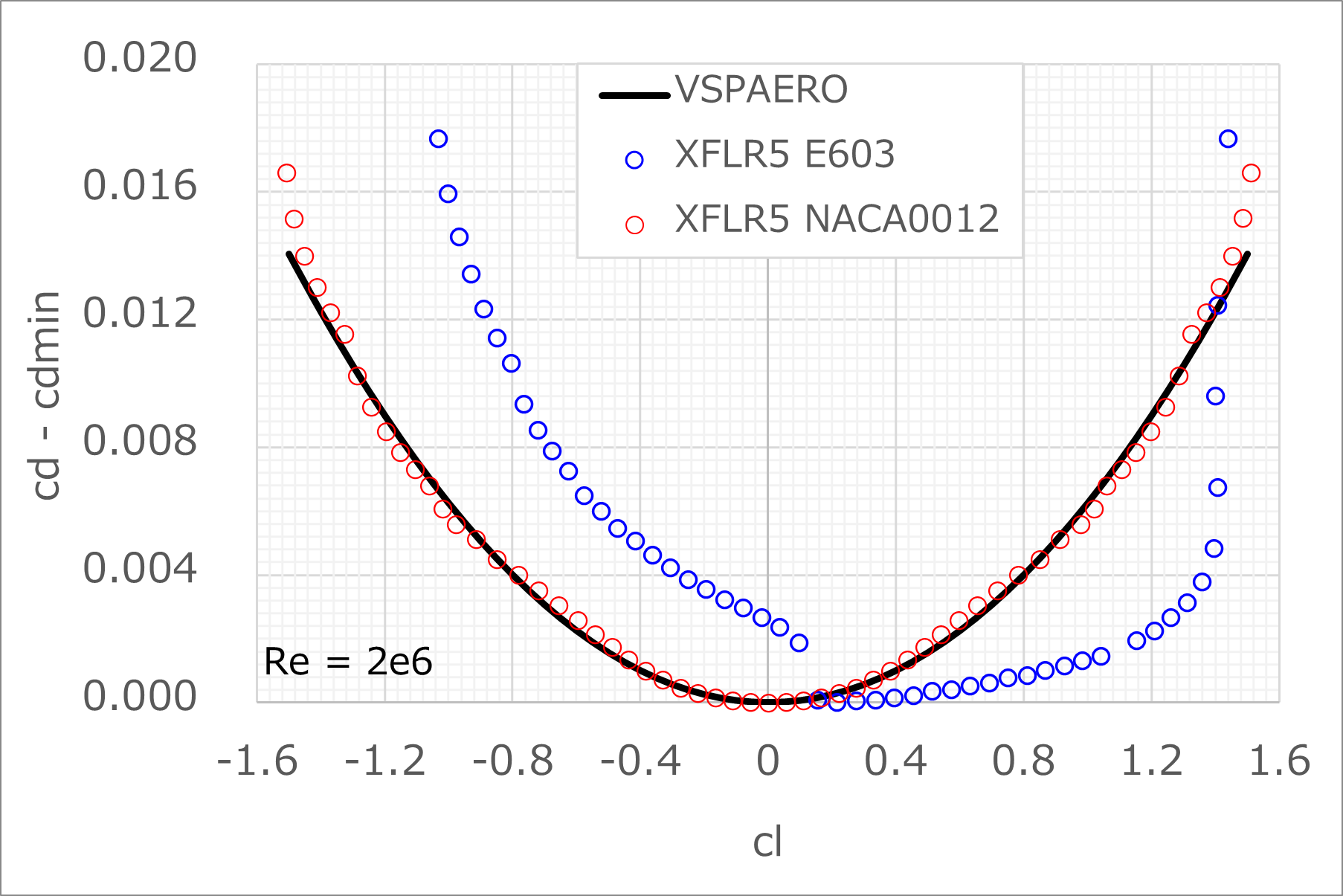
このように、OpenVSPは摩擦抗力と圧力抗力ともに実際より大きめに見積もってしまっているので、現時点で得られたトリムドポーラーを用いて計算したグライダーポーラーと、G103Aの飛行規程に記されている実際のグライダーポーラを比較してもいまいち一致しない(実際よりも抗力が大きすぎて性能が悪い)
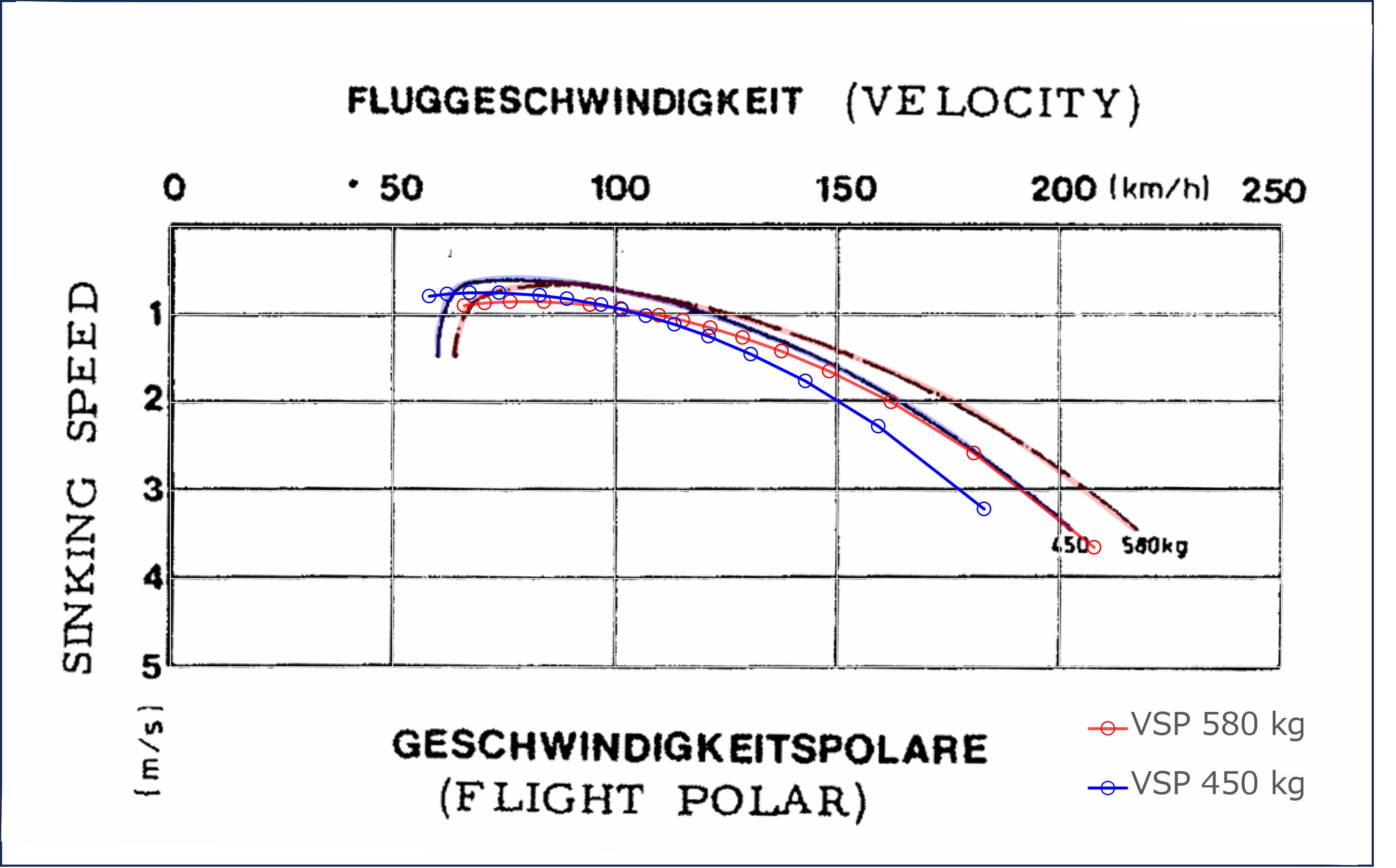
よって、よりそれっぽい結果を得るために、有害抗力の補正を試みる
摩擦抗力
摩擦抗力はOpenVSPのParasite Drag Toolと同じやり方で計算する
↓参考
2次元翼の摩擦抗力は、摩擦抗力係数 \(C_{f}\)、形状係数 \(FF\)、干渉抗力係数 \(Q\) を用いて次の式で計算する
\begin{align}
C_{D_{o}}=C_{f} \times Q \times FF \times 2
\end{align}
OpenVSPのVSPAEROでは完全に発達した乱流(翼前縁で強制乱流遷移)に対する平板の摩擦抗力の式を用いているが、今回は翼面の途中で層流から乱流に遷移しているため、Laminar Parcentを用いて摩擦抗力を計算する
流れに占める層流の割合を\(\%laminar\)とすると、層流と乱流を含む平板の摩擦抗力係数は以下の式で計算する
\begin{align}
C_{f}=C_{f~(100\%turbulance)}-\left(C_{f~(\%partial~turbulance)}-C_{f~(\%partial~laminar)}\right) \times \%laminar
\end{align}
ここで、\(C_{f~(\%partial~laminar)}\)と\(C_{f~(\%partial~turbulance)}\)はそれぞれ\(Re_{laminar}=Re \times \%laminar\) をレイノルズ数として計算した層流、乱流の摩擦抗力係数である
\begin{align}
C_{f~(100\%turbulance)}&=\frac{0.455}{\left(\log_{10}{Re}\right)^{2.58}} \\\\
C_{f~(\%partial~laminar)}&=\frac{1.32824}{\sqrt{Re_{laminar}}} \\\\
C_{f~(\%partial~turbulance)}&=\frac{0.455}{\left(\log_{10}{Re_{laminar}}\right)^{2.58}} \\\\
\end{align}
形状係数は一番有名なHoernerの式を用いて、干渉抗力係数\(Q\)はOpenVSPに用いられている謎係数1.14を用いる
\begin{align}
FF &= 1+2\left(\frac{t}{c}\right)+60\left(\frac{t}{c}\right)^4 \\\\
Q &= 1.14
\end{align}
圧力抗力
圧力抗力の補正式を得るために、XFLR5を用いて計算したG103Aの翼型E603の解析結果を用いて、Re=2.0×106における圧力抗力cdpを揚力係数clの二次関数で以下のように近似する
\begin{align}
c_{D_{p}}=c_{d}-\min{\left(c_{d}\right)}=0.0013 \times c_{l}^{2}
\end{align}
グラフで見るとこんな感じ
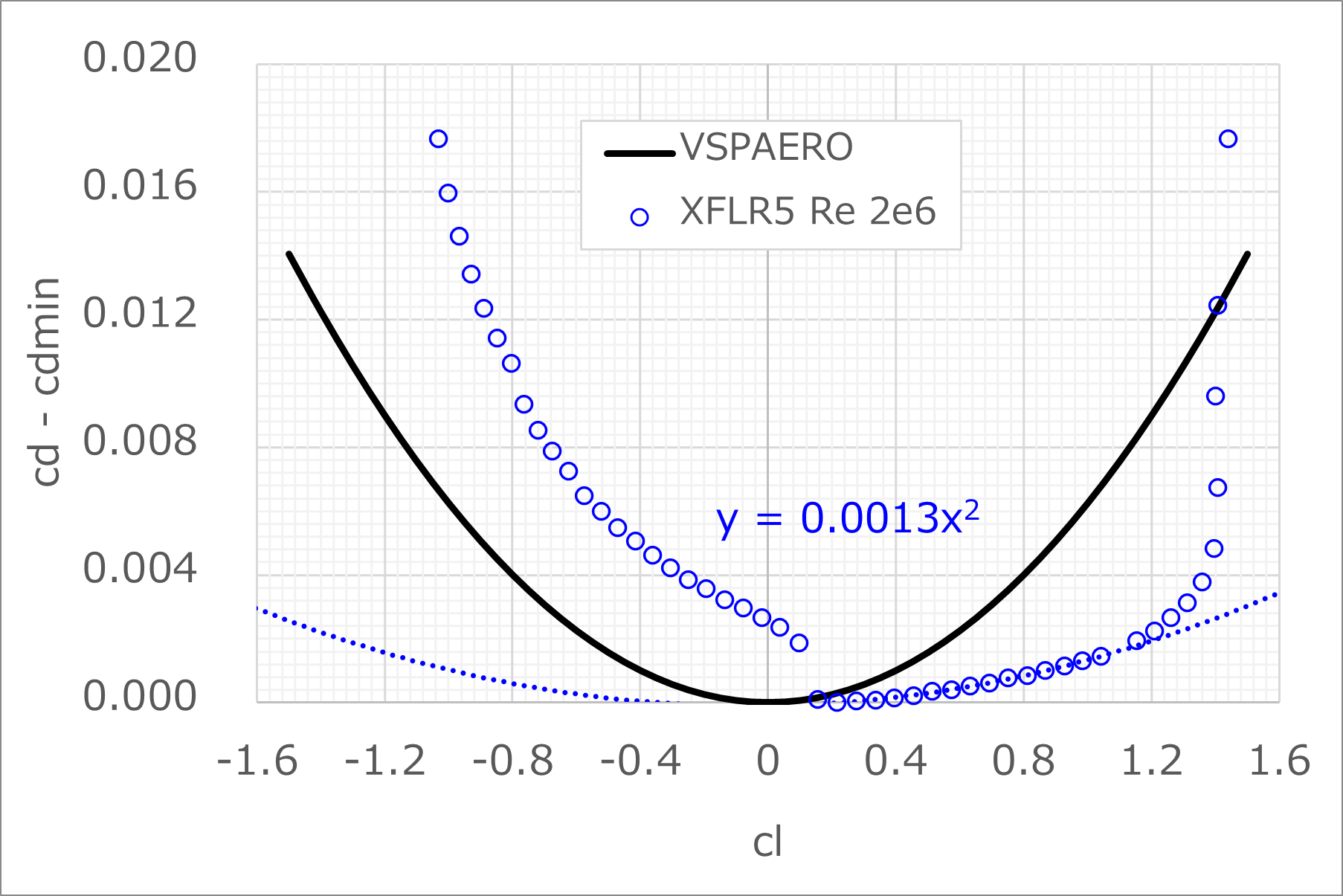
OpenVSPのVSPAEROでデフォルトで用いられているNACA0012の圧力抗力とは大きく異なることがわかる
有害抗力の補正
まとめると、有害抗力係数CDoは以下の式で補正する
\begin{align}
C_{D_{o}} &= C_{f} \times Q \times FF \times 2 + 0.0013 \times c_{l}^{2}
\end{align}
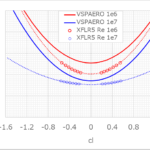
補正後の結果はこんな感じ
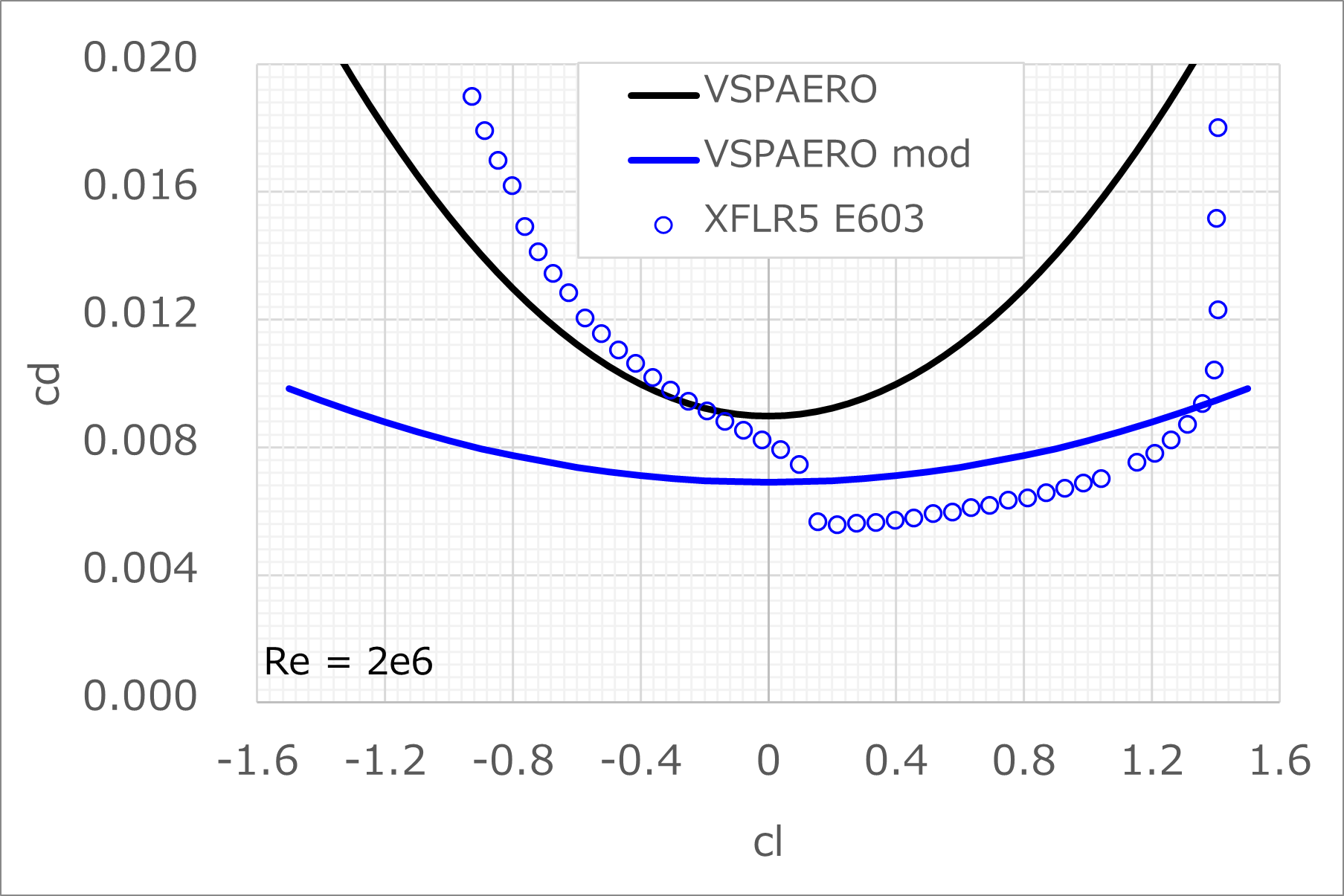
干渉抗力係数1.14の分だけXFLR5の結果よりも大きくなっているが、それ以外はなんとなく良い感じに見える
使い方
上記のソースコードを以下に示す関数にまとめる
def vsp_trimed_sweep(vsp, alpha_list, Weight, altitude=0, dT=0):
g = get_gravity() # [m/s^2]
density = get_density(altitude=altitude, dT=dT) # [kg/m^3]
Sref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'Sref')[0] # [m^2]
cref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'cref')[0] # [m]
# Create an empty DataFrame to store trimmed polar results
trimed_polar = pd.DataFrame()
# Iterate over the alpha angles
for alpha in alpha_list:
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[0], verbose=0)
df = get_polar_result(result_ids)
velocity = np.sqrt((2*Weight*g)/(density*Sref*df['CL'].values[0]))
mach = velocity_to_mach(velocity=velocity, dT=0, altitude=0)
reynolds = velocity_to_reynolds(velocity=mach_to_velocity(mach, altitude=altitude, dT=dT), length=cref, altitude=altitude, dT=dT)
try:
# Minimize the absolute CMy to find the optimal elevator deflection (x) for the given alpha
res = minimize_scalar(fun=_get_trim, args=(vsp, alpha, mach, reynolds), method='bounded', bounds=(-20, 20))
de = res.x
except StopIteration as err:
# If StopIteration is raised, use the optimal deflection (err.value) and print 'Done'
if err.value == 999:
print('\tError\t', 'Alpha 'f'{alpha:8.3f}, velocity {velocity:8.3f}, mach {mach:8.3f}, reynolds {reynolds:8.3e}')
de = None
else:
print('\tDone\t', 'Alpha 'f'{alpha:8.3f}, velocity {velocity:8.3f}, mach {mach:8.3f}, reynolds {reynolds:8.3e}')
de = err.value
if de:
# Set the elevator deflection with the optimized value
_ = set_control_surface(geom_name='HTailGeom', deflection=de, cs_group_name='Elevator_Group', gains=(1,-1), verbose=0)
# Perform another sweep with the optimized elevator deflection
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[mach], reynolds=[reynolds], verbose=0)
# Retrieve polar results and add the deflection value to the results DataFrame
df = get_polar_result(result_ids)
df['de'] = de
# Append the results to the trimmed polar DataFrame
trimed_polar = pd.concat([trimed_polar, df])
trimed_polar['gamma'] = np.arctan(1/trimed_polar['L_D'])
trimed_polar['Velocity'] = np.sqrt((2*Weight*g)/(density*Sref*trimed_polar['CL']*np.cos(trimed_polar['gamma'])))
trimed_polar['Vx'] = trimed_polar['Velocity']*np.cos(trimed_polar['gamma'])*(3.6)
trimed_polar['Vz'] = trimed_polar['Velocity']*np.sin(trimed_polar['gamma'])
return trimed_polarトリムドポーラーを計算する関数
引数vsp:OpenVSPのオブジェクトalpha_list:トリムドポーラーを計算する迎角(deg)のリスト [list of float]Weight:機体重量(kg) [float]altitude=0:高度(m) [float]dT=0:海面上の気温15℃との温度差(℃) [float]
返値trimed_polar:トリムドポーラの結果 [DataFrame]
def _get_trim(x, vsp, alpha, mach, reynolds, CMy_tol=5e-4):
# Set the elevator deflection and control surface parameters
_ = set_control_surface(geom_name='HTailGeom', deflection=x, cs_group_name='Elevator_Group', gains=(1,-1), verbose=0)
# Perform a sweep analysis with the given alpha and mach
result_ids = vsp_sweep(vsp=vsp, alpha=[alpha], mach=[mach], reynolds=[reynolds], verbose=0)
# Retrieve polar results from the sweep analysis
df = get_polar_result(result_ids)
# Get the CMy (moment coefficient about the y-axis) value
if list(df.columns):
CMy = df['CMy'].values[0]
f = np.abs(CMy)
# Print the current deflection (x) and CMy value
print(f'\rx = {x:8.4f} ', f'CMy = {CMy:10.6f}', end='')
# If the absolute value of CMy is smaller than the tolerance, raise StopIteration to exit
if f < CMy_tol:
raise StopIteration(x)
# Return the absolute value of CMy to be minimized
return f
else:
raise StopIteration(999)トリム舵角を求めるときにscipy.minimize_scalarから呼び出される内部関数
引数x:トリム舵角(deg) [float]vsp:OpenVSPのオブジェクトalpha:迎角(deg) [float]mach:マッハ数 [float]reynolds:レイノルズ数 [float]CMy_tol=5e-4:トリムが取れたとみなす|Cmcg|の閾値 [float]
返値f:重心周りのピッチングモーメントの絶対値|Cmcg| [flaot]
scipy.minimize_scalarはデフォルトではfおよびxの相対誤差でしか終了条件を指定できないため、fの値がCMy_tolを下回った場合に計算を強制終了するためにStopIterationを用いている
↓公式ドキュメント
def get_polar_result(result_ids):
# Loop through the results associated with the given result_ids
for result_id in vsp.GetStringResults(result_ids, 'ResultsVec'):
# Check if the result name is 'VSPAERO_Polar'
if vsp.GetResultsName(result_id) == 'VSPAERO_Polar':
data, columns = [], []
# Loop through all available data names for this result_id
for data_name in vsp.GetAllDataNames(result_id):
# Get double results for the data_name and append if available
double_results = vsp.GetDoubleResults(result_id, data_name, 0)
if double_results:
data.append(double_results)
columns.append(data_name)
# If data was found, return it as a pandas DataFrame
if data:
return pd.DataFrame(np.array(data).T, columns=columns)
# Return an empty DataFrame if no data is found
return pd.DataFrame()OpenVSPの解析IDからスイープ計算の結果を取得する関数
引数result_ids:OpenVSPの解析ID(vsp.ExecAnalysisの返値)[list of str]
返値data:スイープ計算の結果 [pd.DataFrame]
VSPAEROの解析が失敗したときは空のデータフレームを返す
def make_CDo_correction(vsp, trimed_polar, Weight, CDpCL=0.0065, thickness=0.12, interference_factor=1, xTr=(0,0), altitude=0, dT=0):
# 乱流領域の摩擦抗力係数を計算する関数
def Cf_turbulance(reynolds):
return 0.455/(np.log10(reynolds)**2.58)
# 層流領域の摩擦抗力係数を計算する関数
def Cf_laminar(reynolds):
return 1.32824 / np.sqrt(reynolds)
g = get_gravity()
Sref = vsp.GetDoubleAnalysisInput('VSPAEROSweep', 'Sref')[0] # 翼面積を取得 [m^2]
density = get_density(altitude=altitude, dT=dT) # 高度に基づく密度を取得 [kg/m^3]
reynolds = trimed_polar['Re_1e6'].values * 1e6 # レイノルズ数を取得
# 層流領域の割合に基づいて抗力を補正
CDo = 0
for laminar_persent in xTr:
# 乱流から層流への遷移によるCD0の補正
reynolds_laminar = np.maximum(reynolds * laminar_persent, 1e3) # 層流領域のレイノルズ数
CDo += Cf_turbulance(reynolds) - Cf_turbulance(reynolds_laminar) * laminar_persent + Cf_laminar(reynolds_laminar) * laminar_persent
# 形状係数
form_factor = 1 + 2 * thickness + 60 * (thickness ** 4)
# 補正後のCD0、CDtotal、揚抗比を計算し、データフレームに追加
trimed_polar['CDo_corr'] = CDo * form_factor * interference_factor + CDpCL * (trimed_polar['CL'].values) ** 2
trimed_polar['CDtot_corr'] = trimed_polar['CDo_corr'].values + trimed_polar['CDi'].values
trimed_polar['L_D_corr'] = trimed_polar['CL'].values / trimed_polar['CDtot_corr'].values
# 修正後の揚抗比から迎え角を計算
trimed_polar['gamma'] = np.arctan(1/trimed_polar['L_D_corr'].values)
# 速度を計算
trimed_polar['Velocity'] = np.sqrt((2*Weight*g)/(density*Sref*trimed_polar['CL'].values*np.cos(trimed_polar['gamma'].values)))
# 水平速度 (Vx) と鉛直速度 (Vz) を計算し、データフレームに追加
trimed_polar['Vx'] = trimed_polar['Velocity'].values*np.cos(trimed_polar['gamma'])*(3.6) # 水平速度 [km/h]
trimed_polar['Vz'] = trimed_polar['Velocity'].values*np.sin(trimed_polar['gamma'].values) # 鉛直速度 [m/s]
return trimed_polar # 補正後のデータを返すトリムドポーラーに対してCD0(ゼロ揚抗係数)の補正を行う関数
引数:vsp : OpenVSPオブジェクト [vsp object]trimed_polar : トリムドポーラー [pd.DataFrame]Weight : 機体の重量(kg) [float]CDpCL : 圧力抗力をCLの二次関数で近似したときの係数 [float]thickness : 翼厚 [float]interference_factor : 干渉抗力係数 [float]xTr : 上下面の層流遷移位置 [tuple of float, (upper, lower)]altitude : 飛行高度(m) [float]dT : ISAからの気温差(℃) [float]
返値:trimed_polar : 補正後のトリムドポーラー [pd.DataFrame]
実行するためのファイルはこれ
import sys
import os
import numpy as np
# ../bin/AnalysisVSPAERO.py をモジュールとしてインポート
sys.path.append(os.path.join('..')) # 親ディレクトリをモジュール探索パスに追加
from bin.AnalysisVSPAERO import *
from bin.ISAspecification import *
import openvsp as vsp
if __name__=='__main__':
# Clear the current VSP model and read the new VSP file
vsp.ClearVSPModel()
vsp.Update()
vsp.ReadVSPFile('G103A.vsp3')
vsp.Update()
# Define the list of alpha angles and the Mach number for the sweep
alpha_list = [-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12]
mach = 0.1
Weight = 580 # [kg]
trimed_polar = vsp_trimed_sweep(vsp=vsp, alpha_list=alpha_list, Weight=Weight)
trimed_polar = make_CDo_correction(vsp, trimed_polar, Weight=Weight, xTr=(0.2, 0.30), CDpCL=0.0016, thickness=0.19, interference_factor = 1.14, altitude=0, dT=0)
trimed_polar.to_csv('G103A_DegenGeom_trimed.polar', index=False)ターミナルなどで上記のプログラム(test_trimed_polar.py)を実行すると1迎角当たり1分ほどでトリムドポーラーが計算され、G103A_DegenGeom_trimed.polarというファイルに出力される
Alpha,Beta,CDi,CDo,CDt,CDtot,CDtott,CFx,CFy,CFz,CL,CMl,CMm,CMn,CMx,CMy,CMz,CS,E,Fopt,L_D,Mach,Re_1e6,de,gamma,Velocity,Vx,Vz,CDo_corr,CDtot_corr,L_D_corr
-2.0,0.0,0.000401346338,0.01054549818,0.000751495149,0.010946844517,0.011296993329,0.016369131397,0.0,0.155082902584,0.155559704718,-0.0,-0.000370143781,-0.0,0.0,-0.000370143781,0.0,-4.2608772e-05,0.040914716318,0.0,14.21046078342,0.072278,1.683793614065,0.2584914830922706,0.04941109515745192,57.81352935629875,207.87468879749653,2.8554675528178897,0.007291290465950853,0.007692636803950853,20.221896429336983
-1.5,0.0,0.000750843463,0.010969575813,0.001057134616,0.011720419276,0.012026710429,0.017099051508,0.0,0.205248249375,0.205625516914,-0.0,-0.000214483323,-0.0,0.0,-0.000214483323,0.0,-3.7564676e-05,0.06677057864,0.0,17.544211693663,0.062197,1.448958690512,-0.04706157887029416,0.040800443366865564,50.27535415590594,180.84064992614833,2.0506876743160625,0.007643427225793711,0.008394270688793712,24.495935923118193
-1.0,0.0,0.00119653082,0.011349403754,0.001449039283,0.012545934574,0.012798443037,0.017006271729,0.0,0.255423057733,0.255680955931,-0.0,-4.9846128e-05,-0.0,0.0,-4.9846128e-05,0.0,-3.1791663e-05,0.096442401936,0.0,20.379586264733,0.055818,1.300344556151,-0.35486590493903564,0.035662871028382996,45.081855116567816,162.1914828957684,1.607407606530486,0.007925653784609181,0.00912218460460918,28.02847859511763
-0.5,0.0,0.001741373608,0.011724661831,0.001938659128,0.01346603544,0.01366332096,0.016134712467,0.0,0.305741341136,0.305870499584,-0.0,-0.000206208062,-0.0,0.0,-0.000206208062,0.0,-2.5612476e-05,0.128590742962,0.0,22.714220600047,0.051067,1.18966178994,-0.6531504026882093,0.03242711352866556,41.21527888963213,148.29700136726606,1.3362583157276526,0.008180601761775715,0.009921975369775715,30.827581019374588
0.0,0.0,0.002384252037,0.012103316528,0.002519119363,0.014487568565,0.014622435891,0.014487568565,0.0,0.355878066016,0.355878066016,-0.0,-0.000349184411,-0.0,0.0,-0.000349184411,0.0,-1.8964576e-05,0.161801004315,0.0,24.564374927199,0.047353,1.10314947389,-0.9563223876441556,0.03034368292561598,38.2086967284457,137.48798864760832,1.1592146703742319,0.008417714626219482,0.010801966663219482,32.94567342331827
0.5,0.0,0.003129505581,0.012492932358,0.003208414417,0.01562243794,0.015701346775,0.012080249506,0.0,0.40596275732,0.405841880776,-0.0,0.000298657294,-0.0,0.0,0.000298657294,0.0,-1.2147202e-05,0.19513680484,0.0,25.978140053681,0.04435,1.033192193218,-1.285133904732111,0.028999714387093107,35.77879769160163,128.74951460826045,1.0374294897326615,0.008643093419780033,0.011772599000780034,34.47343112163334
1.0,0.0,0.003972652542,0.012895013774,0.003970365508,0.016867666315,0.016865379282,0.008908512475,0.0,0.456126820053,0.455901874748,-0.0,-5.5037552e-05,-0.0,0.0,-5.5037552e-05,0.0,-4.615869e-06,0.228066778983,0.0,27.028153523005,0.04186,0.975170056469,-1.6000524722029632,0.028142463183471456,33.75694720133474,121.47688930425906,0.9498782485643269,0.008860937422469933,0.012833589964469934,35.524111025065785
1.5,0.0,0.004915160866,0.013314282685,0.004830023311,0.018229443552,0.018144305996,0.004977437582,0.0,0.506312327067,0.506008532352,-0.0,-0.000355383773,-0.0,0.0,-0.000355383773,0.0,3.447324e-06,0.259965993877,0.0,27.757760730446,0.039739,0.925775840128,-1.9201226871650368,0.027640942860587516,32.04179925499965,115.3064149883175,0.8855527687138588,0.009074955162715127,0.013990116028715128,36.1690018376833
2.0,0.0,0.005961556063,0.013749820467,0.005784553157,0.01971137653,0.019534373624,0.000299619496,0.0,0.556224054458,0.555874761223,-0.0,-0.000475033552,-0.0,0.0,-0.000475033552,0.0,1.1962474e-05,0.290142421718,0.0,28.200707362138,0.037919,0.883363248839,-2.253123524831756,0.027422485771178447,30.570745591385954,110.01330656109961,0.8382207707894928,0.009285733809171616,0.015247289872171617,36.457282958694655
3.0,0.0,0.008353552762,0.014682529106,0.007982631425,0.023036081869,0.022665160531,-0.011293591894,0.0,0.655652418533,0.655344930611,-0.0,0.000402803912,-0.0,0.0,0.000402803912,0.0,3.0806895e-05,0.345068685228,0.0,28.448628301889,0.034863,0.812184859605,-2.9644427495615377,0.02755725039954565,28.15531180869555,101.32063878409205,0.7757847801309131,0.009710524452854967,0.018064077214854965,36.278904414341085
4.0,0.0,0.011158492149,0.01569305246,0.010538311303,0.026851544609,0.026231363762,-0.025883572576,0.0,0.755084987473,0.755051185144,-0.0,-0.000159049343,-0.0,0.0,-0.000159049343,0.0,5.2228669e-05,0.392968544087,0.0,28.119469331793,0.032496,0.757037438182,-3.675384074228278,0.028195301201601325,26.23076641060438,94.39322651791446,0.7394863717435449,0.010136046613234183,0.021294538762234184,35.45750361510913
6.0,0.0,0.017988885558,0.017965422114,0.016673676258,0.035954307672,0.034639098372,-0.063847313143,0.0,0.951433278971,0.952895089445,-0.0,8.7731637e-05,-0.0,0.0,8.7731637e-05,0.0,0.000104180482,0.467426705285,0.0,26.502946410315,0.028857,0.672260134953,-5.239296519843865,0.030442966684011967,23.350218366558874,84.02183644311471,0.7107401253220258,0.011029032810135989,0.02901791836813599,32.83816148891491
8.0,0.0,0.026453023186,0.020570625516,0.024325741276,0.047023648702,0.044896366793,-0.113501325018,0.0,1.145482751539,1.150131323509,-0.0,5.9376326e-05,-0.0,0.0,5.9376326e-05,0.0,0.000170308126,0.520658319788,0.0,24.458572553307,0.026287,0.612394479721,-6.845128856650657,0.03340546107098576,21.25496131257451,76.47517060506691,0.7098997330446147,0.011981941875670536,0.03843496506167053,29.924089215732746
10.0,0.0,0.036582881919,0.023489037947,0.033464945266,0.060071919866,0.056953983214,-0.174477445312,0.0,1.335451162523,1.345460349044,-0.0,7.215617e-05,-0.0,0.0,7.215617e-05,0.0,0.000253808692,0.557756408489,0.0,22.397492073603,0.024315,0.566449497669,-8.54281703833605,0.036844665522061594,19.652817693114834,70.70212642839108,0.7239376740803176,0.013012599086887702,0.049595481005887704,27.12868837554523
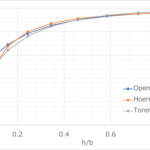
12.0,0.0,0.048356239721,0.02669647861,0.043967988602,0.075052718332,0.070664467212,-0.246501406712,0.0,1.520681577071,1.53870156035,-0.0,0.00022508123,-0.0,0.0,0.00022508123,0.0,0.000356595627,0.58387063781,0.0,20.501609995636,0.022743,0.529832117416,-10.378542046912804,0.04058472197238825,18.378689380899996,66.10879982903815,0.7456892528255235,0.014125844228095201,0.0624820839490952,24.626284257797742グライダーポーラーはこうなる
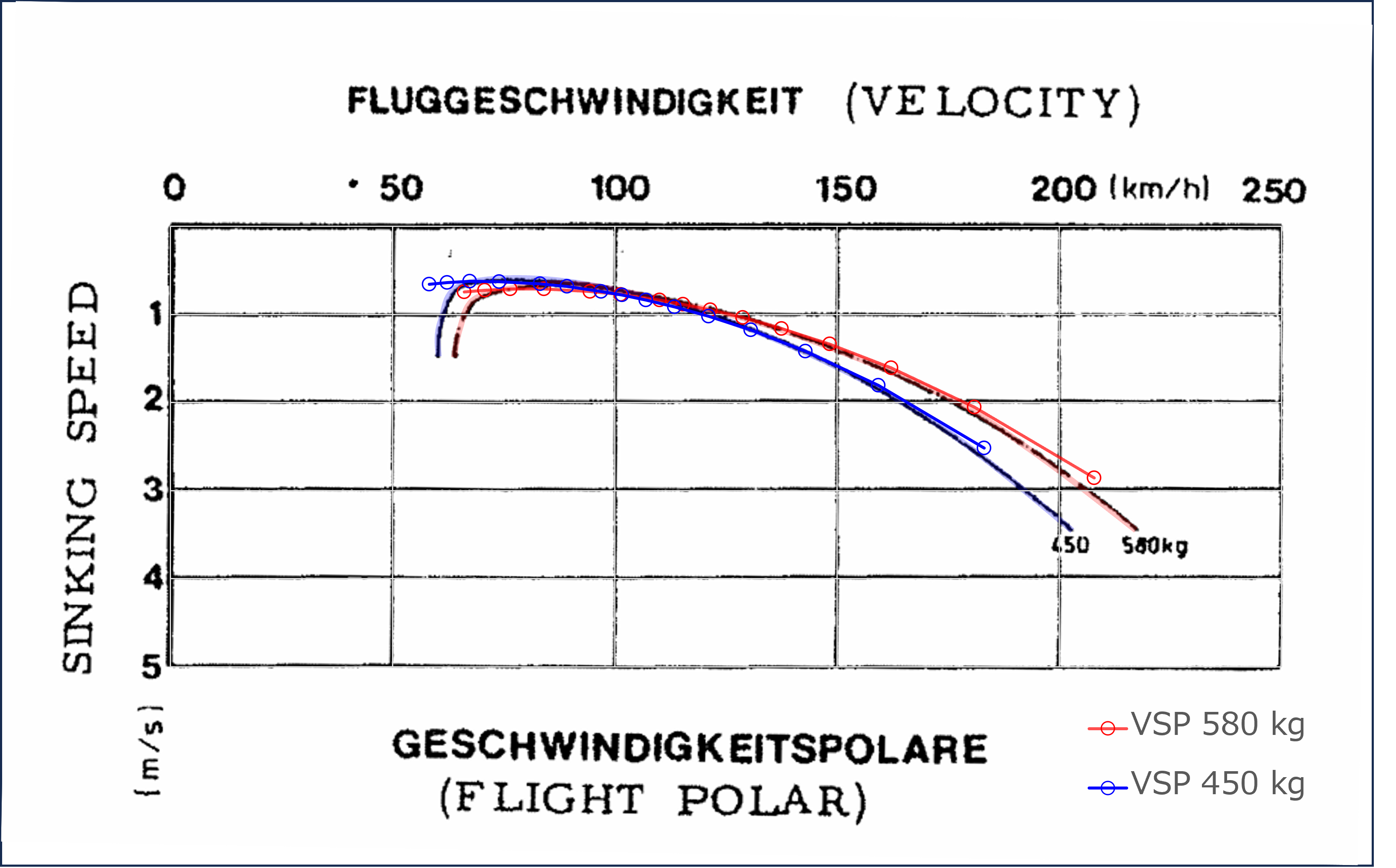
ざっくり推算にしてはそれなりに一致しているのではないだろうか
おわりに
OpenVSPのPython APIでトリムドポーラーを計算した
これでようやくOpenVSPを機体設計に使う最初の一歩が踏み出せた
あとは動安定微係数や地面効果あたりも計算していきたい

コメント