OpenFOAMで実装されているk‐εモデルの壁関数について説明する
keywords: 壁関数,Wall function,kqRWallFunction,epsilonWallFunction,nutkWallFunction,yPlusLam
壁面境界条件
k‐εモデルにおける壁面境界条件の設定の仕方は次の2つである
- 標準k‐εモデルを使って第1格子点を対数領域(\(30 \leq y^{+} \leq 200\))に配置し,壁面の境界条件として壁関数とよばれる関数を設定する
- 低レイノルズ数型k‐εモデルを使って第1格子点を粘性低層(\(y^{+} \leq 2 \sim 4\))に配置し,壁面の境界条件として滑りなし条件を設定する
速度と圧力についてはどちらのモデルも共通で \(u_{i}=0\),\(\frac{\partial p}{\partial n}=0\) を設定する
対数領域(壁関数)の添え字を\(_{log}\),粘性低層(すべりなし条件)の添え字を\(_{vis}\)とすると,乱流エネルギー,乱流散逸率,渦粘性係数の壁面境界条件は次のようになる
(乱流エネルギー)
\begin{align}
&\frac{\partial k_{log}}{\partial y}=0 \\
\\
&k_{vis}=0
\end{align}
(乱流散逸率)
\begin{align}
&\varepsilon_{log}=\frac{C_{\mu}^{\frac{3}{4}}k^{\frac{3}{2}}}{\kappa y} \\
\\
&\varepsilon_{vis}=\frac{2\nu k}{y^2}
\end{align}
(渦粘性係数)
\begin{align}
&\nu_{t_{log}}=\nu\left(\frac{\kappa y^{+}}{\mathrm{ln}\left(Ey^{+}\right)}-1\right) \\
\\
&\nu_{t_{vis}}=0
\end{align}
ここで,\(y^{+}\)は摩擦速度\(u_{\tau}\)によって無次元化された壁面からの距離である
\begin{align}
y^{+}=\frac{C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}y}{\nu}
\end{align}
壁面上の\(\nu_{t}\)の値は\(k\)と\(\varepsilon\)の壁関数を与えた時点で計算できるが,CFDでは数値計算の都合上\(\nu_{t}\)にも壁関数を適用する
壁関数の導出についてはこちら
すべりなし条件の導出についてはこちら
それぞれの条件について説明していく
kqRWallFunction
参考
≫OpenFOAM User Guide kqRWallFunction
≫kqRWallFunctionFvPatchField.C
≫OpenFOAM User Guide Fixed value
乱流エネルギー\(k\)の壁関数にはkqRWallFunctionを使い,すべりなし条件にはfixedValueを使う
\begin{align}
&\frac{\partial k_{log}}{\partial y}=0
\end{align}
template<class Type>
void Foam::kqRWallFunctionFvPatchField<Type>::evaluate
(
const Pstream::commsTypes commsType
)
{
zeroGradientFvPatchField<Type>::evaluate(commsType);
}\begin{align}
k_{vis}=0
\end{align}
<patchName>
{
type fixedValue;
value 0;
}epsilonWallFunction
参考
≫OpenFOAM User Guide epsilonWallFunction
≫epsilonWallFunctionFvPatchScalarField.C
乱流散逸率\(\varepsilon\)の壁面境界条件にはepsilonWallFunctionを使う
\begin{align}
&\varepsilon_{log}=\frac{C_{\mu}^{\frac{3}{4}}k^{\frac{3}{2}}}{\kappa y} \\
\\
&\varepsilon_{vis}=\frac{2\nu k}{y^2}
\end{align}
\(w\)は角付近の壁関数を計算するための係数である
const scalar w = cornerWeights[facei];
scalar epsilonBlended = 0.0;
// Contribution from the viscous sublayer
const scalar epsilonVis = w*2.0*k[celli]*nuw[facei]/sqr(y[facei]);
// Contribution from the inertial sublayer
const scalar epsilonLog =
w*Cmu75*pow(k[celli], 1.5)/(nutw.kappa()*y[facei]);\(\varepsilon_{vis}\)と\(\varepsilon_{log}\)の切り替えは4つの方法から選択する
(stepwise switch)
\begin{equation}
\varepsilon=\left\{\begin{array}{ll}
\varepsilon_{vis} & \left(y^{+}<y_{lam}^{+}\right) \\
\varepsilon_{log} & \left(y^{+}>y_{lam}^{+}\right)
\end{array}\right.
\end{equation}
(maximum-value switch)
\begin{equation}
\varepsilon=\mathrm{max}\left[\varepsilon_{vis},\;\varepsilon_{log}\right]
\end{equation}
(binomial blending)
\begin{equation}
\varepsilon=\left(\varepsilon_{vis}^{n}+\varepsilon_{log}^{n}\right)^{\frac{1}{n}}
\end{equation}
(stepwise switch)
\begin{equation}
\varepsilon=\varepsilon_{vis}\exp{\left(-\Gamma\right)}+\varepsilon_{log}\exp{\left(-\frac{1}{\Gamma}\right)} \\
\Gamma=\frac{0.001{y^{+}}^{4}}{1.0+y^{+}}
\end{equation}
switch (blending_)
{
case blendingType::STEPWISE:
{
if (lowReCorrection_ && yPlus < nutw.yPlusLam())
{
epsilonBlended = epsilonVis;
}
else
{
epsilonBlended = epsilonLog;
}
break;
}
case blendingType::MAX:
{
// (PH:Eq. 27)
epsilonBlended = max(epsilonVis, epsilonLog);
break;
}
case blendingType::BINOMIAL:
{
// (ME:Eqs. 15-16)
epsilonBlended =
pow
(
pow(epsilonVis, n_) + pow(epsilonLog, n_),
1.0/n_
);
break;
}
case blendingType::EXPONENTIAL:
{
// (PH:p. 193)
const scalar Gamma = 0.001*pow4(yPlus)/(1.0 + yPlus);
const scalar invGamma = 1.0/(Gamma + ROOTVSMALL);
epsilonBlended =
epsilonVis*exp(-Gamma) + epsilonLog*exp(-invGamma);
break;
}
}nutkWallFunctionFvPatchScalarField
参考
≫OpenFOAM User Guide nutkWallFunction
≫nutkWallFunctionFvPatchScalarField.C
渦粘性係数\(\nu_{t}\)の壁面境界条件にはnutkWallFunctionFvPatchScalarFieldを使う
\begin{align}
&\nu_{t_{log}}=\nu\left(\frac{\kappa y^{+}}{\mathrm{ln}\left(Ey^{+}\right)}-1\right) \\
\\
&\nu_{t_{vis}}=0
\end{align}
forAll(nutw, facei)
{
const label celli = patch().faceCells()[facei];
const scalar yPlus = Cmu25*y[facei]*sqrt(k[celli])/nuw[facei];
// Viscous sublayer contribution
const scalar nutVis = 0.0;
// Inertial sublayer contribution
const scalar nutLog =
nuw[facei]*(yPlus*kappa_/log(max(E_*yPlus, 1 + 1e-4)) - 1.0);
nutw[facei] = blend(nutVis, nutLog, yPlus);
} \(\nu_{t_{vis}}\)と\(\nu_{t_{log}}\)の切り替えは4つの方法から選択するが,それらは親クラスである nutWallFunctionFvPatchScalarFieldで定義されている
≫OpenFOAM User Guide nutWallFunction
≫nutWallFunctionFvPatchScalarField.C
(stepwise switch)
\begin{equation}
\nu_{t}=\left\{\begin{array}{ll}
\nu_{t_{vis}} & \left(y^{+}<y_{lam}^{+}\right) \\
\nu_{t_{log}} & \left(y^{+}>y_{lam}^{+}\right)
\end{array}\right.
\end{equation}
(maximum-value switch)
\begin{equation}
\nu_{t}=\mathrm{max}\left[\nu_{t_{vis}},\;\nu_{t_{log}}\right]
\end{equation}
(binomial blending)
\begin{equation}
\nu_{t}=\left(\nu_{t_{vis}}^{n}+\nu_{t_{log}}^{n}\right)^{\frac{1}{n}}
\end{equation}
(stepwise switch)
\begin{equation}
\nu_{t}=\nu_{t_{vis}}\exp{\left(-\Gamma\right)}+\nu_{t_{log}}\exp{\left(-\frac{1}{\Gamma}\right)} \\
\Gamma=\frac{0.01{y^{+}}^{4}}{1.0+5.0y^{+}}
\end{equation}
Foam::scalar Foam::nutWallFunctionFvPatchScalarField::blend
(
const scalar nutVis,
const scalar nutLog,
const scalar yPlus
) const
{
scalar nutw = 0.0;
switch (blending_)
{
case blendingType::STEPWISE:
{
if (yPlus > yPlusLam_)
{
nutw = nutLog;
}
else
{
nutw = nutVis;
}
break;
}
case blendingType::MAX:
{
// (PH:Eq. 27)
nutw = max(nutVis, nutLog);
break;
}
case blendingType::BINOMIAL:
{
// (ME:Eqs. 15-16)
nutw =
pow
(
pow(nutVis, n_) + pow(nutLog, n_),
1.0/n_
);
break;
}
case blendingType::EXPONENTIAL:
{
// (PH:Eq. 31)
const scalar Gamma = 0.01*pow4(yPlus)/(1.0 + 5.0*yPlus);
const scalar invGamma = 1.0/(Gamma + ROOTVSMALL);
nutw = nutVis*exp(-Gamma) + nutLog*exp(-invGamma);
break;
}
}
return nutw;
}yPlusLam
stepwise switch の条件分岐に出てきている\(y^{+}_{lam}\)は,粘性定数の速度分布\(u_{\tau}=y^{+}\)と対数領域の速度分布\(u_{\tau}=\frac{1}{\kappa}\ln{Ey^{+}}\)の好天における\(y^{+}\)である
\begin{equation}
y^{+}_{lam}=\frac{\ln{Ey^{+}_{lam}}}{\kappa}
\end{equation}
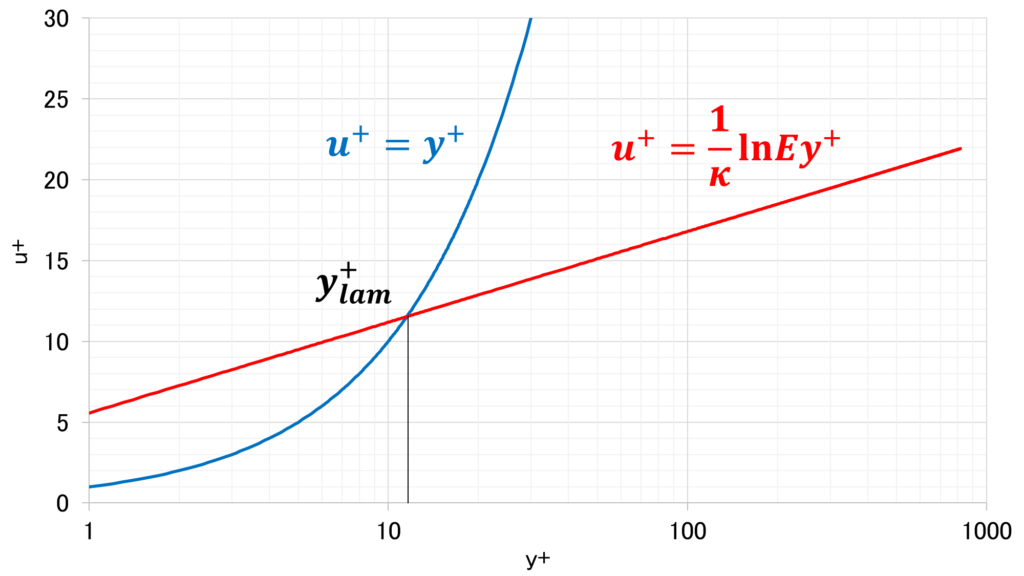
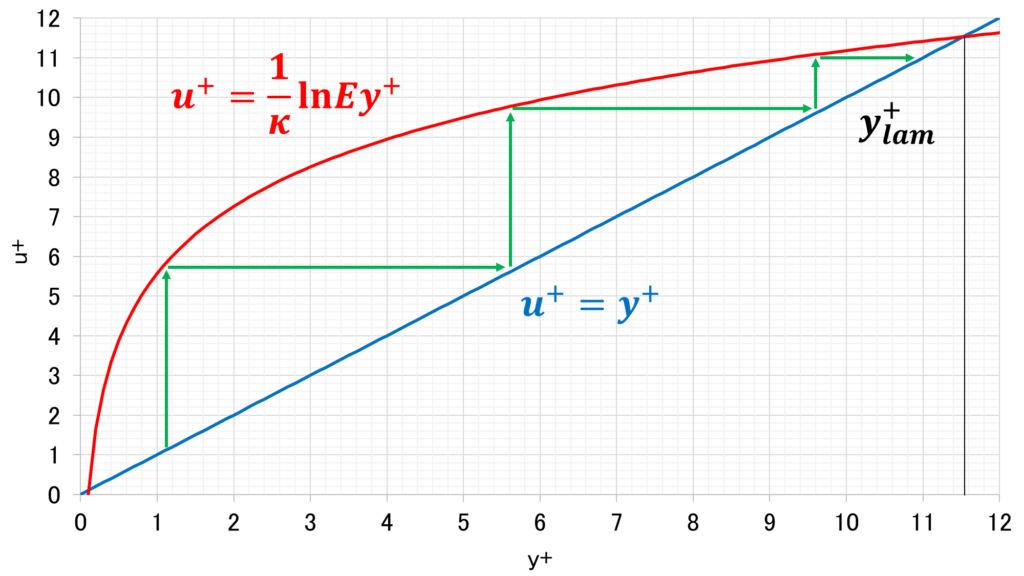
\(y^{+}_{lam}\)はnutWallFunctionFvPatchScalarFieldにおいてニュートン法の反復計算によって求められている
Foam::scalar Foam::nutWallFunctionFvPatchScalarField::yPlusLam
(
const scalar kappa,
const scalar E
)
{
scalar ypl = 11.0;
for (label i = 0; i < 10; ++i)
{
ypl = log(max(E*ypl, 1.0))/kappa;
}
return ypl;
}イメージはこんな感じ
まとめ
OpenFOAMで実装されているk‐εモデルの壁関数について説明した
乱流エネルギー\(k\)の壁関数にはkqRWallFunctionを使い,すべりなし条件にはfixedValueを使う
乱流散逸率\(\varepsilon\)の壁面境界条件にはepsilonWallFunctionを使う
渦粘性係数\(\nu_{t}\)の壁面境界条件にはnutkWallFunctionFvPatchScalarFieldを使う
\(\varepsilon\)と\(\nu_{t}\)では,\(_{log}\)と\(_{vis}\)のブレンドの方法を4つの中から選択する必要がある
そのほかの乱流モデルについてはこちら





コメント