離散化されたデータを最小二乗法を用いて多変数関数の多項式近似を行うExcelマクロについて説明する
↓Excel関数でやりたい人はこちら
最小二乗法の定式化 (Least Square Method)
最小二乗法を用いた多変数関数の多項式近似とは,離散化されたデータに対して最もいい感じにフィットするような多項式の係数を計算する方法である
最小二乗法の行列表現:
最小二乗法の行列表現(単回帰,多変数,多項式)
主張1: 行列\({\bf A}\)と列ベクトル\({\bf b}\)が与えられたときに
\(||{\bf Ax-b}||\)
を最小にする\({\bf x}\)を求める問題は非常に重要である。
主張2:\({\bf A^t A}\)が正則のとき上記の問題の解は唯一つである:
\({\bf x=(A^T A)^{-1} A^T b}\)
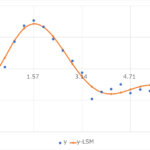
今回の例だとこんな感じになる
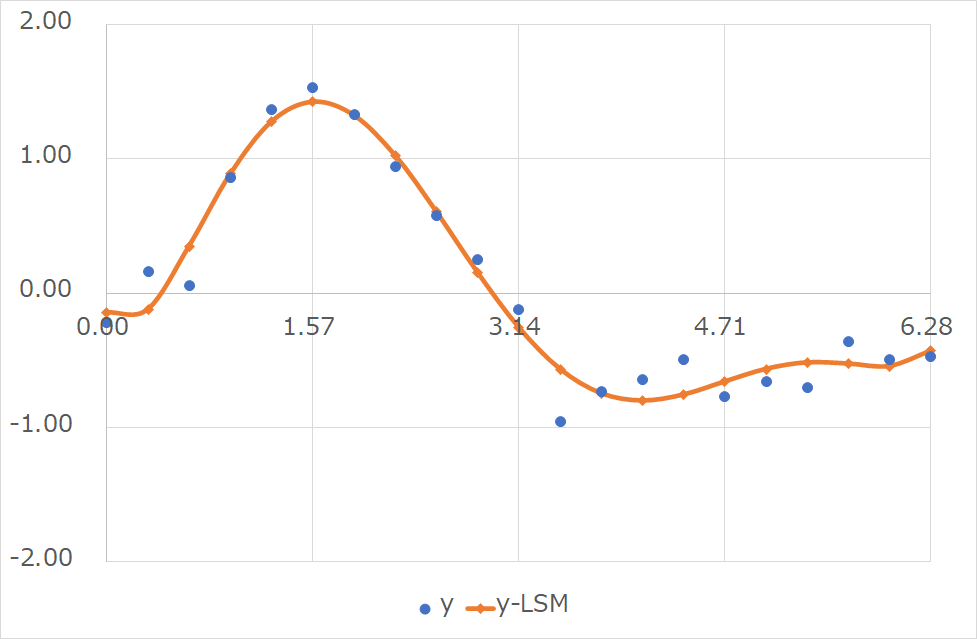
ここでは,適当に生成した乱数波\(y(x)\)の離散データに対して,6次多項式で近似を行った
\begin{align}
y_{_{LSM}}&=\sum_{i=0}^{6}\left(a_{i}x^{i}\right)\\
&=a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}+a_{6}x^{6}
\end{align}
離散データとしては大量の\(x_{0},~x_{1},~\cdots,~x_{6},~y\)の組が与えられる
\(x_{0},~x_{1},~\cdots,~x_{6}\)の組を\({\bf A}\),\(y\)の組を\({\bf b}\),これらにベストフィットする係数\(a_{0},~a_{1},\cdots,~a_{6}\)の組を\({\bf x}\)として, \({\bf x=(A^T A)^{-1} A^T b}\)を計算する
Excelで最小二乗法の解を求める
↓Excelファイルのダウンロードはこちら
Least-Square-Method-Macro.xlsm
シートの構成はこんな感じ
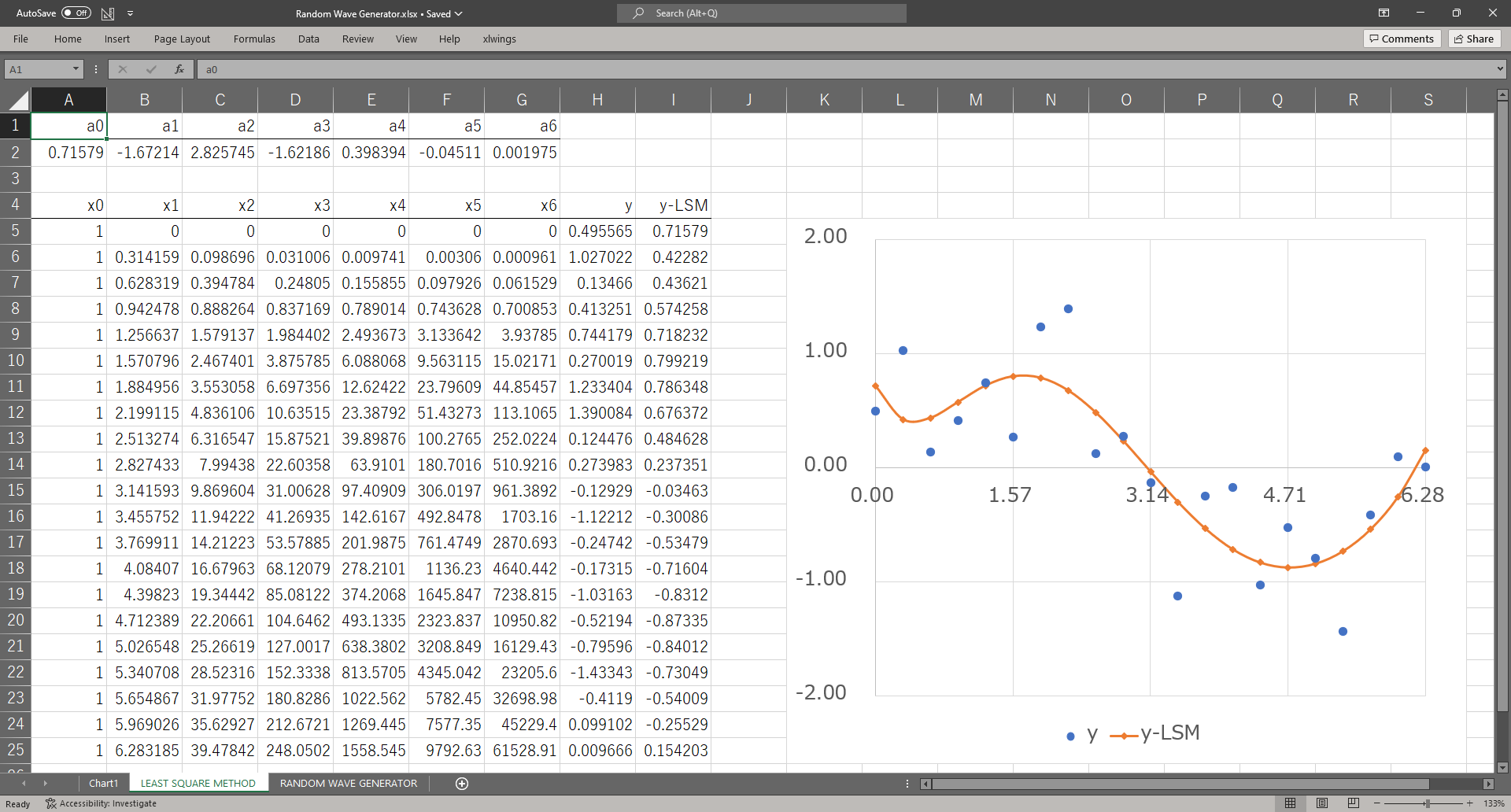
A列からH列の5行目から25行目までに\(x_{0},~x_{1},~\cdots,~x_{6}\)とそれに対応する\(y\)の組が入力されている
(\(x_0\)は定数項なので1が入力されている)
ソースコードはこれ
Sub LeastSquareMethod()
'参考文献:https://mathtrain.jp/leastsquarematrix
'変数の宣言
Dim data1 As Integer: data1 = 21
Dim data2 As Integer: data2 = 7
Dim matrix1() As Double 'A
Dim matrix2() As Double 'At
Dim matrix3() As Double '(At A)
Dim matrix4() As Double '(At A)^-1
Dim matrix5() As Double '(At A)^-1 At
Dim matrix6() As Double 'b
Dim matrix7() As Double '(At A)^-1 At b
Dim output(0, 100) As Double '係数出力用の配列
'カウンター
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim n As Integer
'タイマーの変数
Dim startTime As Double
Dim endTime As Double
Dim processTime As Double
'ActiveWorkbook.Save'まず上書き保存
Application.ScreenUpdating = False '画面更新の非表示
Application.DisplayAlerts = False '警告画面の非表示
startTime = Timer '開始時間取得
ReDim matrix1(data1 - 1, data2 - 1)
ReDim matrix6(data1 - 1, 0)
'多変数関数の配列の作成
For i = 0 To data1 - 1
For j = 0 To data2 - 1
matrix1(i, j) = Cells(5 + i, 1 + j) 'x_i
Next j
matrix6(i, 0) = Cells(5 + i, 8) 'y
Next i
matrix2 = Transpose(data1, data2, matrix1) 'At
matrix3 = mult(matrix2, matrix1) '(At・A)
matrix4 = inverse(data2, matrix3) '(At A)^-1
matrix5 = mult(matrix4, matrix2) '(At A)^-1 At
matrix7 = mult(matrix5, matrix6) '(At A)^-1 At b
For i = 0 To data2 - 1
output(0, i) = matrix7(i, 0)
Next i
Range(Cells(2, 1), Cells(2, data2)) = output()
'終了時間取得
endTime = Timer
'処理時間表示
processTime = endTime - startTime
MsgBox "計算が終了しました" & vbCrLf & "処理時間:" & processTime
End SubPublic Function ans(ByVal n As Integer, ByRef A() As Double, ByRef b() As Double) As Double()
'ガウスの消去法によって,連立方程式Ax=bを解く.
'Aはn×n行列,x,bはn×1行列
'参考文献:「解析塾秘伝!有限要素法のつくり方」 p.82-
'変数の宣言
Dim pivot As Double 'マトリックスの体格成分
Dim p As Double '計算に使用するマトリックスの成分
Dim x() As Double '解を入れる配列
ReDim x(n - 1)
'カウンター
Dim r As Integer
Dim c As Integer
Dim rr As Integer
Dim cc As Integer
'画面更新の非表示
Application.ScreenUpdating = False
'前進消去
For r = 0 To n - 1
pivot = A(r, r) '対角成分をpivotに代入
For c = r To n - 1
A(r, c) = A(r, c) / pivot
Next c
b(r) = b(r) / pivot
For rr = r + 1 To n - 1
p = A(rr, r)
For cc = r To n - 1
A(rr, cc) = A(rr, cc) - p * A(r, cc)
Next cc
b(rr) = b(rr) - p * b(r)
Next rr
Next r
'後退代入
For r = n - 1 To 0 Step -1
x(r) = b(r)
For c = r + 1 To n - 1
x(r) = x(r) - A(r, c) * x(c)
Next c
Next r
ans = x
End FunctionPublic Function inverse(ByVal n As Integer, ByRef b() As Double) As Double()
'掃き出し法により逆行列を計算する
'参考資料:http://www.econ.nagoya-cu.ac.jp/~kamiyama/siryou/minv.html
Dim nn As Integer
Dim p As Double 'ピボット
Dim c As Double '行
Dim x As Double
Dim y As Double
Dim A() As Double
Dim Binv() As Double
nn = n + n
ReDim A(n - 1, nn - 1)
ReDim Binv(n - 1, n - 1)
'左半分に逆行列を求めたい行列を入れる
For i = 0 To n - 1
For j = 0 To n - 1
A(i, j) = b(i, j)
Next j
Next i
'行列の右半分に単位行列を入れる
For i = 0 To n - 1
For j = n To nn - 1
A(i, j) = 0
Next j
A(i, i + n) = 1
Next i
'掃き出し法の基本操作
For k = 0 To n - 1
p = 0: c = 0
'k行以降で絶対値が最も大きい行を調べる
For i = k To n - 1
If Abs(A(i, k)) > p Then
p = Abs(A(i, k))
c = i
End If
Next i
'k行目とc行目の成分を入れ替える
If c <> k Then
For j = k To nn - 1
y = A(k, j)
A(k, j) = A(c, j)
A(c, j) = y
Next j
End If
'k行目以降の対角成分をk行目の対角成分で割る
x = A(k, k)
For j = k To nn - 1
A(k, j) = A(k, j) / x
Next j
For i = 0 To n - 1
If i <> k Then
x = A(i, k)
For j = k To nn - 1
A(i, j) = A(i, j) - x * A(k, j)
Next j
End If
Next i
Next k
For i = 0 To n - 1
For j = n To nn - 1
Binv(i, j - n) = A(i, j)
Next j
Next i
inverse = Binv
End FunctionPublic Function mult(m1() As Double, m2() As Double) As Double()
'm1[l,m]*m2[m,n]の行列の掛け算を行う
Dim l As Integer
Dim m As Integer
Dim n As Integer
Dim sum As Double
Dim ans() As Double
'カウンター
Dim i As Integer
Dim j As Integer
Dim k As Integer
'行列の大きさを取得
l = UBound(m1, 1)
m = UBound(m1, 2)
n = UBound(m2, 2)
'配列の大きさを定義
ReDim ans(l, n)
For i = 0 To l
For j = 0 To n
sum = 0
For k = 0 To m
sum = sum + m1(i, k) * m2(k, j)
Next k
ans(i, j) = sum
Next j
Next i
mult = ans
End FunctionPublic Function Transpose(ByVal m As Integer, ByVal n As Integer, ByRef A() As Double) As Double()
'転置行列を計算する
'Aはm×n行列,Atはn×m行列
'変数の宣言
Dim At() As Double '解を入れる配列
ReDim At(n - 1, m - 1) '解を入れる配列
'カウンター
Dim r As Integer
Dim c As Integer
For r = 0 To m - 1
For c = 0 To n - 1
At(c, r) = A(r, c)
Next c
Next r
Transpose = At
End Functionまとめ
離散化されたデータを最小二乗法を用いて多項式近似するExcelマクロについて説明した
今回はn次多項式で説明したが、¥(x_{i}¥)についてはlogでもsinでもexpでもなんでもいい
↓関連記事


コメント