離散化されたデータを最小二乗法を用いて多変数関数の多項式近似を行う方法について説明する
↓Excel VBAでやりたい人はこちら
最小二乗法の定式化 (Least Square Method)
最小二乗法を用いた多変数関数の多項式近似とは,離散化されたデータに対して最もいい感じにフィットするような多項式の係数を計算する方法である
最小二乗法の行列表現:
最小二乗法の行列表現(単回帰,多変数,多項式)
主張1: 行列\({\bf A}\)と列ベクトル\({\bf b}\)が与えられたときに
\(||{\bf Ax-b}||\)
を最小にする\({\bf x}\)を求める問題は非常に重要である。
主張2:\({\bf A^t A}\)が正則のとき上記の問題の解は唯一つである:
\({\bf x=(A^T A)^{-1} A^T b}\)
今回の例だとこんな感じになる
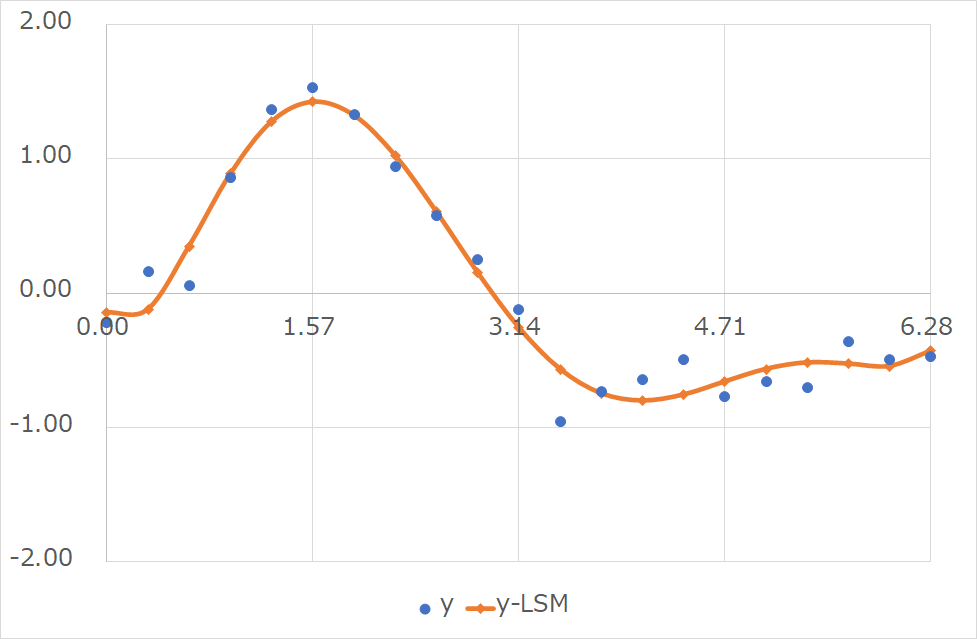
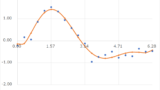
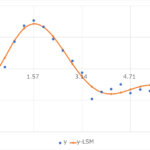
ここでは,適当に生成した乱数波\(y(x)\)の離散データに対して,6次多項式で近似を行った
\begin{align}
y_{_{LSM}}&=\sum_{i=0}^{6}\left(a_{i}x^{i}\right)\\
&=a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}+a_{6}x^{6}
\end{align}
離散データとしては大量の\(x_{0},~x_{1},~\cdots,~x_{6},~y\)の組が与えられる
\(x_{0},~x_{1},~\cdots,~x_{6}\)の組を\({\bf A}\),\(y\)の組を\({\bf b}\),これらにベストフィットする係数\(a_{0},~a_{1},\cdots,~a_{6}\)の組を\({\bf x}\)として, \({\bf x=(A^T A)^{-1} A^T b}\)を計算する
Excelで最小二乗法の解を求める
↓Excelファイルのダウンロードはこちら
シートの構成はこんな感じ
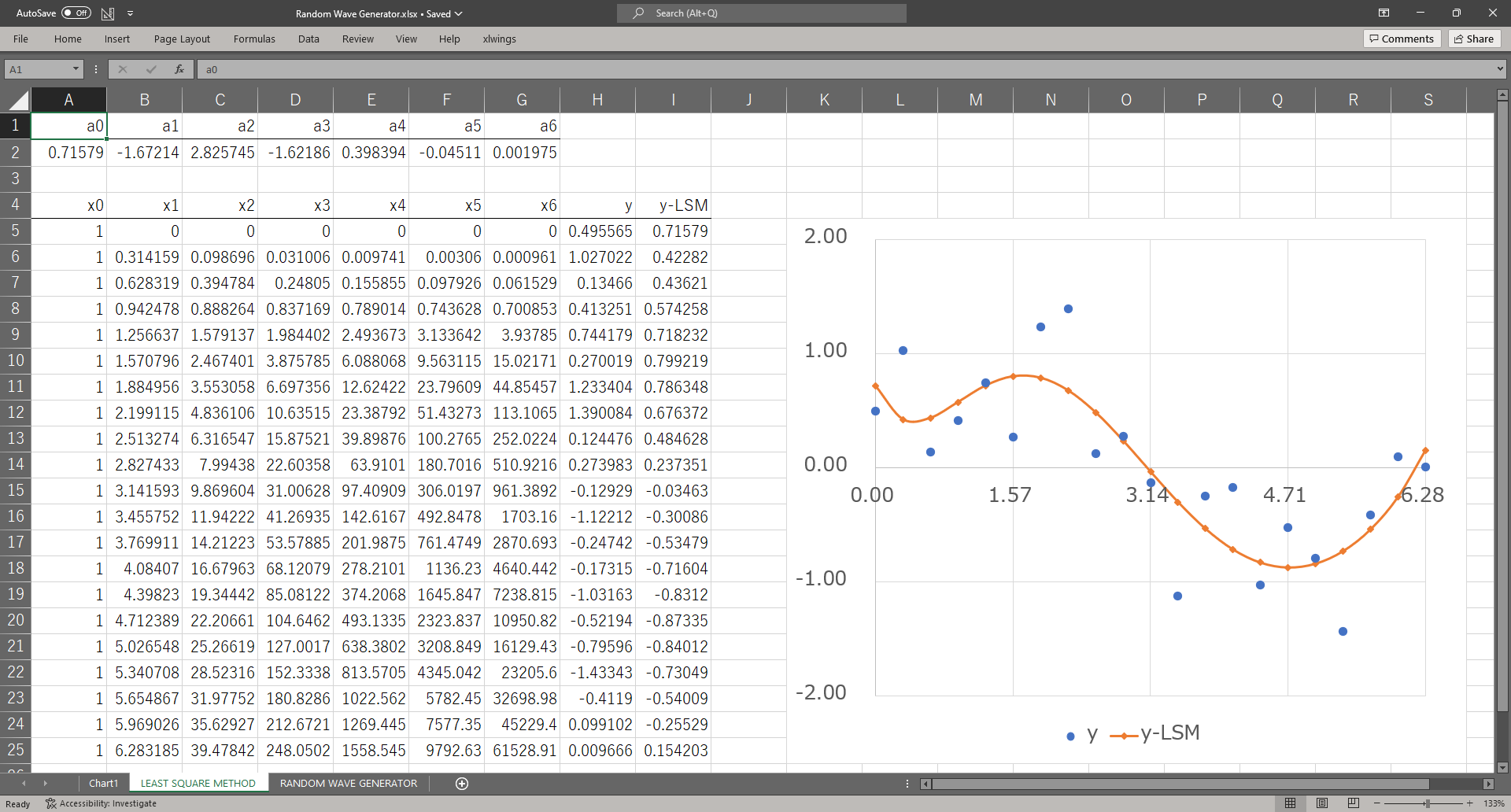
A列からH列の5行目から25行目までに\(x_{0},~x_{1},~\cdots,~x_{6}\)とそれに対応する\(y\)の組が入力されている
(\(x_0\)は定数項なので1が入力されている)
最小二乗法の解を求めるためには、セルA1からセルG1を選択した状態でF2キーを押して以下の数式を入力し,「Ctrl+Shift+Enter」で確定する
\begin{equation}
{\bf x=(A^T A)^{-1} A^T b}
\end{equation}
=TRANSPOSE(MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A5:G25),A5:G25)),TRANSPOSE(A5:G25)),H5:H25))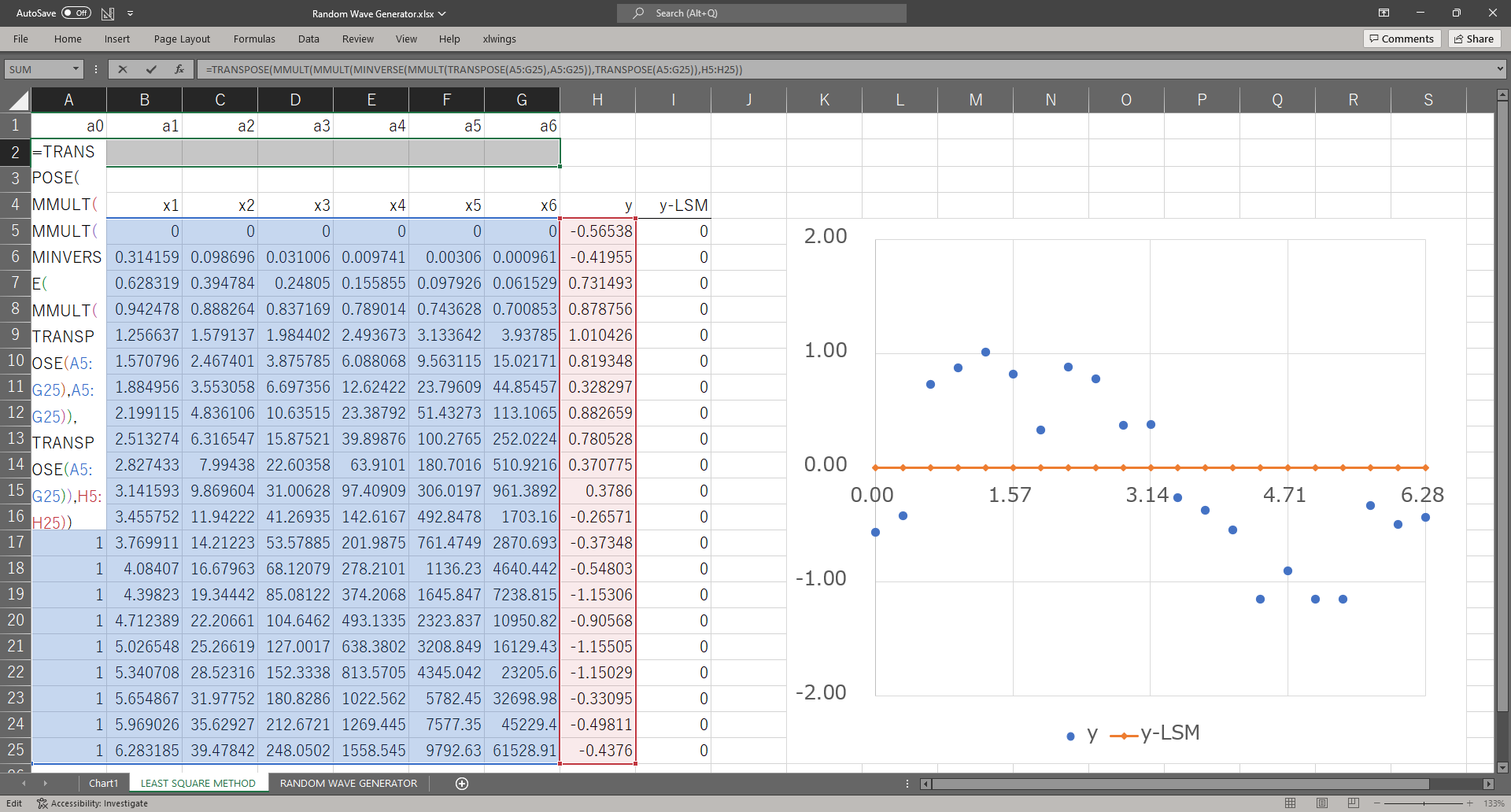
MMULT関数、MINVERSE関数、TRANSPOSE関数はそれぞれ行列の積、逆行列、転置行列を計算する関数である
\(y_{_LSM}\)は最小二乗法で求めた係数と\(x_{0},~x_{2},~\cdots,~x_{6}\)をSUMPRODUCT関数にいれれば計算できる
=SUMPRODUCT($A$2:$G$2,A5:G5)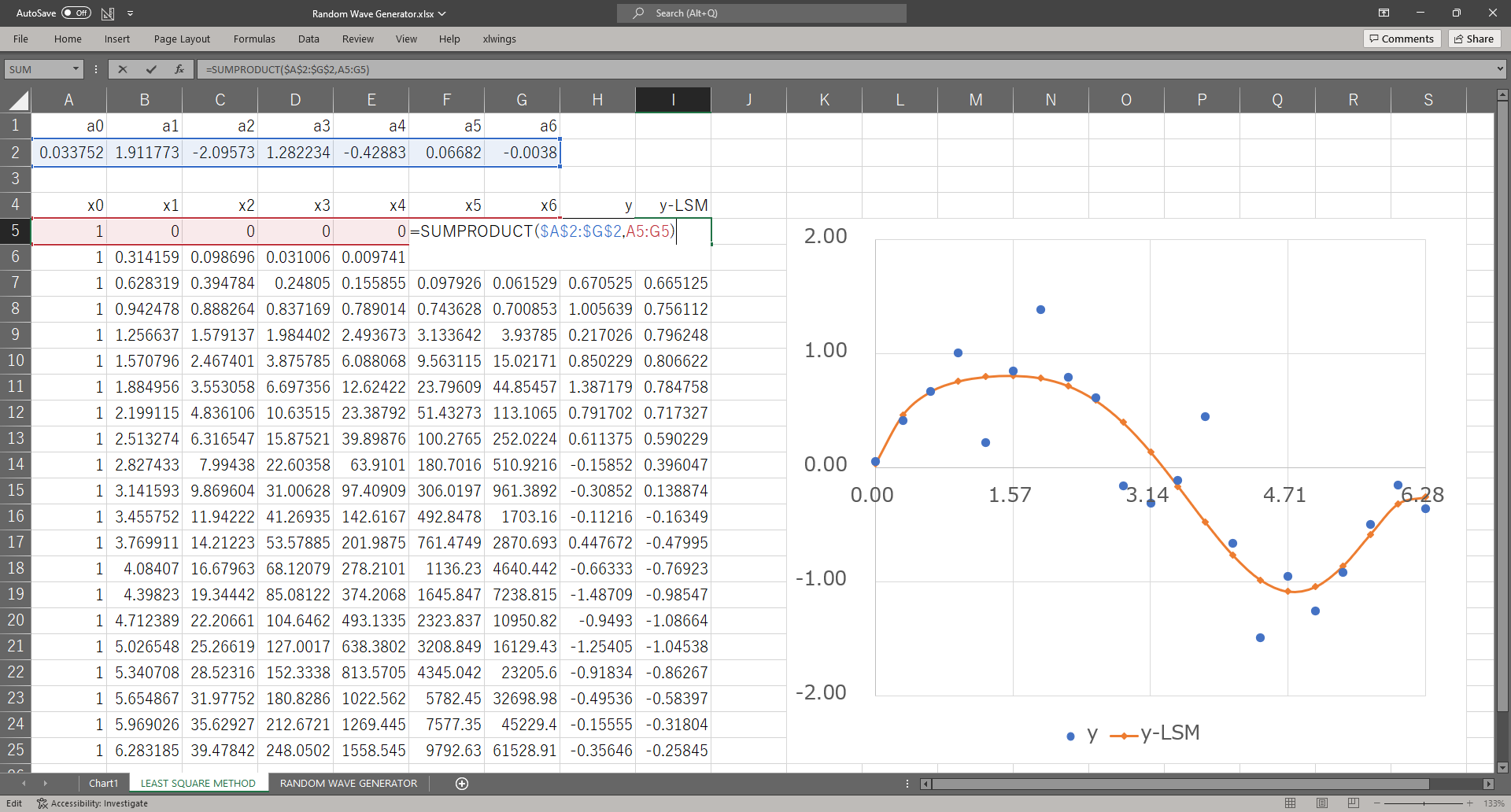
まとめ
離散化されたデータを最小二乗法を用いて多項式近似する方法について説明した
今回はn次多項式で説明したが、¥(x_{i}¥)についてはlogでもsinでもexpでもなんでもいい
↓関連記事


コメント