最大応力説で破断合力を計算する

最大応力説を使って積層板の破断合力を計算する

目的とフローチャート
プログラムの解説
プログラムの実行
まとめ

目的とフローチャート

今回の目的は，最大応力説を使って積層板の破断合力を計算することである

基本的には前回の記事の内容をExcel VBAで書き直すだけなので，詳しくは前回の記事を参考にしてほしい

数学の分野ではよく「エレガントな解法」という言葉があるが，それとは逆にプログラミングを使った力任せな解き方を「エレファントな解法」というらしい

今回のプログラミングはまさにこの「エレファントな解法」である

（たぶん）積層板の破断合力は解析的に計算することはできないので，それっぽい値を代入して毎回破断するかどうか判断していくしかない

今回のプログラムでは，例えば破断合力が\( N_x\) =1'234'567[N/m]だとすると，まず1’000’000[N/m]から1'000'000[N/m]刻みで計算して2'000'000[N/m]で破断，1'000'000[N/m]に戻って100'000[N/m]刻みで計算して1'300'000[N/m]で破断，1'200'000[N/m]に戻って10'000[N/m]刻みで計算して1'240'000[N/m]で破断，・・・という計算を繰り返していくことになる

フローチャートを以下に示す

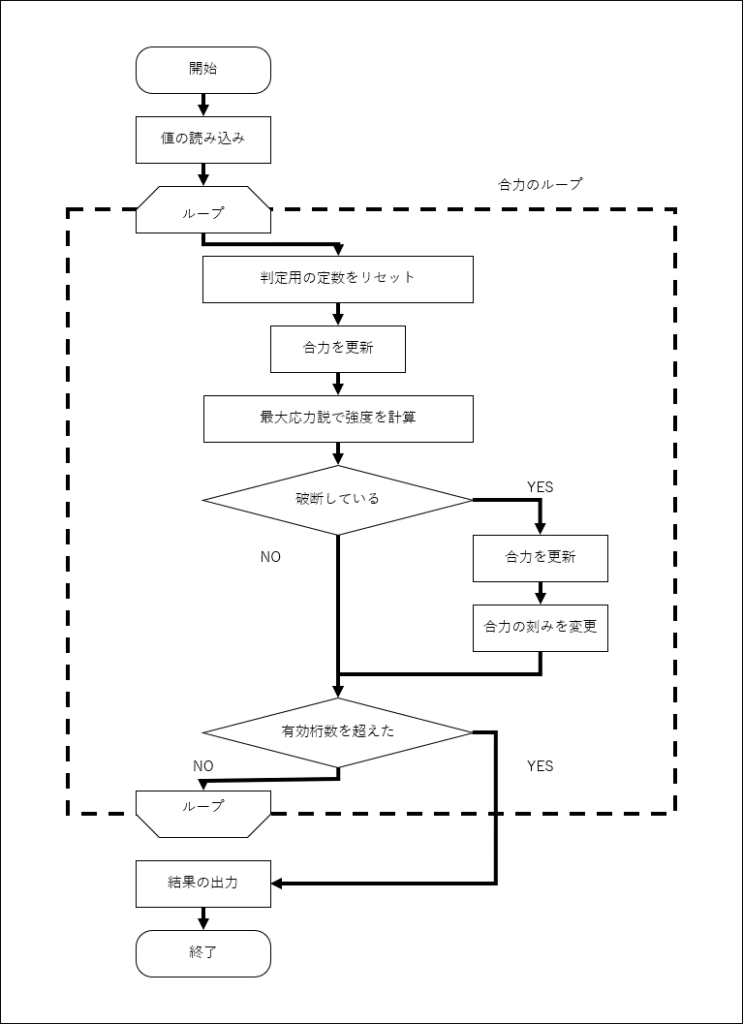
合力のループについては，無限ループに近いものを回して，「与えられた有効桁数を超える」という条件を満たせばループを抜けるようにする

テンプレートファイルのダウンロード

エクセルの数式などの参考になるようにテンプレートファイルを添付しておく

最大応力説

1 ファイル 21.56 KB

ダウンロード

プログラムの解説

それでは実際に解説していく

使用する変数

マクロに使用する変数を以下に示す

'変数の宣言
Dim sf As Integer '有効桁数
Dim dN As Double '合応力の増分 [N/m]
Dim fracture As Integer '破断したかどうかの判定に使う．0なら破断していない．
Dim ply As Integer '積層数 [ply]
Dim Qxy() As Double 'プリプレグ1枚のxy方向の剛性行列 [GPa]
Dim FLt As Double '繊維方向引張強度 [GPa]
Dim FLc As Double '繊維方向圧縮強度 [GPa]
Dim FTt As Double '直交方向引張強度 [GPa]
Dim FTc As Double '直交方向圧縮強度 [GPa]
Dim FLTs As Double 'せん断強度 [GPa]
Dim z() As Double '中心からの距離 [m]
Dim theta() As Double '積層角 [rad]
Dim Kinv(5, 5) As Double '剛性行列の逆行列
Dim strain0() As Double '積層板としてのひずみ
Dim strain() As Double 'プリプレグごとのひずみ
Dim stress0(5, 0) As Double '積層板としての合応力，合モーメント
Dim stress() As Double '層ごとの応力 [GPa]
Dim stressLT() As Double '層ごとの繊維方向の応力 [GPa]
'カウンター
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim l As Integer
'その他
Dim num As Integer '有効桁数のカウンター
Dim tmp() As Double

変数が増えて楽しくなってきた

変数の意味については，前回(≫最大応力説で積層板の強度を計算する）や，前々回（≫古典積層理論）を確認してほしい

積層板の剛性行列などをいちいち計算するのは面倒なので，シートで計算した剛性行列の逆行列と各層の\( \overline{\bf Q} \)のみを読み込む

値の読み込み

エクセルシートから必要な値を読み込む

新しく入力する変数は合力の有効桁数sfのみである

'合応力の増分の初期値を設定
dN = -1000000

'値の読み込み
sf = Range("D35") '有効桁数
ply = Range("I29") '積層数
FLt = Range("D4") '繊維方向引張強度 [GPa]
FLc = Range("D10") '繊維方向圧縮強度 [GPa]
FTt = Range("D7") '直交方向引張強度 [GPa]
FTc = Range("D13") '直交方向圧縮強度 [GPa]
FLTs = Range("D16") 'せん断強度 [GPa]
For i = 0 To 5
    For j = 0 To 5
        Kinv(i, j) = Cells(11 + i, 12 + j) '剛性行列の逆行列
    Next j
Next i

'配列の定義
ReDim theta(ply - 1)
ReDim z(ply - 1)
ReDim Qxy(2, 2, ply - 1)
ReDim strain(2, 0) 'プリプレグごとのひずみ
ReDim stress(2, 0) '層ごとの応力 [GPa]
ReDim stressLT(2, 0) '層ごとの繊維方向の応力 [GPa]

'値の読み込み
For i = 0 To ply - 1
    theta(i) = Cells(5, 24 + i) '積層角 [rad]
    z(i) = (Cells(6, 24 + i) + Cells(7, 24 + i)) / 2 '中心からの距離 [m]
    'Qxyの読み込み
    Qxy(0, 0, i) = Cells(11, 24 + i)
    Qxy(0, 1, i) = Cells(12, 24 + i)
    Qxy(1, 1, i) = Cells(13, 24 + i)
    Qxy(0, 2, i) = Cells(14, 24 + i)
    Qxy(1, 2, i) = Cells(15, 24 + i)
    Qxy(2, 2, i) = Cells(16, 24 + i)
    Qxy(1, 0, i) = Qxy(0, 1, i)
    Qxy(2, 0, i) = Qxy(0, 2, i)
    Qxy(2, 1, i) = Qxy(1, 2, i)
Next i

合力の増分の初期値はそれっぽい値を入力しておく

いくつかの配列の大きさは積層数によって変化するので，まず積層数を読み込んでから動的配列の大きさを宣言し，そのあとで必要な値を読み込む必要がある

合力のループ

合力のループは，なんちゃって無限ループにしておく

'破断する合力を求めるループ
num = 0 '有効桁数のカウンター
For i = 0 To 1000
      （合力のループの中の処理）
Next i

ループに入る前に有効桁数のカウンターを初期化しておく

判定用の定数をリセット

ループの最初で，破断したかどうかの判定用の定数fractureをリセットしておく

fracture = 0 '破断したかどうかの判定に使う．0なら破断していない．

このあと，層ごとに破断しているかどうか判定するループの中で，層が破断していれば判定用の定数fractureに1を足していく

ループの最後でfractureが0でなければどこかの層が破断していたと判断することができる

合力の更新

合力の値を更新する

'積層板全体にはたらく合力を計算
stress0(0, 0) = stress0(0, 0) + dN 'Nxに初期値を代入 [N/m]

x方向の破断合力以外を求めたいならここを書き換えればいい

ループの1周目ではdNには上で入力した初期値が入っており，どこかの層が破断するたびにdNは0.1倍されていく

最大応力説で強度を計算する

ただただ前回(≫最大応力説で積層板の強度を計算する)の内容をExcel VBAで書き直すだけ

 '積層板全体のひずみを計算[-]
strain0 = mult(Kinv, stress0)
For j = 0 To ply - 1 '層ごとのループ
    'Qxyの計算 [GPa]
    ReDim tmp(2, 2)
    For l = 0 To 2
        For k = 0 To 2
            tmp(k, l) = Qxy(k, l, j)
        Next k
    Next l
    '積層板全体のひずみから層ごとのひずみを計算
    For k = 0 To 2 'ひずみ成分ごとのループ [-]
        strain(k, 0) = strain0(k, 0) + strain0(3 + k, 0) * z(j)
    Next k
    '層ごとの応力の計算 [GPa]
    stress = mult(tmp, strain)
    '層ごとの応力を主軸方向に変換 [GPa]
    stressLT(0, 0) = (stress(0, 0) + stress(1, 0)) / 2 + (stress(0, 0) - stress(1, 0)) / 2 * Cos(2 * theta(j)) + stress(2, 0) * Sin(2 * theta(j))
    stressLT(1, 0) = (stress(0, 0) + stress(1, 0)) / 2 - (stress(0, 0) - stress(1, 0)) / 2 * Cos(2 * theta(j)) - stress(2, 0) * Sin(2 * theta(j))
    stressLT(2, 0) = -((stress(0, 0) - stress(1, 0)) / 2) * Sin(2 * theta(j)) + stress(2, 0) * Cos(2 * theta(j))
    '破断しているかどうかの判定
    If FLc < stressLT(0, 0) And stressLT(0, 0) < FLt And FTc < stressLT(1, 0) And stressLT(1, 0) < FTt And Abs(stressLT(2, 0)) < FLTs Then
        fracture = fracture
    Else
        fracture = fracture + 1
    End If
Next j

3次元配列である\( \overline{\bf Q} \)を，行列演算のFunctionに入れるために2次元配列tmp()に格納していることと，破断しているかどうかの判定で，破断しているときにfractureに1を足していることに注意してほしい

「破断している」の条件分岐

もしどこかの層が破断していれば，fractureが0でないはずなので，合力を1刻み分元に戻し，合力の刻みを0.1倍にする

さらに，有効桁数のカウンターも1つ増やしておく

If fracture > 0 Then
    stress0(0, 0) = stress0(0, 0) - dN '合力を1刻み分元に戻す
    dN = dN * 0.1 '合力の刻みを0.1倍する
    num = num + 1 '有効桁数のカウンターを1つ増やす
End If

「有効桁数を超えた」の条件分岐

合力の値が有効桁数を満たした場合，合力の無限ループを抜ける

If num > sf Then
   　Exit For
End If

ここまでが合力のループの中の処理である

結果の出力

計算した破断合力をエクセルシートに貼り付ける

'結果の出力
Range("D36") = stress0(0, 0)

プログラムの実行

今回作成したプログラムを実際に実行してみる

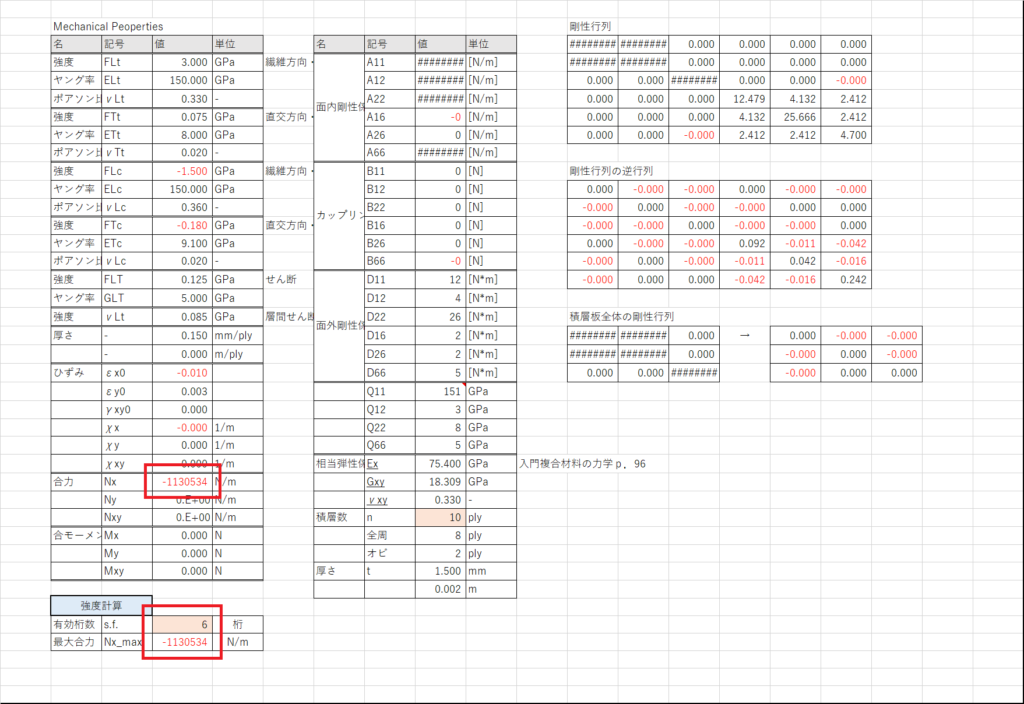
(90/45/0/-45/0)sの積層構成で有効桁数6桁で計算してみると結果は \( N_x\) =-1'130'534[N/m] になる

この値をセルD27に入力してみると，

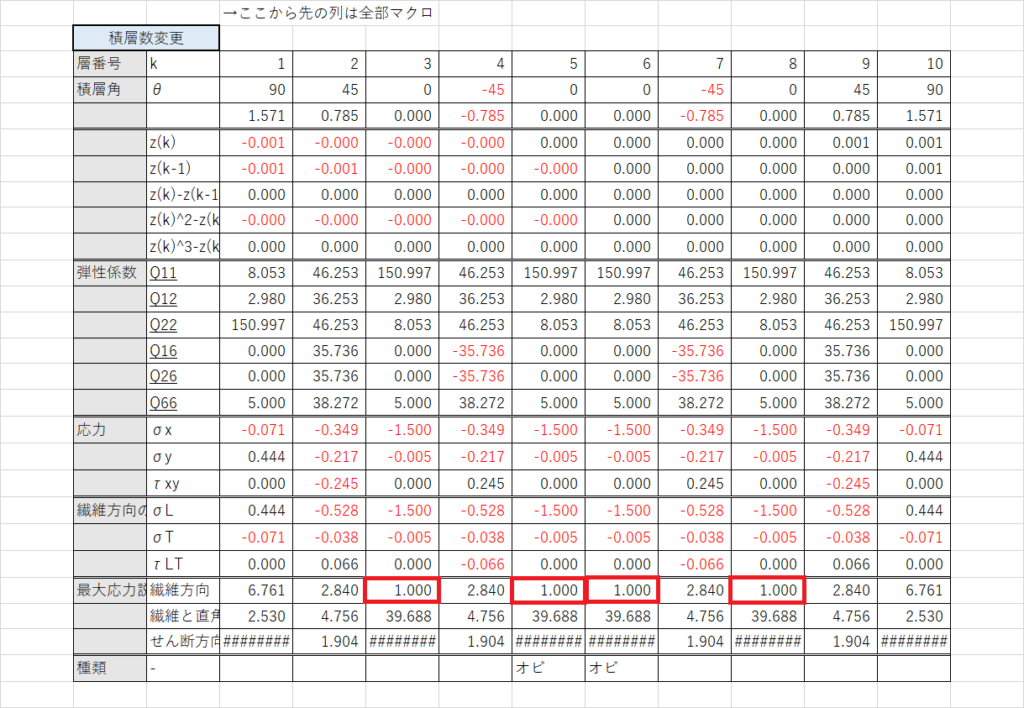
0度層が繊維方向に破断する直前であることがわかる

まとめ

解析的には求まりそうにない値も，プログラミングを使った力業なら計算できることもある

"力 is power."

この世の真理である

↓次の記事

↓記事一覧