古典積層理論

古典積層理論を用いてCFRPの積層板の剛性を計算する

目的とフローチャート

今回の目的は，古典積層理論を用いて，任意の積層構成の剛性を求めることである

以下の資料を参考にする

複合材料の力学序説　古今書院　以下，(序)

入門複合材料の力学　培風館　以下，(入)

式の導出について詳しく知りたい人は上にあげた本を読んでもらいたい

どちらかというと複合材料の力学序説が分かりやすい

この記事での式番号は，あとで参照しやすいように参考文献と同じものを利用する

古典積層理論に関する数式

使用する式は以下のとおりである（L:Longitudinal/繊維方向、T:Transverse/繊維の直角方向）

直交異方性板の主軸方向のフックの法則　(序)p.82

\begin{eqnarray}
\left[ \begin{array}{c}
\sigma_L \\ \sigma_T \\ \tau_{LT}
\end{array} \right] =
\left[ \begin{array}{ccc}
Q_{11} &Q_{12} &0 \\ Q_{12}&Q_{22}&0 \\ 0&0&Q_{66}
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_L \\ \varepsilon_T \\ \gamma_{LT}
\end{array} \right]
\tag{4.50}
\end{eqnarray}

\begin{eqnarray}
Q_{11}&=& \frac{E_L}{1-\nu_{LT}\nu_{TL}} \\
Q_{22}&=& \frac{E_T}{1-\nu_{LT} \nu_{TL}} \\
Q_{12}&=& \frac{\nu_{TL} E_L}{1-\nu_{LT} \nu_{TL}}= \frac{\nu_{LT} E_T}{1-\nu_{LT} \nu_{TL}} \\
Q_{66}&=&G_{LT} \tag{4.51}
\end{eqnarray}

任意方向のフックの法則　(序)p.84

\begin{eqnarray}
\left[ \begin{array}{c} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{array} \right] =
\left[ \begin{array}{ccc}
\overline{Q_{11}} & \overline{Q_{12}} & \overline{Q_{16}} \\
\overline{Q_{12}}& \overline{Q_{22}}& \overline{Q_{26}} \\
\overline{Q_{16}}& \overline{Q_{26}}& \overline{Q_{66}}
\end{array} \right]
\left[ \begin{array}{c} \varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{array} \right]
\tag{4.50}
\end{eqnarray}

\begin{eqnarray}
Q_{11}&=& Q_{11}l^4+2(Q_{12}+2Q_{66})l^2 m^2+Q_{22}m^4 \\
Q_{12}&=& Q_{12}(l^4+m^4)+(Q_{11}+Q_{22}-4Q_{66})l^2 m^2 \\
Q_{22}&=& Q_{11}m^4+2(Q_{12}+2Q_{66})l^2 m^2+Q_{22}l^4 \\
Q_{16}&=& (Q_{11}-Q_{12}-2Q_{66})l^3 m-(Q_{22}-Q_{12}-2Q_{66})l m^3 \\
Q_{26}&=& (Q_{11}-Q_{12}-2Q_{66})l m^3-(Q_{22}-Q_{12}-2Q_{66})l^3 m \\
Q_{66}&=& (Q_{11}+Q_{22}-2Q_{12}-2Q_{66})l^2 m^2+Q_{66}(l^4+m^4)
\tag{4.58}
\end{eqnarray}

ただし，\(l=cos{\theta}, m=sin{\theta} \)

積層板の剛性行列　(序)p.126

\begin{eqnarray}
A_{ij}&=& \sum_{k=1}^n (\overline{Q_{ij}})_k (z_{k}-z_{k-1}) \\
B_{ij}&=& \frac{1}{2} \sum_{k=1}^n (\overline{Q_{ij}})_k (z_{k}^2-z_{k-1}^2) \\
D_{ij}&=& \frac{1}{3} \sum_{k=1}^n (\overline{Q_{ij}})_k (z_{k}^3-z_{k-1}^3) \\
(i, j)&=&1, 2, 6 \\
\tag{6.8}
\end{eqnarray}

\begin{eqnarray}
\left[ \begin{array}{c}
N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy}
\end{array} \right] =
\left[ \begin{array}{cccccc}
A_{11} & A_{12} & A_{16} & B_{11} & B_{12} & B_{16} \\
A_{12} & A_{22} & A_{26} & B_{12} & B_{22} & B_{26} \\
A_{16} & A_{26} & A_{66} & B_{16} & B_{26} & B_{66} \\
B_{11} & B_{12} & B_{16} & D_{11} & D_{12} & D_{16} \\
B_{12} & B_{22} & B_{26} & D_{12} & D_{22} & D_{26} \\
B_{16} & B_{26} & B_{66} & D_{16} & D_{26} & D_{66} \\
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x^0 \\
\varepsilon_y^0 \\
\gamma_{xy}^0 \\
\chi_x^0 \\
\chi_y^0 \\
\chi_{xy}^0
\end{array} \right]
\tag{6.9}
\end{eqnarray}

積層板の剛性行列，コンプライアンス行列　(入)p.96

\begin{eqnarray}
\left[ \begin{array}{c}
\overline{\sigma_x} \\
\overline{\sigma_y} \\
\overline{\tau_{xy}}
\end{array} \right] =
\left[ \begin{array}{ccc}
\overline{Q_{11}} & \overline{Q_{12}} & \overline{Q_{16}} \\
\overline{Q_{12}}& \overline{Q_{22}}& \overline{Q_{26}} \\
\overline{Q_{16}}& \overline{Q_{26}}& \overline{Q_{66}}
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x \\
\varepsilon_y \\
\gamma_{xy}
\end{array} \right]
\tag{13}
\end{eqnarray}

\begin{eqnarray}
\left[ \begin{array}{c}
\varepsilon_x \\
\varepsilon_y \\
\gamma_{xy}
\end{array} \right] =
\left[ \begin{array}{ccc}
\overline{S_{11}} & \overline{S_{12}} & \overline{S_{16}} \\
\overline{S_{12}} & \overline{S_{22}} & \overline{S_{26}} \\
\overline{S_{16}} & \overline{S_{26}} & \overline{S_{66}}
\end{array} \right]
\left[ \begin{array}{c}
\overline{\sigma_x} \\
\overline{\sigma_y} \\
\overline{\tau_{xy}}
\end{array} \right]
\tag{14}
\end{eqnarray}

積層板の相当弾性率　(入)p.96

\begin{eqnarray}
\overline{E_x}&=& \frac{1}{\overline{S_{11}}} \tag{15} \\
\overline{\nu_{xy}}&=& -\frac{\overline{S_{12}}}{\overline{S_{11}}} \tag{16} \\
\overline{G_{xy}}&=& \frac{1}{\overline{S_{66}}} \tag{17} \\
\end{eqnarray}

積層板の弾性率の計算は大した計算量じゃないのでマクロではなくシートで計算を行う

フローチャートを以下に示す

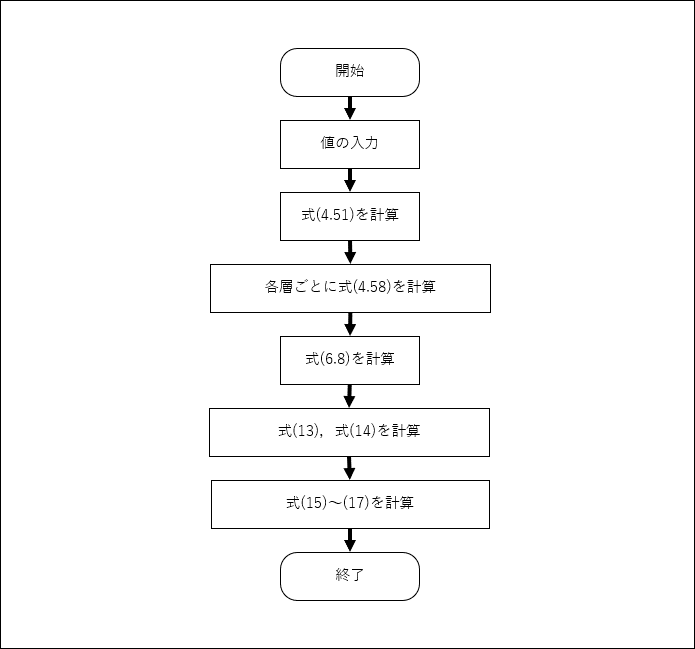
テンプレートファイルのダウンロード

エクセルの数式などの参考になるようにテンプレートファイルを添付しておく

エクセルシートの解説

それでは実際に解説していく

値の入力

セルD4～D19にCFRPのカタログなどから繊維方向/直角方向と圧縮/引張方向のヤング率，強度，ポアソン比とプリプレグ1枚の厚さを入力する（t:tensile/引張、c:compressive/圧縮）

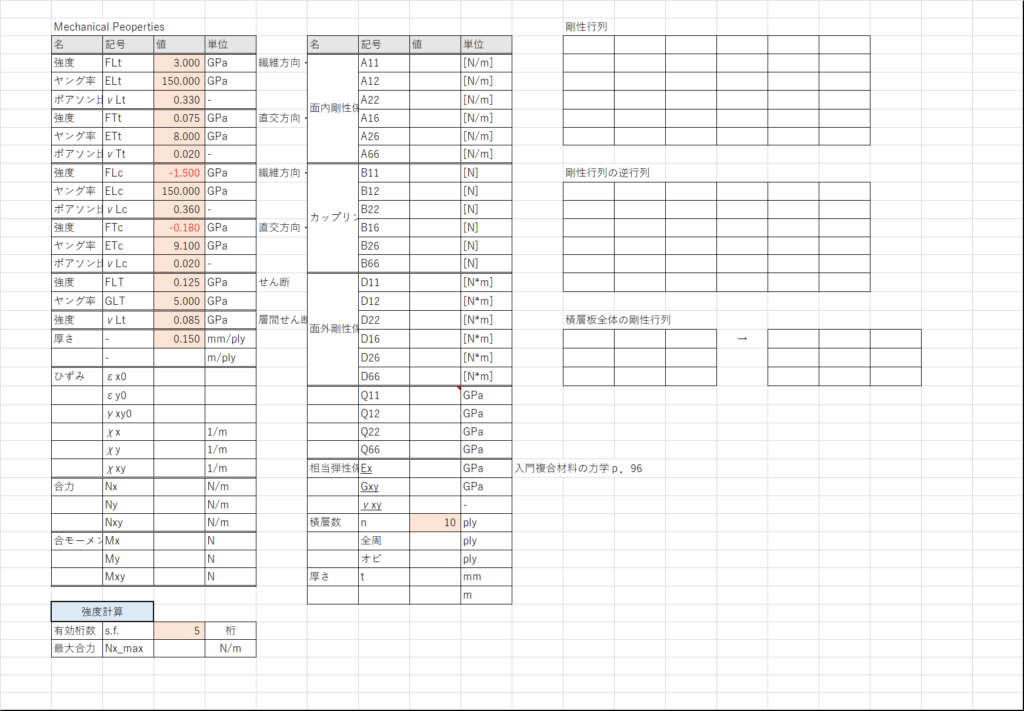
D20でプリプレグ厚さをm/plyに変換する

セルX4～に任意の積層構成を入力して，X5～で[deg]から[rad]に変換する

RADIANS関数を使うとよい

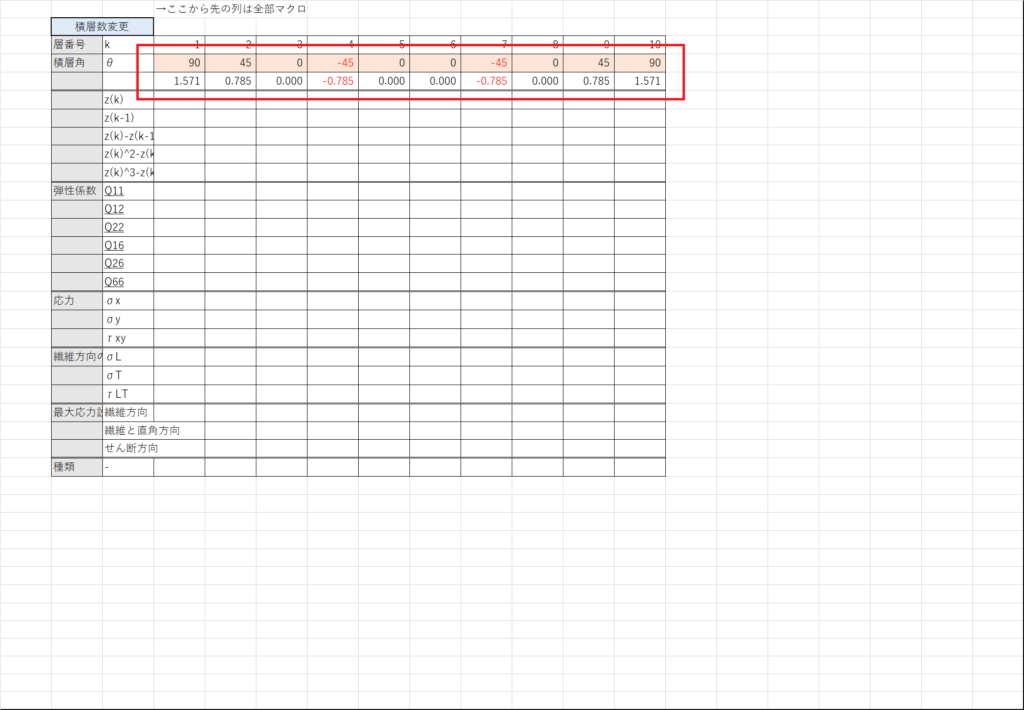
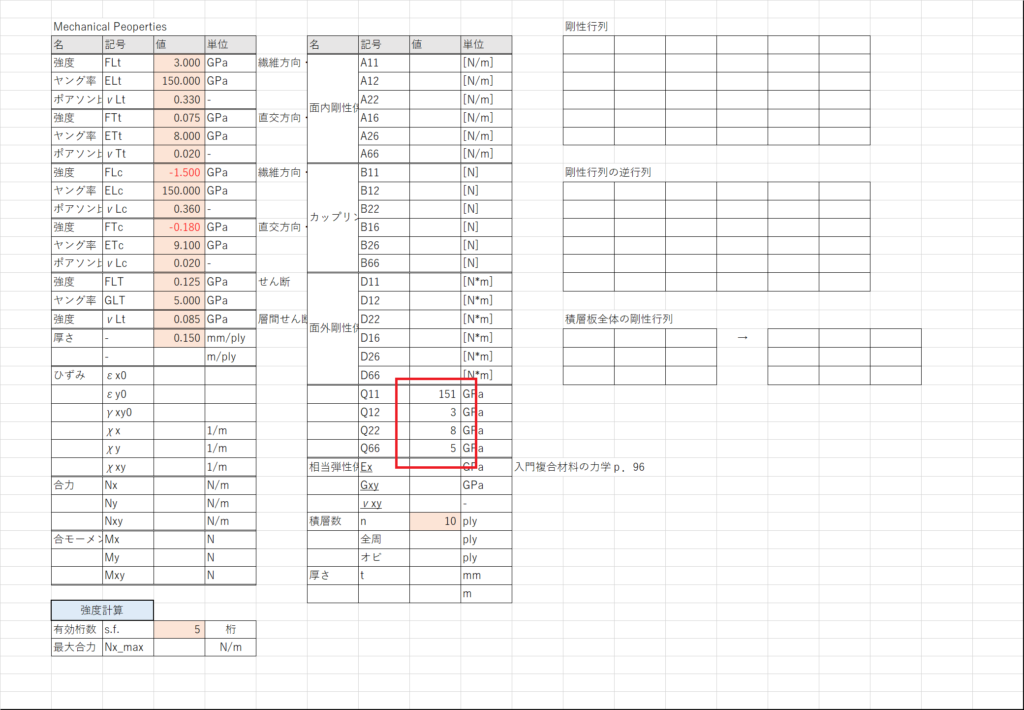
式(4.51)を入力

セルI22～I25に式(4.51)を入力する

\begin{eqnarray}
Q_{11}&=& \frac{E_L}{1-\nu_{LT}\nu_{TL}} \\
Q_{22}&=& \frac{E_T}{1-\nu_{LT} \nu_{TL}} \\
Q_{12}&=& \frac{\nu_{TL} E_L}{1-\nu_{LT} \nu_{TL}}= \frac{\nu_{LT} E_T}{1-\nu_{LT} \nu_{TL}} \\
Q_{66}&=&G_{LT} \tag{4.51}
\end{eqnarray}

各層ごとに式(4.58)を入力する

セルX11～X15～に式(4.58)を入力する

\begin{eqnarray}
Q_{11}&=& Q_{11}l^4+2(Q_{12}+2Q_{66})l^2 m^2+Q_{22}m^4 \\
Q_{12}&=& Q_{12}(l^4+m^4)+(Q_{11}+Q_{22}-4Q_{66})l^2 m^2 \\
Q_{22}&=& Q_{11}m^4+2(Q_{12}+2Q_{66})l^2 m^2+Q_{22}l^4 \\
Q_{16}&=& (Q_{11}-Q_{12}-2Q_{66})l^3 m-(Q_{22}-Q_{12}-2Q_{66})l m^3 \\
Q_{26}&=& (Q_{11}-Q_{12}-2Q_{66})l m^3-(Q_{22}-Q_{12}-2Q_{66})l^3 m \\
Q_{66}&=& (Q_{11}+Q_{22}-2Q_{12}-2Q_{66})l^2 m^2+Q_{66}(l^4+m^4)
\tag{4.58}
\end{eqnarray}

オートフィルと絶対参照，相対参照をうまく使おう

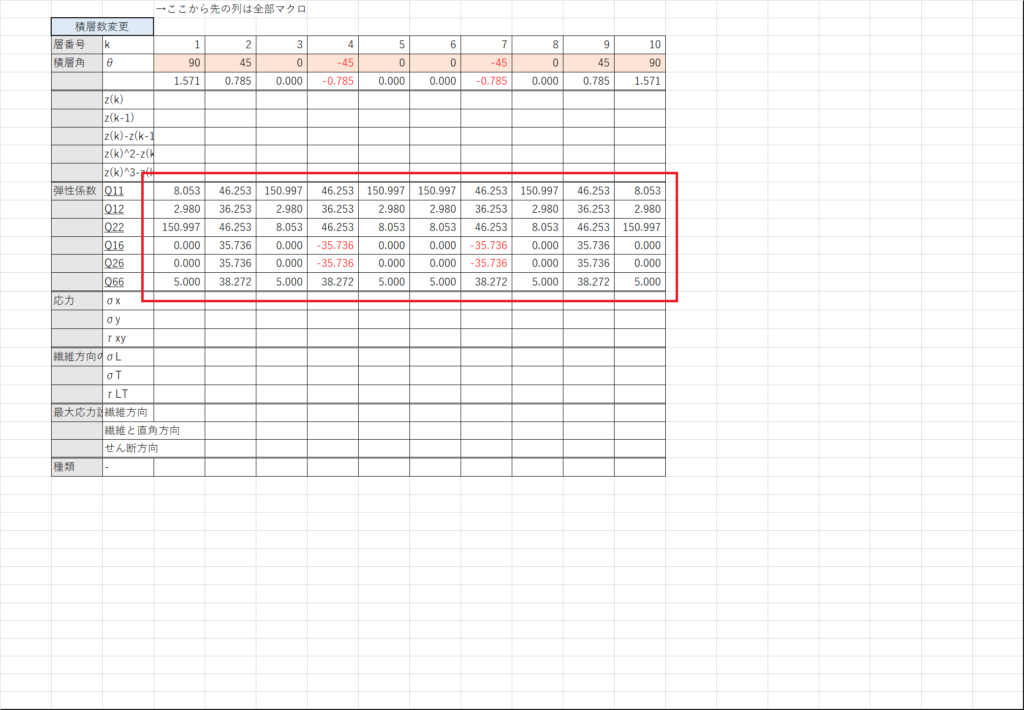
式(6.8)を入力する

まず，X6~X10~でzの値を計算する

z座標の定義は(序)p.125に書いてある

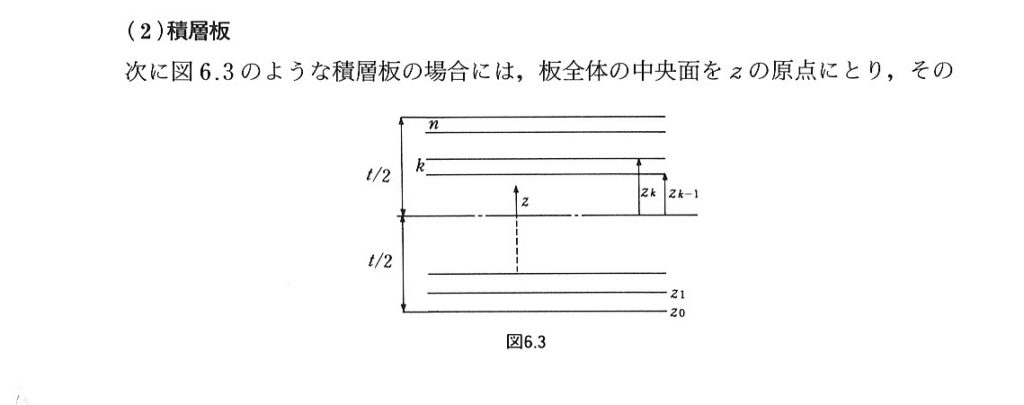
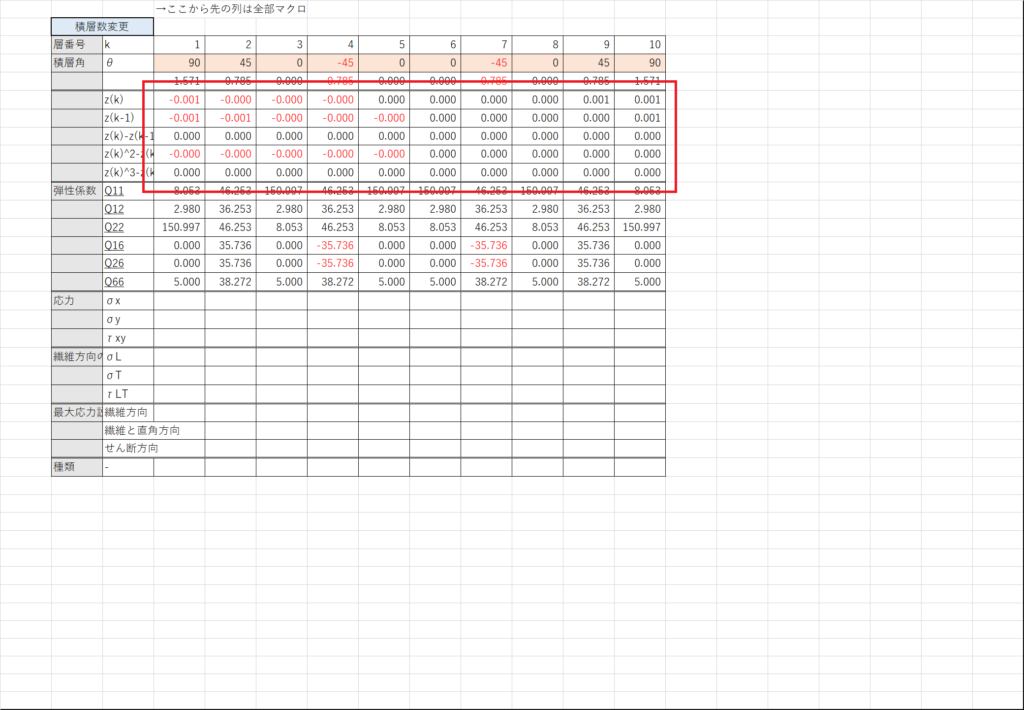
セルI4~I21に式(6.8)を入力する

\begin{eqnarray}
A_{ij}&=& \sum_{k=1}^n (\overline{Q_{ij}})_k (z_{k}-z_{k-1}) \\
B_{ij}&=& \frac{1}{2} \sum_{k=1}^n (\overline{Q_{ij}})_k (z_{k}^2-z_{k-1}^2) \\
D_{ij}&=& \frac{1}{3} \sum_{k=1}^n (\overline{Q_{ij}})_k (z_{k}^3-z_{k-1}^3) \\
(i, j)&=&1, 2, 6 \\
\tag{6.8}
\end{eqnarray}

Σの計算には積の和を計算してくれる便利な関数，SUMPRODUCT関数を使うといい

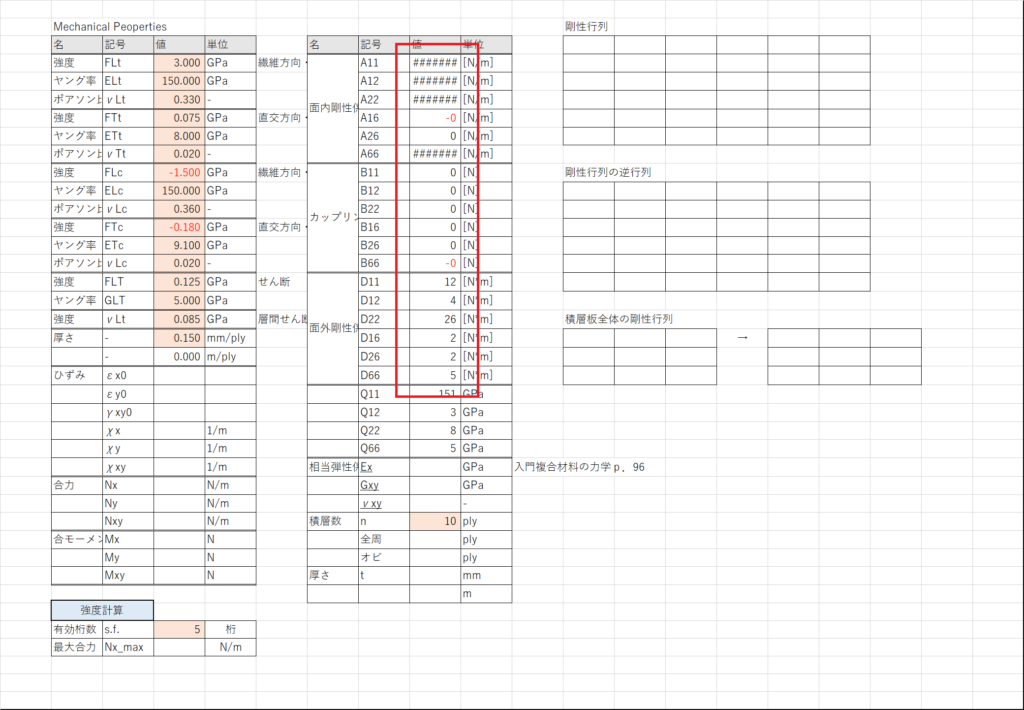
今回の積層構成は(90/45/0/-45/0)sの疑似等方性対称積層なので，A16，A26，B11～B66が0になっていることを確認する

ついでにセルL3～Q8に行列形式で剛性係数を入力しておく．普通に「＝」を使ったらいい

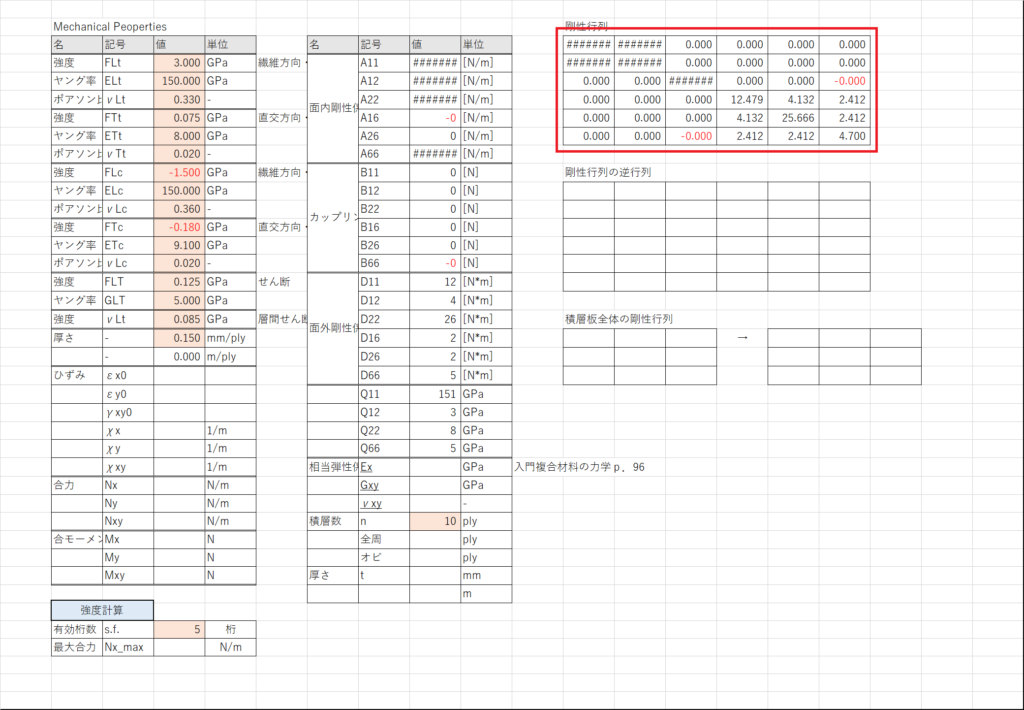
式(13)，(14)を計算する

式(13)を計算する

\begin{eqnarray}
\left[ \begin{array}{c}
\overline{\sigma_x} \\
\overline{\sigma_y} \\
\overline{\tau_{xy}}
\end{array} \right] =
\left[ \begin{array}{ccc}
\overline{Q_{11}} & \overline{Q_{12}} & \overline{Q_{16}} \\
\overline{Q_{12}}& \overline{Q_{22}}& \overline{Q_{26}} \\
\overline{Q_{16}}& \overline{Q_{26}}& \overline{Q_{66}}
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x \\
\varepsilon_y \\
\gamma_{xy}
\end{array} \right]
\tag{13}
\end{eqnarray}

式(13)の \( \overline{\bf Q} \)は，剛性係数 \( \overline{\bf A} \) を板厚で除したものなので，まず板厚をI32~I33で計算する（単位注意）

板厚はプリプレグ厚さ×積層数である

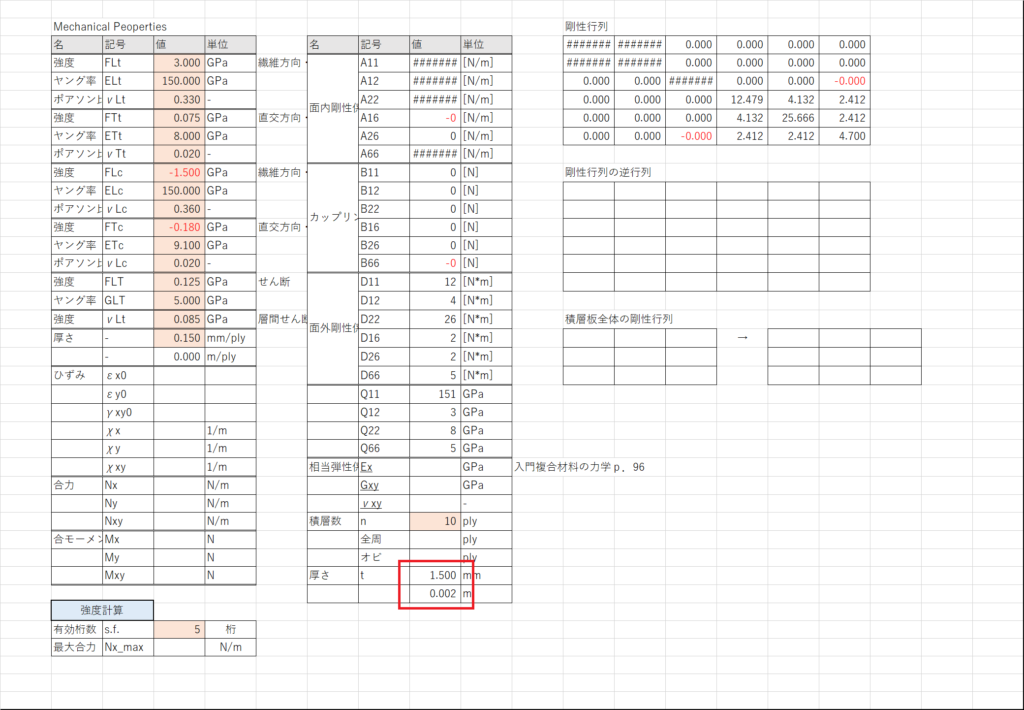
セルL19～L21に\( \overline{\bf Q} \)を計算する

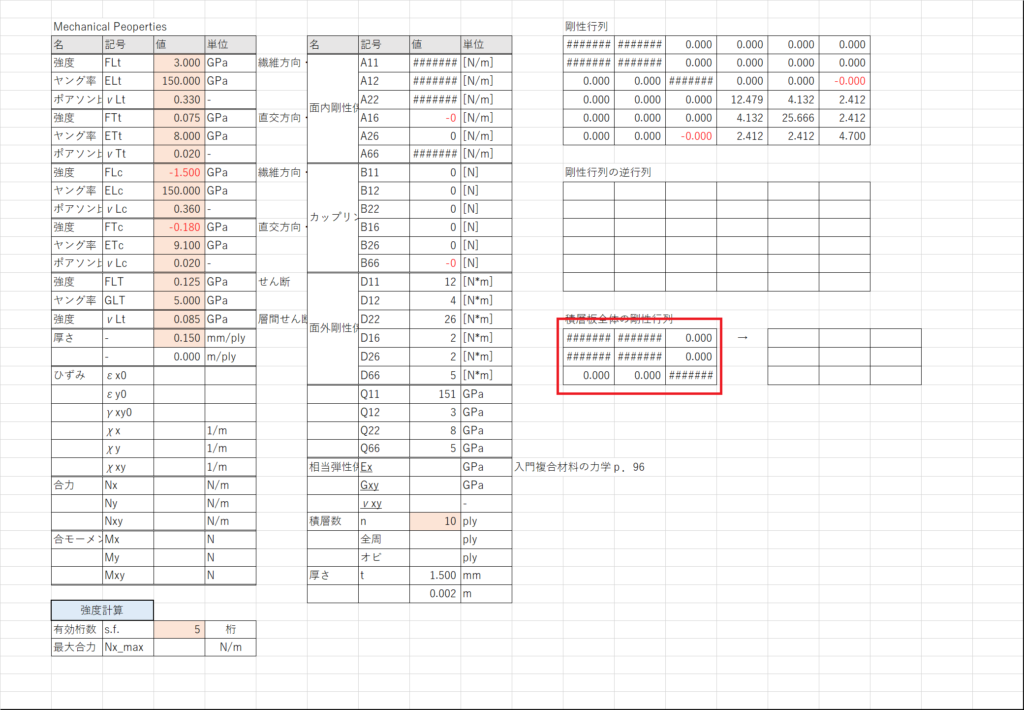
セルP19～P21に式(14)を計算する

\begin{eqnarray}
\left[ \begin{array}{c}
\varepsilon_x \\
\varepsilon_y \\
\gamma_{xy}
\end{array} \right] =
\left[ \begin{array}{ccc}
\overline{S_{11}} & \overline{S_{12}} & \overline{S_{16}} \\
\overline{S_{12}} & \overline{S_{22}} & \overline{S_{26}} \\
\overline{S_{16}} & \overline{S_{26}} & \overline{S_{66}}
\end{array} \right]
\left[ \begin{array}{c}
\overline{\sigma_x} \\
\overline{\sigma_y} \\
\overline{\tau_{xy}}
\end{array} \right]
\tag{14}
\end{eqnarray}

逆行列の計算はMINVERSE関数を使うといい

MINVERSE関数は，セルP19～P21を選択してから「F2」キーで「＝MINVERSE(L19:N21)」と入力し，「Ctrl＋Shift＋Enter」で入力を確定する

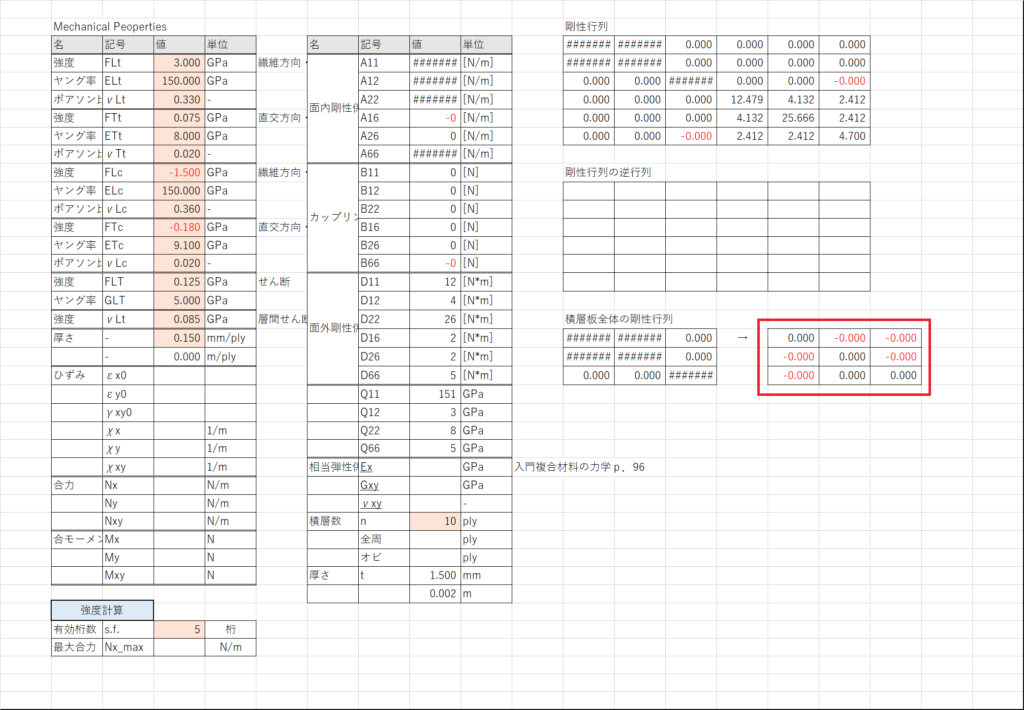
式(15)～式(17)を計算する

セルI26～I28に式(15)~式(17)を計算する

\begin{eqnarray}
\overline{E_x}&=& \frac{1}{\overline{S_{11}}} \tag{15} \\
\overline{\nu_{xy}}&=& -\frac{\overline{S_{12}}}{\overline{S_{11}}} \tag{16} \\
\overline{G_{xy}}&=& \frac{1}{\overline{S_{66}}} \tag{17} \\
\end{eqnarray}

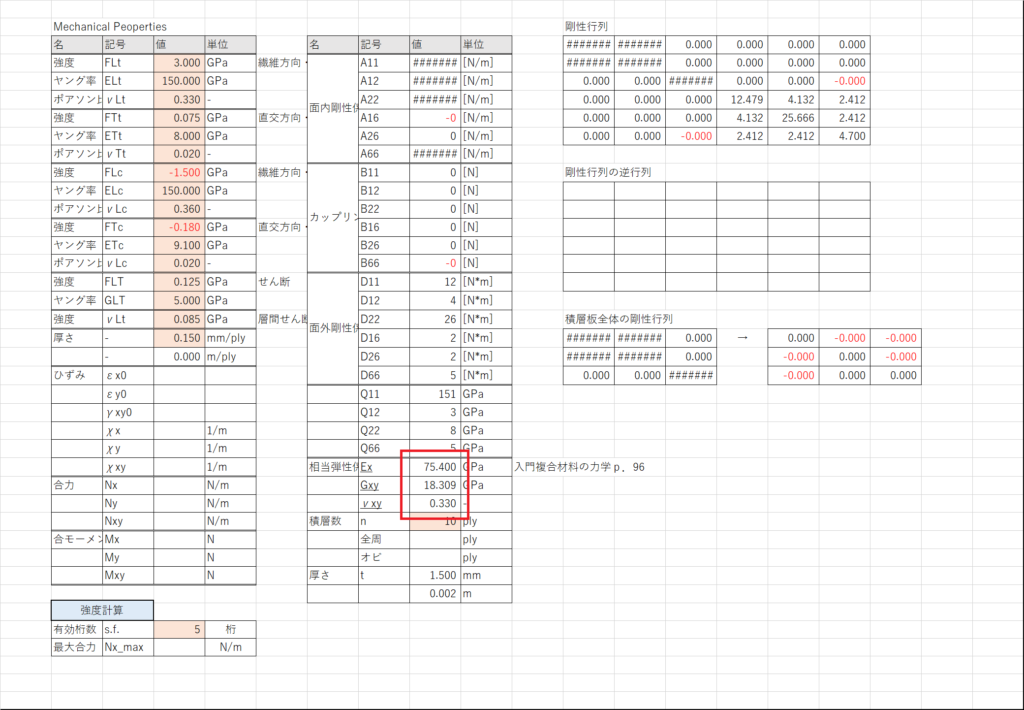
これで今回の目的は達成できた

まとめ

あくまで相当弾性特性は「CFRP積層板を等方性だとしたら・・・」という仮定に基づいたものである

桁のたわみ計算にしてもそうだが，これからの議論はすべてこの「(ほんとは違うけど，)等方性だとしたら」という仮定に基づいて進んでいく

そんなあいまいさが許せない人はぜひ「有限要素法」で検索してみよう

↓次の記事

最大応力説で積層板の強度を計算する

最大応力説を使って積層板の強度を計算する

mtkbirdman.com

2019.10.03

↓鳥人間コンテストの機体設計のまとめ記事

設計シート作りの記事一覧

設計シートを作りについて説明した記事の一覧

mtkbirdman.com

2021.06.13