桁の断面二次モーメント,ねじれ定数,断面積,周長などを計算する
目的
今回の目的は,スパーの断面二次モーメント,ねじれ定数,断面積,周長などを計算することである
「え?スパーの断面係数って中空パイプの公式に値を代入するだけじゃん?」と考えたそこのあなた,世の中には楕円断面長軸強化積層とかいう桁を自作しているチームがあることを頭の片隅にでも覚えておいてほしい
原理の解説
よく材料力学の教科書の公式集に載っているような断面二次モーメントや断面二次極モーメントの公式は,特定の断面にしか適用することができない
たとえば円形断面だとしても,長軸に強化積層を施してしまえば周方向に厚さが不均一になってしまうので中空パイプの公式を用いることはできなくなる
そんなときはどうすればいいかというと,定義式に従って愚直に計算していくしかない
断面二次モーメントの定義式
任意の断面について,断面二次モーメントは次の式で計算できる
\begin{eqnarray}
I_x&=&\int_A y^2 dA \\
I_y&=&\int_A x^2 dA
\tag{1}
\end{eqnarray}
ねじれ定数の定義式
ここでは,断面二次極モーメントではなく,閉断面モノコック構造のねじれ定数を考える
任意の閉断面モノコック構造について,ねじれ定数は次の式で計算できる
\begin{eqnarray}
J=\frac{4A_m^2}{\oint \frac{ds}{t}}
\tag{2}
\end{eqnarray}
ここで\( A_m \)は断面の中心線が囲む面積,\( t \)は板厚,\( \oint ds \)は断面に沿った周回積分を表す
このねじれ定数はねじれ角を\( \phi \),トルクを\( T \),横弾性係数を\( G \),棒の長さを\( l \)とすると次の関係式が成り立つ値である
\begin{eqnarray}
\phi=\frac{Tl}{GJ}
\end{eqnarray}
筆者がこの公式を勉強したのが大学の講義の配布資料なので参考文献を載せることはできないが,Google先生で「閉断面薄肉構造 ねじれ定数」とでも検索すれば次のようなサイトが出てくる
このサイトの式(7.19)に,先に紹介したものと同じ式が出てくるので,詳しく勉強したい人は参照してみるといいかもしれない
定式化
式(1),式(2)のように,今回求めたい値は断面についての面積分や線積分で計算できることがわかった
積分で計算できるということは,断面を無限に小さく分割したものの総和で表せるということでもある
ここからは,楕円断面について式(1),式(2)を計算するための定式化を説明していく
※長軸の長さと短軸の長さを同じにすれば円形断面にも適用できる
式(1),式(2)を計算するにあたって求めなければいけない変数は\(x\),\(y\),\(dA\),\(A_m\),\(t\),\(ds\)なので,これらの変数を順次考えていく
まず,楕円は次の方程式で表すことができる
\begin{eqnarray}
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\tag{3}
\end{eqnarray}
ここで,\(r\),\(\theta\)からなる極座標を導入すると\(x\),\(y\)は次のように表せる
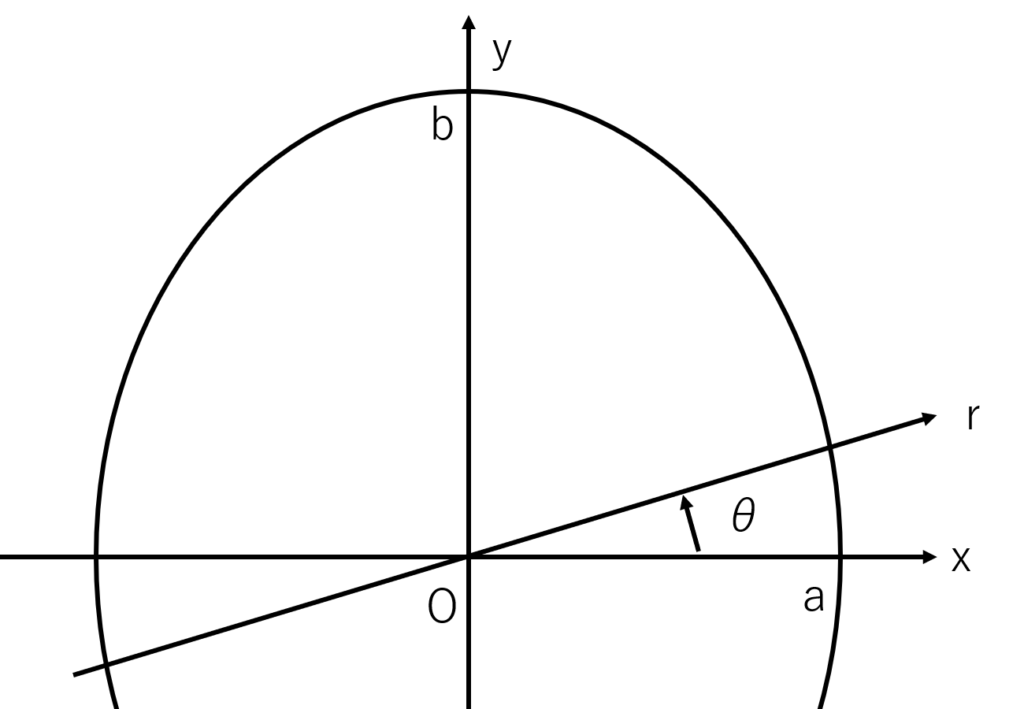
\begin{eqnarray}
x&=&a\cos{\theta} \\
y&=&b\sin{\theta} \\
r&=&\sqrt{x^2+y^2}
\tag{4}
\end{eqnarray}
このまま真円のときのように式を展開していってもいいが,一応楕円なのでr軸に対する垂線と楕円の接線のなす角を考慮しておく
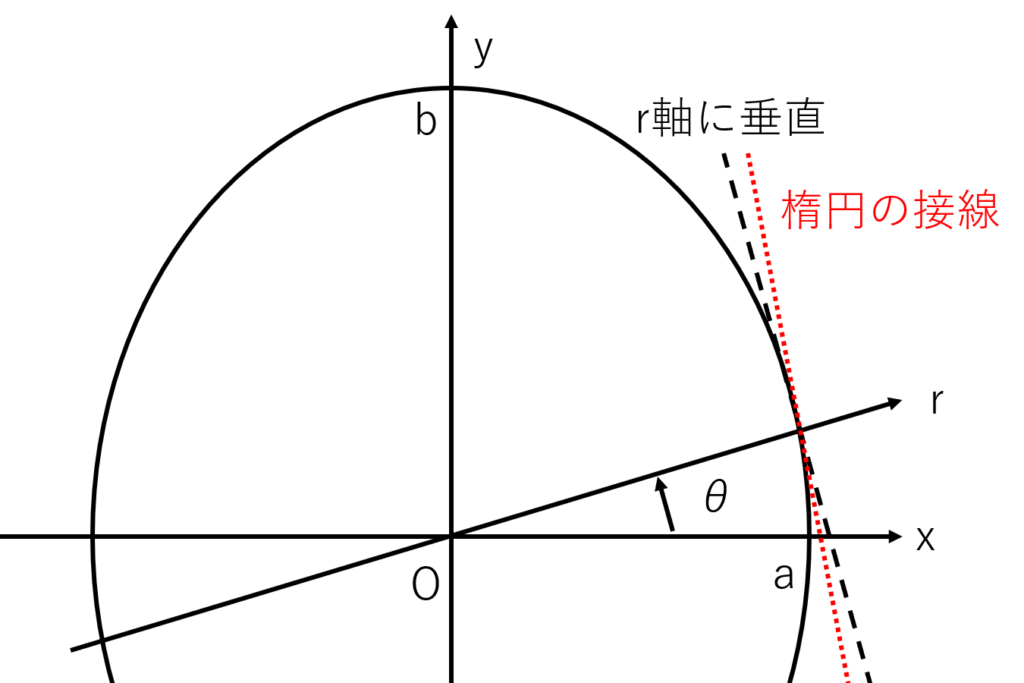
楕円の接線の公式より,楕円上の点\((x_0, y_0)\)における楕円の接線の傾き\(\phi(<0)\)は次の式で表せる
\begin{eqnarray}
\phi&=&\arctan{(-\frac{b^2}{a^2}\frac{x_0}{y_0})}
\tag{5}
\end{eqnarray}
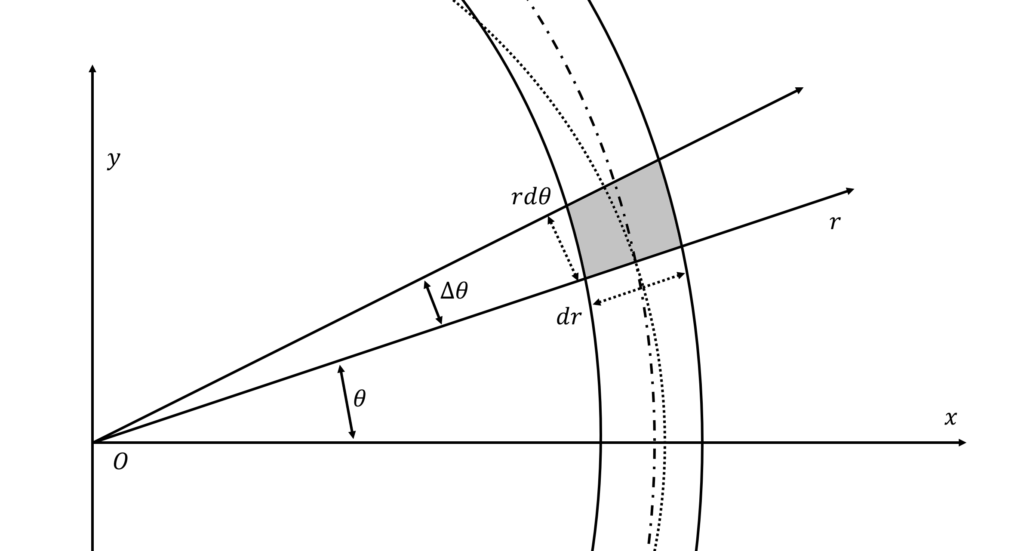
x軸から角度θ回転させたr軸と楕円との交点を点\((x_0, y_0)\)として,さらに微小角度\(\Delta\theta\)回転させた場合を考える
点\((x_0, y_0)\)付近を拡大してみる
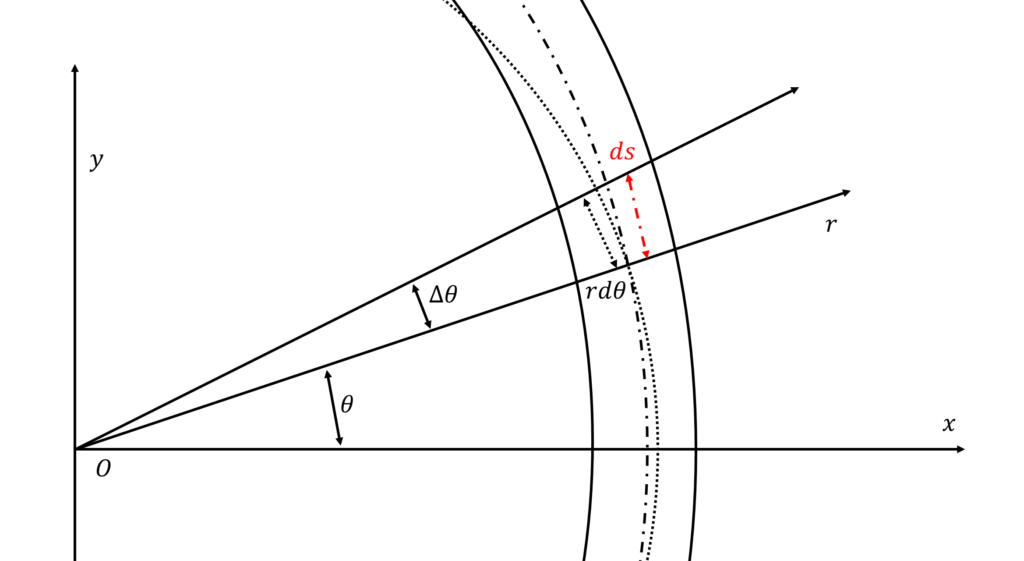
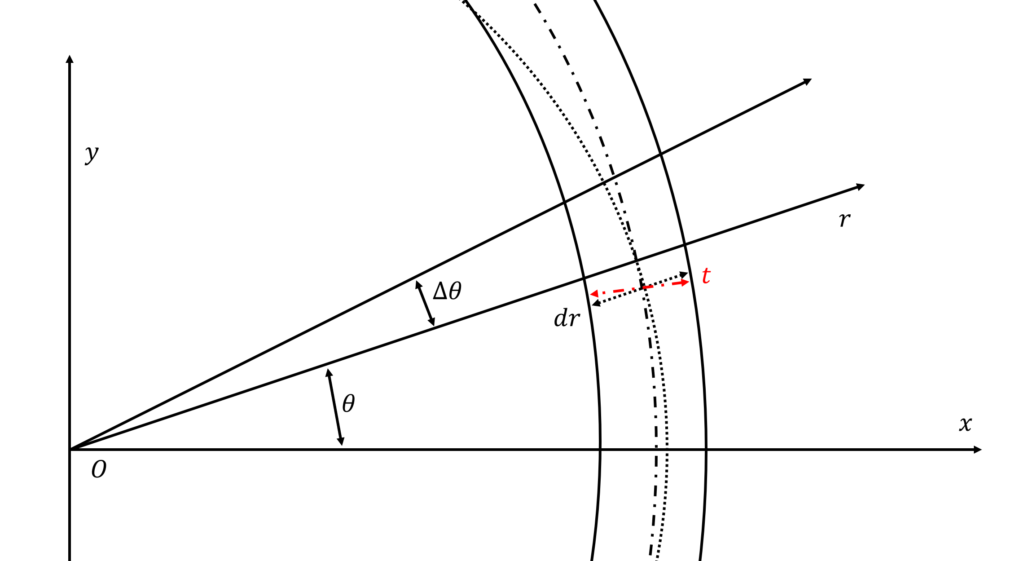
\(rd\theta\)と\(ds\),\(dr\)と\(t\)の関係は,点線(真円)と一点鎖線(楕円)の接線のなす角が\(\theta-(\frac{\pi}{2}+\phi)\)であることを考慮すると次のようになる
\begin{eqnarray}
ds&=&\frac{dr}{\cos{(\theta-\frac{\pi}{2}-\phi)}}
\tag{6} \\
t&=&dr\cos{(\theta-\frac{\pi}{2}-\phi)}
\tag{7}
\end{eqnarray}
\(dA\)は,下図の灰色に塗られた部分で,次の式で表される
\begin{eqnarray}
dA&=&rdrd\theta(=tds)
\tag{8}
\end{eqnarray}
\(A_m\)はただの楕円の面積なので,唯一積分を使わずに求めることができ,次の式で表される
\begin{eqnarray}
A_m&=&\pi a b
\tag{9}
\end{eqnarray}
これで必要な変数はすべて計算できるようになった
ちなみに,周の長さ\(L\)と断面積\(A\)は次の式で計算できる
\begin{eqnarray}
L&=&\oint_C ds
\tag{9} \\
A&=&\int_A dA
\tag{10}
\end{eqnarray}
フローチャート
今回のプログラムはFunctionとし,引数と戻り値はそれぞれ次のようにする
'引数
Dim ai As Double '楕円内径短半軸 [mm]
Dim bi As Double '楕円内径長半軸 [mm]
Dim ao As Double '楕円外径短半軸 [mm]
Dim bo As Double '楕円外径長半軸 [mm]
Dim num As Integer '周方向分割数'戻り値(配列に格納)
Dim Ix As Double '断面二次モーメント [mm^4]
Dim Iy As Double '断面二次モーメント [mm^4]
Dim Cj As Double 'ねじれ定数 [mm^4]
Dim Area As Double '断面積 [mm^2]
Dim Am As Double '中心線が囲む面積 [mm^2]
Dim Length As Double '中心線の周長 [mm]また,断面の対称性より,周回積分は\(0<\theta<\frac{\pi}{2}\)の範囲のみで行い,計算の最後に4倍する
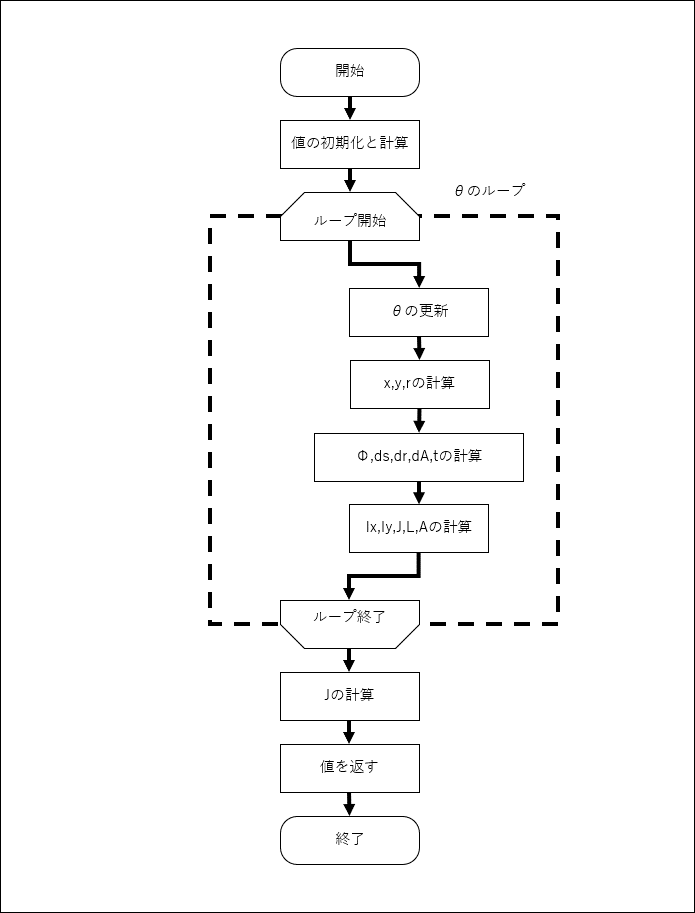
フローチャートを以下に示す
Functionについて知りたい人はこちら
≫【VBA入門】Functionの使い方(呼び出し、引数、戻り値)
プログラムの解説
それでは実際に解説していく
使用する変数
マクロで使用する変数を以下に示す
'変数の宣言
'内径
Dim r_in As Double '極座標r
Dim x_in As Double 'x座標
Dim y_in As Double 'y座標
'外径
Dim r_out As Double '極座標r
Dim x_out As Double 'x座標
Dim y_out As Double 'y座標
'中心線(cl:center line)
Dim a_cl As Double '楕円短半軸 [mm]
Dim b_cl As Double '楕円長半軸 [mm]
Dim r_cl As Double '極座標r
Dim x_cl As Double 'x座標
Dim y_cl As Double 'y座標
'その他
Dim thickness As Double '板厚t [mm]
Dim dr As Double '内径と外径のrの差 [mm]
Dim ds As Double '周方向の微小要素ds=rdθ [mm]
Dim dA As Double '微小面積dA=rdrdθ [mm^2]
Dim theta As Double '極座標θ [rad]
Dim dtheta As Double '微小角度dθ [rad]
Dim phi As Double '楕円の接線の角度 [rad]
Dim data() As Double 'エクセルシートに貼り付ける用の配列
Dim pi As Double '円周率π
'戻り値
Dim Ix As Double '断面二次モーメント [mm^4]
Dim Iy As Double '断面二次モーメント [mm^4]
Dim J As Double 'ねじれ定数 [mm^4]
Dim Area As Double '断面積 [mm^2]
Dim Am As Double '中心線が囲む面積 [mm^2]
Dim Length As Double '中心線の周長 [mm]
'カウンター
Dim i As Integer値の初期化と計算
基本的にExcel VBAは初期値として0が入っているが,ほかの言語 (某tranとか) では最初に値を初期化しておかないといけない言語もあるので,習慣として初期化しておく
値の計算は式を見てもらえればわかると思う
'値の初期化と計算
pi = 4 * Atn(1) '[rad]
theta = 0 '[rad]
dtheta = (pi / 2) / num '微小角度dθ [rad]
a_cl = (a_in + a_out) / 2 '楕円短半軸 [mm]
b_cl = (b_in + b_out) / 2 '楕円長半軸 [mm]
Ix = 0 '断面二次モーメント [mm^4]
Iy = 0 '断面二次モーメント [mm^4]
J = 0 'ねじれ定数 [mm^4]
Area = 0 '断面積 [mm^2]
Am = pi * a_cl * b_cl '中心線が囲む面積 [mm^2]
Length = 0 '中心線の周長 [mm]\(\theta\)のループ
とくに注意することはない
'θのループ
For i = 0 To num
(ループ内の処理)
Next i
\(\theta\)の更新
特に注意することはない
'θの更新
theta = dtheta * i\(x\),\(y\),\(r\)の計算
式(4)を計算する
\begin{eqnarray}
x&=&a\cos{\theta} \\
y&=&b\sin{\theta} \\
r&=&\sqrt{x^2+y^2}
\tag{4}
\end{eqnarray}
'x,y,rの計算
'内径
x_in = a_in * Cos(theta)
y_in = b_in * Sin(theta)
r_in = Sqr(x_in ^ 2 + y_in ^ 2)
'外径
x_out = a_out * Cos(theta)
y_out = b_out * Sin(theta)
r_out = Sqr(x_out ^ 2 + y_out ^ 2)
'中心線
x_cl = a_cl * Cos(theta)
y_cl = b_cl * Sin(theta)
r_cl = Sqr(x_cl ^ 2 + y_cl ^ 2)\(\phi\),\(ds\),\(dr\) ,\(t\) ,\(dA\)の計算
式(5)~(8)を計算する
\begin{eqnarray}
\phi&=&\arctan{(-\frac{b^2}{a^2}\frac{x_0}{y_0})}
\tag{5} \\
ds&=&\frac{dr}{\cos{(\theta-\frac{\pi}{2}-\phi)}}
\tag{6} \\
t&=&dr\cos{(\theta-\frac{\pi}{2}-\phi)}
\tag{7} \\
dA&=&rdrd\theta(=tds)
\tag{8}
\end{eqnarray}
\(\theta=0\)のときのみ式(5)の\(\arctan{}\)の中身の分母が0になってしまうため場合分けを行っている
'phi,ds,dr,dA,tの計算
If theta = 0 Then
phi = pi / 2
ds = r_cl * dtheta
Else
phi = Atn(-((b_cl / a_cl) ^ 2) * (x_cl / y_cl)) '[rad]
ds = r_cl * dtheta / Cos(theta - pi / 2 - phi)
End If
dr = r_out - r_in
thickness = dr * Cos(theta - pi / 2 - phi)
dA = r_cl * dtheta * dr\(I_x\),\(I_y\),\(J\) ,\(L\) ,\(A\)の計算
式(1),(2),(9),(10)を計算する
\begin{eqnarray}
I_x&=&\int_A y^2 dA \\
I_y&=&\int_A x^2 dA
\tag{1} \\
J&=&\frac{4A_m^2}{\oint \frac{ds}{t}}
\tag{2} \\
L&=&\oint_C ds
\tag{9} \\
A&=&\int_A dA
\tag{10}
\end{eqnarray}
ただし,\(J\)のみ\(\oint \frac{ds}{t}\)を計算し,ループの外で式(2)を計算する
'Ix,Iy,J,L,Aの計算
Ix = Ix + y_cl * y_cl * dA
Iy = Iy + x_cl * x_cl * dA
J = J + (ds / thickness) '∫ds/t
Length = Length + ds
Area = Area + dAこれでループの中の処理は終了である
\(J\)の計算
式(2)を計算する
\begin{eqnarray}
J&=&\frac{4A_m^2}{\oint \frac{ds}{t}}
\tag{2}
\end{eqnarray}
対称性より,\(\oint \frac{ds}{t}\)を4倍することを忘れないように
'Jの計算
J = (4 * Am * Am) / (J * 4) '[mm^4]値を返す
それぞれの値を4倍して配列に格納したあと,Functionに値を返す
'断面係数を配列に格納
ReDim data(5)
data(0) = Ix * 4
data(1) = Iy * 4
data(2) = J
data(3) = Area * 4
data(4) = Am
data(5) = Length * 4
'関数に値を返す
Section_Modulus = data()プログラムの解説はこれで終了である
プログラムの実行
今回作成したプログラムを実際に実行してみる
せっかくなので,解析的に値が求められる真円パイプで,分割数を変化させながら値がどのように収束していくかを確認してみる
実行用のコードはこれ
Sub 楕円分割数比較()
'パラメーター
Const num_max As Integer = 15
'変数の宣言
'内径
Dim ai As Double '楕円短半軸 [mm]
Dim bi As Double '楕円長半軸 [mm]
'外径
Dim ao As Double '楕円短半軸 [mm]
Dim bo As Double '楕円長半軸 [mm]
'中心線
Dim num As Integer '周方向分割数
Dim data() As Double 'エクセルシートに貼り付ける用の配列
Dim tmp() As Double 'Functionから値を受け取る用の配列
'カウンター
Dim i As Integer
'タイマーの変数
Dim startTime As Double
Dim endTime As Double
Dim processTime As Double
Application.ScreenUpdating = False '画面更新の非表示
startTime = Timer '開始時間取得
'値の入力
bo = 50 '[mm]
ao = 50 '[mm]
bi = 49 '[mm]
ai = 49 '[mm]
'配列の要素数を決定
ReDim data(num_max, 6)
For i = 2 To num_max
num = 2 ^ i - 2 '分割数の計算
tmp() = Section_Modulus(ai, bi, ao, bo, num) '断面係数の計算
'計算結果を貼り付け用配列に格納
data(i, 0) = num
For j = 0 To 5
data(i, j + 1) = tmp(J)
Next j
Next i
Range("B43:H" & 43 + num_max & "") = data '結果の出力
endTime = Timer '終了時間取得
processTime = endTime - startTime '処理時間計算
MsgBox "計算が終了しました" & vbCrLf & "処理時間:" & processTime '処理時間表示
End Sub実行時間は約0.17秒で,計算結果は次のようになった
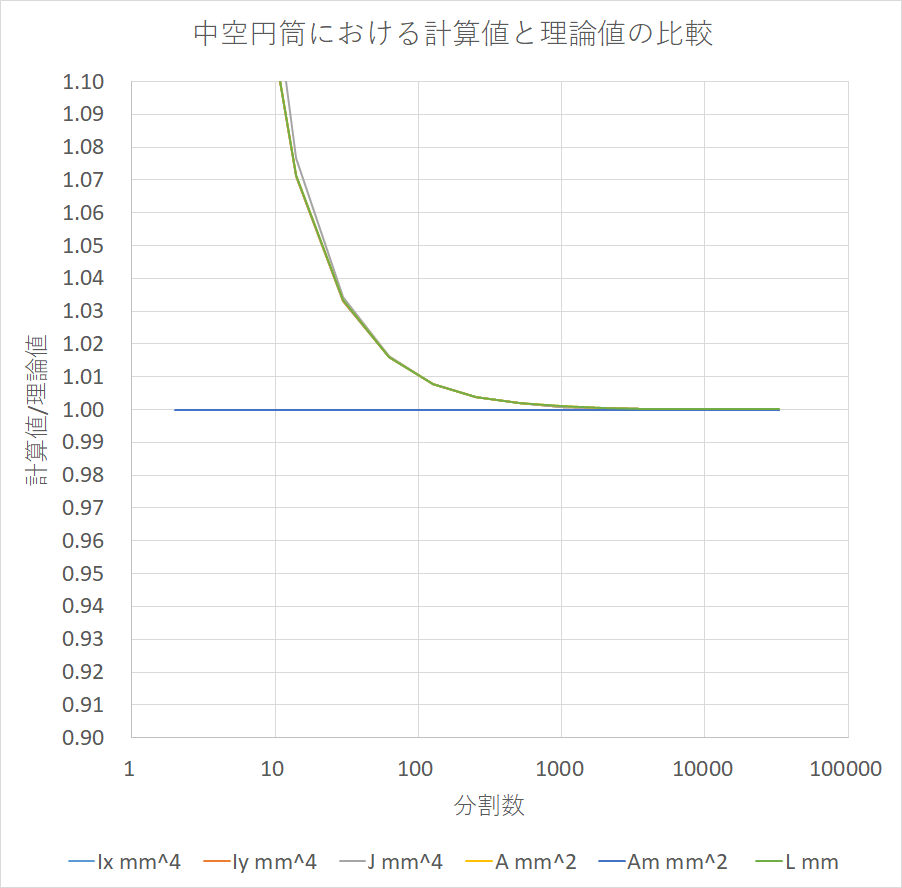
おおよそ分割数が1000を超えれば誤差はほぼなくなる
ついでに短軸/長軸比が0.8の中空楕円筒でも,解析的に値を求めることができる断面積と囲む面積で分割数による値の収束を計算してみた
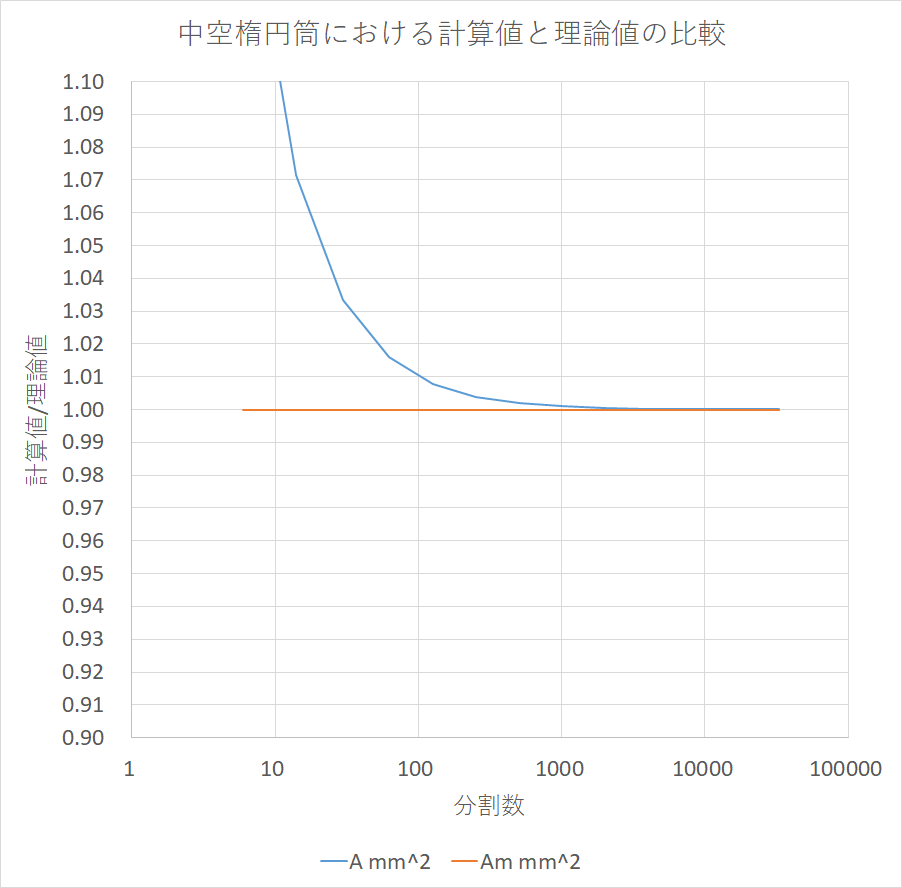
結果は真円のときとほぼ同じになった
まとめ
今回のプログラムはどこかの教科書の内容をただ写したものではなく,かなり筆者のオリジナリティが高いコードなので,使ってみるときは自分でよく妥当性を確認することをおすすめする
もしどこかに間違いを見つけたら一大事なので,大至急コメント欄で教えてほしい
↓次の記事
↓記事一覧





コメント