翼型の圧力分布を理解するために、いろいろな翼型の圧力分布を紹介する
はじめに
翼型の圧力分布を理解するために、圧力分布の基本といろいろな翼型の圧力分布を紹介する
↓翼型の基本についてはこちら(他サイト)
翼型の形状定義 ー 翼型の形状を決める2つのパラメータ(翼厚とキャンバー) | 鳩ぽっぽ
↓圧力分布の可視化はXFOILを使用し、流線の可視化は境界要素法を使用した
実際に使ったExcelマクロのダウンロードはこの記事の一番最後で
参考文献
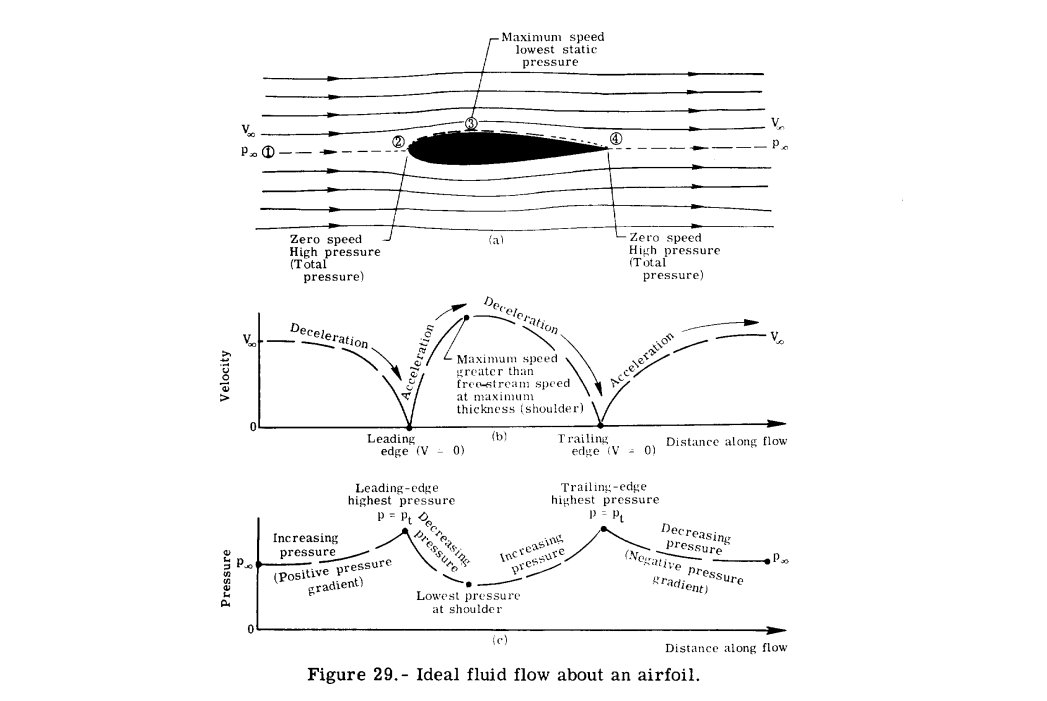
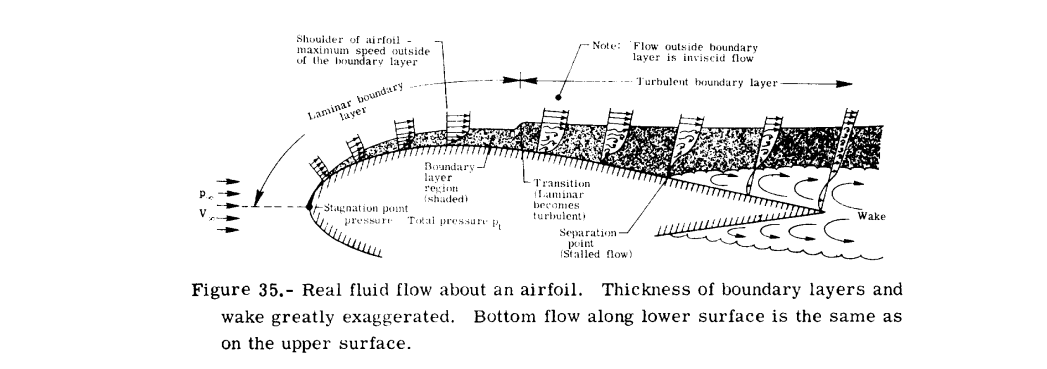
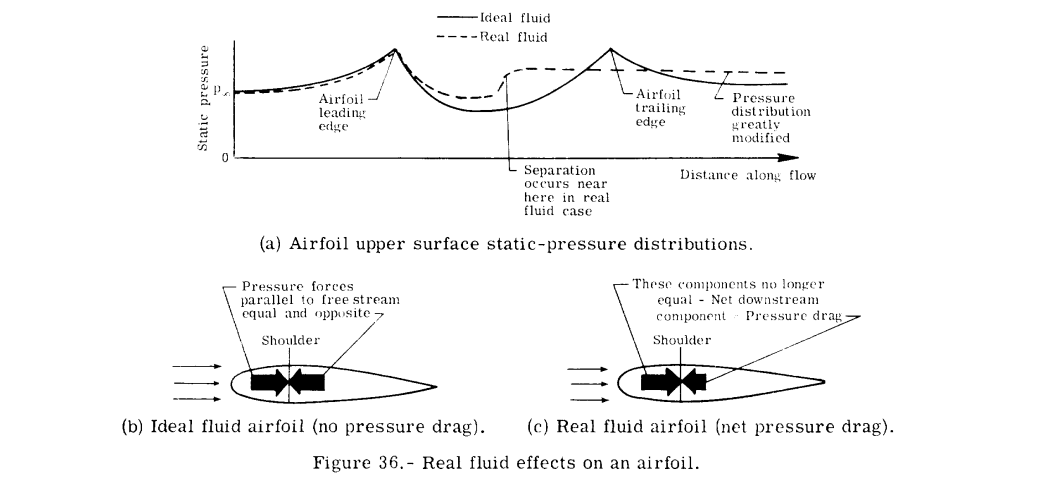
↓ポテンシャル流れ/粘性流れ
Investigation of low-speed turbulent separated flow around airfoils - NASA Technical Reports Server (NTRS)
Described is a low-speed wind tunnel experiment to measure the flowfield around a two-dimensional airfoil operating clos...
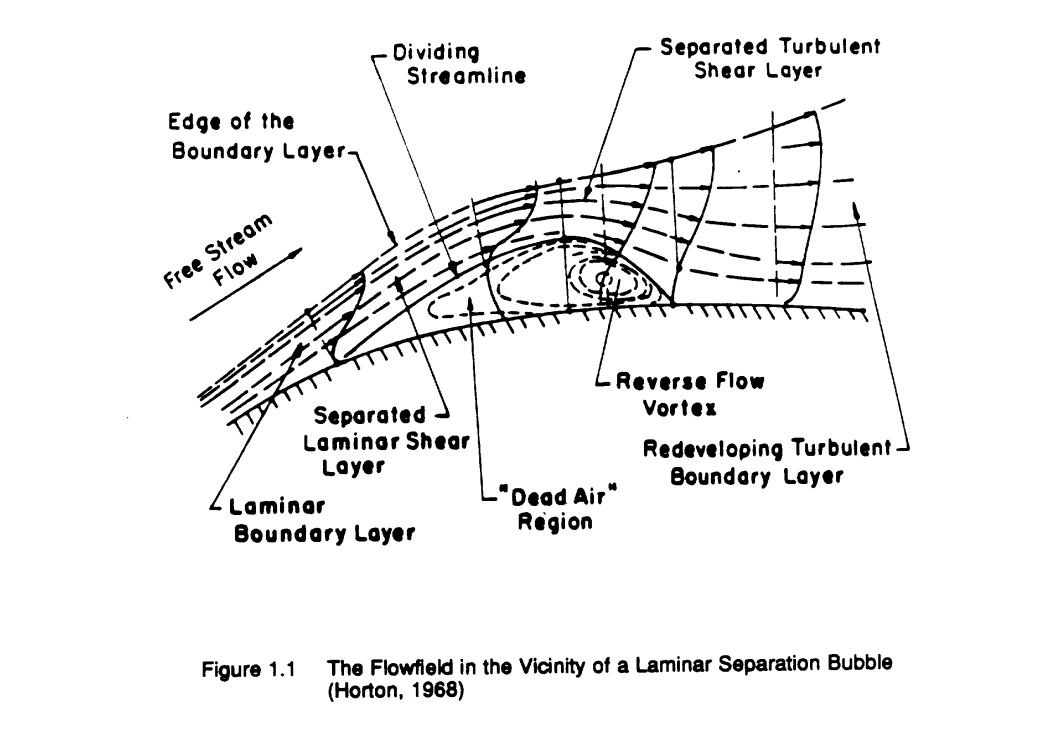
↓低レイノルズ数流れ/境界層剥離
Experimental measurements of the laminar separation bubble on an Eppler 387 airfoil at low Reynolds numbers - NASA Technical Reports Server (NTRS)
An experimental investigation was conducted to measure the flow velocity in the boundary layer of an Eppler 387 airfoil....
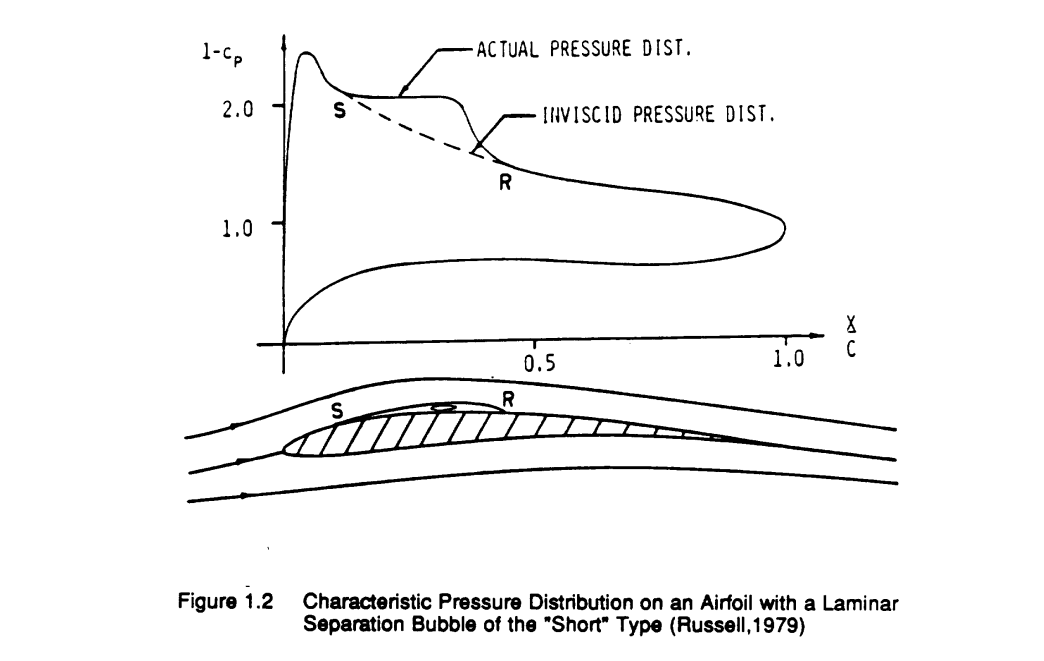
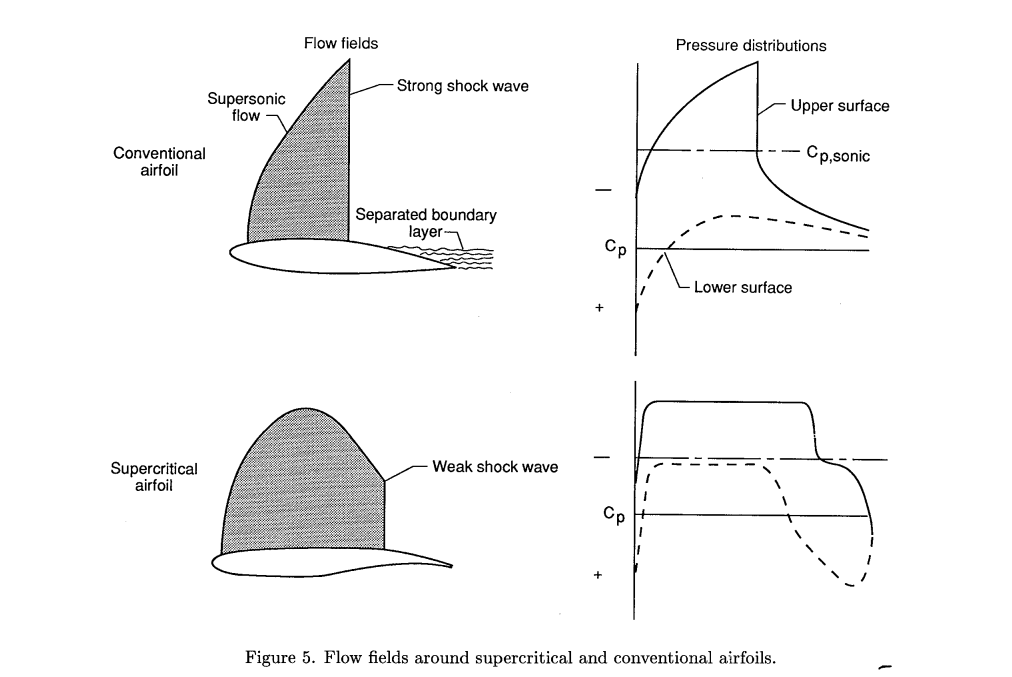
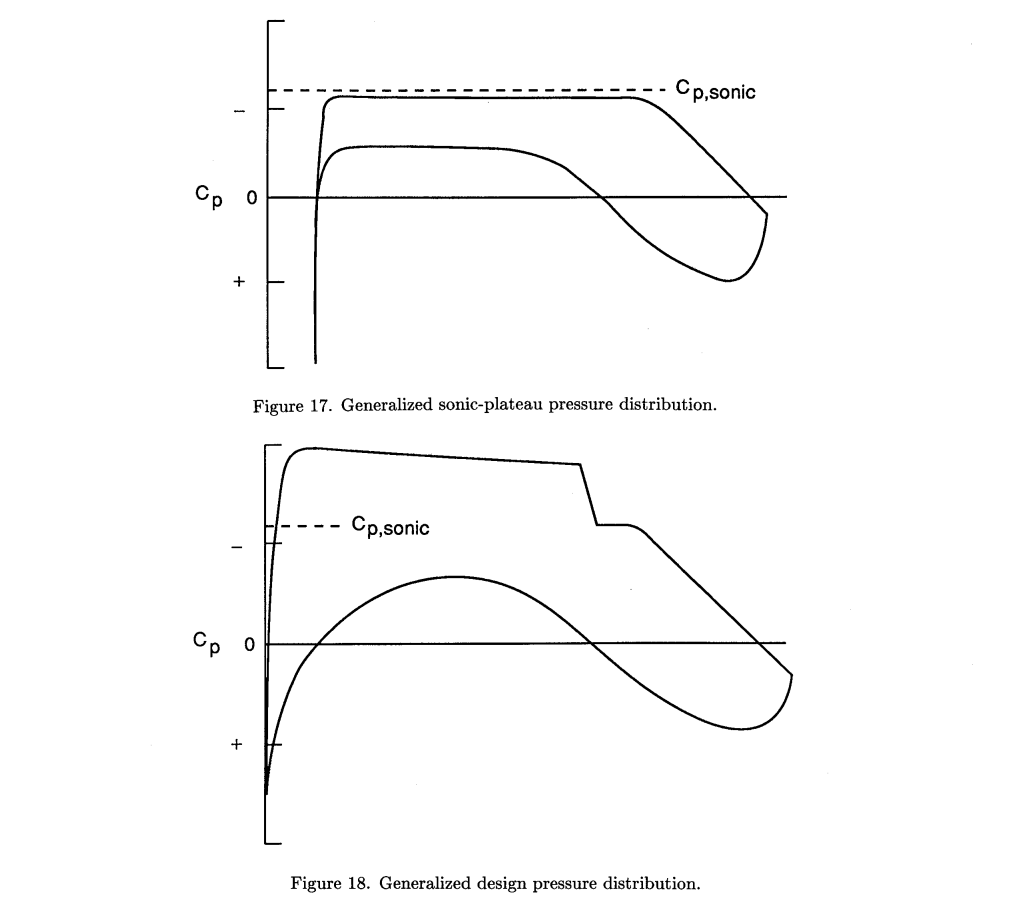
↓超臨界翼
NASA supercritical airfoils: A matrix of family-related airfoils - NASA Technical Reports Server (NTRS)
The NASA supercritical airfoil development program is summarized in a chronological fashion. Some of the airfoil design ...
対称翼(NACA0012)
XFOIL解析条件
- Re=1E7
- Mach=0
- xtr=(0,0) ※前縁で強制遷移
ゼロ揚力角
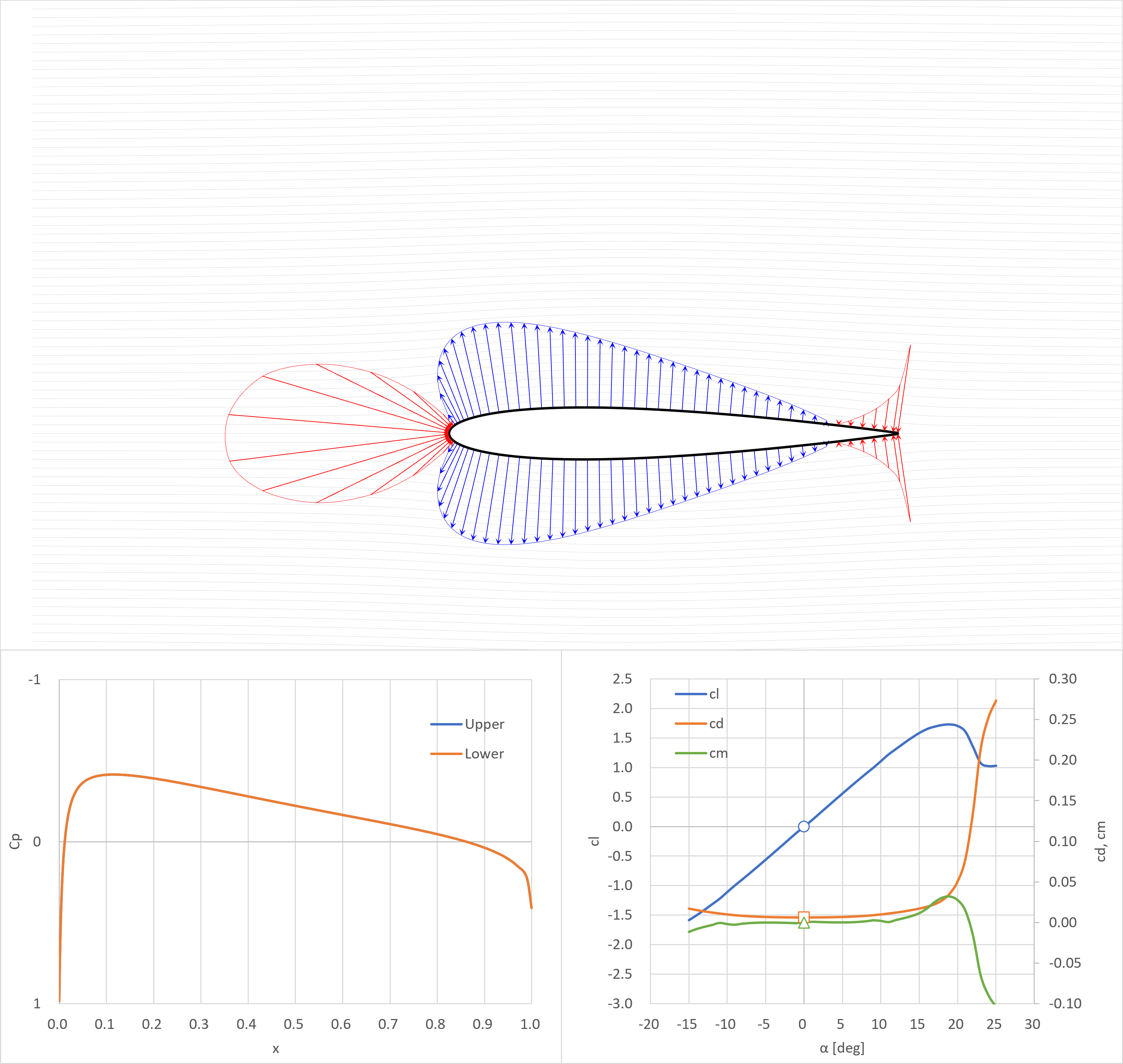
- 上下対象の圧力分布
- 後縁のCp=0.409
cl=0.5
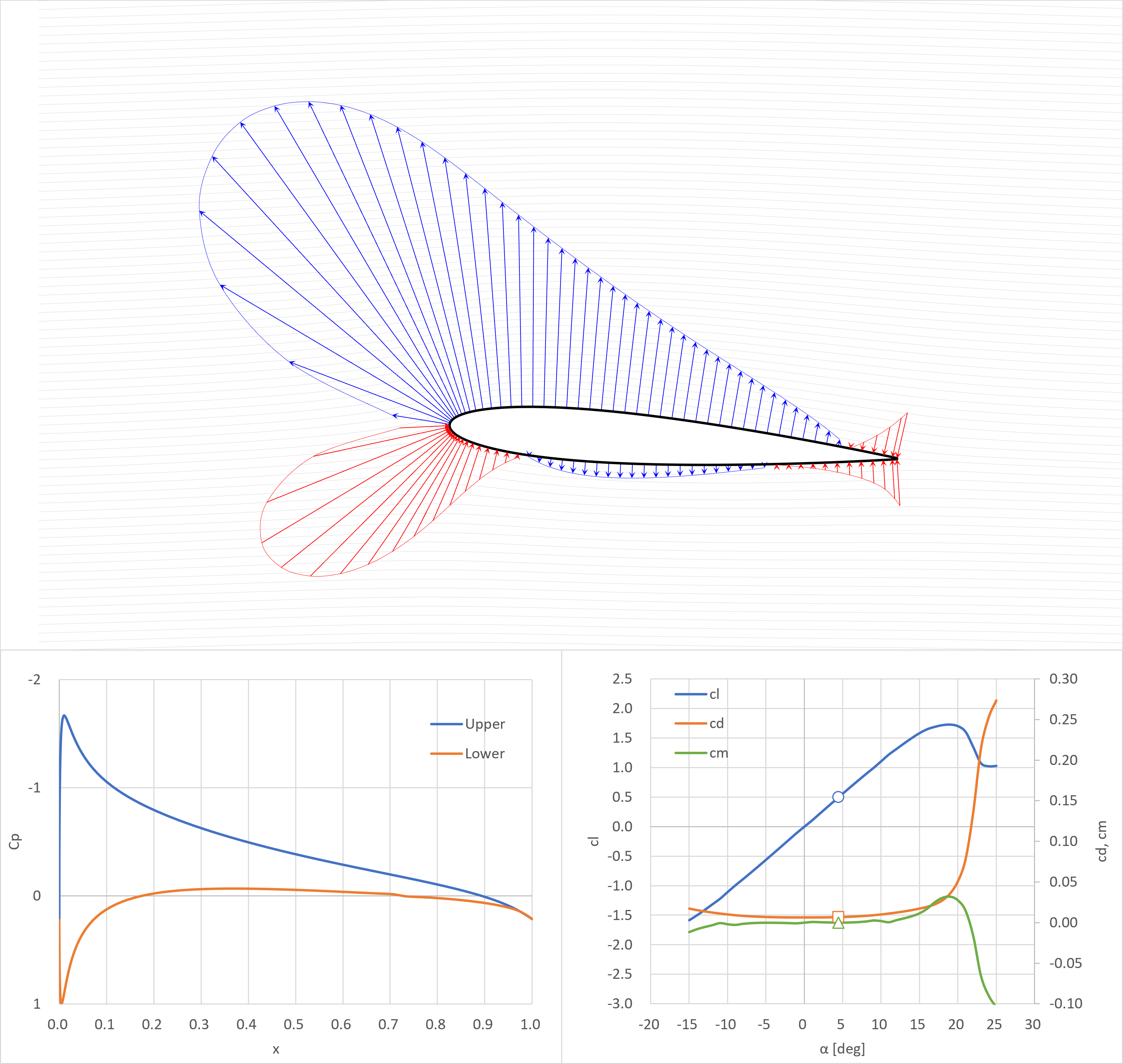
cl=1.0
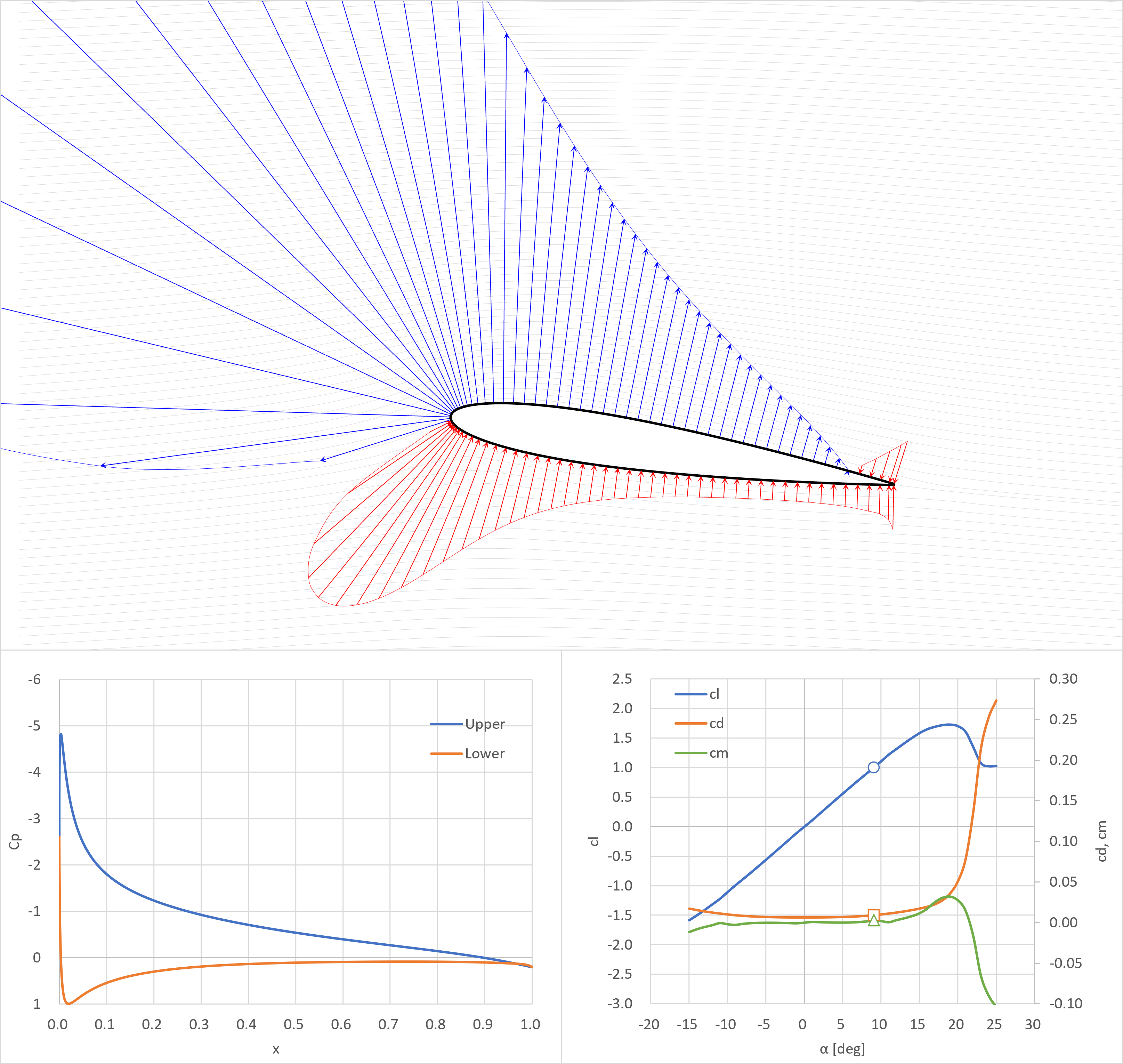
失速角
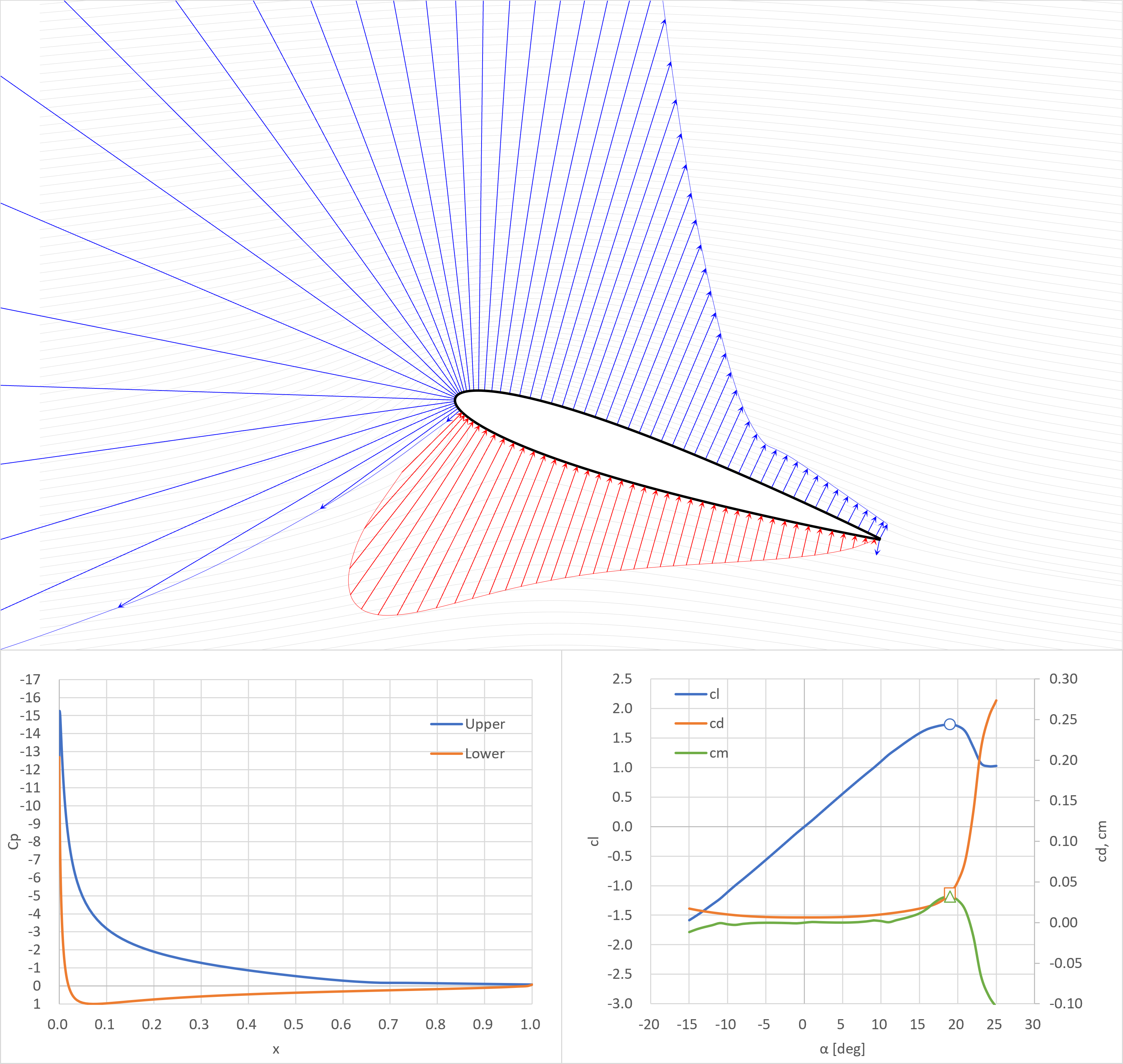
- 後縁のCp=0.078
失速角+4°
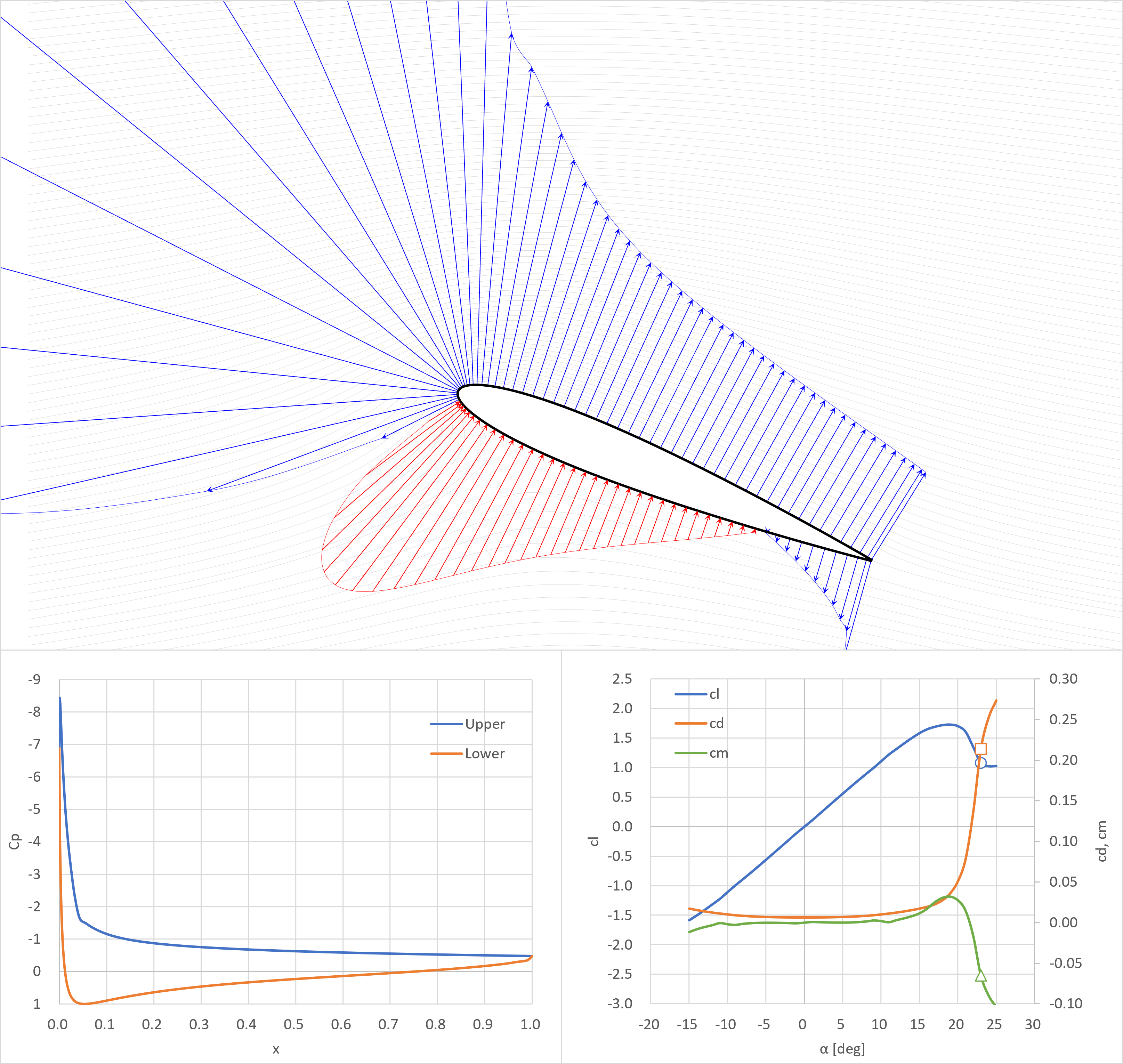
- 剥離領域が前縁付近まで到達
- 後縁のCp=-0.4717
- 剥離領域では圧力一定
- 翼表面の圧力は境界層の外側と同じ
キャンバー翼(NACA4412)
XFOIL解析条件
- Re=1E7
- Mach=0
- xtr=(0,0) ※前縁で強制遷移
ゼロ揚力角
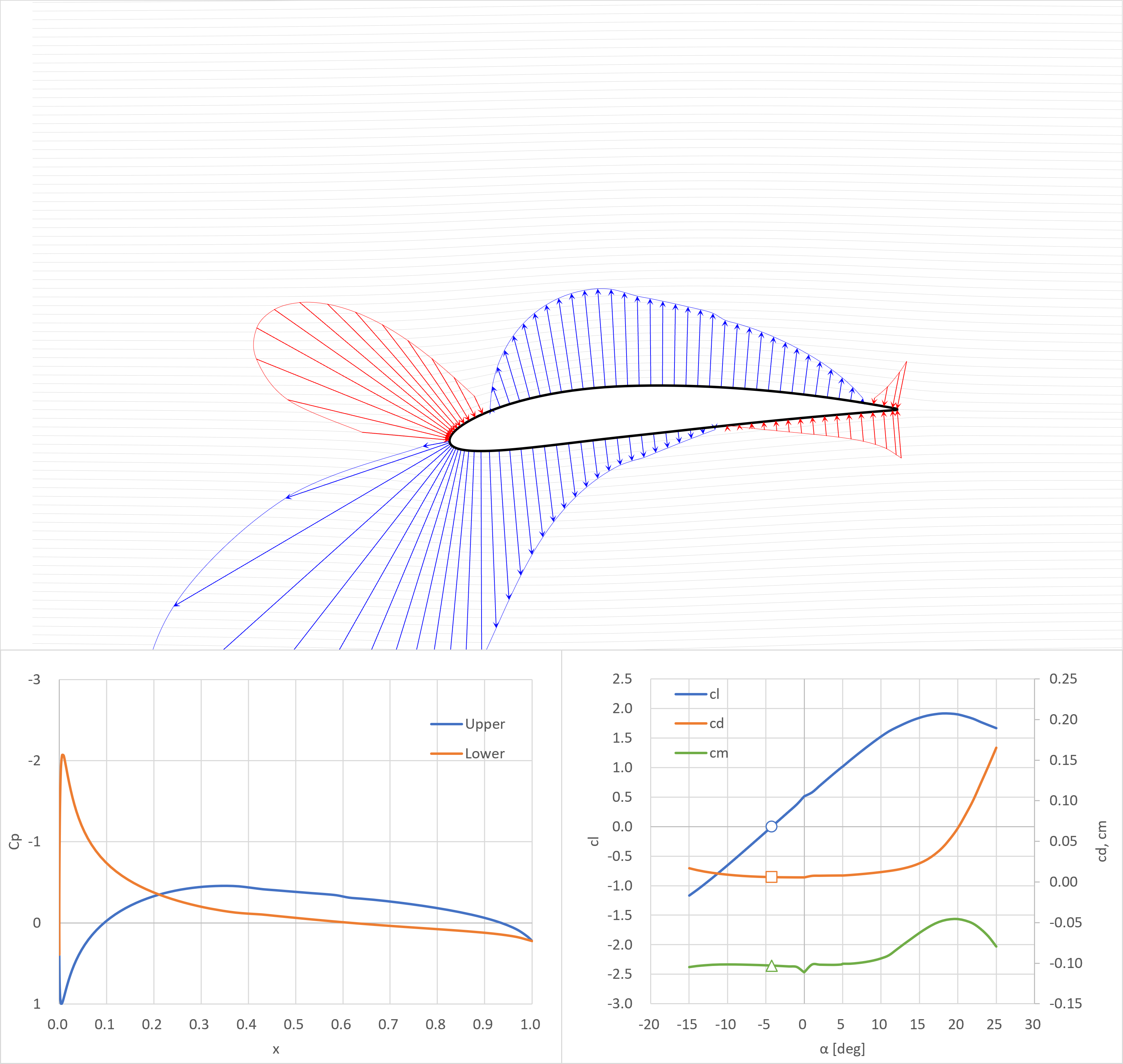
cl=0.5
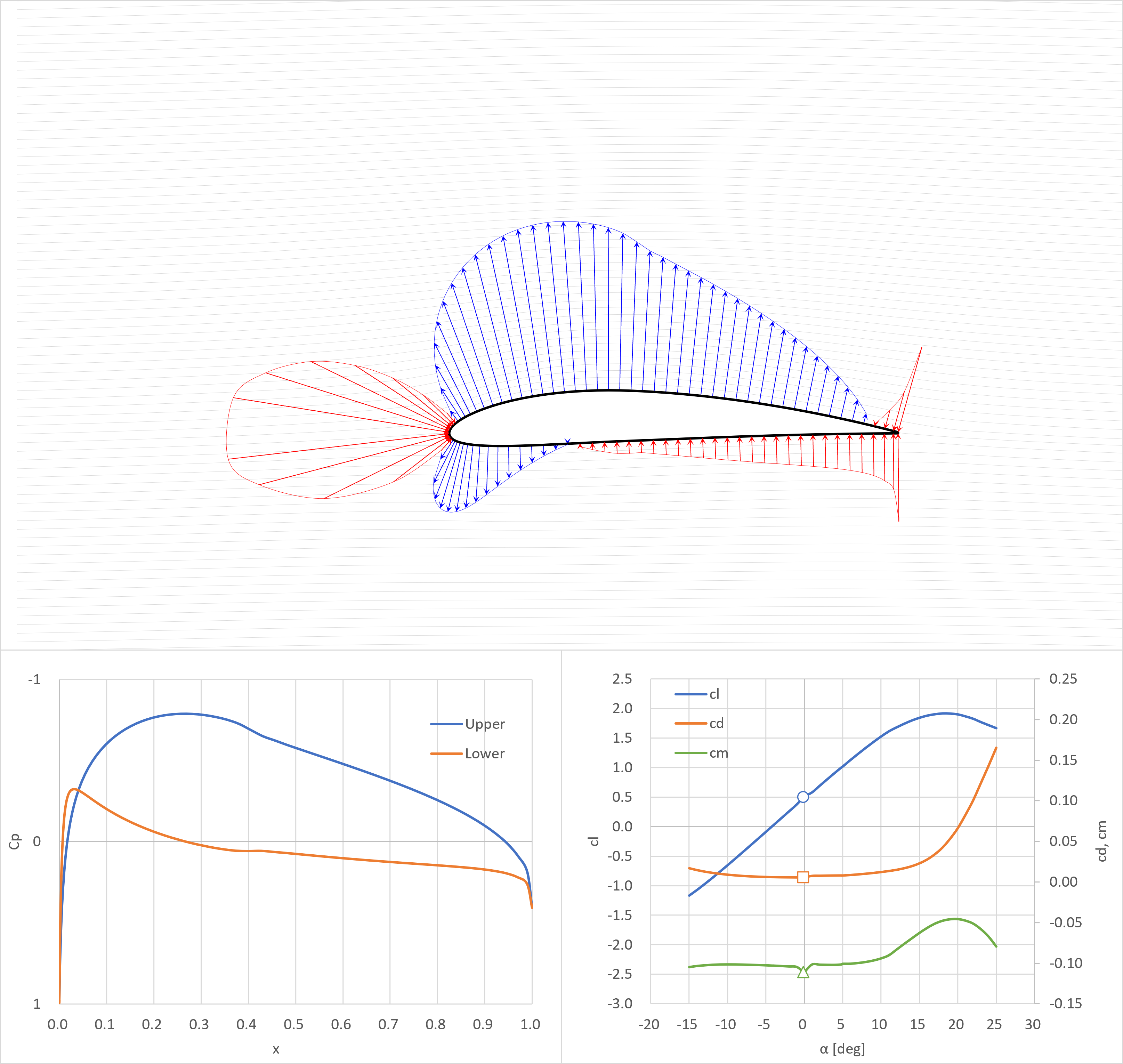
cl=1.0
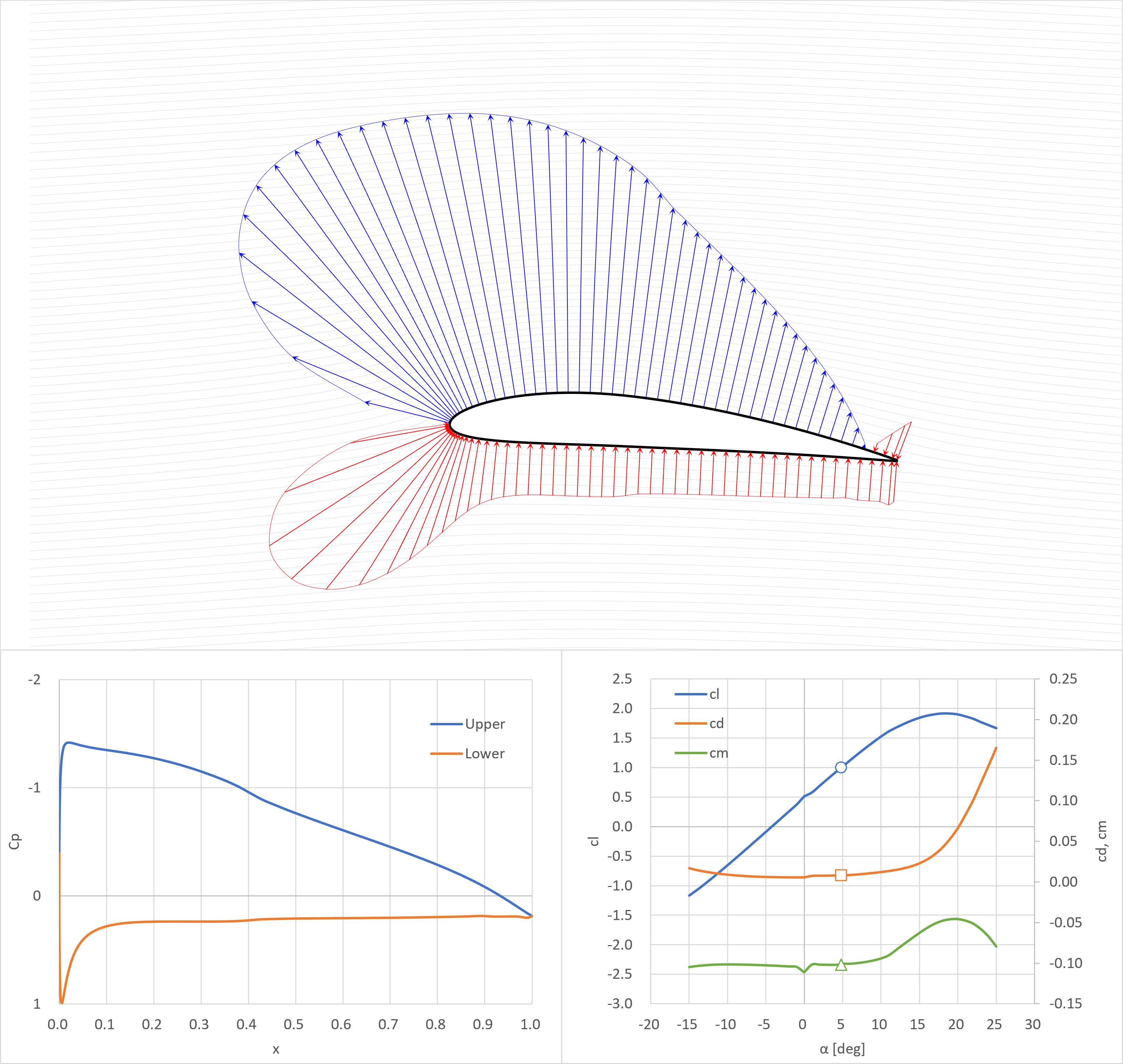
失速角
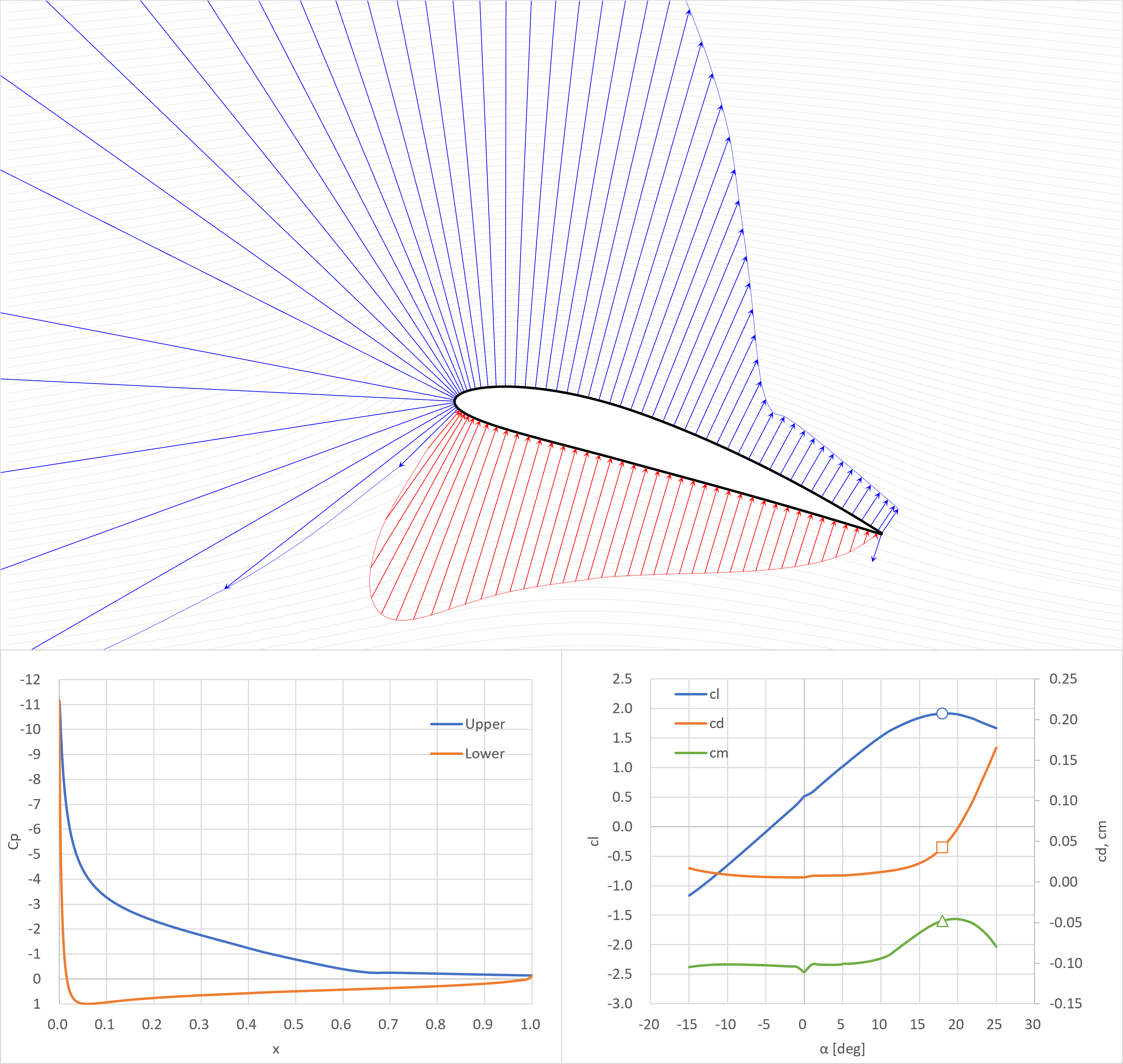
失速角+
反転キャンバー翼(NACA25112)
XFOIL解析条件
- Re=1E7
- Mach=0
- xtr=(0,0) ※前縁で強制遷移
ゼロ揚力角
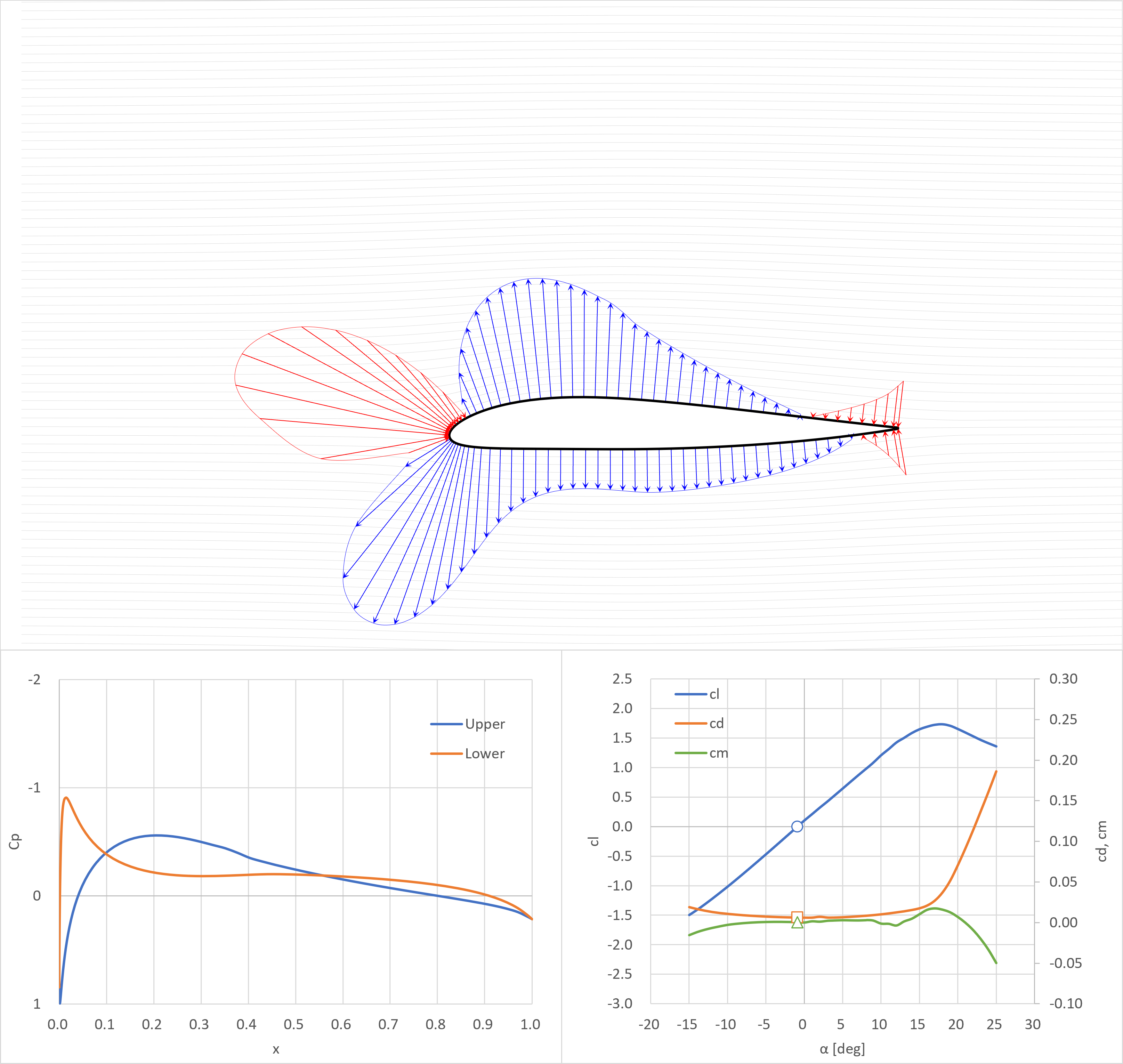
- 翼後縁付近で下面の圧力の方が上面よりも低くなっている(下向きの力を生じている)
cl=0.5
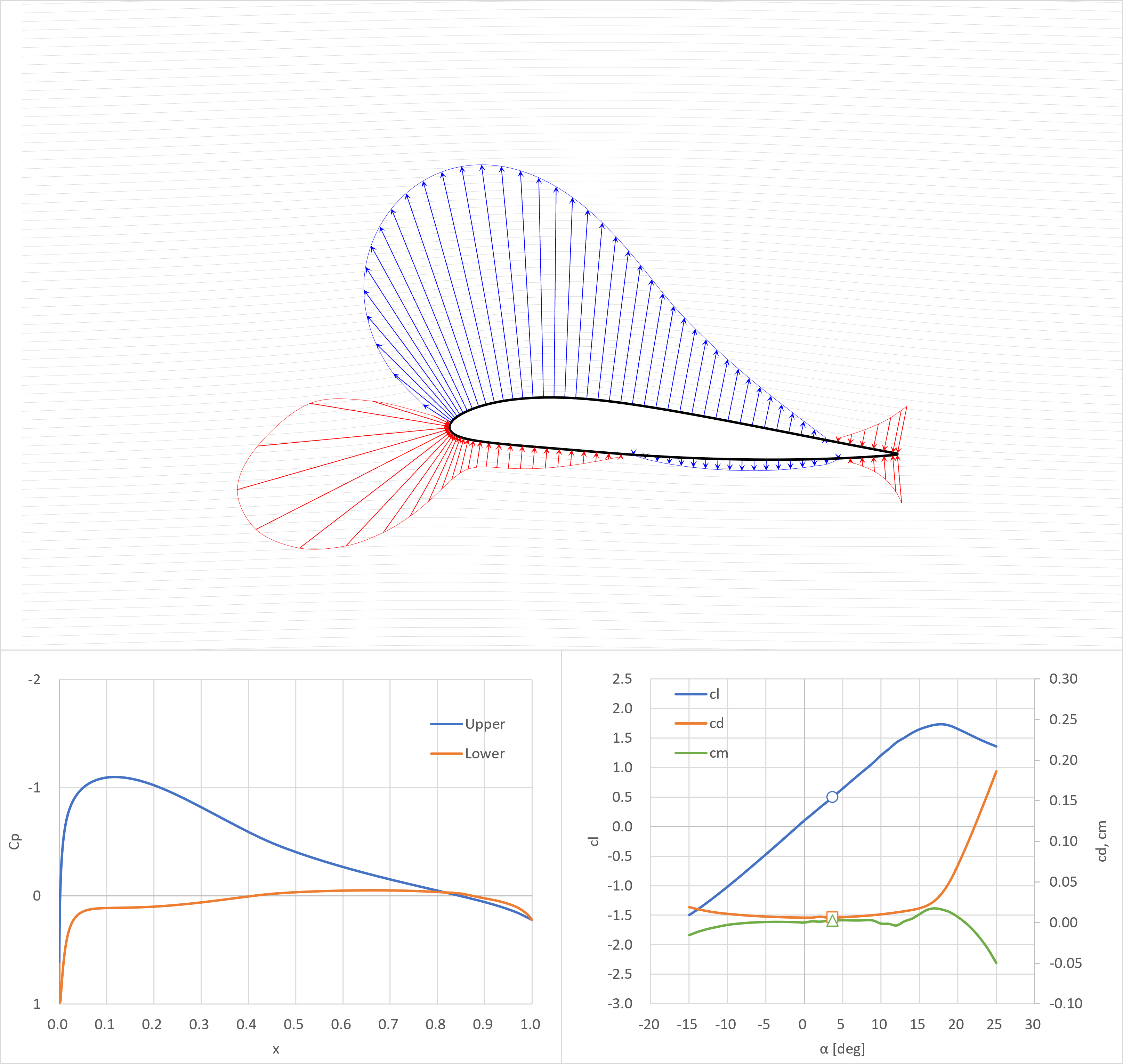
cl=1.0
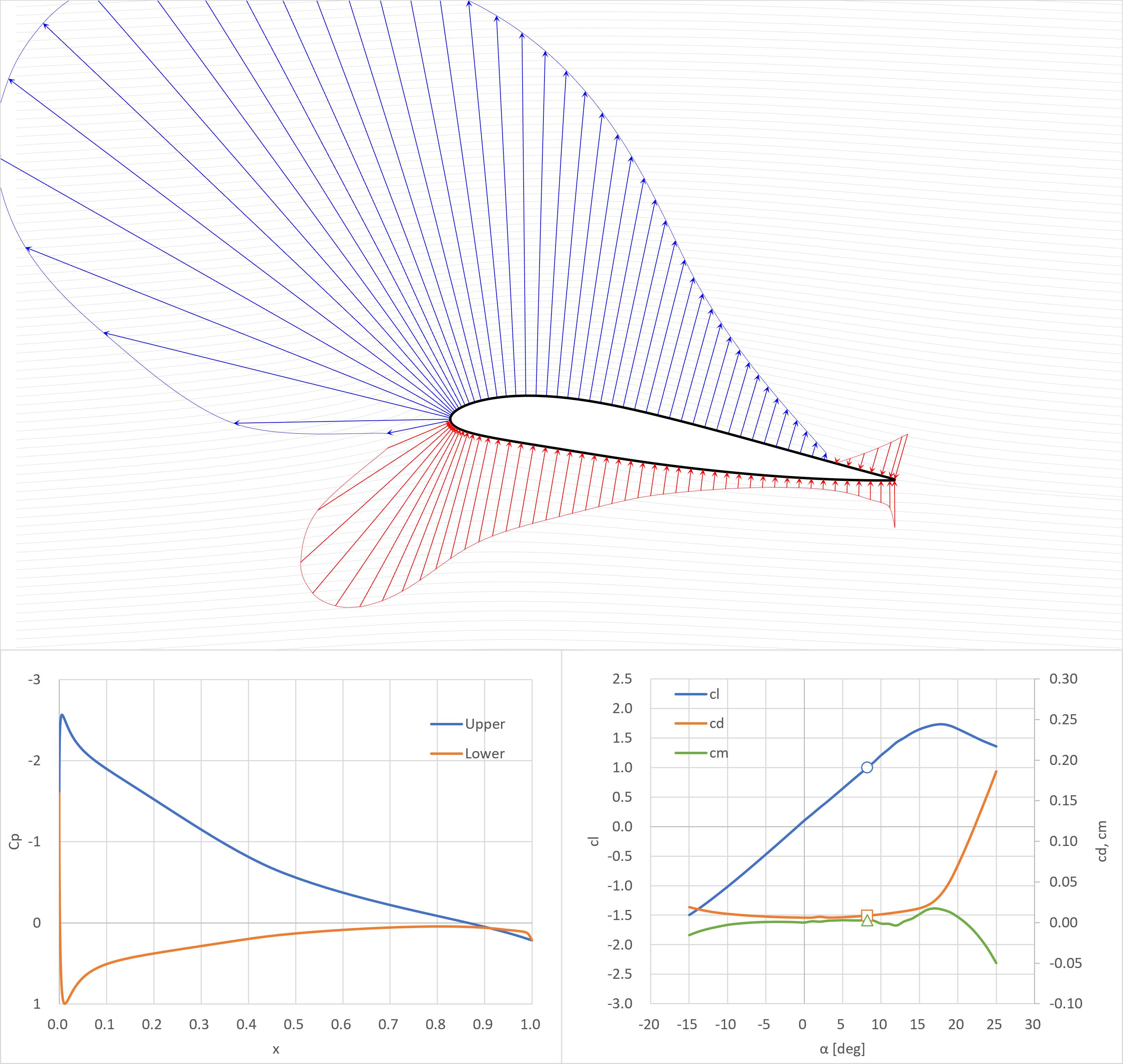
失速角
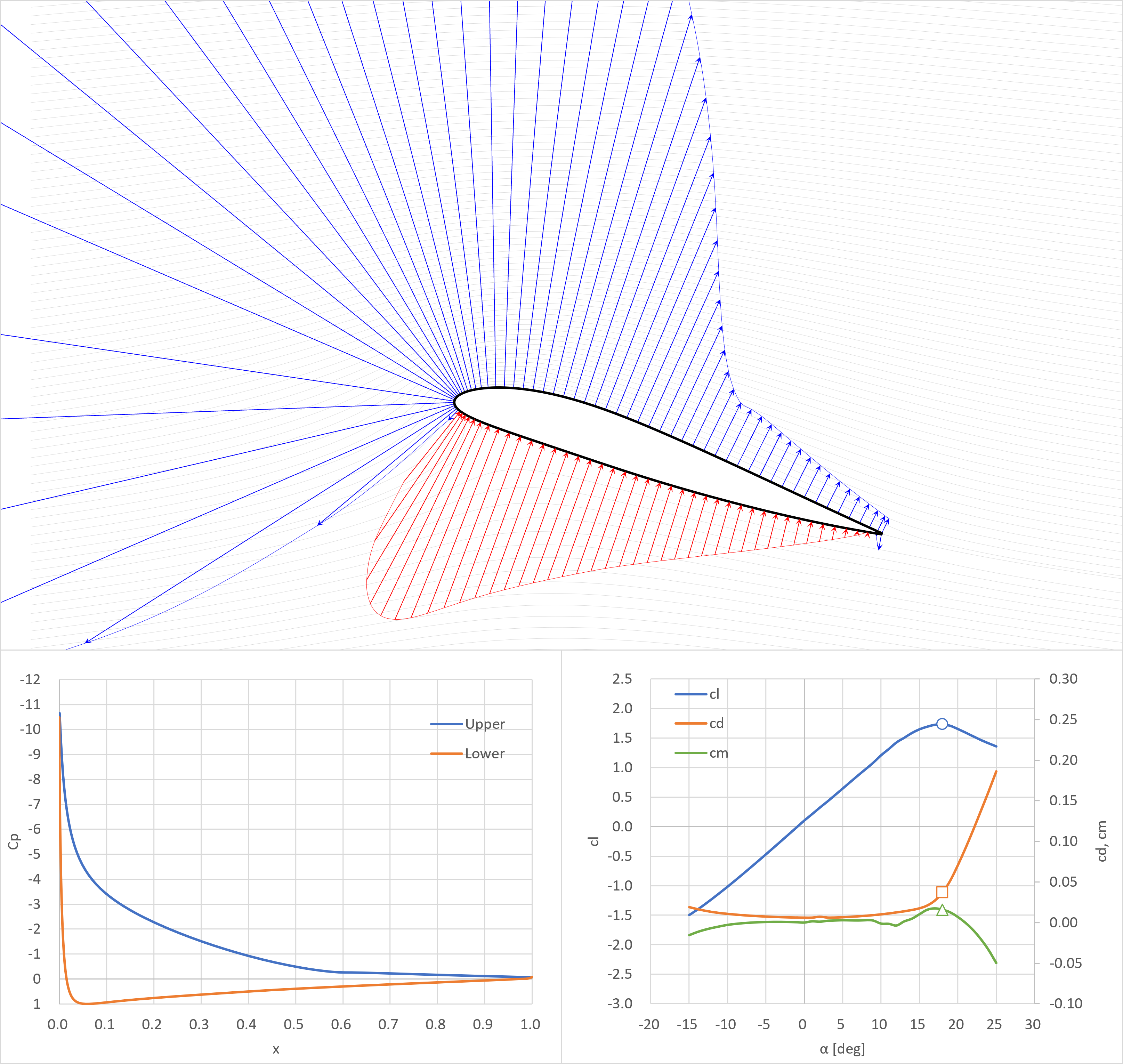
失速角+4°
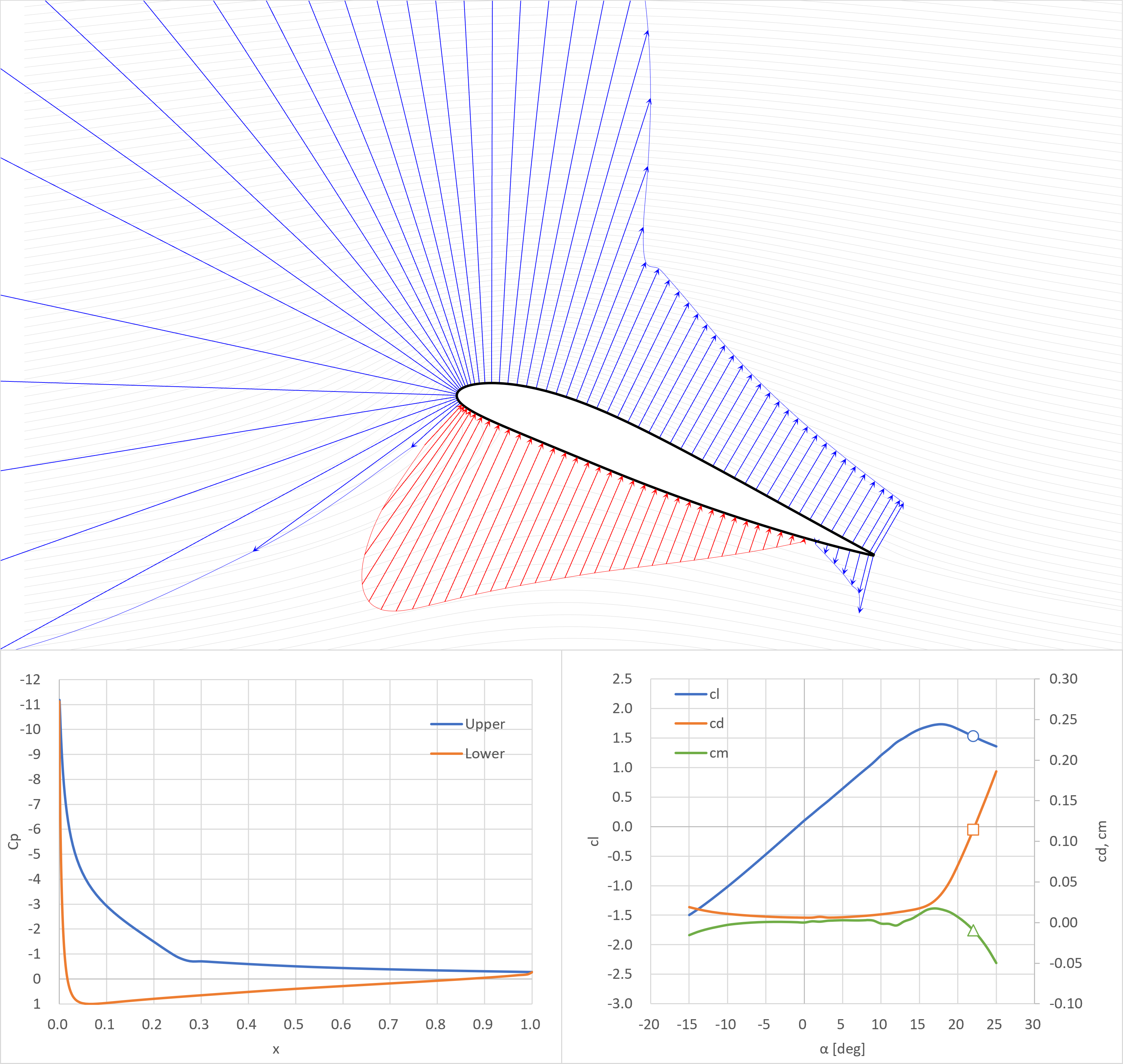
超臨界翼(SC(2)-0410)
XFOIL解析条件
- Re=1E7
- Mach=0
- xtr=(0,0) ※前縁で強制遷移
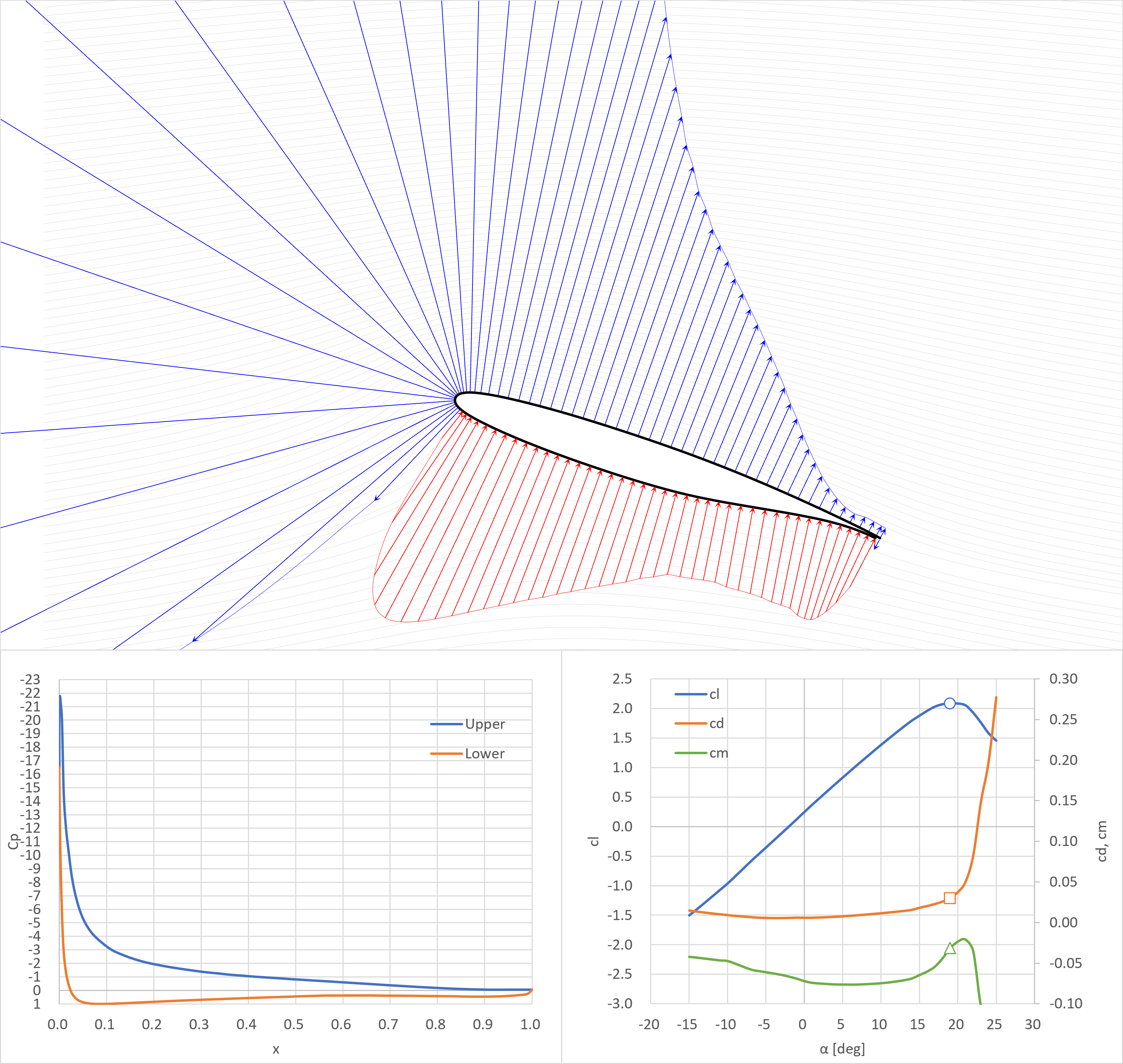
ゼロ揚力角
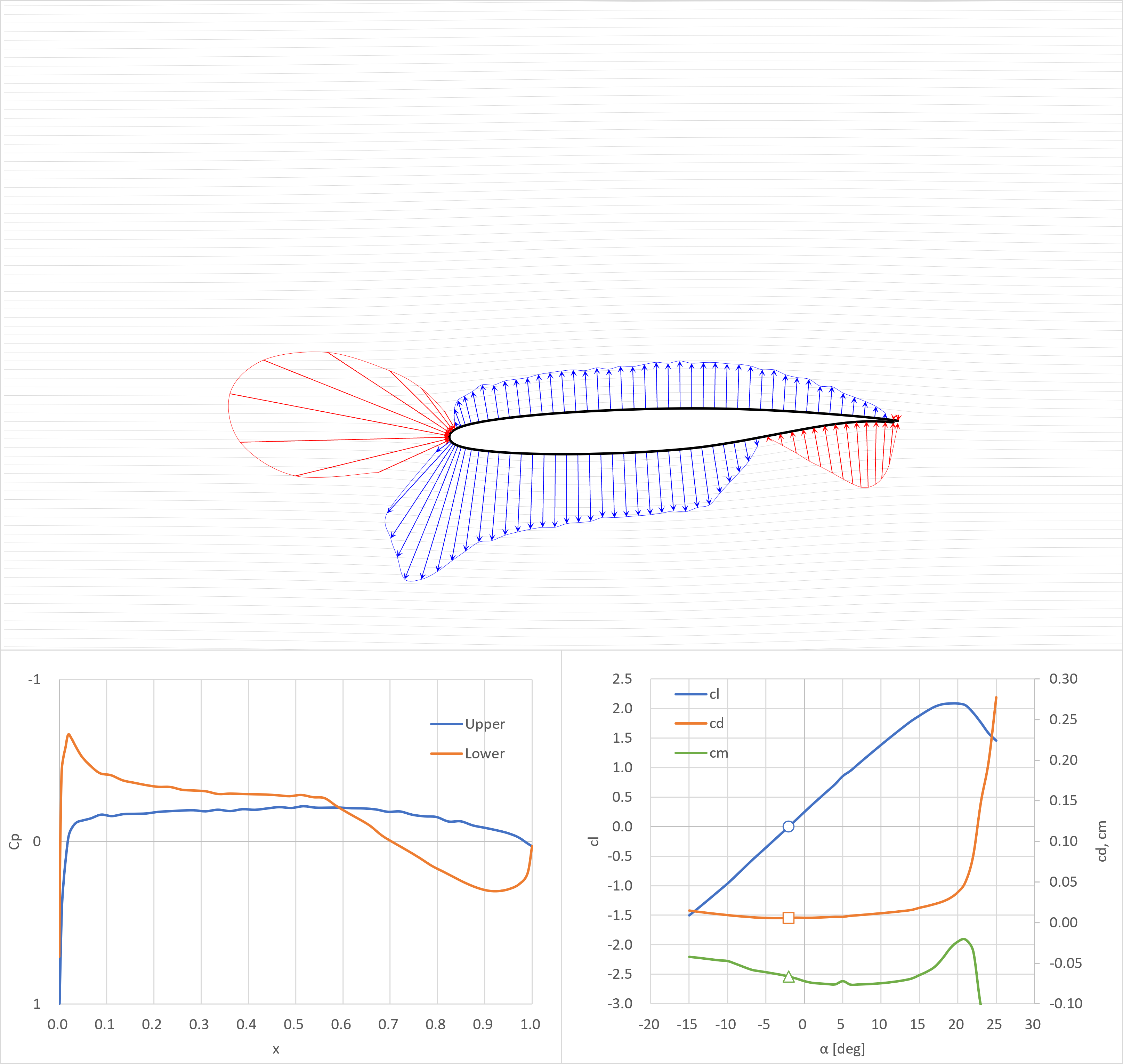
cl=0.5
- 翼上面では平らな圧力分布
- 翼後縁下面側で大きな揚力を生じている
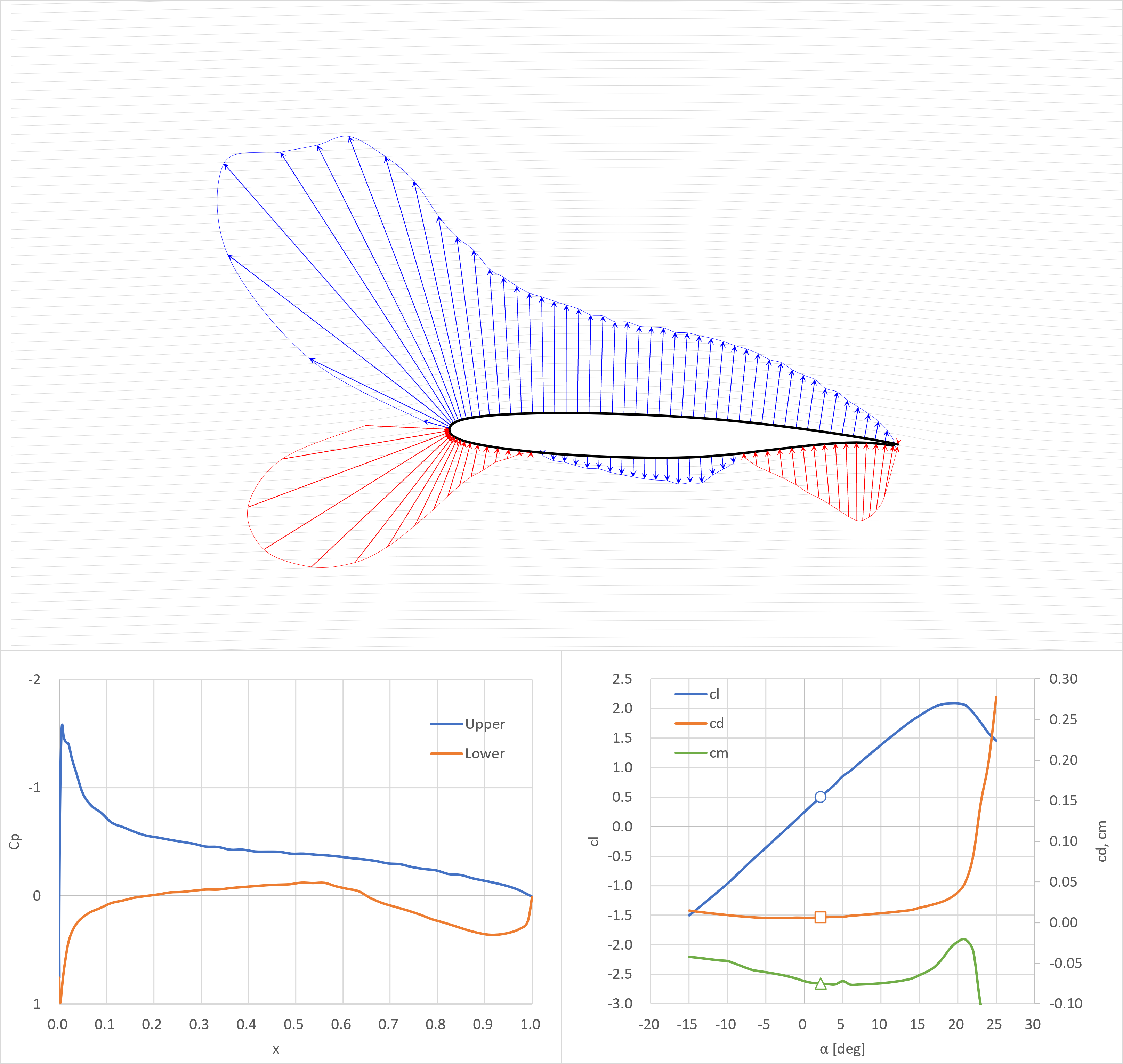
cl=1.0
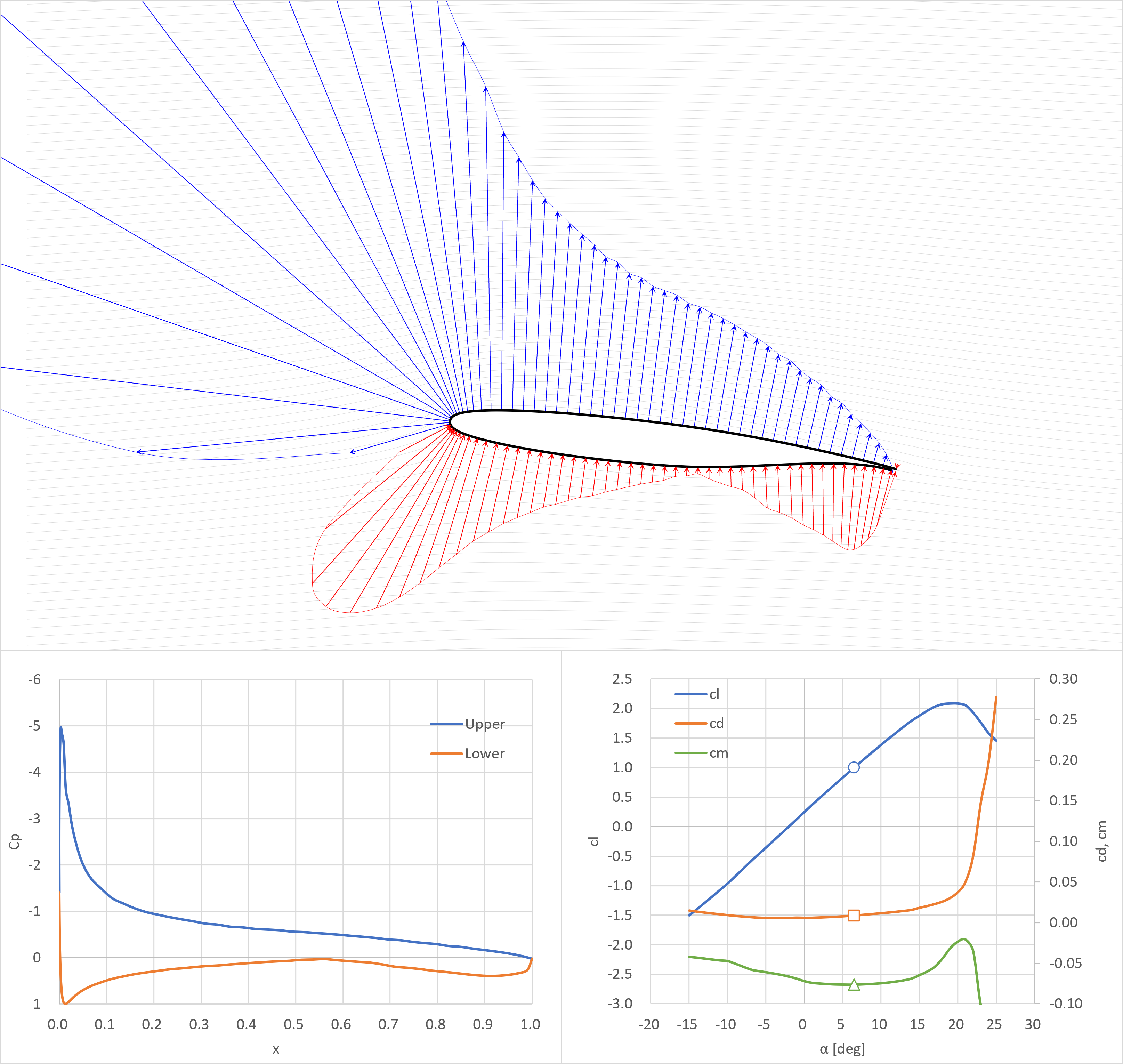
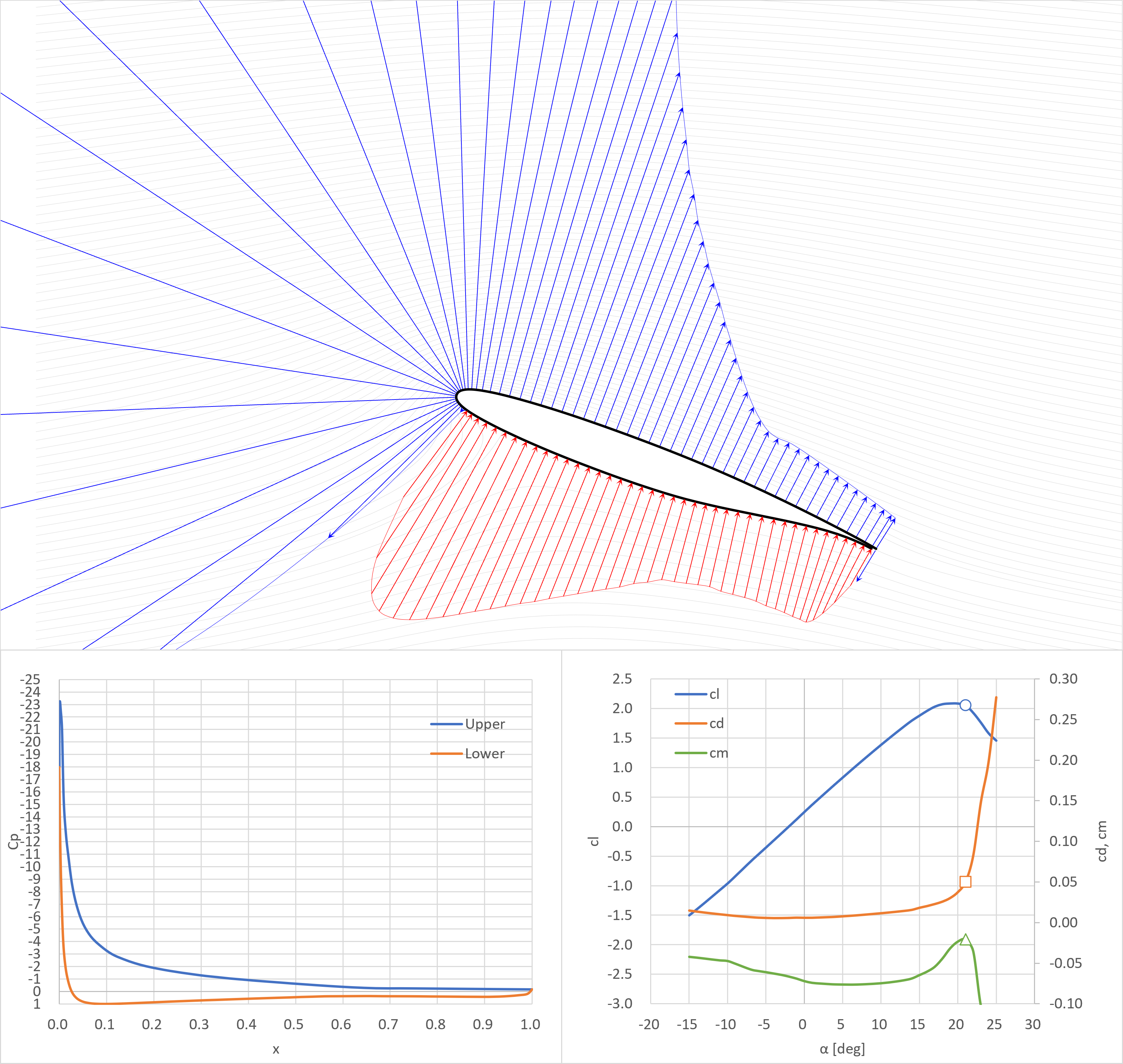
失速角
失速角+2°
おわりに
翼型の圧力分布を理解するために、いろいろな翼型の圧力分布を紹介した
↓圧力分布の表示に使ったExcelマクロはこれ
↓マクロはこれ
Const pi As Double = 3.14159265358979
Const rad As Double = pi / 180
Sub Main()
' 定数
Const U0 As Double = 1#
Const OutputFile_name As String = "Output.txt"
Const title As String = "Cm vs alpha"
' 変数
Dim z_foil() As Variant
Dim foil_name As String
Dim file_name As String
Dim alpha As Variant
Dim da As Double
Dim nodes As Long
Dim n As Long
' フォイルのサイズを確認し、z_foilを取得
With Sheets("dat")
dat = .Range(.Range("A2:B2"), .Range("A2:B2").End(xlDown))
End With
nodes = UBound(dat, 1) - 1
' Airfoilの読み込み
ReDim z_foil(1 To nodes + 1, 1 To 1) As Variant
For n = 1 To nodes + 1
x = dat(n, 1)
y = dat(n, 2)
z_foil(n, 1) = Application.Complex(x, y)
Next n
' 出力ファイルをリニューアル
With Sheets("BEM_gamma")
.Range(.Range(.Range("C6"), .Range("C6").End(xlDown)), .Range(.Range("C6"), .Range("C6").End(xlDown)).End(xlToRight)).ClearContents
.Range(.Range("D1:D3"), .Range("D1:D3").End(xlToRight)).ClearContents
End With
With Sheets("BEM")
.Range(.Range(.Range("C6"), .Range("C6").End(xlDown)), .Range(.Range("C6"), .Range("C6").End(xlDown)).End(xlToRight)).ClearContents
.Range(.Range("D2:D4"), .Range("D2:D4").End(xlToRight)).ClearContents
alpha = .Range(.Range("D1"), .Range("D1").End(xlToRight))
End With
' 処理ループ
For n = 1 To UBound(alpha, 2)
da = alpha(1, n)
Call Analize_foil(z_foil, U0, da, n - 1)
Next n
End Sub
Sub Analize_foil(z_foil() As Variant, U0 As Double, alpha As Double, cnt As Long)
'Application.ScreenUpdating = False
' 定数
Const kmax As Integer = 40 ' ストリームラインの数
Const xmin As Double = -0.5
Const xmax As Double = 1.5
Const ymin As Double = -0.5
Const ymax As Double = 0.5 ' グラフの範囲
Dim title As String ' タイトル
Dim U_inf As Variant ' 一様流
Dim z_qtr As Double '25%c
' 変数
Dim S1() As Variant
Dim S2() As Variant
Dim l() As Double
Dim z_ref() As Variant
Dim zWall As Variant
Dim Cp() As Double
Dim A() As Double
Dim B() As Double
Dim gamma() As Variant
Dim Cl As Double ' 揚力係数
Dim Cm As Double ' ピッチングモーメント係数
Dim i As Integer, j As Integer, k As Integer, n As Integer
nodes = UBound(z_foil, 1) - 1
With Application.WorksheetFunction
' 一様流の計算
U_inf = Application.Complex(U0 * Cos(alpha * rad), -U0 * Sin(alpha * rad))
z_qtr = Application.Complex(0.25, 0)
'*************************************************
' S1とS2の作成
ReDim S1(1 To nodes, 1 To nodes)
ReDim S2(1 To nodes, 1 To nodes)
ReDim l(1 To nodes)
ReDim z_ref(1 To nodes)
' Make l & z_ref
For i = 1 To nodes
l(i) = .ImAbs(.ImSub(z_foil(i + 1, 1), z_foil(i, 1)))
z_ref(i) = .ImDiv(.ImSum(z_foil(i, 1), z_foil(i + 1, 1)), 2)
Next i
' Make S1 & S2
For k = 1 To nodes
For j = 1 To nodes
S1(k, j) = .ImProduct(.ImDiv(Application.Complex(0, l(j)), .ImProduct(2 * pi, .ImSub(z_foil(j + 1, 1), z_foil(j, 1)))), .ImSum(-1, .ImProduct(.ImDiv(.ImSub(z_foil(j + 1, 1), z_ref(k)), .ImSub(z_foil(j + 1, 1), z_foil(j, 1))), .ImLn(.ImDiv(.ImSub(z_foil(j + 1, 1), z_ref(k)), .ImSub(z_foil(j, 1), z_ref(k)))))))
S2(k, j) = .ImProduct(.ImDiv(Application.Complex(0, l(j)), .ImProduct(2 * pi, .ImSub(z_foil(j + 1, 1), z_foil(j, 1)))), .ImSub(1, .ImProduct(.ImDiv(.ImSub(z_foil(j + 0, 1), z_ref(k)), .ImSub(z_foil(j + 1, 1), z_foil(j, 1))), .ImLn(.ImDiv(.ImSub(z_foil(j + 1, 1), z_ref(k)), .ImSub(z_foil(j, 1), z_ref(k)))))))
Next j
Next k
'*************************************************
' AとBの作成
ReDim A(1 To nodes + 1, 1 To nodes + 1)
ReDim B(1 To nodes + 1, 1 To 1)
ReDim z_n(1 To nodes) As Variant
' Make z_n
For i = 1 To nodes
z_n(i) = .ImDiv(.ImSub(z_foil(i + 1, 1), z_foil(i, 1)), Application.Complex(0, l(i)))
Next i
' Make A
For k = 1 To nodes + 1
For j = 1 To nodes + 1
If k < nodes + 1 Then
If j = 1 Then
A(k, j) = .ImReal(.ImProduct(S1(k, j), z_n(k)))
ElseIf j = nodes + 1 Then
A(k, j) = .ImReal(.ImProduct(S2(k, j - 1), z_n(k)))
Else
A(k, j) = .ImReal(.ImProduct(.ImSum(S2(k, j - 1), S1(k, j)), z_n(k)))
End If
Else
A(k, j) = 0
End If
Next j
Next k
For k = 1 To nodes
B(k, 1) = -.ImReal(.ImProduct(U_inf, z_n(k)))
Next k
' Kutta条件
A(nodes + 1, 1) = 1
A(nodes + 1, nodes + 1) = 1
B(nodes + 1, 1) = 0
'方程式を解く
'ReDim gamma(1 To nodes + 1)
gamma = .MMult(.MInverse(A), B)
' Cpの計算
ReDim Cp(1 To nodes + 1) As Double
For n = 1 To nodes
zWall = .ImSum(z_ref(n), .ImProduct(z_n(n), l(n), 0.00001))
uv = Make_uv(zWall, U_inf, z_foil, gamma)
u = .ImAbs(uv)
U0 = .ImAbs(U_inf)
Cp(n) = (1 - (u / U0) * (u / U0))
Next n
' Cl, Cmの計算
Cl = 0
Cm = 0
For n = 1 To nodes
theta = .ImArgument(.ImSub(z_foil(n + 1, 1), z_foil(n, 1)))
pn = Cp(n) * l(n) * Cos(theta)
pt = -Cp(n) * l(n) * Sin(theta)
x = .ImReal(.ImSub(z_ref(n), z_qtr))
y = .Imaginary(.ImSub(z_ref(n), z_qtr))
Cl = Cl + pn * Cos(rad * alpha) - pt * Sin(rad * alpha)
Cm = Cm - pn * x + pt * y
Next n
End With
With Sheets("BEM")
'.Cells(1, 4 + cnt) = alpha
.Cells(2, 4 + cnt) = Cl
.Cells(3, 4 + cnt) = 0
.Cells(4, 4 + cnt) = Cm
.Range(.Cells(6, 3), .Cells(6 + nodes - 1, 3)) = WorksheetFunction.Transpose(z_ref)
.Range(.Cells(6, 4 + cnt), .Cells(6 + nodes - 1, 4 + cnt)) = WorksheetFunction.Transpose(Cp)
End With
With Sheets("BEM_gamma")
'.Cells(1, 4 + cnt) = alpha
.Cells(2, 4 + cnt) = Cl
.Cells(3, 4 + cnt) = 0
.Cells(3, 4 + cnt) = Cm
.Range(.Cells(6, 3), .Cells(6 + nodes, 3)) = z_foil
.Range(.Cells(6, 4 + cnt), .Cells(6 + nodes, 4 + cnt)) = gamma
End With
'Application.ScreenUpdating = True
End Sub
Function Make_uv(z_ref As Variant, U_inf As Variant, z_foil As Variant, gamma As Variant) As Variant
Dim S1_uv() As Variant
Dim S2_uv() As Variant
Dim l() As Variant
Dim k As Integer
nodes = UBound(z_foil, 1) - 1
ReDim S1_uv(1 To nodes) As Variant
ReDim S2_uv(1 To nodes) As Variant
ReDim l(1 To nodes)
With Application.WorksheetFunction
' Make l & z_ref
For i = 1 To nodes
l(i) = .ImAbs(.ImSub(z_foil(i + 1, 1), z_foil(i, 1)))
Next i
' Make S1 & S2
For k = 1 To nodes
S1_uv(k) = .ImProduct(.ImDiv(Application.Complex(0, l(k)), .ImProduct(2 * pi, .ImSub(z_foil(k + 1, 1), z_foil(k, 1)))), .ImSum(-1, .ImProduct(.ImDiv(.ImSub(z_foil(k + 1, 1), z_ref), .ImSub(z_foil(k + 1, 1), z_foil(k, 1))), .ImLn(.ImDiv(.ImSub(z_foil(k + 1, 1), z_ref), .ImSub(z_foil(k, 1), z_ref))))))
S2_uv(k) = .ImProduct(.ImDiv(Application.Complex(0, l(k)), .ImProduct(2 * pi, .ImSub(z_foil(k + 1, 1), z_foil(k, 1)))), .ImSub(1, .ImProduct(.ImDiv(.ImSub(z_foil(k + 0, 1), z_ref), .ImSub(z_foil(k + 1, 1), z_foil(k, 1))), .ImLn(.ImDiv(.ImSub(z_foil(k + 1, 1), z_ref), .ImSub(z_foil(k, 1), z_ref))))))
Next k
' eq.(4.42)
uv = .ImSum(U_inf, .ImProduct(S1_uv(1), gamma(1, 1)), .ImProduct(S2_uv(nodes), gamma(nodes + 1, 1)))
For k = 2 To nodes
uv = .ImSum(uv, .ImProduct(.ImSum(S1_uv(k), S2_uv(k - 1)), gamma(k, 1)))
Next k
End With
Make_uv = uv
End Function
Sub plotStreamline()
' 定数
Const U0 As Double = 1
Const dy As Double = 0.02
Const xmin As Double = -1
Const xmax As Double = 2.5
Const ymin As Double = -0.7
Const ymax As Double = 1 ' グラフの範囲
Dim U_inf As Variant ' 一様流
Dim z_qtr As Double '25%c
Dim sht As Worksheet
Dim l() As Variant
Dim z_n() As Variant
Dim z_foil As Variant
Dim z_ref As Variant
Dim zStart As Variant
Dim zStag As Variant
Dim Cp As Variant
Dim x As Variant
Dim gamma As Variant
Dim alpha As Double
Dim nStag As Long
Dim xy As Variant
Set sht = Worksheets("Streamline")
U_inf = Application.Complex(U0, 0) 'Application.Complex(U0 * Cos(alpha * rad), -U0 * Sin(alpha * rad))
z_qtr = Application.Complex(0.25, 0)
nCol = 5
With Sheets("BEM_gamma")
z_foil = .Range(.Cells(6, 3), .Cells(6, 3).End(xlDown))
gamma = .Range(.Cells(6, 3 + nCol), .Cells(6, 3 + nCol).End(xlDown))
'x = .Range(.Cells(6, 1), .Cells(6, 1).End(xlDown))
End With
With Sheets("BEM")
Cp = .Range(.Cells(6, 3 + nCol), .Cells(6, 3 + nCol).End(xlDown))
alpha = .Cells(1, 3 + nCol)
End With
sht.Range("D6:E99999").ClearContents
With WorksheetFunction
nodes = UBound(z_foil, 1) - 1
ReDim l(1 To nodes)
ReDim z_n(1 To nodes)
ReDim z_ref(1 To nodes)
For i = 1 To UBound(z_foil, 1)
z_foil(i, 1) = .ImSum(.ImProduct(.ImSub(z_foil(i, 1), z_qtr), .Complex(Cos(-rad * alpha), Sin(-rad * alpha))), z_qtr)
Next i
' Make l & z_ref
For i = 1 To nodes
l(i) = .ImAbs(.ImSub(z_foil(i + 1, 1), z_foil(i, 1)))
z_ref(i) = .ImDiv(.ImSum(z_foil(i, 1), z_foil(i + 1, 1)), 2)
z_n(i) = .ImDiv(.ImSub(z_foil(i + 1, 1), z_foil(i, 1)), Application.Complex(0, l(i)))
Next i
sht.Cells(1, 4 + cnt) = alpha
sht.Range(sht.Cells(6, 3), sht.Cells(6 + nodes, 3)) = z_foil
nRow = 0
nStag = .Match(.Max(Cp), Cp, 0)
zStag = .ImSum(z_ref(nStag), .ImProduct(z_n(nStag), l(nStag), 0.01))
zStart = zStag
xy = streamline(U_inf, zStart, z_foil, gamma, xmin, zStag)
sht.Range(sht.Cells(6 + nRow, 4), sht.Cells(6 + nRow + UBound(xy, 1) - 1, 5)) = xy
nRow = nRow + UBound(xy, 1) + 1
x = xy(UBound(xy, 1), 1)
y = xy(UBound(xy, 1), 2)
zStart = .ImDiv(.ImSum(z_foil(1, 1), z_foil(nodes + 1, 1)), 2)
xy = streamline(U_inf, zStart, z_foil, gamma, xmax, zStart)
sht.Range(sht.Cells(6 + nRow, 4), sht.Cells(6 + nRow + UBound(xy, 1) - 1, 5)) = xy
nRow = nRow + UBound(xy, 1) + 1
n = 0
Do While y > ymin
y = y - dy
zStart = .Complex(x, y)
xy = streamline(U_inf, zStart, z_foil, gamma, xmax, zStag)
sht.Range(sht.Cells(6 + nRow, 4), sht.Cells(6 + nRow + UBound(xy, 1) - 1, 5)) = xy
nRow = nRow + UBound(xy, 1) + 1
n = n + 1
Loop
y = y + dy * (n + 0)
Do While y < ymax
y = y + dy
zStart = .Complex(x, y)
xy = streamline(U_inf, zStart, z_foil, gamma, xmax, zStag)
sht.Range(sht.Cells(6 + nRow, 4), sht.Cells(6 + nRow + UBound(xy, 1) - 1, 5)) = xy
nRow = nRow + UBound(xy, 1) + 1
n = n + 1
Loop
End With
End Sub
Function streamline(U_inf As Variant, zStart As Variant, z_foil As Variant, gamma As Variant, xlimit As Double, zStag As Variant) As Variant
Const dt0 As Double = 0.1
Const dtheta_max As Double = 100000
Dim uv As Variant
Dim z_ref As Variant
Dim x, y As Double
Dim u, v As Double
Dim dt As Double
Dim theta, theta0, dtheta As Double
Dim tmp(1 To 9999, 1 To 2) As Variant
Dim pm As Double
With WorksheetFunction
pm = (xlimit - .ImReal(zStart)) / Abs(xlimit - .ImReal(zStart))
z_ref = zStart
x = .ImReal(z_ref)
y = .Imaginary(z_ref)
n = 0
dt = dt0
Do While (xlimit - x) / pm > 0
n = n + 1
tmp(n, 1) = x
tmp(n, 2) = y
uv = Make_uv(z_ref, U_inf, z_foil, gamma)
u = .ImReal(uv)
v = -.Imaginary(uv)
dt = dt0 * (0.01 + (.Min(.ImAbs(.ImSub(z_ref, zStag)), 1) / .ImAbs(uv)) ^ 2)
x = x + u * dt * pm
y = y + v * dt * pm
z_ref = .Complex(x, y)
Loop
End With
ReDim xy(1 To n, 1 To 2)
For i = 1 To n
xy(i, 1) = tmp(i, 1)
xy(i, 2) = tmp(i, 2)
Next i
streamline = xy
End Function
コメント