最大応力説を使って積層板の強度を計算してみる
目的とフローチャート
今回の目的は,最大応力説を使って積層板の強度を計算してみることである
以下の資料を参考にする
複合材料の力学序説 古今書院 以下,(序)
入門複合材料の力学 培風館 以下,(入)
どちらかというと(入)のほうが破損則については詳しい
前回の記事で作った設計シートに付け加える形で進めていくので,この記事を読む前に目を通しておいてほしい
ここで扱う破損則について,注意すべき点を引用する
問題点1:破壊がすべて応力だけを基準として議論をされている.しかし,何層にも積み上げられた実際の複合材料積層板では,層間の干渉により,必ずしも一方向材の強度だけでは議論ができない(この点については,後でも述べる)
入門複合材料の力学 培風館 p.115
問題点2:実際の複合材料積層板の破壊現象は複雑で,必ずしも面内破壊だけではなく,層間剝離や座屈といった面外の破壊モードも考慮しなくてはいけない
使用する式は以下のとおりである(数式は必ず参考文献を自分で確認すること.誤字脱字注意!)
積層板の合力とひずみの関係式 (序)p.126
\begin{eqnarray}
\left[ \begin{array}{c}
N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy}
\end{array} \right] =
\left[ \begin{array}{cccccc}
A_{11} & A_{12} & A_{16} & B_{11} & B_{12} & B_{16} \\
A_{12} & A_{22} & A_{26} & B_{12} & B_{22} & B_{26} \\
A_{16} & A_{26} & A_{66} & B_{16} & B_{26} & B_{66} \\
B_{11} & B_{12} & B_{16} & D_{11} & D_{12} & D_{16} \\
B_{12} & B_{22} & B_{26} & D_{12} & D_{22} & D_{26} \\
B_{16} & B_{26} & B_{66} & D_{16} & D_{26} & D_{66} \\
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x^0 \\
\varepsilon_y^0 \\
\gamma_{xy}^0 \\
\chi_x^0 \\
\chi_y^0 \\
\chi_{xy}^0 \\
\end{array} \right]
\tag{6.9}
\end{eqnarray}
中央面からzだけ離れた任意の位置のラミナのフックの法則 (序)p.125
\begin{eqnarray}
\left[ \begin{array}{c}
\sigma_x \\
\sigma_y \\
\tau_{xy}
\end{array} \right] =
\left[ \begin{array}{ccc}
\overline{Q_{11}} & \overline{Q_{12}} & \overline{Q_{16}} \\
\overline{Q_{12}}& \overline{Q_{22}}& \overline{Q_{26}} \\
\overline{Q_{16}}& \overline{Q_{26}}& \overline{Q_{66}}
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x^0+z\chi_x \\
\varepsilon_y^0+z\chi_y \\
\gamma_{xy}^0+z\chi_{xy} \end{array} \right]
\tag{6.5}
\end{eqnarray}
最大応力説の破断の条件式 (C1)
\begin{eqnarray}
F_{L_c}<\sigma_{L}&<&F_{L_t} \\
F_{T_c}<\sigma_{T}&<&F_{T_t} \\
\tau_{LT}&<&F_{LT} \\
\tag{C1}
\end{eqnarray}
積層板の最弱層破壊の手順は以下の通り
①積層板にはたらく合力を求める(入力する)
②式(6.9)で積層板のひずみを求める
③式(6.5)で各層にはたらく応力を求める
④式(C1)で破断するかどうかを調べる
フローチャートを以下に示す
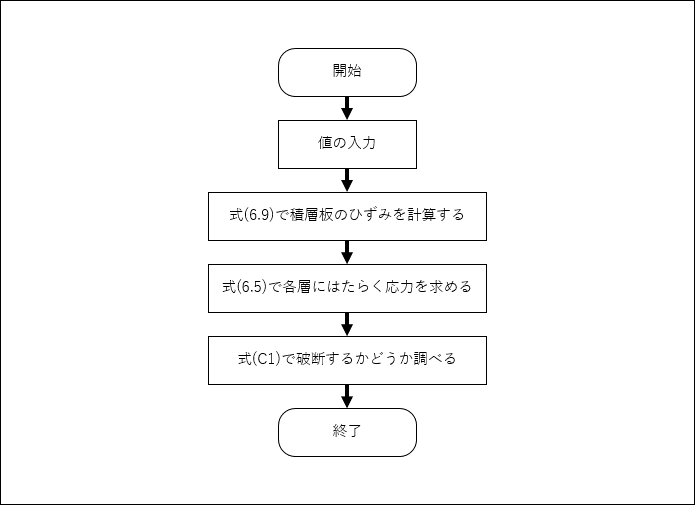
テンプレートファイルのダウンロード
エクセルの数式などの参考になるようにテンプレートファイルを添付しておく
エクセルシートの解説
それでは実際に解説していく
値の入力
セルD27~D32に積層板にはたらく合力,合モーメントを入力する
ここで合力,合モーメントは(序)p.126で次のように定義される
\begin{eqnarray}
(N_{x},N_{y},N_{xy}) &=& \sum_{k=1}^n \int_{z_{k-1}}^{z_{k}} (\sigma_{x}, \sigma_{y},\tau_{xy})dz
\tag{6.6}
\end{eqnarray}
\begin{eqnarray}
(M_{x},M_{y},M_{xy}) &=& \sum_{k=1}^n \int_{z_{k-1}}^{z_{k}} (\sigma_{x}z, \sigma_{y}z,\tau_{xy}z)dz
\tag{6.7}
\end{eqnarray}
定義式からはわかりづらいが,要は単位幅あたりにはたらく力,モーメントである
例えば断面が幅\( b \),厚さ\( t\)の積層板に\( \sigma_{x} \)の応力がはたらくとすると,合力\( N_{x} \)は次のようになる
\begin{eqnarray}
N_{x}=\frac{\sigma_{x}bc}{b}=\sigma_{x}c
\end{eqnarray}
ここではとりあえず\( N_{x}=1'200'000 \) [N/m]を入力しておく
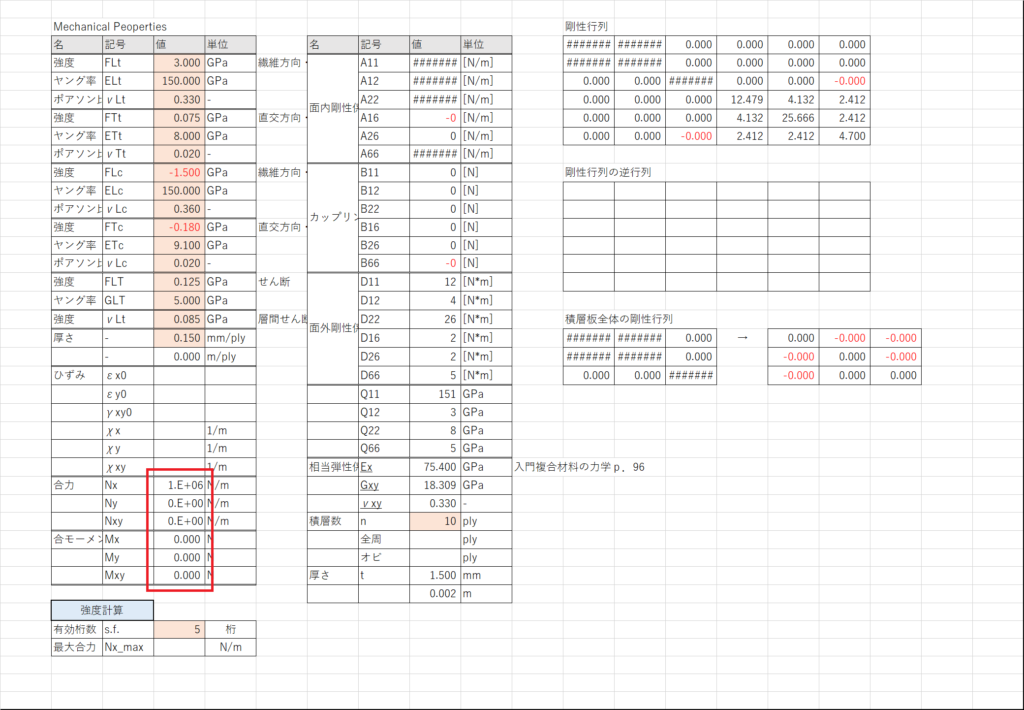
式(6.9)で積層板のひずみを計算する
式(6.9)で積層板のひずみを計算する
\begin{eqnarray}
\left[ \begin{array}{c}
N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy}
\end{array} \right] =
\left[ \begin{array}{cccccc}
A_{11} & A_{12} & A_{16} & B_{11} & B_{12} & B_{16} \\
A_{12} & A_{22} & A_{26} & B_{12} & B_{22} & B_{26} \\
A_{16} & A_{26} & A_{66} & B_{16} & B_{26} & B_{66} \\
B_{11} & B_{12} & B_{16} & D_{11} & D_{12} & D_{16} \\
B_{12} & B_{22} & B_{26} & D_{12} & D_{22} & D_{26} \\
B_{16} & B_{26} & B_{66} & D_{16} & D_{26} & D_{66} \\
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x^0 \\
\varepsilon_y^0 \\
\gamma_{xy}^0 \\
\chi_x^0 \\
\chi_y^0 \\
\chi_{xy}^0 \\
\end{array} \right]
\tag{6.9}
\end{eqnarray}
逆行列の計算にはMINVERSE関数,行列の掛け算にはMMULT関数を使う
セルL11~Q16でセルL3~Q8の逆行列を計算する
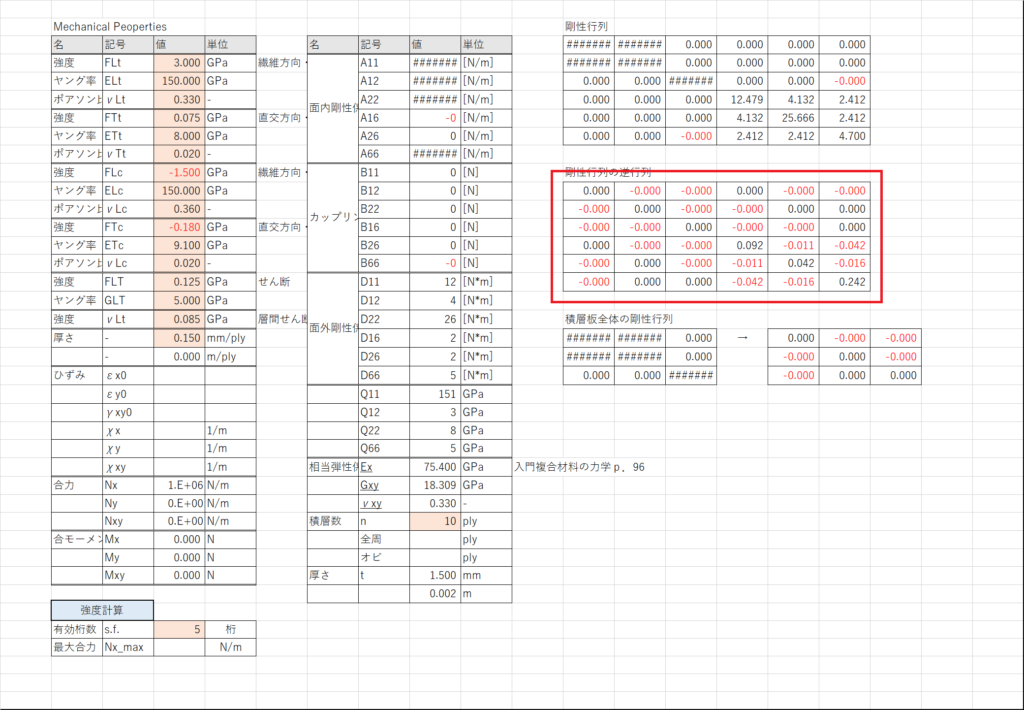
セルD21~D26で積層板のひずみを計算する
セルD21~D26を選択してから「F2」キーで「=MMULT(L11:Q16,D27:D32)」と入力し,「Ctrl+Shift+Enter」で入力を確定する
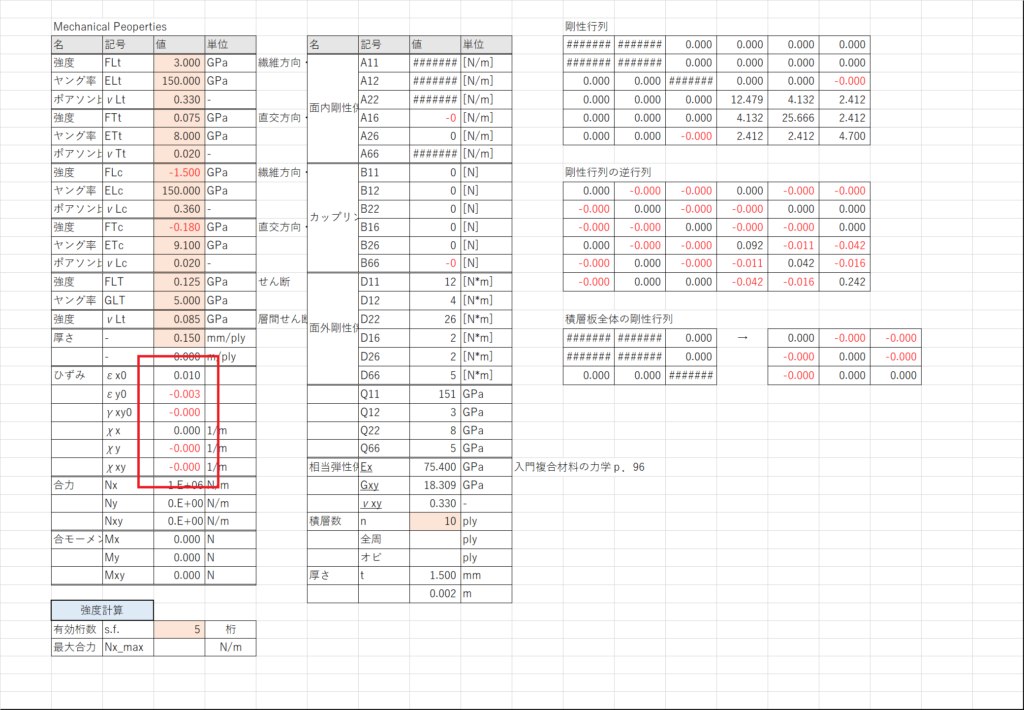
式(6.5)で各層にはたらく応力を求める
式(6.5)で各層にはたらく応力を求める
\begin{eqnarray}
\left[ \begin{array}{c}
\sigma_x \\
\sigma_y \\
\tau_{xy}
\end{array} \right] =
\left[ \begin{array}{ccc}
\overline{Q_{11}} & \overline{Q_{12}} & \overline{Q_{16}} \\
\overline{Q_{12}}& \overline{Q_{22}}& \overline{Q_{26}} \\
\overline{Q_{16}}& \overline{Q_{26}}& \overline{Q_{66}}
\end{array} \right]
\left[ \begin{array}{c}
\varepsilon_x^0+z\chi_x \\
\varepsilon_y^0+z\chi_y \\
\gamma_{xy}^0+z\chi_{xy} \end{array} \right]
\tag{6.5}
\end{eqnarray}
セルX17~X19~で式(6.5)を計算する
いまいちSUMPRODUCT関数が使いにくいので掛け算と足し算で頑張ろう
中央面からの距離\( z\) は\( z_{k}\)と\( z_{k-1}\)の平均値を使う
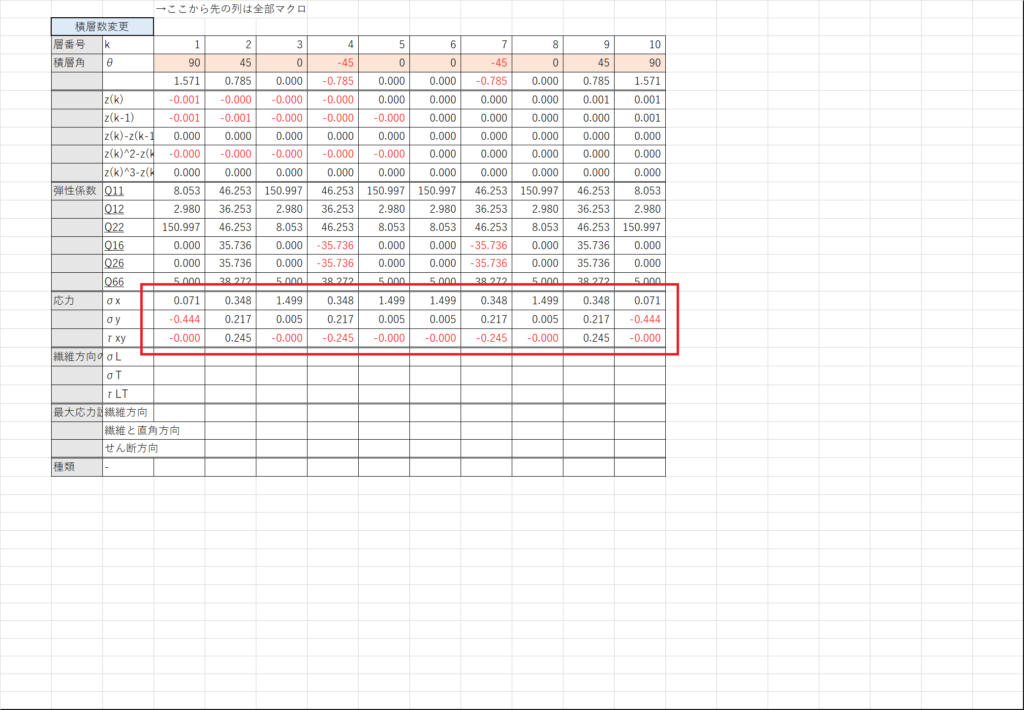
式(C1)で破断するかどうか調べる
まず,xy方向の応力をLT方向に変換する
変換式は(序)p.83で次のように与えられる
\begin{eqnarray}
\sigma_{L}&=&\sigma_{x}l^2+\sigma_{y}m^2+2\tau_{xy}lm \\
\sigma_{T}&=&\sigma_{x}m^2+\sigma_{y}l^2-2\tau_{xy}lm \\
\tau_{LT}&=&-\sigma_{x}lm+\sigma_{y}lm+\tau_{xy}(l^2-m^2)
\tag{4.52}
\end{eqnarray}
ただし,\(l=cos{\theta}, m=sin{\theta} \)
セルX20~X22で式(4.52)を計算する
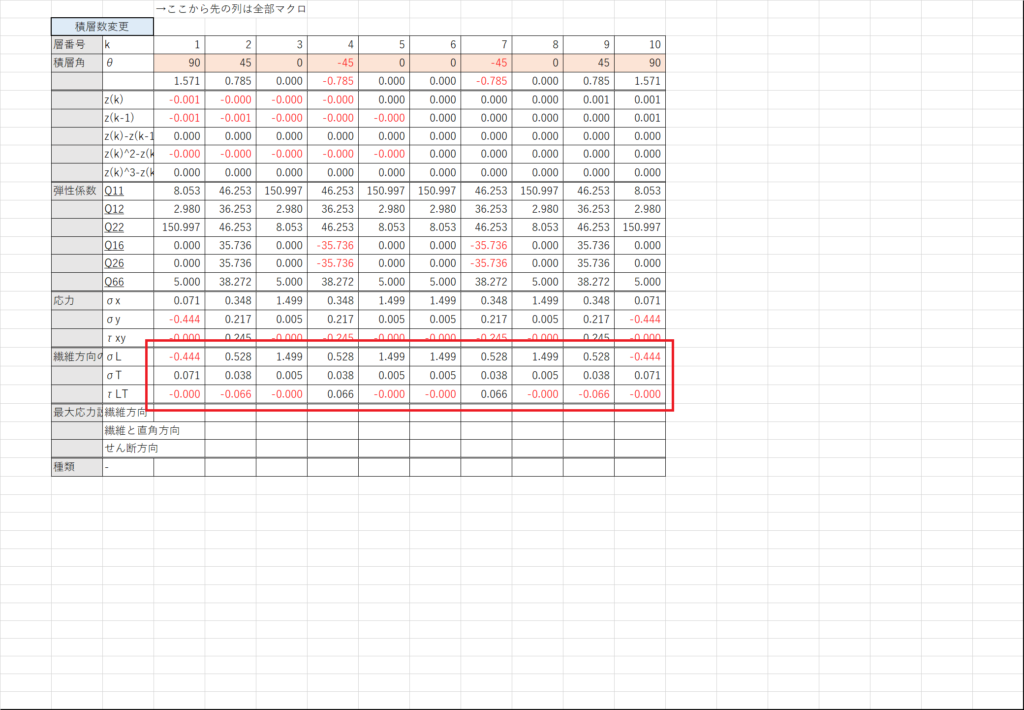
セルX23~X25~で式(C1)を計算する
ここでは場合分けを行って,応力が0の場合には何も表示しない,応力が負の場合には応力を圧縮強度で割った値を表示,応力が正の場合には応力を引張強度で割った値を表示する
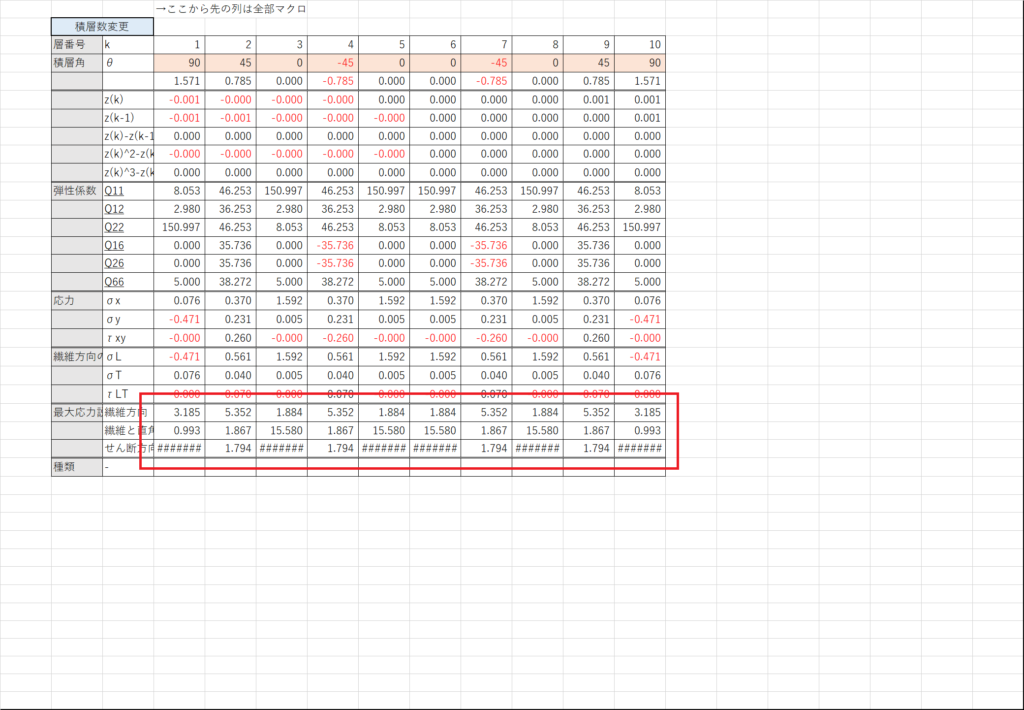
ついでに,応力/強度が1を下回ったときにセルの色を変えるようにしておく
「ホーム→セルの強調表示ルール→規定の値より小さい」を選択
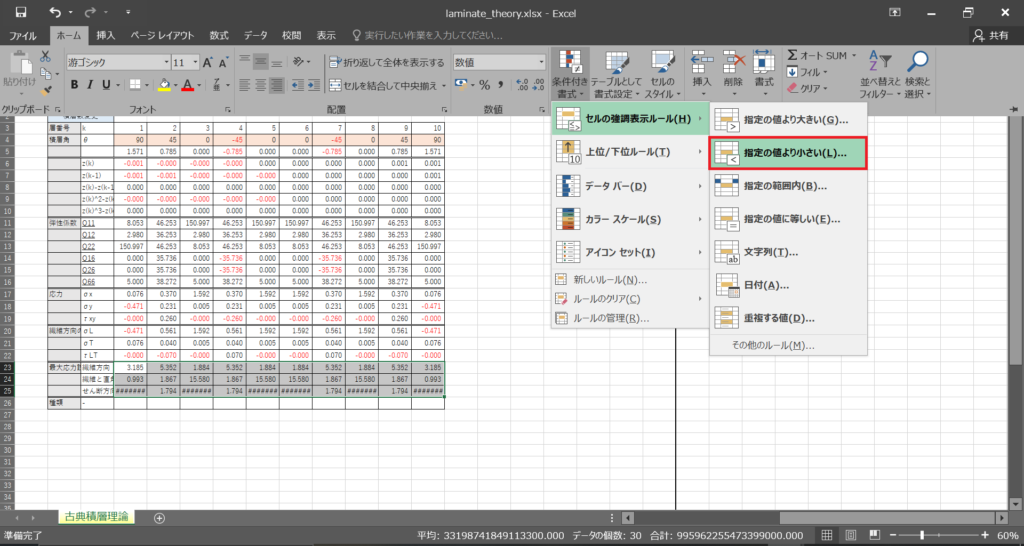
1より小さい値のとき明るい赤の背景になるようにして「OK」を選択
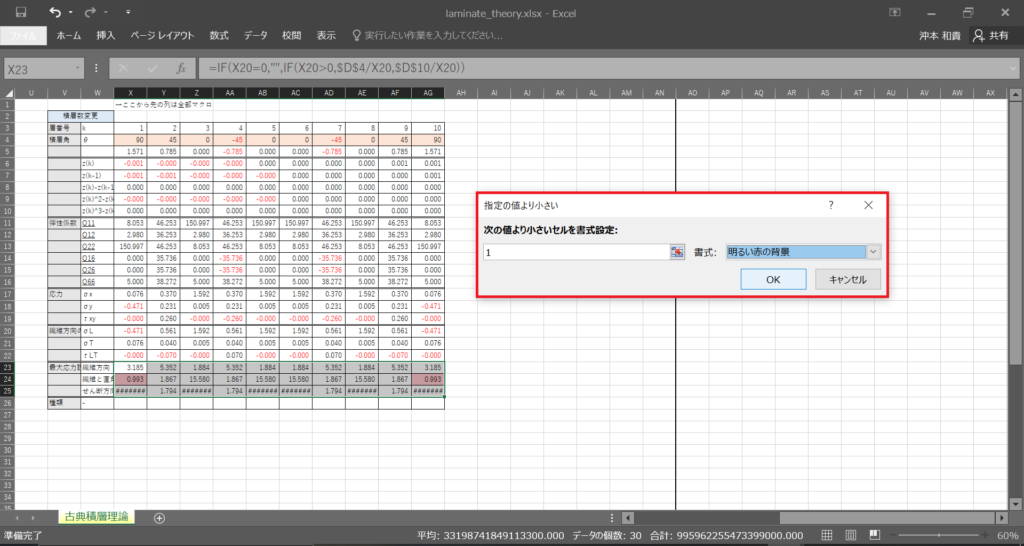
これで見えやすくなった
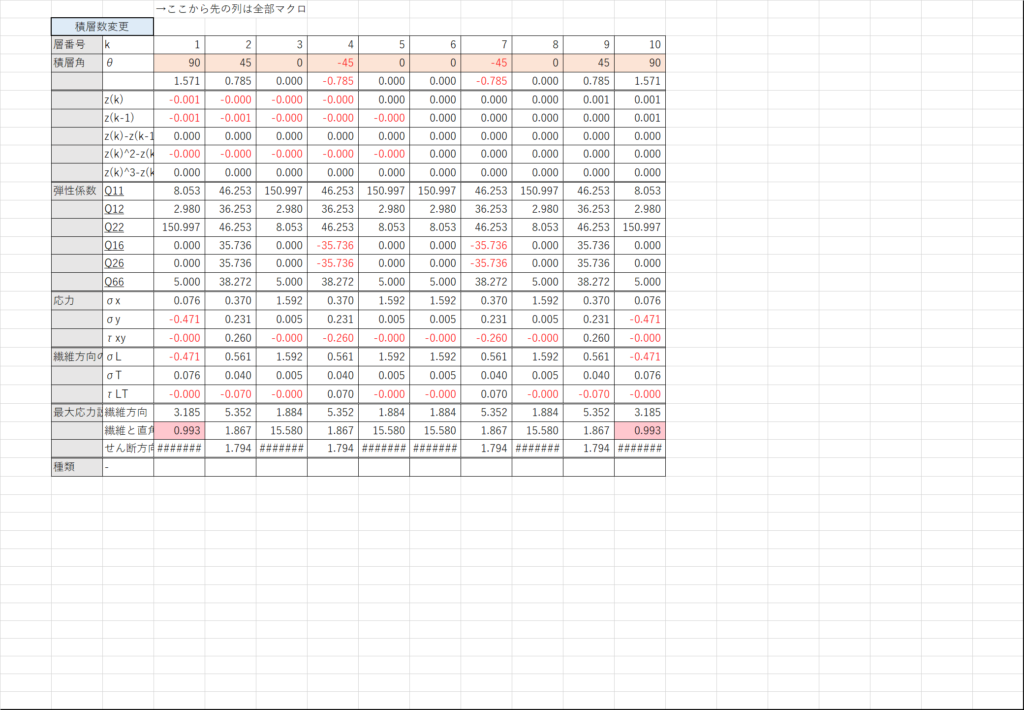
これで今回の目的は達成できた
まとめ
最大応力説の計算には「応力が一方向にしかはたらいていない」という仮定がある
したがって,主翼のように曲げ(引張・圧縮)とねじれ(剪断)が同時に作用する場合は結果が変わってくる場合があることに注意しなければならない
参考資料には他の破損則も載っているのでぜひ見てみてほしい
↓次の記事
↓記事一覧






コメント
設計シート作成、大変参考にさせていただいています。
他の古典積層理論の資料を見ていて気付いたのですが、式(4.52)右辺第3項のl^2+m^2は(1になっちゃうので)正しくはl^2-m^2になりそうです。
ご指摘いただきありがとうございます!
(l^2-m^2)が正しいことを確認しましたので、修正いたしました。