PR

CST Airfoilを作成するPythonプログラム

CST（Class-Shape Transformation）法を使用して翼型の形状を生成したり、既存の翼型にCSTパラメータをフィッティングさせたりするpythonプログラムを作った

mtkbirdman.com/MDO/CST.py at master · mtkbirdman/mtkbirdman.com
mtk_birdman's blog ＠mtk_birdman. Contribute to mtkbirdman/mtkbirdman.com development by creating an account on GitHub.
github.com
スポンサーリンク

はじめに

CST（Class-Shape Transformation）法を使用して翼型の形状を生成したり、既存の翼型にCSTパラメータをフィッティングさせたりするpythonプログラムを作った

↓論文

Just a moment...
arc.aiaa.org

↓参考

GitHub - Ry10/Kulfan_CST: Used to get the airfoil coordinates from Kulfan parameters or to get the Kulfan parameters from known airfoil coordinates. Uses the CST method.
Used to get the airfoil coordinates from Kulfan parameters or to get the Kulfan parameters from known airfoil coordinate...
github.com
CST Airfoil – OpenVSP Ground School
vspu.larc.nasa.gov
CST Airfoil Geometry — pyGeo documentation
mdolab-pygeo.readthedocs-hosted.com

それではいってみよう

ソースコードの解説

mtkbirdman.com/MDO/CST.py at master · mtkbirdman/mtkbirdman.com
mtk_birdman's blog ＠mtk_birdman. Contribute to mtkbirdman/mtkbirdman.com development by creating an account on GitHub.
github.com
 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import minimize
import random
import math
from scipy.interpolate import interp1d

class CST:
  def __init__(self):
    self.wl = None
    self.wu = None
    self.dz = None
    self.Node = None
    self.x = None
    self.y = None
    self.coord = None
    self.x_old = None
    self.y_old = None
    self.xt = None
    self.yt = None
    self.ler = None
    self.n_wl = None
    self.n_wu = None

  def _class_shape(self, w, x, N1, N2, dz):
    C = x**N1 * (1 - x)**N2 # Class function
    # Shape function; using Bernstein Polynomials
    S = np.zeros_like(x)
    nw = w.shape[1] - 1 # Order of Bernstein polynomials
    K = np.zeros(nw+1)
    for i in range(0, nw+1):
      K[i] = math.factorial(nw)/(math.factorial(i)*(math.factorial((nw)-(i))))
    for j in range(0, nw+1):
      S += (w[:,j]*K[j]).reshape(-1,1)*x**(j) * ((1-x)**(nw-(j)))
    y = C * S + x * dz
    return y

  def create_airfoil(self, wl=[[-1, -1, -1]], wu=[[1, 1, 1]], dz=[0], Node=100):
    self.wl = np.array(wl)
    self.wu = np.array(wu)
    self.dz = np.array(dz).reshape(-1,1)
    self.Node = Node
    N = self.dz.shape[0]

    if self.x is None: # Create x coordinate
      self.x = np.ones((N,self.Node))
      zeta = np.zeros((N,self.Node))
      for i in range(self.Node):
        zeta[:, i] = 2 * np.pi / (self.Node - 1)*i
        self.x[:, i] = 0.5 * (np.cos(zeta[:, i])+ 1)
    # Ni and N2 parameters (N1 = 0.5 and N2 = 1 for airfoil shape)
    N1 = 0.5
    N2 = 1

    center_loc = np.argmin(self.x)
    xu = self.x[:,:center_loc]
    xl = self.x[:,center_loc:]
    yu = self._class_shape(self.wu, xu, N1, N2, self.dz)
    yl = self._class_shape(self.wl, xl, N1, N2, -self.dz)

    self.x = np.concatenate([xu, xl],axis=1).reshape(N,-1)
    self.y = np.concatenate([yu, yl],axis=1).reshape(N,-1)
    self.coord = np.stack([self.x, self.y],axis=1)
    return self.coord

  def write_to_file(self, file_name = 'airfoil_shape.csv', N=0):
    df = pd.DataFrame(self.coord[N].T, columns=['x', 'y'])
    df.to_csv(file_name, header=True, index=False)

  def fit_CST(self, file_name = 'airfoil_shape.csv', n_wl=4, n_wu=4):
    data = pd.read_csv(file_name)
    self.x_old = data['x'].to_numpy()
    self.y_old = data['y'].to_numpy()
    self.Node = len(data)
    self.dz = [abs(self.y_old[-1])]
    self.n_wl = n_wl
    self.n_wu = n_wu
    # normalization
    self.x_old = self.x_old/(np.max(self.x_old)-np.min(self.x_old))
    self.x_old = self.x_old-np.min(self.x_old)
    self.y_old = self.y_old/(np.max(self.x_old)-np.min(self.x_old))
    self.x = self.x_old.reshape(1,-1)
    initial_guess = [random.uniform(-1,1) for _ in range(self.n_wl+self.n_wu)]
    result = minimize(self._objfunc, initial_guess) # minimize
    
    self.x=None
    self.create_airfoil(wl=self.wl, wu=self.wu, dz=self.dz, Node=self.Node)

  def _objfunc(self, x):
    wl = [x[:self.n_wl]]
    wu = [x[self.n_wl:self.n_wl + self.n_wu]]
    self.create_airfoil(wl=wl, wu=wu, dz=[0], Node=self.Node)
    f = np.sum((self.y * 100 - self.y_old * 100)**2)
    return f

  def get_var(self):
    return self.wu, self.wl

  def get_thickness(self):
    thickness = []
    x_tmax = []
    self.xt = np.zeros_like(self.x)
    self.yt = np.zeros_like(self.y)
    for N in range(self.coord.shape[0]):
      center_loc = np.argmin(self.coord[N,0])
      coord_u = self.coord[N, :, :center_loc+1]
      coord_l = self.coord[N, :, center_loc:]
      
      fl = interp1d(coord_l[0,:], coord_l[1,:], kind= 'linear')
      self.xt[N,:center_loc+1] = coord_u[0,:]
      self.yt[N,:center_loc+1] = coord_u[1,:]-fl(coord_u[0,:])

      fu = interp1d(coord_u[0,:], coord_u[1,:], kind='linear')
      self.xt[N,center_loc:] = coord_l[0,:]
      self.yt[N,center_loc:] = fu(coord_l[0,:])-coord_l[1,:]
      thickness.append(np.max(self.yt[N]))
      x_tmax.append(self.xt[N,np.argmax(self.yt[N])])

    return np.array(thickness),np.array(x_tmax)

  def get_ler(self):
    if self.yt is None: 
      self.get_thickness()
    self.ler = np.zeros(self.coord.shape[0])
    for N in range(self.coord.shape[0]):
      x0 = np.min(self.xt[N])
      y0 = self.yt[N,np.argmin(self.xt[N])]/2
      r = ((self.xt[N]-x0)**2+(-y0)**2)**0.5
      center_loc = np.argmin(self.xt[N])
      for i in range(center_loc,r.shape[0]):
        d = ((self.xt[N,:]-self.xt[N,i])**2+(self.yt[N,:]/2-y0)**2)**0.5

        if r[i]>np.min(d):
          self.ler[N] = r[i-1]
          break
    return self.ler
  
  def get_TE_angle(self):
    if self.yt is None: 
      self.get_thickness()
    TE_angle = []
    for N in range(self.coord.shape[0]):
      center_loc = np.argmin(self.coord[N,0])
      f = interp1d(self.xt[N,:center_loc+1], self.yt[N,:center_loc+1], kind= 'linear')
      x90 = 0.90
      x99 = 0.99
      y90 = f(x90)
      y99 = f(x99)
      TE_angle.append(math.degrees(math.atan2(abs(y90-y99),abs(x90-x99))))

    return np.array(TE_angle)

  def get_section_area(self):
    if self.yt is None: 
      self.get_thickness()
    
    x_diff = np.abs(np.diff(self.xt,n=1,axis=1))
    section_area = np.sum(x_diff * self.yt[:,1:],axis=1)/2

    return section_area
  
  def plot(self,N=0):
    fig, ax = plt.subplots()
    ax.plot(self.x[N], self.y[N],label='CST')
    if self.y_old is not None:
      ax.plot(self.x_old, self.y_old,label='original')
    if self.ler is not None:
      theta = np.linspace(0, 2 * np.pi, 100)
      #中心と半径から円の座標を計算
      x = self.ler[N] + self.ler[N] * np.cos(theta)
      y = self.ler[N] * np.sin(theta)
      ax.plot(x, y,label='ler')
      ax.plot(self.xt[N], self.yt[N]/2,label='Symmetry')
    ax.set_aspect("equal", "box")
    ax.set_xlim(0, 1)
    ax.set_ylim(-0.5, 0.5)
    ax.set_xlabel( 'x/c')
    ax.set_ylabel( 'y/c')
    ax.spines[ 'right'] .set_visible(False)
    ax.spines[ 'top'] .set_visible(False)
    ax.yaxis.set_ticks_position( 'left')
    ax.xaxis.set_ticks_position( 'bottom')
    ax.legend()
    ax.plot
    plt.show()

if __name__ == '__main__':
  airfoil = CST()
  airfoil.fit_CST(file_name='./CST/NACA4412.csv')
  thickness, x_tmax = airfoil.get_thickness()
  ler = airfoil.get_ler()
  TE_angle = airfoil.get_TE_angle()
  section_area = airfoil.get_section_area()
  airfoil.plot(N=0)
  wu = airfoil.wu
  wl = airfoil.wl
  airfoil.write_to_file()
  print(wu,wl)
  print(thickness,x_tmax,ler,TE_angle)
  print(section_area)

このプログラムは、CST（Class-Shape Transformation）法を使用して翼型の形状を生成したり、既存の翼型に対してCSTパラメータをフィッティングさせたりするクラスを実装している

また、翼型の幾何学的特性を計算し、プロットするための機能も含まれている

このプログラムはのちのち最適化に使うことを想定しているため、バッチ処理に対応しており、すべての変数は[:, n]のような二次元以上の配列になっている

依存ライブラリ

プログラムは以下のライブラリに依存している

  • numpy
  • pandas
  • matplotlib
  • scipy
  • random
  • math

CST クラス

__init__ メソッド
  def __init__(self):
    self.wl = None
    self.wu = None
    self.dz = None
    self.Node = None
    self.x = None
    self.y = None
    self.coord = None
    self.x_old = None
    self.y_old = None
    self.xt = None
    self.yt = None
    self.ler = None
    self.n_wl = None
    self.n_wu = None

引数: なし

処理:

CSTクラスのインスタンスを初期化し、翼型のパラメータと座標を格納するための属性を定義する

  • wl, wu: 下側と上側のCSTパラメータ
  • dz: 翼型の後縁厚さ
  • Node: 翼型の節点数
  • x, y: 翼型のx座標とy座標
  • coord: 翼型の座標
  • x_old, y_old: ベース翼型のx座標とy座標
  • xt, yt: 厚みの計算に使用するx座標とy座標
  • ler: 前縁半径
  • n_wl, n_wu: 下側と上側のCSTパラメータの数

返り値: なし

_class_shape メソッド
  def _class_shape(self, w, x, N1, N2, dz):
    C = x**N1 * (1 - x)**N2 # Class function
    # Shape function; using Bernstein Polynomials
    S = np.zeros_like(x)
    nw = w.shape[1] - 1 # Order of Bernstein polynomials
    K = np.zeros(nw+1)
    for i in range(0, nw+1):
      K[i] = math.factorial(nw)/(math.factorial(i)*(math.factorial((nw)-(i))))
    for j in range(0, nw+1):
      S += (w[:,j]*K[j]).reshape(-1,1)*x**(j) * ((1-x)**(nw-(j)))
    y = C * S + x * dz
    return y

引数:

  • w: ndarray - CSTパラメータ
  • x: ndarray - x座標
  • N1: float - クラス関数のパラメータ1
  • N2: float - クラス関数のパラメータ2
  • dz: float - 翼型の後縁厚さ

処理:

  • クラス関数 C を x**N1 * (1 - x)**N2 で計算
  • 形状関数 S を計算
  • C と S を組み合わせて y を計算

返り値:

  • y: ndarray - 計算されたy座標
create_airfoil メソッド
  def create_airfoil(self, wu=[[-1, -1, -1]], wl=[[1, 1, 1]], dz=[0], Node=101):
    self.wl = np.array(wl)
    self.wu = np.array(wu)
    self.dz = np.array(dz).reshape(-1,1)
    self.Node = Node
    N = self.dz.shape[0]

    if self.x is None: # Create x coordinate
      self.x = np.ones((N,self.Node))
      zeta = np.zeros((N,self.Node))
      for i in range(self.Node):
        zeta[:, i] = 2 * np.pi / (self.Node - 1)*i
        self.x[:, i] = 0.5 * (np.cos(zeta[:, i])+ 1)
    # Ni and N2 parameters (N1 = 0.5 and N2 = 1 for airfoil shape)
    N1 = 0.5
    N2 = 1

    center_loc = np.argmin(self.x)
    xu = self.x[:,:center_loc]
    xl = self.x[:,center_loc:]
    yu = self._class_shape(self.wu, xu, N1, N2, self.dz)
    yl = self._class_shape(self.wl, xl, N1, N2, -self.dz)

    self.x = np.concatenate([xu, xl],axis=1).reshape(N,-1)
    self.y = np.concatenate([yu, yl],axis=1).reshape(N,-1)
    self.coord = np.stack([self.x, self.y],axis=1)
    return self.coord

引数:

  • wl: list - 下面のCSTパラメータ
  • wu: list - 上面のCSTパラメータ
  • dz: list - 翼型の後縁厚さ
  • Node: int - x座標の分割数

処理:

  • CSTパラメータと後縁厚さを設定
  • x座標を計算
  • クラス関数と形状関数を用いて上面と下面のy座標を計算
  • 上面と下面の座標を結合して翼型の座標を生成

返り値:

  • self.coord: ndarray - 生成された翼型の座標

節点数が奇数なら(0,0)に前縁点を持ってくることができる

write_to_file メソッド
  def write_to_file(self, file_name = 'airfoil_shape.csv', N=0):
    df = pd.DataFrame(self.coord[N].T, columns=['x', 'y'])
    df.to_csv(file_name, header=True, index=False)

引数:

  • file_name: str - 保存するファイル名
  • N: int - 保存する翼型のインデックス

処理:

  • self.coord から指定された翼型の座標を取得
  • DataFrameに変換し、CSVファイルに保存

返り値: なし

fit_CST メソッド
  def fit_CST(self, file_name = 'airfoil_shape.csv', n_wl=4, n_wu=4):
    data = pd.read_csv(file_name)
    self.x_old = data['x'].to_numpy()
    self.y_old = data['y'].to_numpy()
    self.Node = len(data)
    self.dz = [abs(self.y_old[-1])]
    self.n_wl = n_wl
    self.n_wu = n_wu
    # normalization
    self.x_old = self.x_old/(np.max(self.x_old)-np.min(self.x_old))
    self.x_old = self.x_old-np.min(self.x_old)
    self.y_old = self.y_old/(np.max(self.x_old)-np.min(self.x_old))
    self.x = self.x_old.reshape(1,-1)
    initial_guess = [random.uniform(-1,1) for _ in range(self.n_wl+self.n_wu)]
    result = minimize(self._objfunc, initial_guess) # minimize
    
    self.x=None
    self.create_airfoil(wl=self.wl, wu=self.wu, dz=self.dz, Node=self.Node)

引数:

  • file_name: str - 翼型データのCSVファイル名
  • n_wl: int - 下面のCSTパラメータの数
  • n_wu: int - 上面のCSTパラメータの数

処理:

  • CSVファイルから対象の翼型データを読み込む
  • x座標が前縁(0,0)、後縁(1,0)になるようにデータを正規化する
  • 最適化の初期値を設定する（-1から1の範囲で適当に生成した乱数）
  • scipy.optimizeの最適化メソッドminimizeを使用して、元の翼型と生成した翼型の二乗和誤差が最小になるようにCSTパラメータを求める
  • 最適化されたCSTパラメータを使用して翼型を再生成する

返り値: なし

↓参考

Kulfan_CST/coord_to_kulfan.py at master · Ry10/Kulfan_CST
Used to get the airfoil coordinates from Kulfan parameters or to get the Kulfan parameters from known airfoil coordinate...
github.com
_objfunc メソッド
  def _objfunc(self, x):
    wl = [x[:self.n_wl]]
    wu = [x[self.n_wl:self.n_wl + self.n_wu]]
    self.create_airfoil(wl=wl, wu=wu, dz=[0], Node=self.Node)
    f = np.sum((self.y * 100 - self.y_old * 100)**2)
    return f

このプライベートメソッドは、fit_CSTメソッドにおいて元の翼型と生成した翼型の二乗和誤差が最小になるようにCSTパラメータを求める際に用いられる

引数:

  • x: list - 最適化のための変数

処理:

  • 下側と上側のCSTパラメータを設定する
  • 与えられたCSTパラメータで翼型を生成する
  • 生成された翼型と元の翼型との誤差を計算する

返り値:

  • f: float - 誤差の二乗和
get_var メソッド
  def get_var(self):
    return self.wu, self.wl

引数: なし

処理: 上面と下面の現在のCSTパラメータを取得

返り値:

  • self.wu: ndarray - 上面のCSTパラメータ
  • self.wl: ndarray - 下面のCSTパラメータ
get_thickness メソッド
  def get_thickness(self):
    thickness = []
    x_tmax = []
    self.xt = np.zeros_like(self.x)
    self.yt = np.zeros_like(self.y)
    for N in range(self.coord.shape[0]):
      center_loc = np.argmin(self.coord[N,0])
      coord_u = self.coord[N, :, :center_loc+1]
      coord_l = self.coord[N, :, center_loc:]
      
      fl = interp1d(coord_l[0,:], coord_l[1,:], kind= 'linear')
      self.xt[N,:center_loc+1] = coord_u[0,:]
      self.yt[N,:center_loc+1] = coord_u[1,:]-fl(coord_u[0,:])

      fu = interp1d(coord_u[0,:], coord_u[1,:], kind='linear')
      self.xt[N,center_loc:] = coord_l[0,:]
      self.yt[N,center_loc:] = fu(coord_l[0,:])-coord_l[1,:]
      thickness.append(np.max(self.yt[N]))
      x_tmax.append(self.xt[N,np.argmax(self.yt[N])])

    return np.array(thickness),np.array(x_tmax)

引数: なし

処理:

  • 翼型について、上面と下面の厚みを計算
  • 最大厚みとその位置を計算

返り値:

  • thickness: ndarray - 翼厚の配列
  • x_tmax: ndarray - 最大翼厚の位置の配列
get_ler メソッド
  def get_ler(self):
    if self.yt is None: 
      self.get_thickness()
    self.ler = np.zeros(self.coord.shape[0])
    for N in range(self.coord.shape[0]):
      x0 = np.min(self.xt[N])
      y0 = self.yt[N,np.argmin(self.xt[N])]/2
      r = ((self.xt[N]-x0)**2+(-y0)**2)**0.5
      center_loc = np.argmin(self.xt[N])
      for i in range(center_loc,r.shape[0]):
        d = ((self.xt[N,:]-self.xt[N,i])**2+(self.yt[N,:]/2-y0)**2)**0.5

        if r[i]>np.min(d):
          self.ler[N] = r[i-1]
          break
    return self.ler

引数: なし

処理:

  • self.yt が未計算の場合、 get_thickness を呼び出して翼厚を計算
  • 各翼型について、前縁半径を計算

返り値:

  • self.ler: ndarray - 前縁半径の配列

節点数が少ないと露骨に精度が落ちるので、節点数は200点くらいあると安心

get_TE_angle メソッド
  def get_TE_angle(self):
    if self.yt is None: 
      self.get_thickness()
    TE_angle = []
    for N in range(self.coord.shape[0]):
      center_loc = np.argmin(self.coord[N,0])
      f = interp1d(self.xt[N,:center_loc+1], self.yt[N,:center_loc+1], kind= 'linear')
      x96 = 0.96
      x99 = 0.99
      y96 = f(x96)
      y99 = f(x99)

      TE_angle.append(math.degrees(math.atan2(abs(y96-y99),abs(x96-x99))))

    return np.array(TE_angle)

引数: なし

処理:

  • self.yt が未計算の場合、 get_thickness を呼び出して翼厚を計算
  • 翼型について、後縁角を計算

返り値:

  • TE_angle: ndarray - 後縁角の配列
get_section_area メソッド
  def get_section_area(self):
    if self.yt is None: 
      self.get_thickness()
    
    x_diff = np.abs(np.diff(self.xt,n=1,axis=1))
    section_area = np.sum(x_diff * self.yt[:,1:],axis=1)/2

    return section_area

引数: なし

処理:

  • self.yt が未計算の場合、 get_thickness を呼び出して翼厚を計算
  • 翼型について、断面積を計算

返り値:

  • section_area: ndarray - 断面積の配列
plot メソッド
  def plot(self,N=0):
    fig, ax = plt.subplots()
    ax.plot(self.x[N], self.y[N],label='CST')
    if self.y_old is not None:
      ax.plot(self.x_old, self.y_old,label='original')
    if self.ler is not None:
      theta = np.linspace(0, 2 * np.pi, 100)
      #中心と半径から円の座標を計算
      x = self.ler[N] + self.ler[N] * np.cos(theta)
      y = self.ler[N] * np.sin(theta)
      ax.plot(x, y,label='ler')
      ax.plot(self.xt[N], self.yt[N]/2,label='Symmetry')
    ax.set_aspect("equal", "box")
    ax.set_xlim(0, 1)
    ax.set_ylim(-0.5, 0.5)
    ax.set_xlabel( 'x/c')
    ax.set_ylabel( 'y/c')
    ax.spines[ 'right'] .set_visible(False)
    ax.spines[ 'top'] .set_visible(False)
    ax.yaxis.set_ticks_position( 'left')
    ax.xaxis.set_ticks_position( 'bottom')
    ax.legend()
    ax.plot
    plt.show()

引数:

  • N: int - プロットする翼型のインデックス

処理:

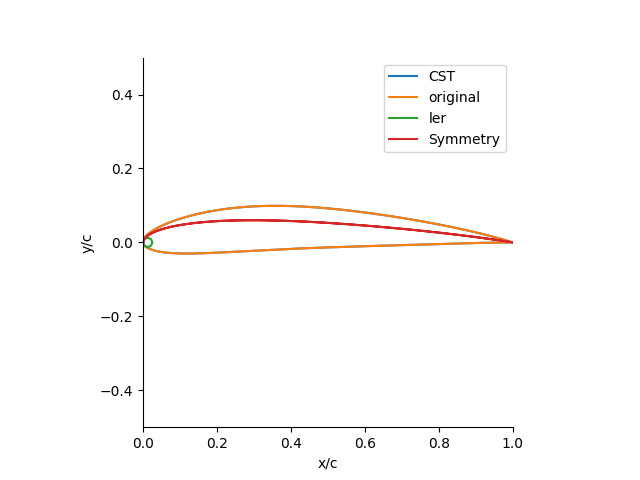
  • 指定された翼型をプロット
  • フィッティングした際に、元の翼型データが存在する場合、それもプロット
  • 前縁半径と仮想的な対称翼型をプロット

返り値: なし

メインプログラム

if __name__ == '__main__':
  airfoil = CST()
  airfoil.fit_CST(file_name='./CST/NACA4412.csv')
  thickness, x_tmax = airfoil.get_thickness()
  ler = airfoil.get_ler()
  TE_angle = airfoil.get_TE_angle()
  section_area = airfoil.get_section_area()
  airfoil.plot(N=0)
  wu = airfoil.wu
  wl = airfoil.wl
  
  print(wu,wl)
  print(thickness,x_tmax,ler,TE_angle)
  print(section_area)
  
  airfoil.write_to_file()

このセクションは、スクリプトとして実行されたときに実行される

  1. CST クラスのインスタンスを作成する
  2. fit_CST メソッドを使用して、指定されたCSVファイルから翼型データを読み込み、CSTパラメータにフィッティングさせる
  3. 各種メソッドを使用して翼型の形状を取得する
  4. plot メソッドを使用して翼型をプロットする
  5. 結果をCSVファイルに保存し、計算結果を表示する

使い方

CSTパラメータをフィッティングさせたい翼型を.csvファイルにして、CST.pyと同じディレクトリに置く

__main__関数の中のairfoil.fit_CST()の引数のfile_nameを適当に書き換える

airfoil.fit_CST(file_name='./NACA4412.csv')

あとはターミナルで以下のコマンドを実行する

> py -3.10 CST.py

標準出力としてCSTパラメータなどが表示されるので、あとは煮るなり焼くなり好きにすればいい

↓最適化で使いたい場合はこっちを参照

pymooのNSGA-IIとxfoilでCST翼型の多目的最適化を行う
pymooのNSGA-IIとxfoilでCST Airfoilの多目的最適化を行う
mtkbirdman.com
2024.05.24

おわりに

CST（Class-Shape Transformation）法を使用して翼型の形状を生成したり、既存の翼型にCSTパラメータをフィッティングさせたりするpythonプログラムを作った

翼型の形状を少ないパラメータ数でいい感じに表現できるので、最適化なりモデリングなりで楽しく使えそうである

↓関連記事

いろいろな翼型の圧力分布
翼型の圧力分布を理解するために、圧力分布の基本といろいろな翼型の圧力分布を紹介する
mtkbirdman.com
2024.03.27
CMPLXFOILで翼型の最適化を行う
CMPLXFOILを使って2次元翼型の最適化を行う
mtkbirdman.com
2022.10.22

スポンサーリンク

コメント