寸法のばらつきを理解し,公差の集積を計算するための方法について説明する
公差のばらつきは3σ、公差の積み上げは分散の加法性に基づく二乗和平方根で計算できる
— いーそー (@mtk_birdman) January 19, 2023
ほーん
部品の寸法には「ばらつき」が存在する
部品の寸法には「ばらつき」が存在する
組立品は,それぞれの部品が持つ寸法のばらつきを考慮して設計されなければならない
図面上ではそのようば寸法のばらつきは「公差」で指定され,寸法のばらつきがその公差内に収まっていれば,正しく組み立てられるようになっている
ばらつきとは統計学における標準偏差である
今回は部品のばらつきが正規分布に従っていると仮定する
正規分布とは,その名の通りだいたいの物事にあてはまる最もありふれたばらつきの分布である
例えば,文科省が公開している日本人男性17歳の身長の分布はほとんど正規分布に従う
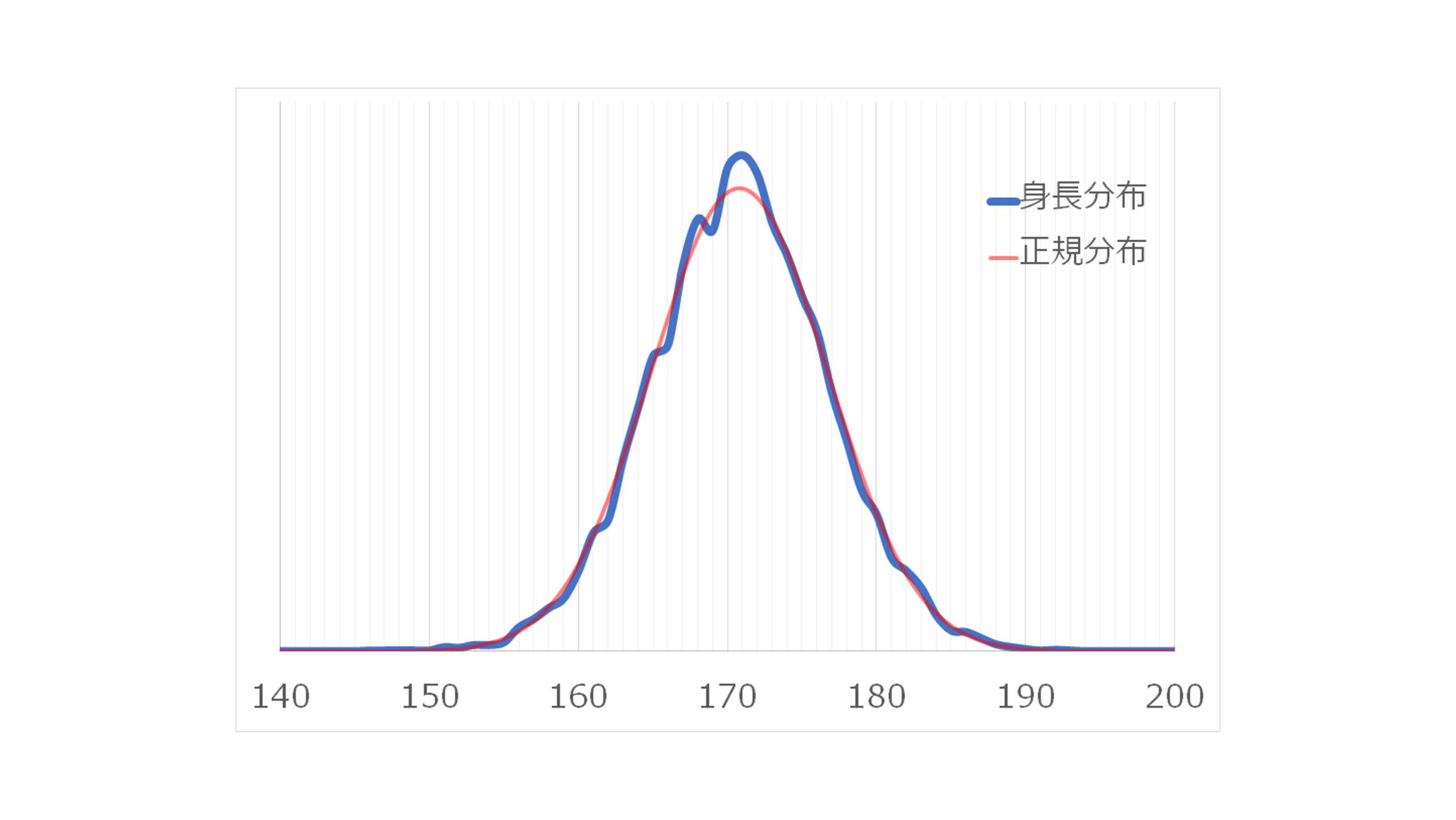
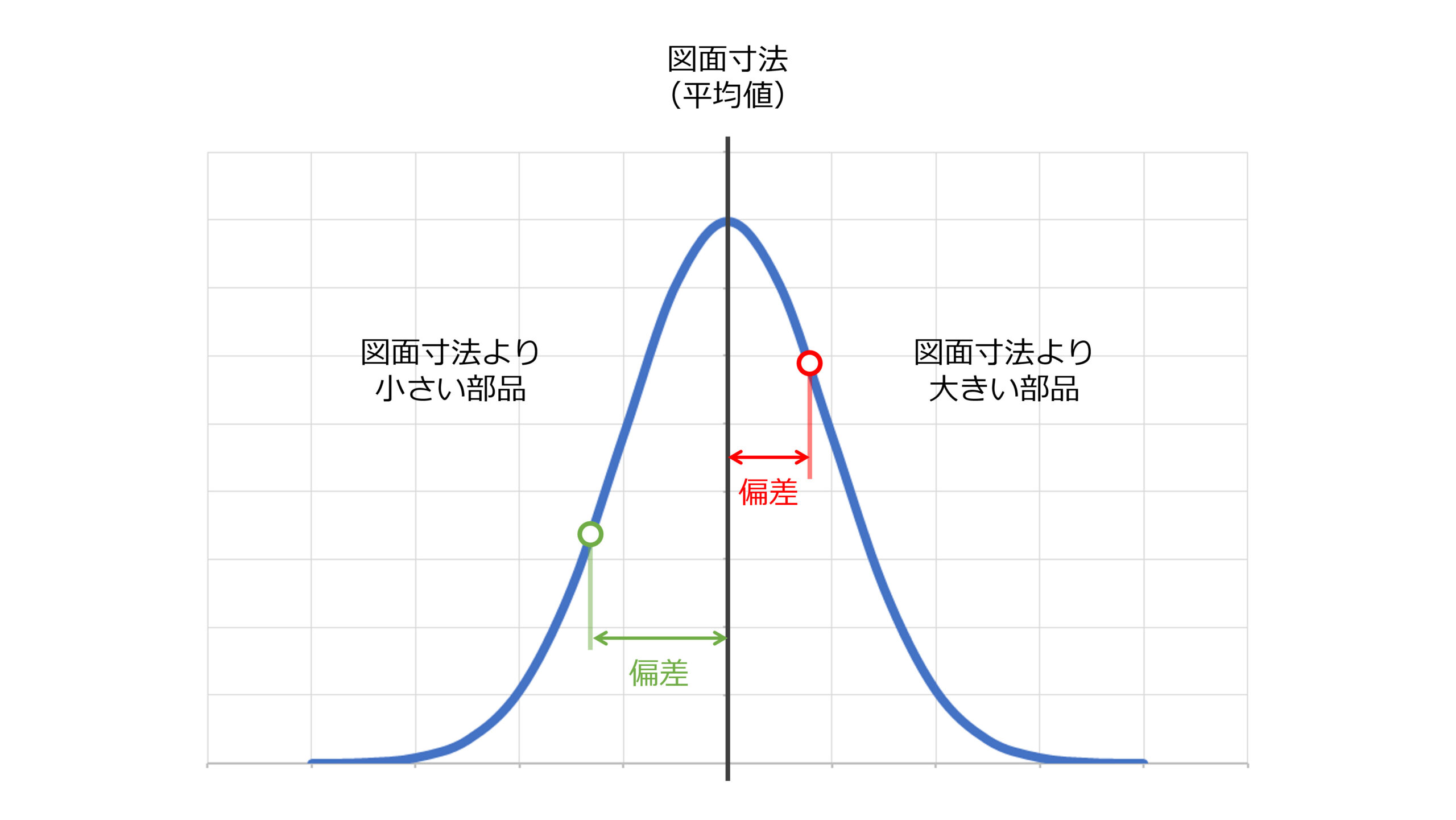
ここで,個々の部品のばらつきは偏差として表現できる
偏差は個々の数値\(x_{i}\)と平均\(\mu\)との差で表される
\begin{equation}
x_{i}-\mu
\end{equation}
平均\(\mu\)は次のように計算できる
\begin{equation}
\mu=\frac{\sum{x_{i}}}{n}
\end{equation}
部品全体のばらつきの大きさを表す指標には分散と標準偏差があるが,今回は寸法の値と同じ単位をもつ標準偏差の方を用いる
部品のばらつき(偏差)はプラスもあればマイナスもあるので,全体の傾向を見るために単純に平均を取ってしまうと,その値はほぼゼロになってしまう
平均がほぼゼロになってしまうことを避けるために,偏差を二乗してから平均を取ったものが分散である
分散は次の式で表される
\begin{equation}
\frac{\sum{\left(x_{i}-\mu\right)^2}}{n}
\end{equation}
分散の値が大きければ大きいほど,部品のばらつきが大きいことを意味する
分散は部品のばらつきの大きさを表すことのできる一つの指標だが,単位が㎟になってしまい直感性に欠ける
そこで,分散を計算するときの2乗を打ち消すために,分散の平方根を取ったものが標準偏差である
標準偏差\(\sigma\)は次の式で表される
\begin{equation}
\sigma=\sqrt{\frac{\sum{\left(x_{i}-\mu\right)^2}}{n}}
\end{equation}
標準偏差とは「それぞれの部品の偏差を二乗してから平均を取ったものの平方根」であり,ざっくり「全部品の偏差の平均値」みたいなものだと思ってもらえばいい
標準偏差が大きければ大きいほど,部品のばらつきが大きいことを意味する
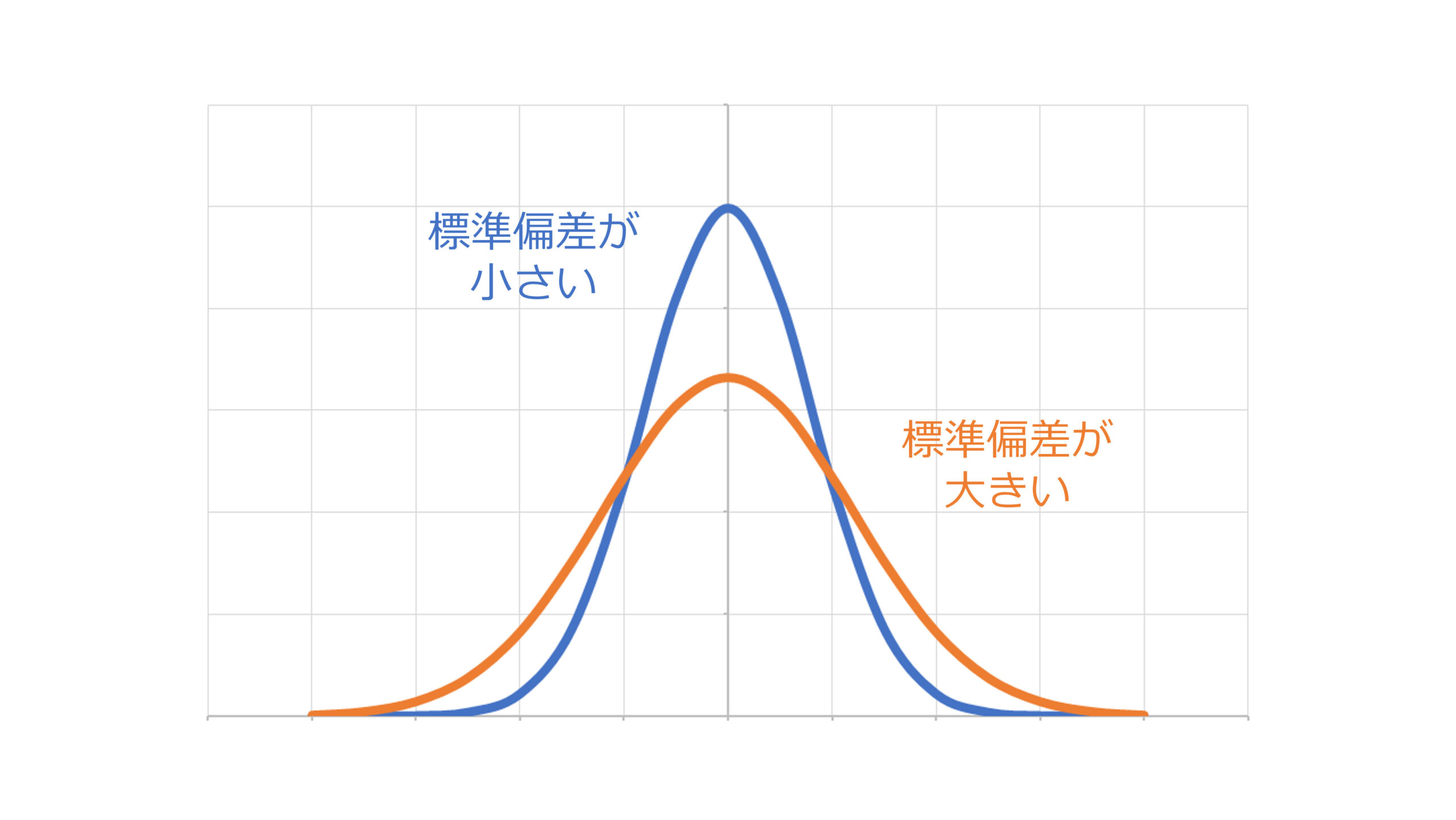
公差は\(3\sigma\)(標準偏差の3倍)として設定する
部品の寸法のばらつきの大きさ度合いは標準偏差で表されることが分かった
次はこの標準偏差を公差という図面要求に落とし込む必要がある
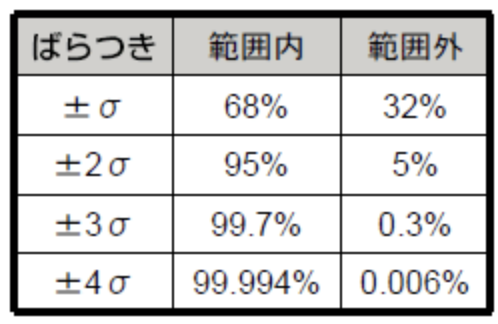
正規分布に従っている部品の寸法のばらつきが,\(\pm{\sigma}\)の範囲に収まる確率は65%である
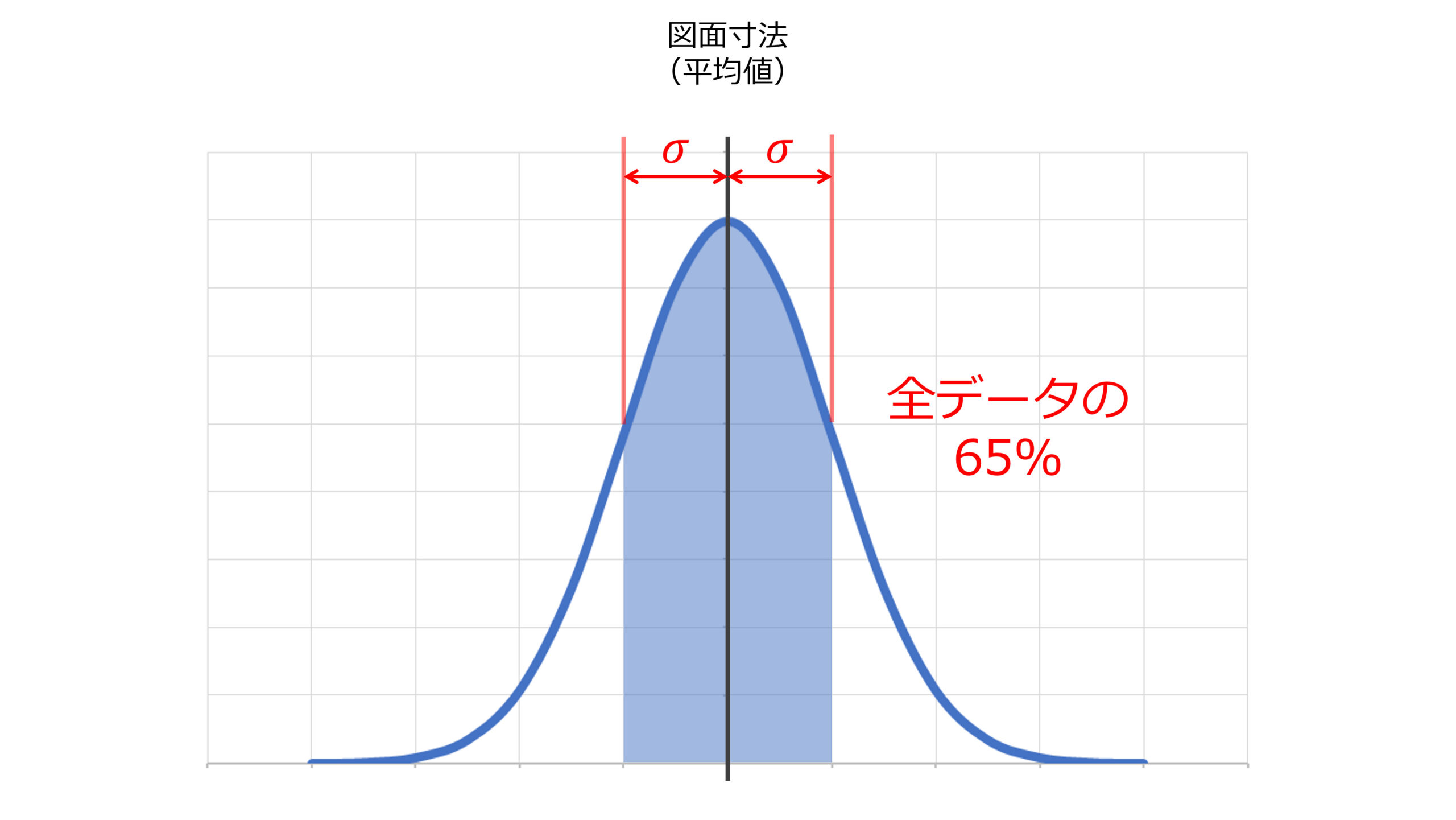
同様に,部品の寸法のばらつきが\(\pm{2\sigma}\)の範囲に収まる確率は95%,\(\pm{3\sigma}\)の範囲に収まる確率は99.7%である
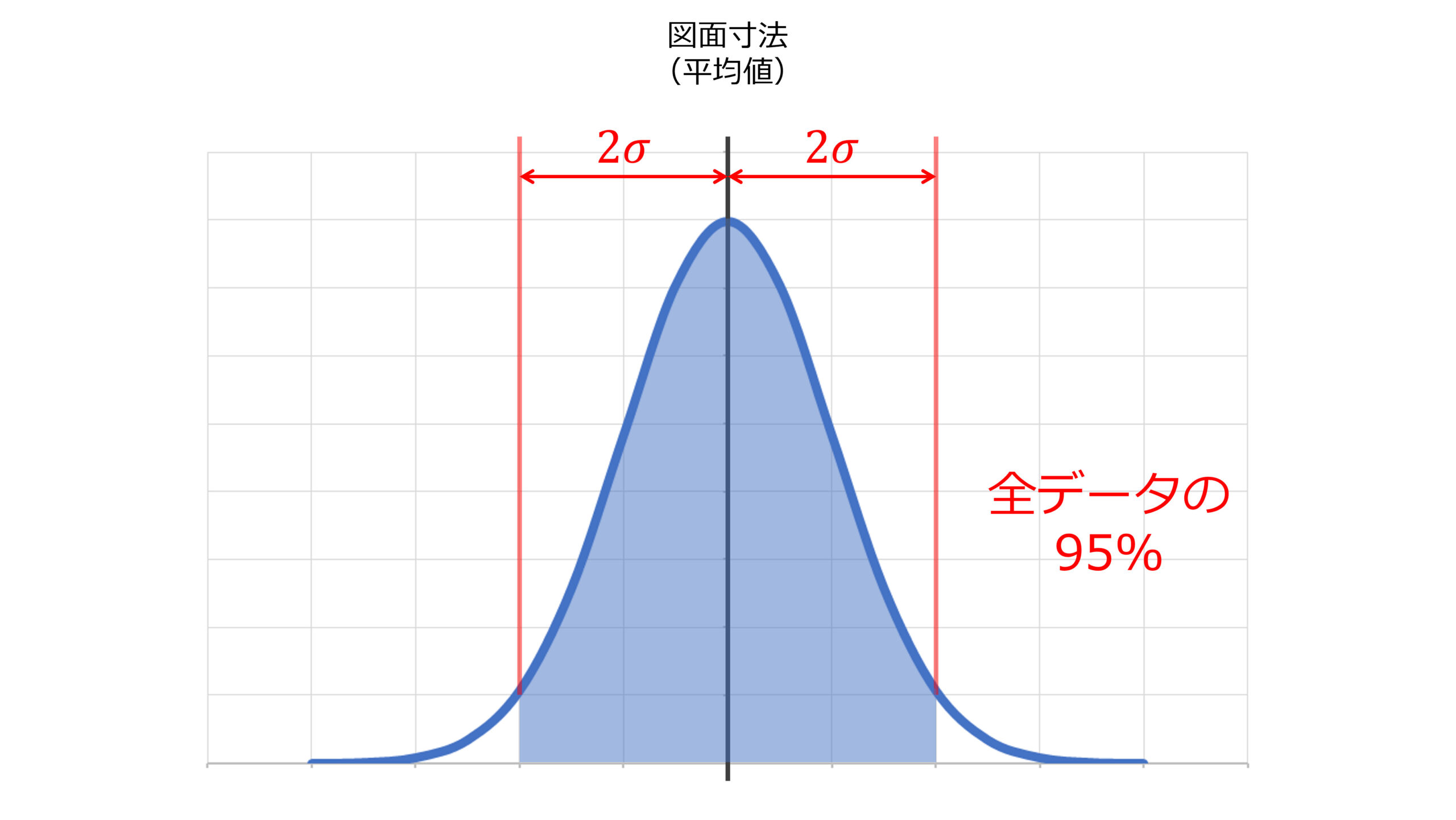
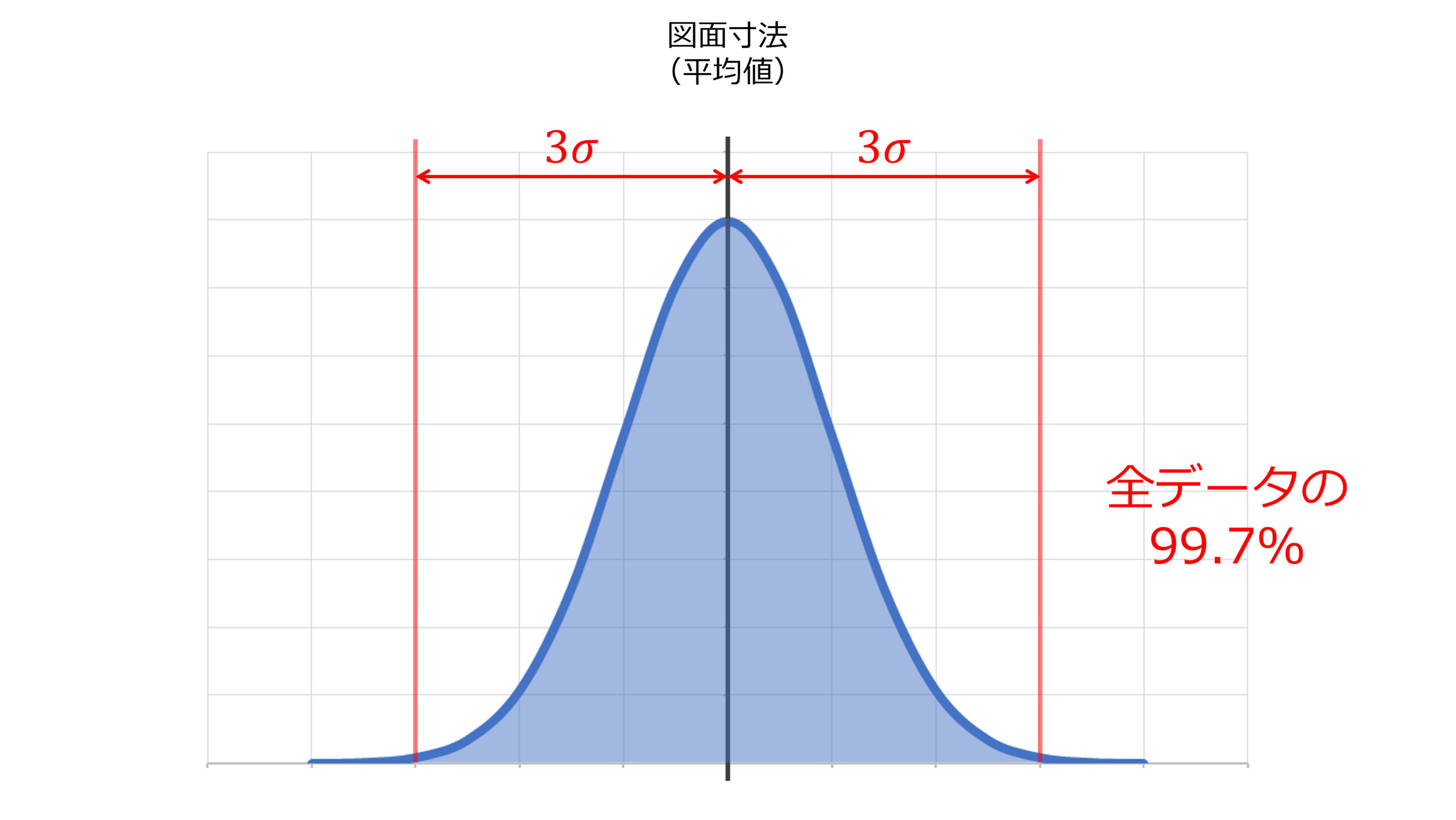
以上のことから,寸法の公差の指定には\(3\sigma\)を用いるのが妥当だとされている
設計屋さんの立場だと,標準偏差\(\sigma\)が0.5mmの加工方法を適用するときに部品の寸法に1.5mm(\(3\sigma\))の公差を設定しておけば,99.7%の部品が想定内のばらつきに収まるということである
部品屋さんの立場だと,公差(\(3\sigma\))が1mmの部品を作るときには標準偏差\(\sigma\)が0.33mmになるように製造方法を考えれば,良品率99.7%の部品を納品することができるということである
ちなみに,\(\pm{\sigma}\)の範囲は偏差値でいうと40~60に相当し,\(\pm{2\sigma}\)の範囲は偏差値30~70,\(\pm{3\sigma}\)の範囲は偏差値20~80に相当する
偏差値は以下の式で表される
\begin{equation}
\frac{x_{i}-\mu}{\sigma}\times10+50
\end{equation}
偏差が\(3\sigma\)のとき,\(x_{i}=\mu+3\sigma\)なので,偏差値は80になる
\begin{equation}
\frac{\left(\mu+3\sigma\right)-\mu}{\sigma}\times10+50=3\times10+50=80
\end{equation}
文科省が公開している日本人男性17歳の身長の分布は平均170.8㎝/標準偏差5.9㎝の正規分布にほぼ従うので,\(\pm{3\sigma}\)は身長153.1㎝~188.5㎝に相当する
日本人男性の体形に合わせた製品を作るときには身長153.1cm~188.5cmを想定しておけばだいたい問題なさそう,というのは直感的に同意できるんじゃないだろうか

組立品の公差は二乗和平方根で計算できる
公差を\(3\sigma\)に設定することで,99.7%の部品は公差の範囲内に収まることが分かった
公差を持った部品を組み合わせてできる組立品の公差\(\left(3\sigma\right)_{assy}\)は,それぞれの部品の公差\(\left(3\sigma\right)_{i}\)が独立である場合,部品の公差の二乗和平方根で計算できる
\begin{equation}
\left(3\sigma\right)_{assy}=\sqrt{\left(3\sigma\right)_{1}^2+\left(3\sigma\right)_{2}^2+\left(3\sigma\right)_{3}^2+\cdots}
\end{equation}
「部品の公差が独立である」というのは,同じラインで同じ工具で作られている場合は似たようなばらつきが出る可能性が高いのでこの計算方法が適用できない,という意味である
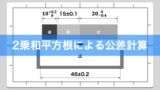
例えば,下の図のような組立品の公差は,次のように計算できる
\begin{equation}
20+30+50\pm{\sqrt{0.2^{2}+0.5^{2}+1.0^{2}}}=100\pm{1.13578166916}\simeq100\pm{1.14}
\end{equation}
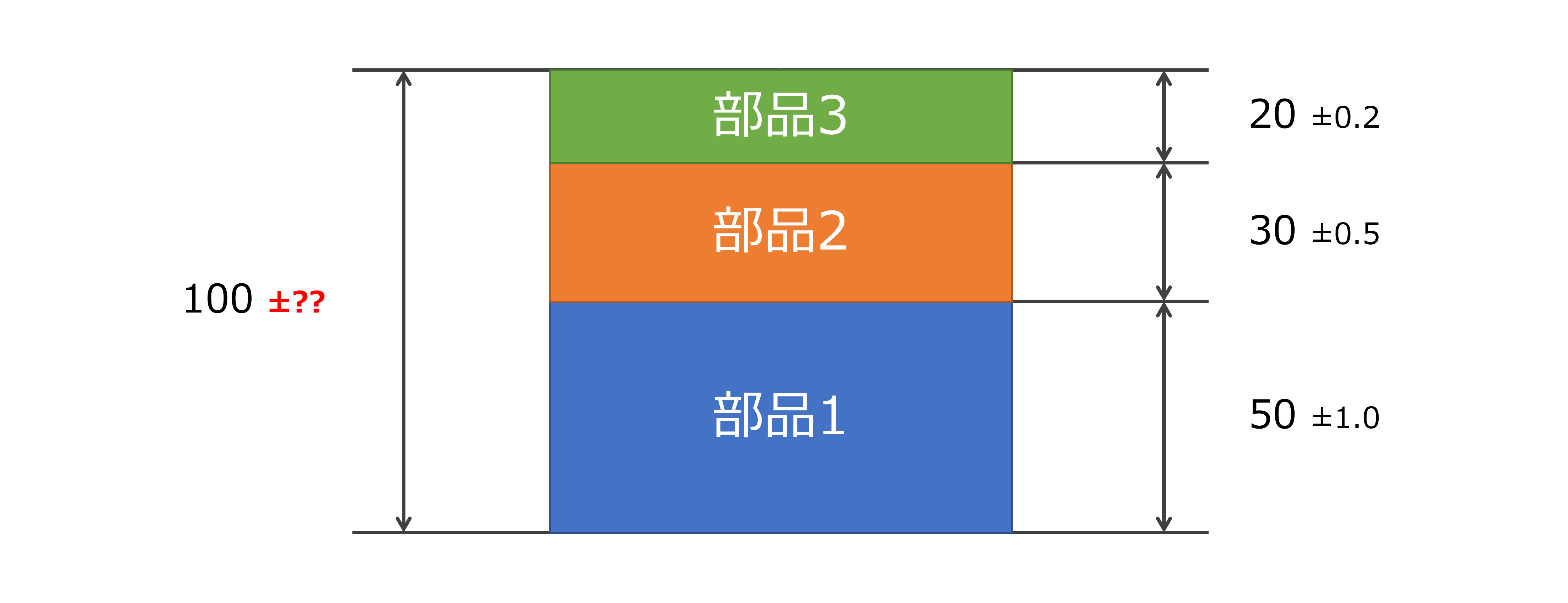
つまり,上図の部品1~3を組み合わせた組立品の寸法は,99.7%の確率で98.86mm~101.14mmの範囲に収まるということである
部品の公差を単純に足し合わせると100±1.7mm(98.3mm~101.7mm)なので,二乗和平方根を用いることで余分な設計マージンを排除できていることが分かる
組立品の公差は,分散の加法性により計算できる
分散\(\sigma^2\)は,それぞれの分散が独立な場合,次のように単純に足し算ができる
\begin{equation}
\sigma_{X+Y}^2=\sigma_{X}^2+\sigma_{Y}^2
\end{equation}
分散の加法性を用いると,組立品の分散\(\sigma_{assy}^2\)はそれぞれの部品の分散\(\sigma_{i}^2\)の線形和で表される
\begin{equation}
\sigma_{assy}^2=\sigma_{1}^2+\sigma_{2}^2+\sigma_{3}^2+\cdots
\end{equation}
公差は標準偏差の3倍(\(3\sigma\))なので,上式の両辺を9倍する
\begin{align}
9\sigma_{assy}^2&=&9\sigma_{1}^2+9\sigma_{2}^2+9\sigma_{3}^2+\cdots\\\\
\left(3\sigma_{assy}\right)^2&=&\left(3\sigma_{1}\right)^2+\left(3\sigma_{2}\right)^2+\left(3\sigma_{3}\right)^2+\cdots\\
\end{align}
両辺の平方根を取ると「組立品の公差\(\left(3\sigma\right)_{assy}\)はそれぞれの部品の公差\(\left(3\sigma\right)_{i}\)の2乗和平方根で計算できる」が証明できる
\begin{align}
\left(3\sigma\right)_{assy}&=&\sqrt{\left(3\sigma\right)_{1}^2+\left(3\sigma\right)_{2}^2+\left(3\sigma\right)_{3}^2+\cdots}\\
\end{align}
分散\(\sigma^2\)は,それぞれの分散が独立な場合,次のように単純に足し算ができる
\begin{equation}
\sigma_{X+Y}^2=\sigma_{X}^2+\sigma_{Y}^2
\end{equation}
上式で表される分散の加法性を証明する
分散は,偏差の二乗の平均値として計算できる
\begin{equation}
\sigma^2=\frac{\sum{\left(x_{i}-\mu\right)^2}}{n}
\end{equation}
この定義を用いると,XとYの合計の分散\(\sigma_{X+Y}^2\)は以下のようになる
\begin{equation}
\sigma_{X+Y}^2=\frac{\sum{\left\{\left(x_{i}+y_{i}\right)-\left(\mu_{x}+\mu_{y}\right)\right\}^2}}{n}
\end{equation}
結論ありきで展開していく
\begin{align}
&\sigma_{X+Y}^2=\frac{\sum{\left(
x_{i}^2+2x_{i}y_{i}+y_{i}^2
+\mu_{x}^2+2\mu_{x}\mu_{y}+\mu_{y}^2
-2x_{i}\mu_{x}-2x_{i}\mu_{y}-2y_{i}\mu_{x}-2y_{i}\mu_{y}
\right)}}{n}\\\\
&\sigma_{X+Y}^2=\frac{\sum{\left\{
\left(x_{i}-\mu_{x}\right)^2+\left(y_{i}-\mu_{y}\right)^2
+2x_{i}y_{i}+2\mu_{x}\mu_{y}-2x_{i}\mu_{y}-2y_{i}\mu_{x}
\right\}}}{n}\\\\
&\sigma_{X+Y}^2=\frac{\sum{\left\{
\left(x_{i}-\mu_{x}\right)^2+\left(y_{i}-\mu_{y}\right)^2
+2\left(x_{i}-\mu_{x}\right)\left(y_{i}-\mu_{y}\right)
\right\}}}{n}\\\\
&\sigma_{X+Y}^2=
\frac{\sum{\left(x_{i}-\mu_{x}\right)^2}}{n}
+\frac{\sum{\left(y_{i}-\mu_{y}\right)^2}}{n}
+\frac{\sum{2\left(x_{i}-\mu_{x}\right)\left(y_{i}-\mu_{y}\right)}}{n}
\end{align}
よって,XとYの合計の分散\(\sigma_{X+Y}^2\)は次の式で表される
\begin{equation}
\sigma_{X+Y}^2=\sigma_{X}^2+\sigma_{Y}^2+\sigma_{XY}^2
\end{equation}
ここで,\(\sigma_{XY}^2\)は共分散とよばれる値で,XとYのばらつきの相関をあらわす値である
\begin{equation}
\sigma_{XY}^2=\frac{\sum{2\left(x_{i}-\mu_{x}\right)\left(y_{i}-\mu_{y}\right)}}{n}
\end{equation}
XとYの相関の大きさを表す相関係数\(r\)は次の式で計算できる
\begin{equation}
r=\frac{\sigma_{XY}}{\sigma_{X}\sigma_{Y}}
\end{equation}
上式より,XとYが独立(相関係数\(r\)がゼロ)のとき,共分散\(\sigma_{XY}^2\)の値がゼロであることが分かる
以上より,XとYが独立のとき,分散の加法性が成立することが証明できた
\begin{equation}
\sigma_{X+Y}^2=\sigma_{X}^2+\sigma_{Y}^2
\end{equation}
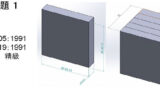
また,以下の例のように,ある部品の寸法が組立品の寸法の差で計算される場合も,公差については2乗和平方根を取ればよい
\begin{equation}
100-20\pm{\sqrt{1.0^{2}+0.5^{2}}}=80\pm{1.11803398875}\simeq80\pm{1.12}
\end{equation}
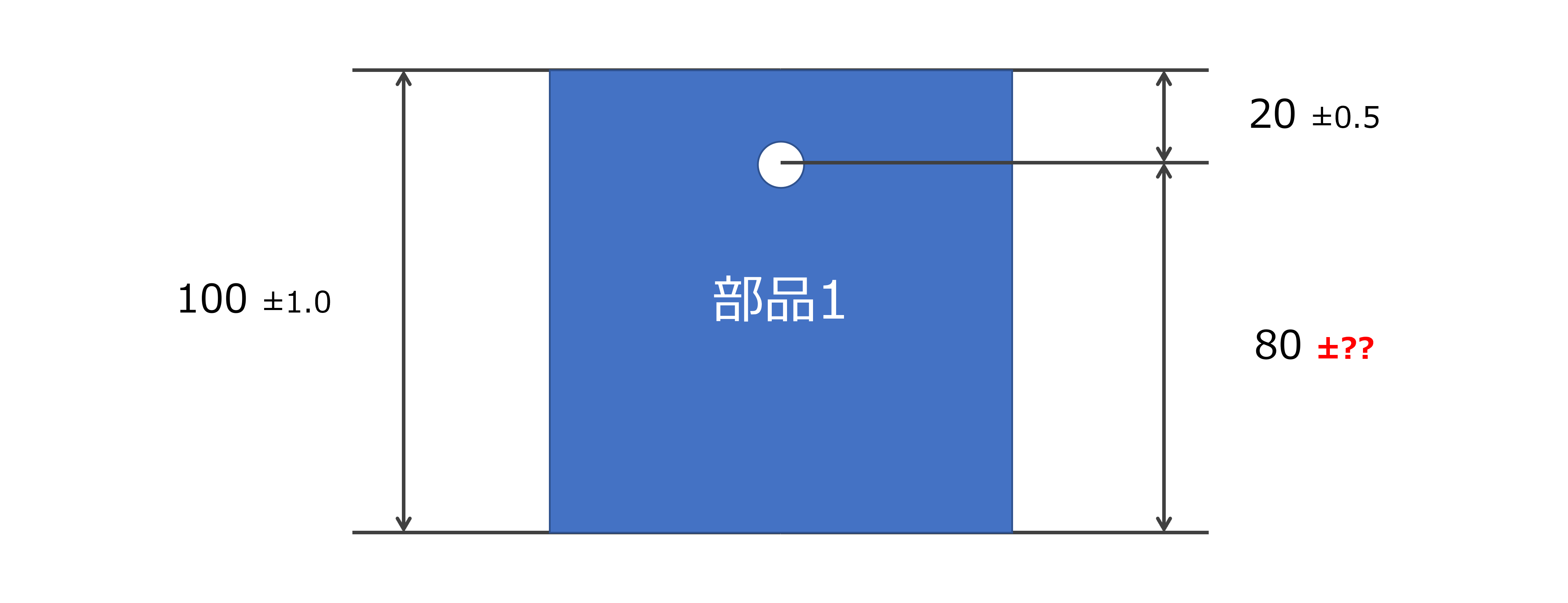
上部品における穴位置は,99.7%の確率で78.88mm~81.12mmの範囲に収まることになる
おわりに
寸法のばらつきを理解し,公差の集積を計算するための方法について説明した
- 部品にはばらつきが存在する
- ばらつきとは統計学でいうところの標準偏差である
- 公差は標準偏差の3倍として設定される
- 組立品の公差は部品それぞれの公差の2乗和平方根で計算できる







コメント
「ある部品の公差が組立品の公差を減らす方向に作用する場合は,2乗和平方根を取るときの符号をマイナスにする」
の所が分かりません。公差は足すものと思っていました。
仮に100の公差が±0.5、20が±0.5だった場合、穴位置である80の公差はゼロになるということですか?
コメントいただきありがとうございます。
私の理解に誤りがありました。
ご指摘いただいた通り「公差は足すもの」なので、記事の記述を修正いたしました。
80±0.86602540378≃80±1.12の所が間違っていますね。
80±1.11803398874989です。
度々ありがとうございます。
修正いたしました。