OpenFOAMにおけるLESのbox filterの実装について説明する
ソースコードはGithubを参照
≫mtkbirdman.com/OpenFOAM/
キーワード:LES filter, box filter, implementation
はじめに
OpenFOAMで,LESのbox filterを実装する
実装するfilterは以下の論文に出てくるfiltering operator
we adopt a box-type (volume-averaging-type) filtering operator, in which the filter width is twice as wide as the local grid spacing.
C言語については以下のサイトがおすすめ
≫苦しんで覚えるC言語 - 苦しんで覚えるC言語
C++は次のサイトを読んで完全に理解した
≫C++入門
このfiltering operatorを使った乱流モデルの実装はこちら
≫【OpenFOAM v2006】非線形SGSモデルの実装
概要
フィルター幅\({\hat \Delta}=2\Delta\)のbox-averaging-type filtering operatorは,対象のセルと隣接セルの体積が等しいという仮定の下に以下のように定式化する
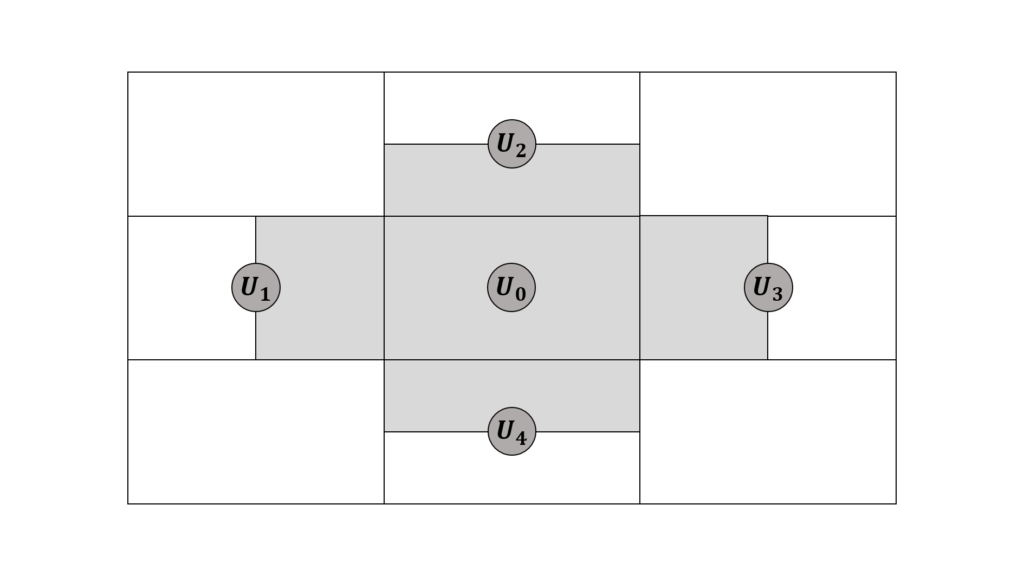
隣接セルの個数が6個の構造格子ならこんな感じ
\begin{eqnarray}
{\overline U}&=&\frac{U_{0}+0.5\times\left(U_{1}+\ldots+U_{6}\right)}{1+0.5\times6}
=\frac{2U_{0}+U_{1}+\ldots+U_{6}}{8} \tag{1}
\end{eqnarray}
隣接セルの個数が\(n\)個の非構造格子ならこんな感じ
\begin{eqnarray}
{\overline U}&=&\frac{U_{0}+0.5\sum_{i}^{n} U_{i}}{1+0.5n} \tag{2}
\end{eqnarray}
実装
ベースモデルのコピー
次のコマンドをたたいてsimpleFilterを$WM_PROJECT_USER_DIR/src/myTurbulenceModelsにコピーする
>> cp -r $WM_PROJECT_DIR/src/TurbulenceModels/turbulenceModels/LES/LESfilters/simpleFilter $WM_PROJECT_USER_DIR/src/myTurbulenceModels次のコマンドで,乱流モデルの名前をsimpleFilterからboxFilterに変更する
>> cd $WM_PROJECT_USER_DIR/src/myTurbulenceModels/
>> mv simpleFilter boxFilter
>> cd boxFilter
>> mv simpleFilter.H boxFilter.H
>> mv simpleFilter.C boxFilter.C
>> sed -i -e "s/simpleFilter/boxFilter/g" boxFilter.*プログラムの変更
boxFilter.H
boxFilter.HのコードはGithubのコードを参照
≫mtkbirdman.com/OpenFOAM/src/myTurbulenceModels/boxFilter/boxFilter.H
注意点は以下の通り
TypeName("simple");は上のコマンドでは変更されないので手動でTypeName("box");に変更する
boxFilter.C
boxFilter.CのコードはGithubのコードを参照
≫mtkbirdman.com/OpenFOAM/src/myTurbulenceModels/boxFilter/boxFilter.C
重要な点のみ説明する
volVectorFieldのフィルターのoperator()
volScalarFieldでもvolSymmTensorFieldでもコードはほとんど変わらない
Foam::tmp<Foam::volVectorField> Foam::boxFilter::operator()
(
const tmp<volVectorField>& unFilteredField
) const
{
correctBoundaryConditions(unFilteredField);
volScalarField neighbors(fvc::surfaceSum(mesh().magSf()/mesh().magSf()));
tmp<volVectorField> filteredField = (unFilteredField*(scalar(1) - widthCoeff_*neighbors) + fvc::surfaceSum(fvc::interpolate(unFilteredField)))/(scalar(1) + widthCoeff_*neighbors);
unFilteredField.clear();
return filteredField;
}使うのはfvc::surfaceSumとfvc::interpolateの2つでOpenFOAM® DocumentationのProgrammer’s Guideで以下のように説明されている
Surface sum
fvc::surfaceSum performs a summation of surfaceField face values bounding each cell, i.e. \(\sum_{f} \phi_{f}\) returning a volField.Face interpolate
Programmer’s Guide Download PDF
The geometricField function faceInterpolate() interpolates volField cell centre values to cell faces using central differencing, returning a surfaceField.
filteredField \(={\hat U}\),unFilteredField \(=U\)とすると,対象のセルと隣接セルの体積が等しいという仮定の下ではセル表面上の値(surfaceScalarField)は次のようになる(と考えられる)
fvc::interpolate(unFilteredField) \(\simeq\frac{U_{0}+U_{i}}{2}\)
これに対してfvc::surfaceSumをとると次のvol<type>Fieldが返ってくる
fvc::surfaceSum(fvc::interpolate(unFilteredField))
\(\qquad \simeq\sum_{i}^{n}\frac{U_{0}+U_{i}}{2}=\frac{U_{0}\times n+\sum_{i}^{n}U_{i}}{2}=0.5n\times U_{0}+0.5\sum_{i}^{n}U_{i}\)
また,隣接するセルの数\(n\)は次のようにして求めた
\(\quad n=\) fvc::surfaceSum(mesh().magSf()/mesh().magSf())
mesh().magSf()はセル表面上でその面の面積を値に持つsurfaceScalarFieldで,mesh().magSf()/mesh().magSf()によってセル表面上で1.0の値を持つsurfaceScalarFieldを得ることができる
これにfvc::surfaceSumをかけると,隣接するセルの数の値\(n\)を持つvolScalarFieldが手に入る
あとは上の式(2)を実装すればいい
tmp<volTensorField> filteredField = (unFilteredField*(scalar(1) - widthCoeff_*neighbors) + fvc::surfaceSum(fvc::interpolate(unFilteredField)))/(scalar(1) + widthCoeff_*neighbors);コンパイル・計算・結果
親記事(≫【OpenFOAM v2006】非線形SGSモデルの実装)を参考
まとめ
最初はforAllとmesh.cellCells()を使って実装しようとしたが,メモリのエラーが出てうまくいかなかった
fvc::interpolate()でも同じことができるということに気づけて良かった
box filterの実装の情報はどこにもなかったのでどこかの誰かの参考になればうれしい
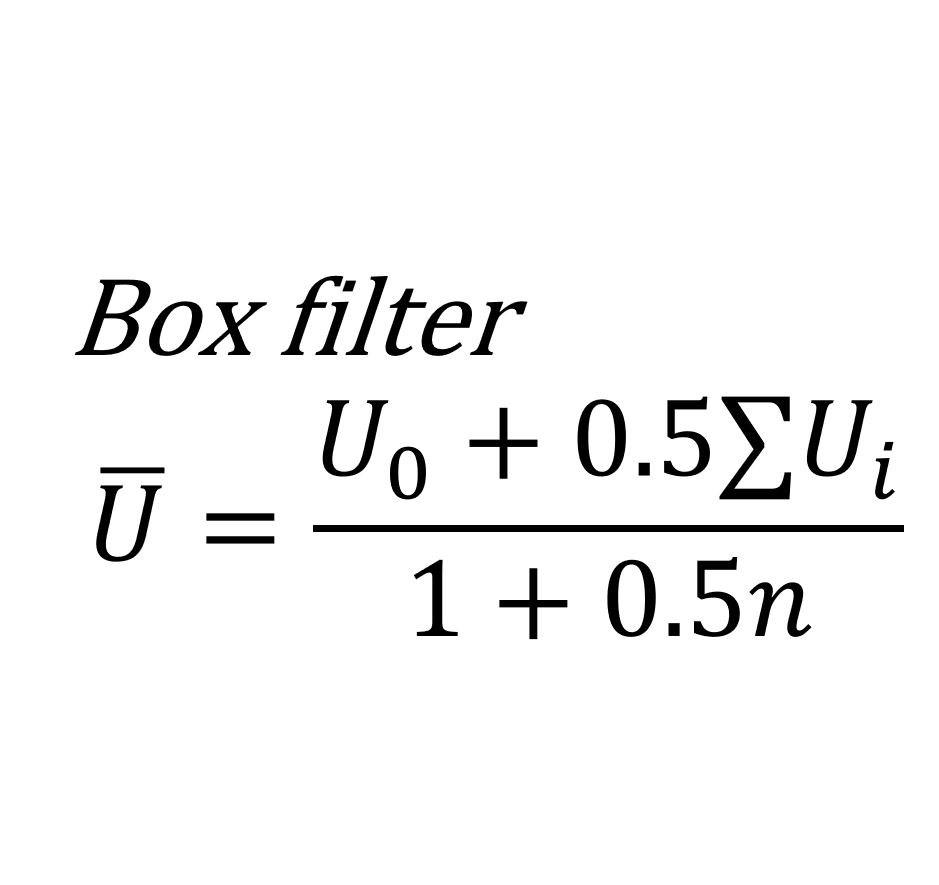


コメント