OpenFOAMにおけるLESの非線形SGSモデルの実装について説明する
計算に使ったファイルはGithubにアップしてある
≫mtkbirdman.com/OpenFOAM/
キーワード:channel395, mapFields, LES, チャネル乱流, scale similarity model, anisotoropic SGS model
はじめに
OpenFOAMで,LESの非線形SGSモデルを実装する
実装するモデルは以下の論文の"Stabilized Mixed Mode (SMM)"
乱流モデルの詳細な説明は論文に譲るが,SGS応力に非線形項を加えることでLESの格子依存性を大幅に改善した1方程式のSGSモデルである
計算のケースについては以下の論文を参考
C言語については以下のサイトがおすすめ
≫苦しんで覚えるC言語 - 苦しんで覚えるC言語
C++は次のサイトを読んで完全に理解した
≫C++入門
非線形RANSモデルを実装したときの記事はこちら
≫【OpenFOAM v2006】低Re数型非線形RANSモデルの実装
概要
1方程式の非線形SGSモデルを実装するので,
- 1方程式LESモデル→
kEqn - 非線形(RANS)モデル→
LienCubicKE
のプログラムを参考にしながら修正を加えていく
また,論文で使われている\(\Delta\)やfiltering operationもOpenFOAMでは実装されていないので,新たに実装する必要がある
実装
ベースモデルのコピー
次のコマンドをたたいてkEqnを$WM_PROJECT_USER_DIR/src/myTurbulenceModelsにコピーする
>> cp -r $WM_PROJECT_DIR/src/TurbulenceModels/turbulenceModels/LES/kEqn $WM_PROJECT_USER_DIR/src/myTurbulenceModels次のコマンドで,乱流モデルの名前をkEqnからSMMに変更する
>> cd $WM_PROJECT_USER_DIR/src/myTurbulenceModels/
>> mv kEqn SMM
>> cd SMM
>> mv kEqn.H SMM.H
>> mv kEqn.C SMM.C
>> sed -i -e "s/kEqn/SMM/g" SMM.*プログラムの変更
OpenFOAMはC++で書かれているので,オブジェクト指向が使われている
そのため,クラスの継承をうまく使えば非線形RANSモデルのときのように末端のファイルを書き換えるだけでいい
Class Reference
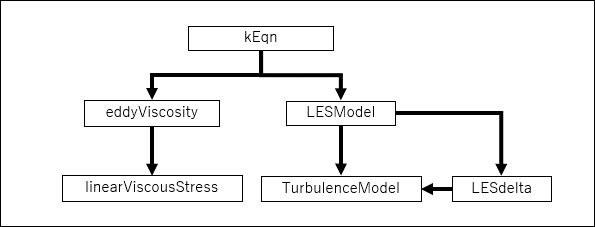
kEqnのClass Referenceは以下のようになっている
≫kEqn.H File Reference
LienCubicKEのClass Referenceは以下のようになっている
≫LienCubicKE.H File Reference
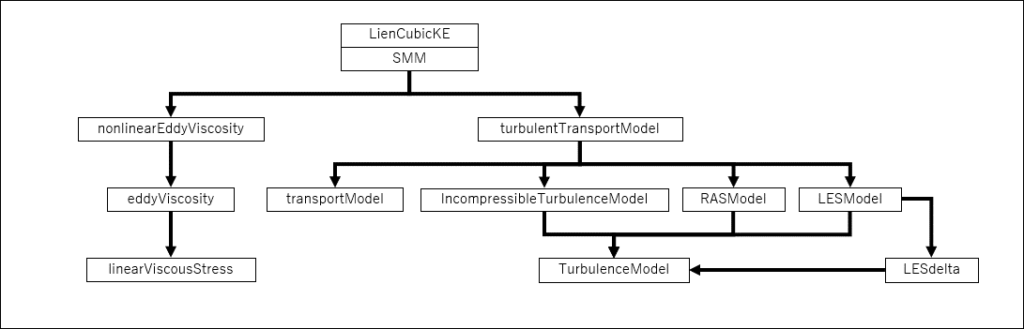
注目してほしいのは,LienCubicKEのClass Referenceの中に,kEqnのClass Referenceに含まれているクラスがすべて含まれていることである
このおかげで,LESの非線形モデルの実装はLienCubicKEと同じClass Referenceを使えば比較的容易に行うことができる
SMM.H
SMM.HのコードはGithubのコードを参照
≫mtkbirdman.com/OpenFOAM/src/myTurbulenceModels/SMM/SMM.H
変更点はだいたい以下の通り
LienCubicKEのRASModelsをLESModelsに変更epsilonの輸送方程式を削除volScalarField LESDelta_を追加(\(\Delta\)の値を出力するため)- その他もろもろ
SMM.C
SMM.Cのコードの重要な部分を説明する
コード全体はGithubのコードを参照
≫mtkbirdman.com/OpenFOAM/src/myTurbulenceModels/SMM/SMM.C
式番号は実際の論文に合わせてある
\(f_{SGS}\)
tmp<volScalarField> SMM::fSGS() const
{
const volScalarField epsilon_(Ce_*k_*sqrt(k_)/delta() + 2.0*nu()*k_/sqr(y_)); //eq.(12)
const volScalarField uEps_(pow(nu()*epsilon_,1.0/4.0)); //eq.(11)
const volScalarField yEps_(((uEps_*y_)/nu())*sqrt((Cl_*y_)/delta())); //eq.(11)
return scalar(1)-exp(-pow(yEps_/A0_,4.0/3.0)); //(eq.10)
}\(\varepsilon_{SGS}\).ここで定義した関数epsilon()はここ以外で全く使わない
tmp<volScalarField> SMM::epsilon() const
{
return tmp<volScalarField>
(
new volScalarField
(
IOobject
(
IOobject::groupName("epsilon", this->alphaRhoPhi_.group()),
runTime_.timeName(),
mesh_,
IOobject::NO_READ,
IOobject::AUTO_WRITE
),
Ce_*k_*sqrt(k_)/delta() + 2.0*nu()*k_/sqr(y_) //eq.(12)
)
);
}\(\nu_{t}\)と\(\tau_{ij}\)の非線形項\(2k_{SGS}b_{ij}\)
void SMM::correctNonlinearStress(const volTensorField& gradU)
{
nut_ = CSGS_*fSGS()*sqrt(k_)*delta(); //eq.(10)
nut_.correctBoundaryConditions();
dimensionedScalar smallValue1("smallValue1",dimensionSet(0,0,-2,0,0,0,0),SMALL);
dimensionedScalar smallValue2("smallValue2",dimensionSet(0,2,-2,0,0,0,0),SMALL);
volVectorField UHat_(filter_(U_));
volSymmTensorField TauPrime(CB_*symm((U_ - UHat_)*(U_ - UHat_))); //eq.(4)
volSymmTensorField TauPrimeA(dev(TauPrime));
volSymmTensorField S(symm(gradU)); //eq.(2)
volScalarField nuPrime(-(TauPrimeA && S)/(2.0*max(magSqr(S),smallValue1))); //eq.(5)
nonlinearStress_ = 2.0*k_*(TauPrimeA - (-2.0*nuPrime*S))/max(tr(TauPrime),smallValue2); //eq.(9)
}ゼロ割を防ぐためにsmallValue1とsmallValue1を定義している
乱流エネルギー\(k_{SGS}\)の輸送方程式
void SMM::correct()
{
if (!turbulence_)
{
return;
}
nonlinearEddyViscosity<incompressible::LESModel>::correct();
tmp<volTensorField> tgradU(fvc::grad(U_));
const volTensorField& gradU = tgradU();
volScalarField divU(fvc::div(fvc::absolute(phi_, U_)));
volScalarField G(GName(), (nut_*dev(twoSymm(gradU)) - nonlinearStress_) && gradU);
tmp<fvScalarMatrix> kEqn //eq.(13)
(
fvm::ddt(k_) //Dk/dt
+ fvm::div(phi_, k_) //Dk/dt
- fvm::laplacian(nu() + Ck_*fSGS()*sqrt(k_)*delta(), k_) //d/dxj(nu+Ck*fsgs*sqrt(k)*delta)dk/dxj)
==
G //tauij*dUi/dxj
- fvm::SuSp((2.0/3.0)*divU, k_) //tauij*dUi/dxj
- fvm::Sp(Ce_*sqrt(k_)/delta() + 2.0*nu()/sqr(y_), k_) //epsilon
);
kEqn.ref().relax();
solve(kEqn);
bound(k_, kMin_);
correctNonlinearStress(gradU);
}LESのモデルとRANSのモデルでプログラマーが違うのか,2つのモデルで表記ゆれがある
例えば
- thisポインタの有無
- 輸送方程式の
- fvm::SuSp((2.0/3.0)*divU, k_)の項の有無 - SGS応力の線形項の
dev( )の有無
などである.2つ目と3つ目に関しては連続の式よりどちらも数式的には変わらない
プログラム中で使われているsymm,dev,magSqr,trなどのTensor operationや,fvm::ddt,fvm::div,fvm::laplacianなどの演算子は,OpenFOAMの公式ドキュメントであるProgrammer's Guideに定義が記載されている
≫OpenFOAM® Documentation
LESdelta
次の\(\Delta\)を実装する
\begin{eqnarray}
\Delta=\sqrt{the~maximum~area~among~the~faces~of~a~cell} \tag{14}
\end{eqnarray}
詳しくは以下の記事を参考
≫【OpenFOAM v2006】LES deltaの実装
LESfilter
フィルター幅\({\hat \Delta}=2\Delta\)のbox-type (volume-averaging-type) filtering operationを実装する
詳しくは以下の記事を参考
≫【OpenFOAM v2006】box filterの実装
コンパイル
乱流モデルを実装したのでコンパイルを行う
Make/files
SMM/SMM.C
maxSqrtFaceDelta/maxSqrtFaceDelta.C
boxFilter/boxFilter.C
LIB = $(FOAM_USER_LIBBIN)/libmyTurbulenceModelsMake/options
EXE_INC = \
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude \
-I$(LIB_SRC)/fvOptions/lnInclude \
-I$(LIB_SRC)/transportModels \
-I$(LIB_SRC)/TurbulenceModels/turbulenceModels/lnInclude \
-I$(LIB_SRC)/TurbulenceModels/incompressible/lnInclude \
LIB_LIBS = \
-lincompressibleTransportModels \
-lincompressibleTurbulenceModels \
-lturbulenceModels \
-lfvOptions \
-lfiniteVolume \
-lmeshTools2つのファイルを$WM_PROJECT_USER_DIR/src/myTurbulenceModelsに用意し,以下のコマンドでコンパイルを行う
>> wmake libso計算の実行
ケースはtutorial/channel395をベースにちょこちょこいじったもの
Case directoryの詳細はGithubのコードを参照
≫mtkbirdman.com/OpenFOAM/C395E/
概要は以下の通り
| Model | Channel flow |
| Solver | pimpleFOAM |
| Turbulence Model | SMM |
| \(Re_{\tau}\) | 395 |
| Dimensions | (x, y, z)=(6.4, 2,0, 3.2) [m] |
| Nodes | (32, 64, 32) → C395E |
| Mesher | blockMesh |
| endTime | 1e+2 [s] |
| \(\Delta t\) | 1e-3 [s] |
計算に使用したノートPCの性能は以下の通りで,上の計算を行うのに約10時間かかった
| OS | Window 10 Home 64bit |
| CPU | intel(R) CORE(TM) i5-8250U @ 1.60GHz |
| コア数 | 4 |
| クロック周波数 | 1.80 GHz |
| メモリ | 8.00 GB |
| ストレージ | SSD 256 GB |
ちなみにtutorial/channel395の初期条件を格子サイズを変更して使いまわすには,mapFieldsというutilityを使用する
≫PENGUINITIS - データのマッピング
ポスト処理
論文と同じような図を描くためには,それぞれの物理量の時間平均+空間平均をとる必要がある
そのためのpythonプログラムpostChannel.pyがこれ
import os
import numpy as np
import csv
def rawToNumpy(filepath,filename,Nx=32,Ny=48,Nz=32,Cy=False,T=False,Tsymm=False):
PATH = os.path.join(filepath, filename)
print(PATH)
with open(PATH, "r") as f:
data = f.readlines()
data = [line.strip().strip('(').strip(')').replace(' ',',').split(',') for line in data]
datasize = int(data[21][0])
data = np.array(data[23:datasize+23],dtype='float64')
data1 = data[0:int(data.shape[0]/2),:].reshape(Nx,Ny,Nz,-1)
data2 = np.flip(data[int(data.shape[0]/2):int(data.shape[0]),:].reshape(Nx,Ny,Nz,-1),axis=1)
if T:
for n in [1,2,3,6]:
data2[:,:,:,n] = -data2[:,:,:,n]
if Tsymm:
for n in [1,2]:
data2[:,:,:,n] = -data2[:,:,:,n]
data = 0.5*(data1+data2)
if Cy:
data = 0.5*(data1+(2-data2))
return data
PATH = "./100"
turbName = "turbulenceProperties:"
Cx = rawToNumpy(PATH,"Cx")
Cy = rawToNumpy(PATH,"Cy",Cy=True)
Cz = rawToNumpy(PATH,"Cz")
UMean = rawToNumpy(PATH,"UMean")
pMean = rawToNumpy(PATH,"pMean")
nut = rawToNumpy(PATH,"nut")
UPrime2Mean = rawToNumpy(PATH,"UPrime2Mean",Tsymm=True)
RMean = rawToNumpy(PATH, turbName+"RMean",Tsymm=True)
gradUMean = rawToNumpy(PATH,"gradUMean",T=True)
postChannel = np.concatenate([Cy,UMean,pMean,nut,UPrime2Mean,RMean,gradUMean],axis=3).mean(axis=0).mean(axis=1)
PATH = os.path.join("./", "postChannel.csv")
print(PATH)
with open(PATH, "w") as f:
writer = csv.writer(f)
writer.writerows(postChannel)
計算実行後に34行目のPATHを変更して,以下のコマンドで実行すればケースディレクトリにpostChannel.csvができる
>> python postChannel.py
./100/Cx
./100/Cy
./100/Cz
./100/UMean
./100/pMean
./100/nut
./100/UPrime2Mean
./100/turbulenceProperties:RMean
./100/gradUMean
./postChannel.csv
>>これをExcelファイルに貼り付ければいい
結果
可視化に使ったExcelファイルがこれ
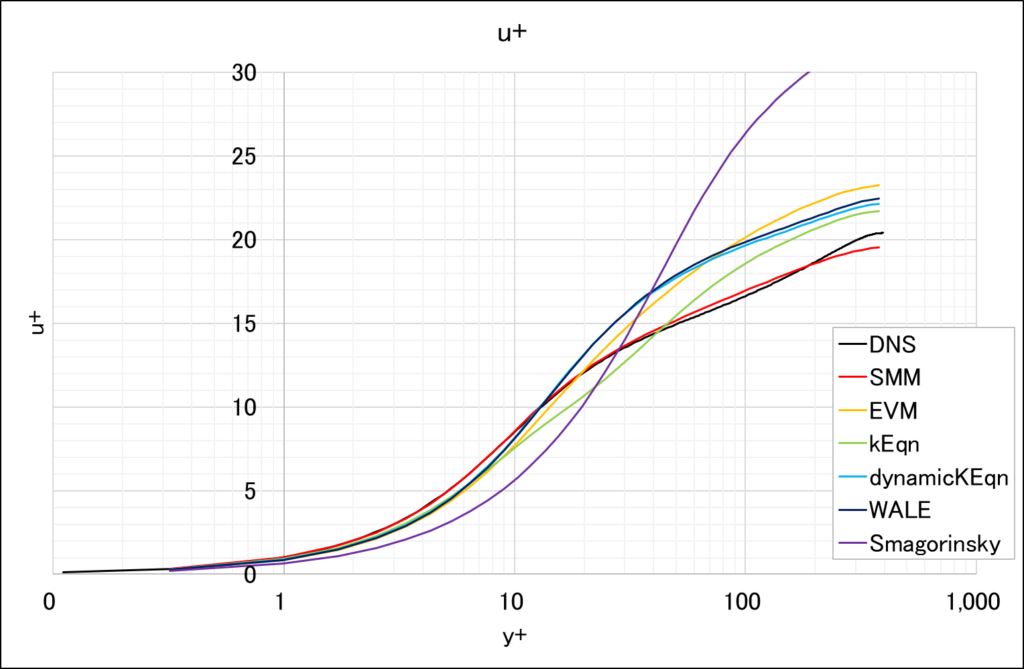
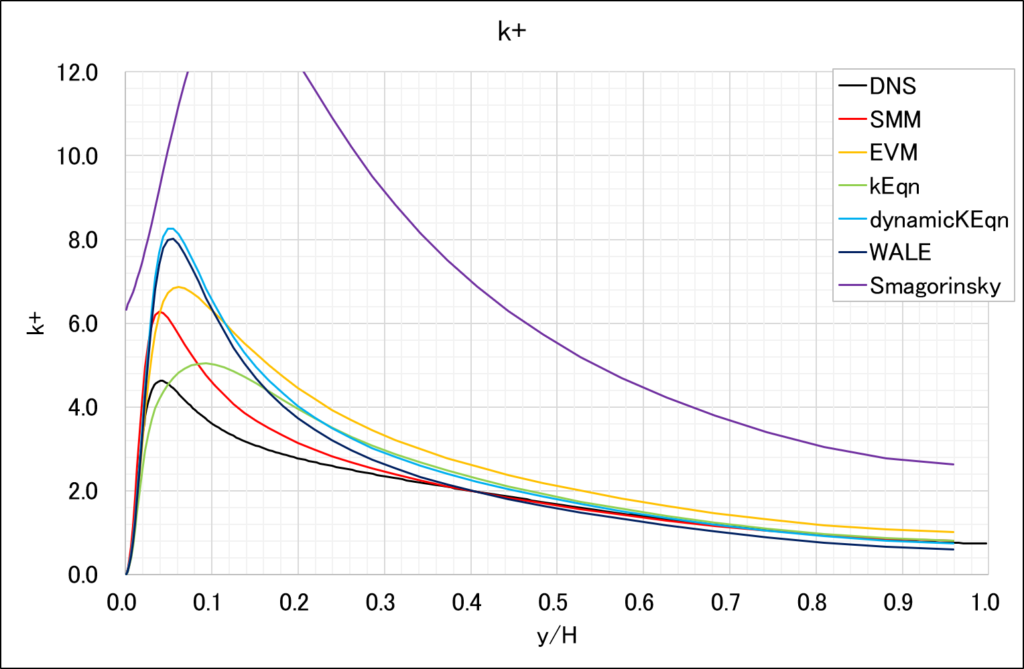
SMMの比較対象として,SMMの非線形項を0にしたモデル(EVM),OpenFOAMにデフォルトで実装されているLESのモデル,DNS Database of Wall Turbulence and Heat Transfer at Tokyo University of ScienceのPoi395_4th_D.datを用いている
また,\((~)+\)は摩擦速度\(u_{\tau}\)での無次元化を表している
以下,結果を示す
平均速度分布\(u+\)
乱流エネルギー\(k+\)
レイノルズ応力テンソル\(-uv+\)
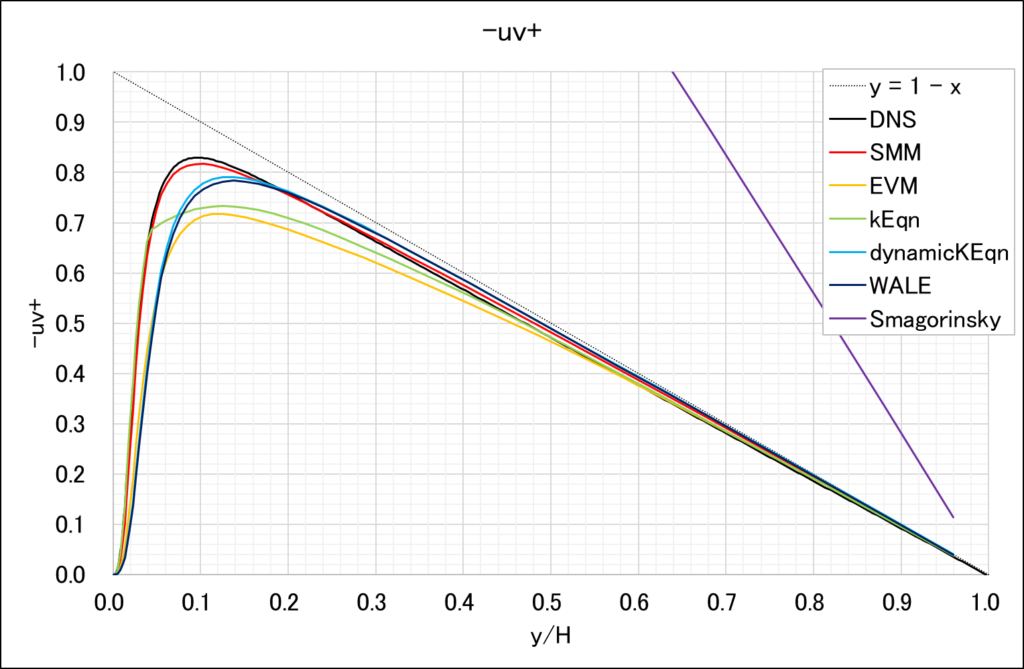
\(dx+=80\),\(dz+=40\)というLESとしてはかなり粗いグリッドにおいて,SMMは他のLESよりもDNSに近い値を予測できていることがわかる
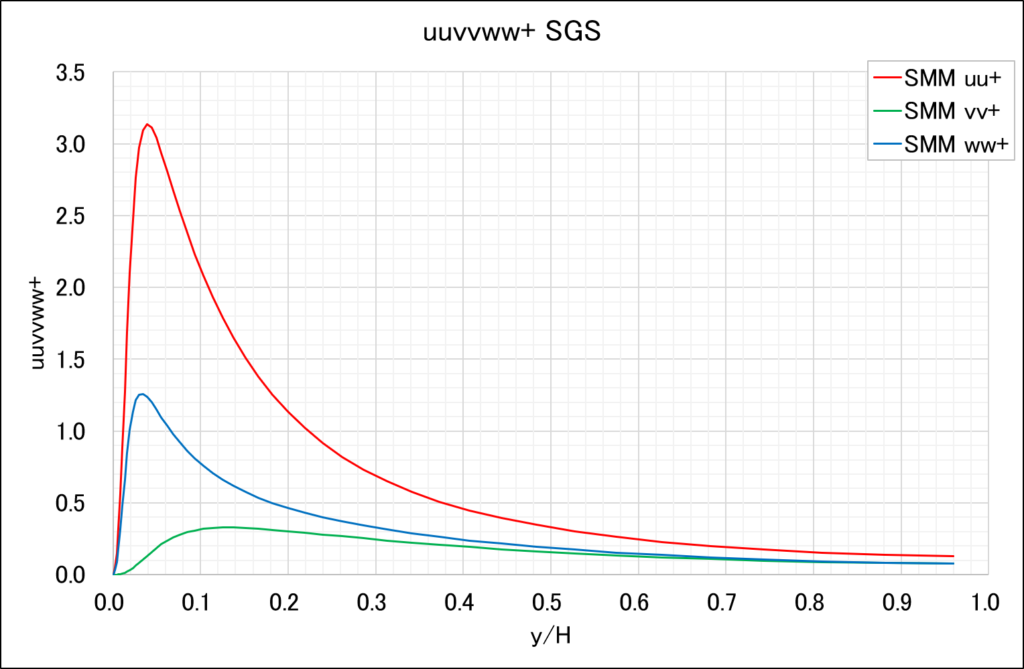
ちなみにSMMのSGS応力成分を見ると,確かに非等方になっていることが確認できる
まとめ
kEqnとLienCubicKEのClass referenceが同じだったことから非線形性の実装は比較的早く終わったが,filterとdeltaの実装にかなり時間がかかった
なにはともあれ,OpenFOAMで(もしかしたら世界初の)非線形LESモデルの実装を成し遂げることができてよかった
そのほかの乱流モデルについてはこちら



コメント