MIL-F-8785C の Short-period frequency and acceleration sensitivity をもとに,鳥コン滑空機の縦の操縦特性について考える
MIL-F-8785C
MIL規格についてのウィキペディアより
MIL規格 (ミルきかく、英: United States Military Standard) とは、一般的にアメリカ軍が必要とする様々な物資の調達に使われる規格を総称した表現である。ミルスペック(MIL-SPEC、(非公式に)MilSpecs)[1]、MIL-STD、defense standardとも呼ばれる。
フリー百科事典『ウィキペディア(Wikipedia)』
MIL-F-8785C は,航空機の飛行特性について記述している
1.1 Scope. This specification contains the requirements for the flying and handling qualities, in flight and on the ground, of U.S. Military, manned, piloted airplanes except for flight at airspeeds below Vcon (MIL-F-83300).
MIL-F-8785C p.1
Vconについてはよくわからなかったが,V/STOLのホバリング速度とかに関係ある速度っぽい
MIL-F-8785Cはこちらから
≫MIL-F-8785 C FLYING QUALITIES PILOTED AIRPLANES(オリジナル)
≫Background Information and User Guide for MIL-F-8785C, Military Specification - Flying Qualities of Piloted Airplanes(解説)
≫2011971042474.pdf(北京大学工学院がきれいなPDFにしてくれたやつ)
参考文献はいつもの通り
タイトル詐欺で有名な通称「白本」
実はMIL規格についても書いてある通称「青本」
Short-period frequency and acceleration sensitivity
今回使うのは,縦の短周期運動の非減衰固有振動数\(\omega_{n_{_{SP}}}\)についてのこの記述
3.2.2.1.1 Short-period frequency and acceleration sensitivity. The equivalent short-period undamped natural frequency, \(\omega_{n_{_{SP}}}\), shall be within the limits shown on figures 1, 2, and 3. If suitable means of directly controlling normal force are provided, the lower bounds on \(\omega_{n_{_{SP}}}\) and \(n/\alpha\) of figure 3 may be relaxed if approved by the procuring activity.
MIL-F-8785C p.13
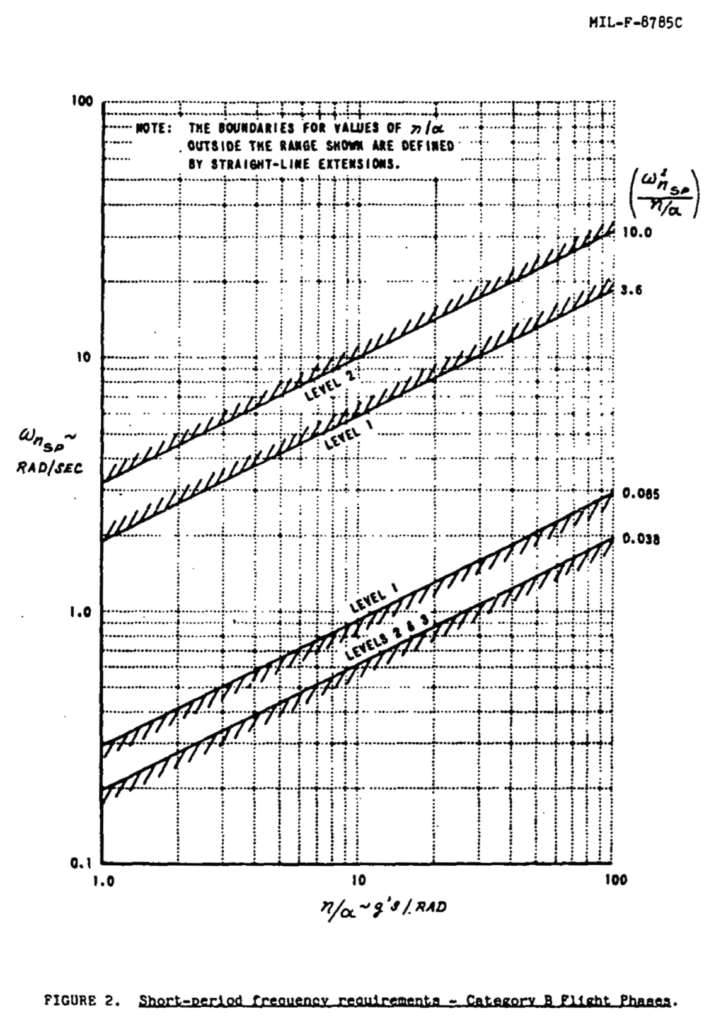
要するに,迎角\(\alpha\)が\(1 \:\mathrm{[rad]}\)変化したときの加重倍数\(n \:\mathrm{[G]}\)の変化量 \(n/\alpha \:\mathrm{[G/rad]}\)を横軸にとって,縦軸に縦の短周期運動の非減衰固有振動数\(\omega_{n_{_{SP}}} \:\mathrm{[rad/s]}\)をとったとき,設計した機体のプロットが Figure 2 の範囲内に入っていればいいということである
ちなみに,グラフのタイトルにある Category B Flight Phases とグラフの中に書いてある Level 1 と Level 2 の制限それぞれは次のように定義されている
<飛行性のレベル>
レベル1:明らかに適切な飛行性を有している.
レベル2:適切だが,任務達成に作業負担が増大し任務の効果が低下
レベル3:安全に操縦できるが,飛行作業負担が過大で任務の効果が不適切<飛行状態カテゴリ>
青本 p.57
A:急激な運動や精密な飛行経路制御を要する非発着時飛行状態.空対空戦闘もこのカテゴリであるが,運動内容によってはカテゴリCOとして特別要求を規定している項目もある.
B:上昇,巡航,降下などの緩やかな飛行状態.
C:精密な飛行経路制御を有する離着陸などの飛行状態
飛行状態のカテゴリーについて
Category B - Those nonterminal Flight Phases that are normally accomplished using gradual maneuvers and without precision tracking, although accurate flight-path control may be required. Included in this Category are:
a. Climb (CL)
MIL-F-8785C p.3
b. Cruise (CR)
c. Loiter (LO)
d. In-flight refueling (tanker) (RT)
e. Descent (D)
f. Emergency descent (ED)
g. Emergency deceleration (DE)
h. Aerial delivery (AD).
飛行性のレベルについて
1.5 Levels of flying qualities. Where possible, the requirements of section 3 have been stated in terms of three values of the stability or control parameter being specified. Each value is a minimum condition to meet one of three Levels of acceptabi9lity related to the ability to complete the operational missions for which the airplane is designed. The Levels are:
Level 1 Flying qualities clearly adequate for the mission Flight Phase
Level 2 Flying qualities adequate to accomplish the mission Flight Phase, but some increase in pilot workload or degradation in mission effectiveness, or both, exists
Level 3 Flying qualities such that the airplane can be controlled safely, but pilot workload is excessive or mission effectiveness is inadequate, or both. Category A Flight Phases can be terminated safely, and Category B and C Flight Phases can be completed.
MIL-F-8785C p.4
鳥コン滑空機のフライトがカテゴリBになるかカテゴリCになるかは微妙なところだが,今回はカテゴリBで考えることにする
計算
基本的に青本に準拠している
| 変数名 | 記号 | 単位 |
| 主翼の3次元揚力傾斜 | \(a_{w}\) | \(\mathrm{[1/deg]}\) |
| 水平尾翼の3次元揚力傾斜 | \(\alpha_{0}\) | \(\mathrm{[1/deg]}\) |
| MAC | \(\overline{c}\) | \(\mathrm{[m]}\) |
| 全機揚力傾斜 | \(C_{L}\) | \(\mathrm{[-]}\) |
| 全機揚力傾斜 | \(C_{L_{\alpha}}\) | \(\mathrm{[1/deg]}\) |
| 無次元安定微係数 | \(C_{m_{\alpha}}\) | \(\mathrm{[1/deg]}\) |
| \(C_{m_{\dot{\alpha}}}\) | \(\mathrm{[1/rad]}\) | |
| \(C_{m_{q}}\) | \(\mathrm{[1/rad]}\) | |
| 重力加速度 | \(g\) | \(\mathrm{[m/s^2]}\) |
| 重心位置 | \(h\) | \(\mathrm{[-]}\) |
| 主翼空力中心位置 | \(h_{n_{w}}\) | \(\mathrm{[-]}\) |
| 慣性モーメント(ピッチ方向) | \(I_{yy}\) | \(\mathrm{[kg\:m^2]}\) |
| 重心-水平尾翼空力中心間距離 | \(l_{t}\) | \(\mathrm{[m]}\) |
| 全備重量 | \(M\) | \(\mathrm{[kg]}\) |
| 有次元安定微係数 | \(M'_{q}\),\(M_{q}\),\(M_{\dot{\alpha}}\) | \(\mathrm{[1/s]}\) |
| \(M'_{\alpha}\),\(M_{\alpha}\) | \(\mathrm{[1/s^2]}\) | |
| 加重倍数 | \(n\) | \(\mathrm{[G]}\) |
| 主翼面積 | \(S\) | \(\mathrm{[m^2]}\) |
| 対気速度 | \(V\) | \(\mathrm{[m/s]}\) |
| 水平尾翼容積比 | \(V_{H}\) | \(\mathrm{[-]}\) |
| 迎角 | \(\alpha\) | \(\mathrm{[deg]}\) |
| つり合い迎角 | \(\alpha_{0}\) | \(\mathrm{[deg]}\) |
| エレベータ舵角 | \(\delta e\) | \(\mathrm{[deg]}\) |
| 吹き下ろし角 | \(\varepsilon\) | \(\mathrm{[deg]}\) |
| ピッチ角 | \(\theta\) | \(\mathrm{[deg]}\) |
| 空気密度 | \(\rho\) | \(\mathrm{[kg/m^3]}\) |
| 固有振動数 | \(\omega_{n_{_{SP}}}\) | \(\mathrm{[rad/s]}\) |
加速度感\(n/\alpha\)
加速度感(normal acceleration sensitivity, \(n/\alpha\)と表記)とは,単位迎角当たりの加重倍数の増加量の定常値である.(中略)パイロットが飛行経路を変化させたい場合は,昇降舵を操作して迎角を変え,これによって生ずる揚力増分により垂直加速度を発生させる.したがって単位迎角当たりの加重倍数(揚力を機体重量で割った値)の増加量を表す加速度感\(n/\alpha\)は,縦の操縦性を支配する最も基本的なパラメータといえる.
加速度感\(n/\alpha\)は,他のパラメータとともに設計基準の中で使用される.
青本 p.66
加速度感\(n/\alpha\)は次のように計算する
\begin{equation}
\frac{n}{\alpha}
=\frac{\rho V^{2} S C_{L_{\alpha}}}{2Mg}\frac{180}{\pi} \:\mathrm{[G/rad]}
\tag{青本 2.6-26}
\end{equation}
固有振動数\(\omega_{n_{_{SP}}}\)
縦の短周期運動の非減衰固有振動数\(\omega_{n_{_{SP}}} \) は次のように計算する
\begin{equation}
\omega_{n_{_{SP}}}=\sqrt{M'_{q}\overline{Z}_{\alpha}-M'_{\alpha}} \quad \mathrm{[rad/s]}
\tag{青本 2.3-10}
\end{equation}
有次元安定微係数は次のように計算できる
\begin{align}
&\begin{array}{rl}
\overline{Z}_{\alpha}
&=-\frac{\rho V S}{2M}\left(C_{L_{\alpha}}+2C_{L}\tan{\alpha_{0}}\frac{\pi}{180}\right)\frac{180}{\pi}
\end{array}\tag{青本 2.2-37} \\ \\
&\begin{array}{rl}
M_{\alpha}
&=\frac{\rho V^2 S \overline{c}}{2I_{yy}}C_{m_{\alpha}}\frac{180}{\pi}
\\ \\
M_{q}
&=\frac{\rho V S \overline{c}^2}{4I_{yy}}C_{m_{q}}
\\ \\
M_{\dot{\alpha}}
&=\frac{\rho V S \overline{c}^2}{4I_{yy}}C_{m_{\dot{\alpha}}}
\end{array}\tag{青本 2.2-38} \\ \\
&\begin{array}{rl}
M'_{q}&=M_{q}+M_{\dot{\alpha}} \\ \\
M'_{\alpha}&=M_{\alpha}+M_{\dot{\alpha}}\overline{Z}_{\alpha}
\end{array}\tag{青本 2.2-39} \\ \\
\end{align}
無次元安定微係数は次のように計算できる
\begin{align}
&C_{m_{\alpha}}=-a_{w}\left\{h_{n_{w}}+\frac{a_{t}}{a_{w}}\left(1-\frac{\partial \varepsilon}{\partial \alpha}\right)V_{H}-h\right\}
\tag{白本 4.40} \\ \\
&C_{m_{q}}=-2V_{H}\frac{l_{t}}{\overline{c}}a_{t}\frac{180}{\pi}
\tag{白本 4.48} \\ \\
&C_{m_{\dot{\alpha}}}=-2V_{H}\frac{l_{t}}{\overline{c}}\frac{\partial \varepsilon}{\partial \alpha}a_{t}\frac{180}{\pi}
\tag{白本 4.51} \\ \\
&V_{H}=\frac{S_{t}l_{t}}{S\overline{c}}
\tag{白本 4.37} \\ \\
\end{align}
CAP
CAP(Control Anticipation Parameter)は,パイロットが経路角制御を行う場合,初期のピッチ角速度応答を予測して操縦しているという仮定から考えられたパラメータである.
青本 p.69
CAPは,パイロットのエレベータの初期操舵\(\delta e\)に対するピッチ角加速度\(\ddot{\theta}\)と最終的なエレベータ操舵\(\delta e\)に対する加重倍数応答\(\Delta n_{z}\)の比によって次のように与えられる
\begin{equation}
{CAP}=\frac{\left.(\ddot{\theta}/\delta e)\right|_{t=0}}{\left.(\Delta n_{z}/\delta e)\right|_{t=\infty}}\frac{\pi}{180}
\end{equation}
CAPは \(\omega_{n_{_{SP}}}\)と \(n/\alpha\) を使って次のように近似できる
\begin{equation}
{CAP}=\frac{\omega_{n_{_{SP}}}^{2}}{n/\alpha}
\end{equation}
CAPはパイロットが操縦の際に感じるであろうピッチ角加速度と垂直加速度の比として与えられており,大きすぎても小さすぎても機体の運動とパイロットの感覚にずれが生じてしまう
MIL-F-8785Cでは,CAPが実質的に\(\omega_{n_{_{SP}}}\)の値を制限している
QX-20における値
それでは実際に,QX-20を題材に機体性能をプロットしてみる
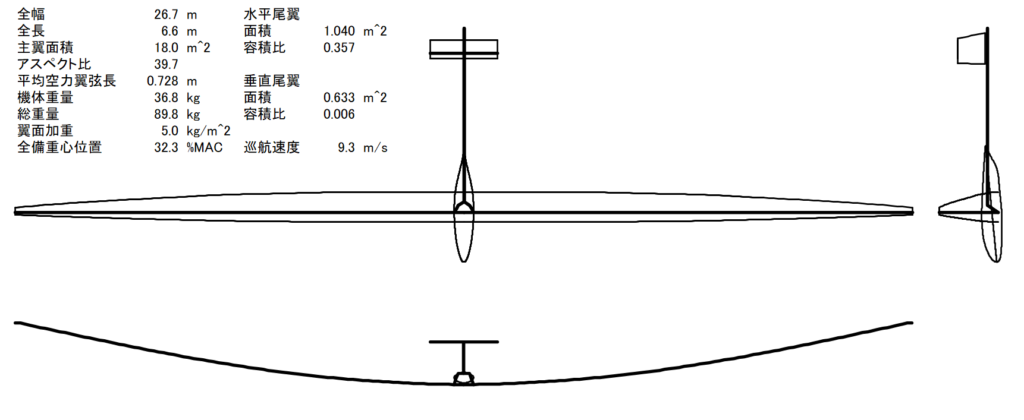
QX-20は以下に示すような機体である
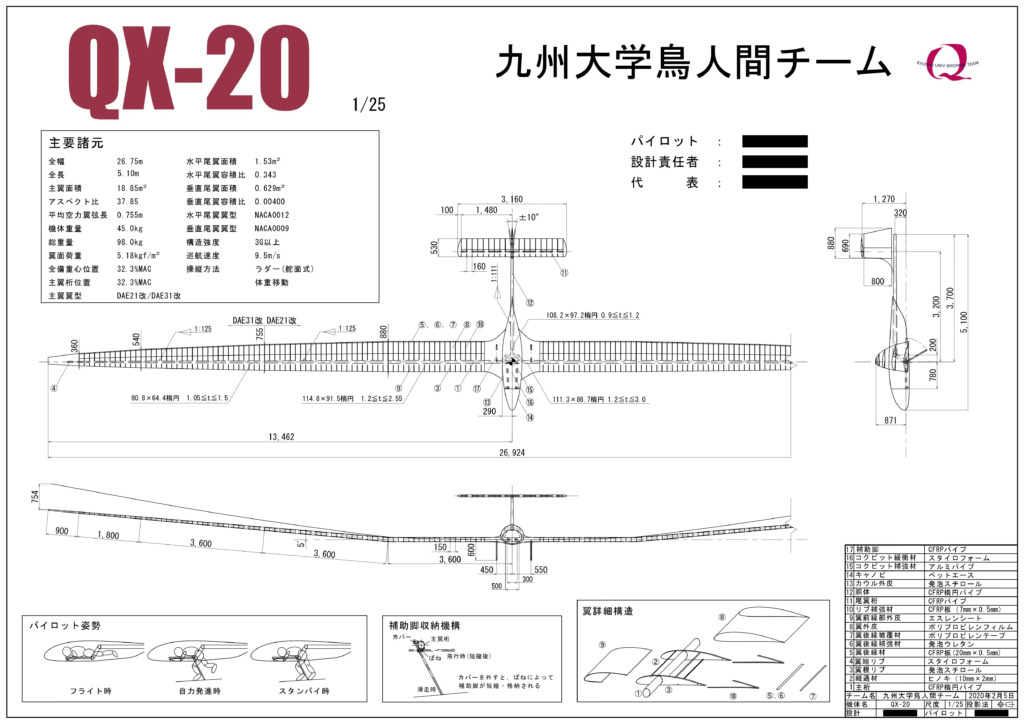
QX-20で \(n/\alpha\),\(\omega_{n_{_{SP}}}\),\({CAP}\)を計算すると次のようになる
\begin{align}
&\frac{n}{\alpha} =\frac{1.164\times9.600^{2}\times18.817\times0.115}{2\times98.613\times9.795}\frac{180}{\pi} =6.904 \quad\mathrm{[G/rad]} \\ \\ &\omega_{n_{_{SP}}}=\sqrt{(-7.578)\times(-7.070)-(-16.749)} =8.386 \quad\mathrm{[rad/s]} \\ \\
&{CAP}=\frac{8.386^{2}}{6.904}=10.186
\end{align}
この値をFigure2にプロットすると次のようになる
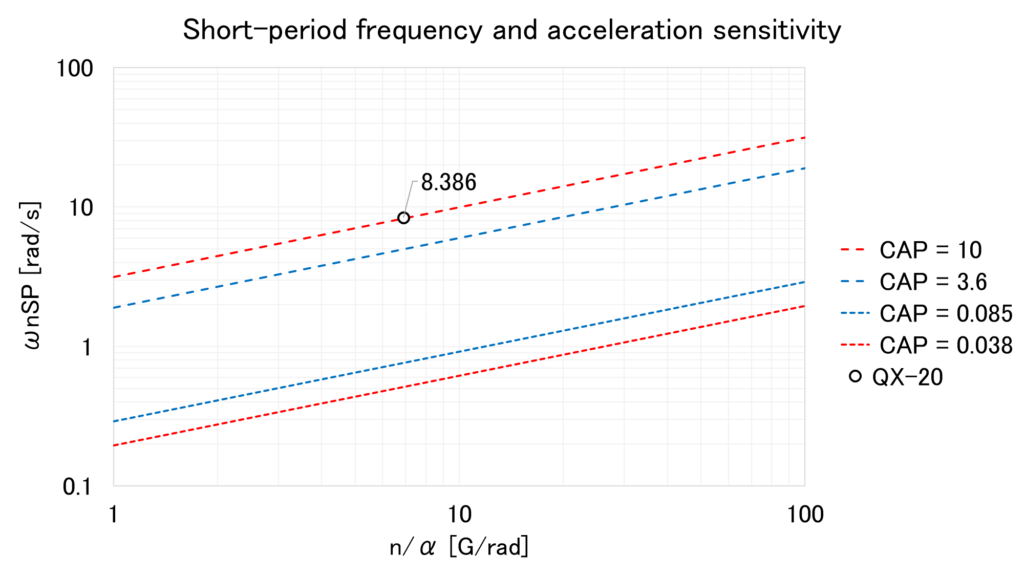
グラフを読み取ると,QX-20はぎりっぎりで「レベル2:適切だが,任務達成に作業負担が増大し任務の効果が低下」に入っていることがわかる
鳥コン滑空機の任務を「琵琶湖の風の状況と自機の状況を的確に把握し,常に最適滑空角を維持してフライトし続ける」だとすれば,QX-20は飛行特性が微妙で,上記任務を達成するにはパイロットに負担を強いるか,任務の効果が下がって最大飛距離が出せないか,もしくはその両方が起こりうるということである
ちょっとした考察
おそらく米軍のパイロットに対するヒアリングから作成されたであろうMIL-F-8785Cをハンググライダー勢が多くを占める鳥コン滑空機に適用する意味はあまりないかもしれないが,もし今後グライダーなどで練習を積んだパイロットがグライダーのインターフェースで鳥コン滑空機を操縦することがあれば,鳥コン滑空機の飛行性に対して何かしらの違和感を覚えるかもしれない
そんなときのために,CAPが何をパラメーターとして変化しているのか考えてみる
CAPの式にいろいろな値の定義式をぶち込んでいく
\begin{align}
{CAP}
&=\frac{\omega_{n_{_{SP}}}^{2}}{n/\alpha}
=\frac{M'_{q}\overline{Z}_{\alpha}-M'_{\alpha}}{n/\alpha}
=\frac{(M_{q}+M_{\dot{\alpha}})\overline{Z}_{\alpha}-(M_{\alpha}+M_{\dot{\alpha}}\overline{Z}_{\alpha})}{n/\alpha}
=\frac{M_{q}\overline{Z}_{\alpha}-M_{\alpha}}{n/\alpha} \\ \\
&=\frac{\left(\frac{\rho V S \overline{c}^2}{4I_{yy}}C_{m_{q}}\right)\left(-\frac{\rho V S}{2M}\left(C_{L_{\alpha}}+2C_{L}\tan{\alpha_{0}}\frac{\pi}{180}\right)\frac{180}{\pi}\right)-\left(\frac{\rho V^2 S \overline{c}}{2I_{yy}}C_{m_{\alpha}}\frac{180}{\pi}\right)}{\frac{\rho V^{2} S C_{L_{\alpha}}}{2Mg}\frac{180}{\pi}} \\ \\
&=\frac{
-\frac{\rho^2 V^2 S^2 \overline{c}^2}{8I_{yy}M}\left(-2V_{H}\frac{l_{t}}{\overline{c}}a_{t}\frac{180}{\pi}\right)
C'_{L_{\alpha}}
-\frac{\rho V^2 S \overline{c}}{2I_{yy}}\left[-a_{w}\left\{h_{n_{w}}+\frac{a_{t}}{a_{w}}\left(1-\frac{\partial \varepsilon}{\partial \alpha}\right)V_{H}-h\right\}
\right]
\frac{180}{\pi}
}{\frac{\rho V^{2} S C_{L_{\alpha}}}{2Mg}\frac{180}{\pi}} \\ \\
&=\cdots \\ \\
&=\frac{Mg}{I_{yy}}\frac{a_{w}}{C_{L_{\alpha}}}\overline{c}\left\{h_{n_{w}}+\frac{a_{t}}{a_{w}}\left(1-\frac{\partial \varepsilon}{\partial \alpha}+\frac{\rho S l_{t}}{2M}C'_{L_{\alpha}}\right)V_{H}-h\right\}\frac{180}{\pi}
\end{align}
上記の式変形で,\(CAP\)は全備重量\(M\)に比例し,ピッチ方向の慣性モーメント\(I_{yy}\)に反比例することが分かった(ほかのパラメータは恣意的にいじりにくい)
つまり,\(CAP\)を適正範囲に近づけるためには,「慣性モーメント\(I_{yy}\)がそこそこ大きく,全備重量\(M\)が小さい軽量な機体」を設計する必要がある
実際,QX-20の初期上反をなくして軽量化し,エレベータ操舵ができるよう胴体長さを長くすると\(CAP\)はそれなりに改善される
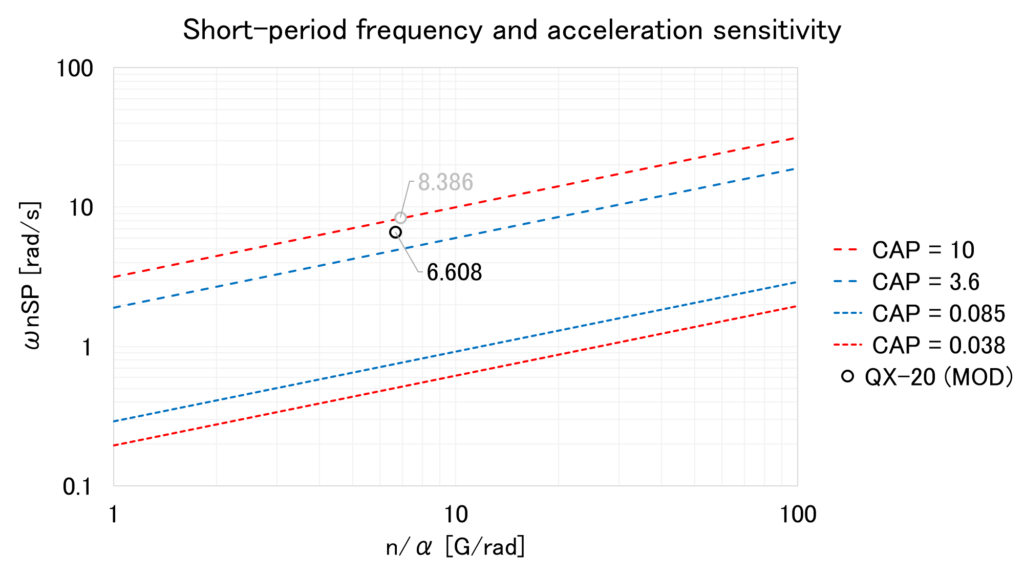
まとめ
MIL-F-8785Cを考慮して鳥コン滑空機を設計してみると,近年の鳥コン滑空機の主流である「高翼面荷重の高速機でハングのように操縦できる慣性モーメントの小さい機体」と逆行する設計思想になった
もしかしたら某大会の出場書類で,「MIL規格に準拠した設計」というワードがみられる日が来るかもしれない
↓関連記事

コメント