scipy.interpolate.BSplineで次数上げを実装する

scipy.interpolate.BSplineにデフォルトで実装されていない次数上げ（degree elevation）の機能を補った自作クラスMyBSplineの作る

はじめに
理論
実装
プログラムの解説
おわりに

はじめに

scipy.interpolate.BSplineはBSpline曲線を作成するためのPythonライブラリである

この記事では、scipy.interpolate.BSplineにデフォルトで実装されていない次数上げ（degree elevation）の機能を補った自作クラスMyBSplineの作り方について説明する

↓公式ドキュメント

BSpline — SciPy v1.16.1 Manual

↓関連記事

↓参考文献

リンク

なお、この記事の数式に付されている式番号は、この参考文献の式番号と対応するようにしている

それではいってみよう

理論

Bezier曲線（制御点数\(n=k+1\)のBSpline曲線）の階数上げは解析的に計算することができる

\(k\)階のBezier曲線を\(k+1\)階に階数上げするとき、階数上げをした後のBezier曲線の制御点\(\mathbf{q}_i\)は次の式で計算できる

\begin{align}
\mathbf{q}_{i} &= \alpha_i \, \mathbf{p}_{i-1} + (1-\alpha_i) \, \mathbf{p}_i \\\\
\alpha_i &= \frac{i}{n}, \qquad i = 0,~ \cdots,~ n
\tag{5.6.1}
\end{align}

このとき、もともとの制御点\(\mathbf{p}_{i}\)が\(i=0,~ \cdots,~ n-1\)の\(n\)個だったのに対し、階数上げ後の新しい制御点\(\mathbf{q}_i\)は階数が1つ増えたことにより、\(i=0,~ \cdots,~ n\)の\(n+1\)個になっている

例えば、\(k=4\)、\(n=k+1=5\)のときは次のようになる

\begin{alignat}{4}
\mathbf{q}_0 &= \mathbf{p}_0 & & & & \\\\
\mathbf{q}_1 &= \frac{1}{5}\, &\mathbf{p}_0 &+& \frac{4}{5}\, &\mathbf{p}_1 \\\\
\mathbf{q}_2 &= \frac{2}{5}\, &\mathbf{p}_1 &+& \frac{3}{5}\, &\mathbf{p}_2 \\\\
\mathbf{q}_3 &= \frac{3}{5}\, &\mathbf{p}_2 &+& \frac{2}{5}\, &\mathbf{p}_3 \\\\
\mathbf{q}_4 &= \frac{4}{5}\, &\mathbf{p}_3 &+& \frac{1}{5}\, &\mathbf{p}_4 \\\\
\mathbf{q}_5 &= \mathbf{p}_4 & & & & \\\\
\end{alignat}

Bezier曲線の階数上げを利用すれば、以下の手順で\(k\)階のBSpline曲線の階数を\(k+1\)階に階数上げることができる

BSpline曲線の各ノットの多重度が\(k\)になるまでノットを挿入し、すべてのセグメントをBezier曲線にする（\(\mathbf{t} ~ \rightarrow \, \mathbf{t}'\)）
各セグメントに対応する制御点\(\mathbf{p}_i\)のまとまりを抽出する
各セグメントごとにBezier曲線の階数上げの手法を適用し、新しい制御点\(\mathbf{q}_i\)を計算する
ノットベクトル\(\mathbf{t}'\)のすべての多重ノット（多重端末ノット含む）の多重度を1つ増やす（\(\mathbf{t}' \, \rightarrow \, \mathbf{\hat{t}}\)）
ノットベクトル\(\mathbf{\hat{t}}\)、階数\(k+1\)、制御点\(\mathbf{q}_i\)から新しいBSpline曲線を定義する

実装

コード全文はこれ

MyBSpline

import numpy as np
from scipy.interpolate import BSpline

class MyBSpline(BSpline):

    def __init__(self, t=None, c=None, k=4):
        
        # BSpline の初期化
        if t is not None and c is not None:
            super().__init__(t, c, k)


    def _bspline_to_bezier(self):
        """
        bspline の内部ノットそれぞれについてmultiplicity が k 未満なら不足分を挿入して各セグメントをbezier曲線にする。

        Parameters
        ----------
        self : scipy.interpolate.BSpline
            入力スプライン（変更せず新しい BSpline を返す）
        
        Returns
        -------
        scipy.interpolate.BSpline
            必要なノット挿入を行った新しい BSpline オブジェクト
        """

        # 目標 multiplicity を決定
        t = np.asarray(self.t)
        k = self.k

        # 内部ノットとその多重度を取得
        unique, counts = np.unique(t, return_counts=True)
        if unique.size <= 2:
            return self  # 内部ノットがない -> そのまま返す
        t_internal = unique[1:-1]
        mult_internal = counts[1:-1]

        # どの内部ノットをどれだけ追加するかを決める（必要なら挿入）
        bezier = self
        for u, mult in zip(t_internal, mult_internal):
            if int(mult) < k:
                need = int(k - int(mult))
                # insert_knot は指定回数を一度に挿入できる (戻り値は新しい BSpline)。
                bezier = bezier.insert_knot(float(u), m=need)
        return bezier

    def _elevate_bezier_segments(self, c, r):
        """
        Bézier制御点列の次数をr段階昇格する。

        Parameters
        ----------
        c : ndarray of shape (n_points, dim)
            元の制御点列
        r : int
            昇格段数（0ならそのまま返す）

        Returns
        -------
        ndarray of shape (n_points + r, dim)
            次数上げ後の制御点列
        """
        q = np.asarray(c, dtype=float)
        if q.ndim == 1:
            q = q[:, None]  # (n_points, 1)

        for _ in range(r):
            n = len(q) - 1  # 現在の次数
            alpha = np.arange(1, n + 1) / (n + 1)  # ベクトル化された係数
            # q0 と qn+1 を固定し、中間は線形結合
            q = np.vstack((
                q[0],
                (alpha[:, None] * q[:-1] + (1 - alpha)[:, None] * q[1:]),
                q[-1]
            ))
        return q

    def _extract_bezier_segments(self):
        """
        与えられたBスプラインをBézier区間に分割して制御点列を返す。

        Parameters
        ----------
        self : scipy.interpolate.BSpline

        Returns
        -------
        list of ndarray
            各Bézier区間の制御点列
        """

        t = np.asarray(self.t)
        c = np.asarray(self.c)
        if c.ndim == 1:
            c = c[:, None]

        k = self.k
        t_unique = np.unique(t)
        n_seg = max(1, t_unique.size - 1)

        c_seg = [
            c[i * k : i * k + k + 1]
            for i in range(n_seg)
        ]
        return c_seg

    def degree_elevation(self, k_target):
        """
        BスプラインをBézier区間ごとに次数上げし、再結合して新しいBスプラインを返す。

        Parameters
        ----------
        self : scipy.interpolate.BSpline
        k_target : int
            目標の次数（現在の次数以上）

        Returns
        -------
        scipy.interpolate.BSpline
            次数上げ後の新しいBスプライン
        """
        k = self.k
        if k_target <= k:
            return self  # 昇格不要
        
        # 1) ノット挿入でbsplineをbezierに変換
        bezier = self._bspline_to_bezier()

        # 2) 制御点をBézier区間に分割
        c_seg = self._extract_bezier_segments()

        # 3) 各Bézier区間を次数上げ
        r = k_target - k
        c_seg_new = [self._elevate_bezier_segments(seg, r) for seg in c_seg]

        # 4) 全制御点列を再結合
        dim = c_seg_new[0].shape[1]
        n_seg = len(c_seg_new)
        n_new = n_seg * k_target + 1
        c_new = np.zeros((n_new, dim), dtype=float)
        for i, q in enumerate(c_seg_new):
            c_new[i * k_target : i * k_target + k_target + 1, :] = q

        # 5) ノットベクトルの多重度をk_targetに更新
        t_new = [self.t[0]] + np.repeat(np.unique(self.t), k_target).tolist() + [self.t[-1]]
        
        # 6) 新しいBスプラインを作成
        return BSpline(t_new, c_new.squeeze(), k_target)

使用例

以下のBSpline曲線を例として説明する

\begin{align}
k &= 2 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0.25,~ 0.5,~ 0.75,~ 1,~ 1,~ 1] \\
m &= 9 \\
n &= m - (k + 1) = 9 - 3 = 6 \\
\end{align}

import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
np.set_printoptions(formatter={'float':'{:3.2f}'.format}, linewidth=999)

# ===== set parameter (t, c, k) =====
k = 2
c = np.array([[0, 0], [1, 2], [2, 2], [3, 0], [4, -1],[5, 0]])
n = len(c)
m = n + (k + 1)
t = [0] * k + np.linspace(0, 1, m - 2 * k).tolist() + [1] * k

# ===== get original bspline =====
bspline0 = BSpline(t, c, k)

print('\noriginal:\n')
print('  t:', bspline0.t)
print('  c.shape:', bspline0.c.shape)
print('  k:', bspline0.k)
plot([bspline0])

original:

  t: [0.00 0.00 0.00 0.25 0.50 0.75 1.00 1.00 1.00]
  c.shape: (6, 2)
  k: 2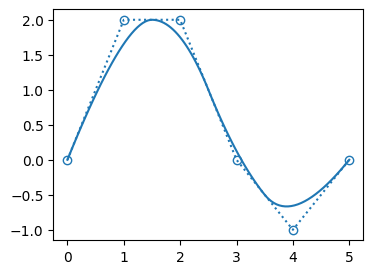

# ===== degree elevation ===== 
k_target = 4
bspline = MyBSpline(t, c, k)
bspline = bspline.degree_elevation(k_target)

print('\ndegree elevation:\n')
print('  t:', bspline.t)
print('  c.shape:', bspline.c.shape)
print('  k:', bspline.k)
plot([bspline0, bspline])

degree elevation:

  t: [0.0 0.0 0.0 0.0 0.0 0.2 0.2 0.2 0.2 0.4 0.4 0.4 0.4 0.6 0.6 0.6 0.6 0.8 0.8 0.8 0.8 1.0 1.0 1.0 1.0 1.0]
  c.shape: (21, 2)
  k: 4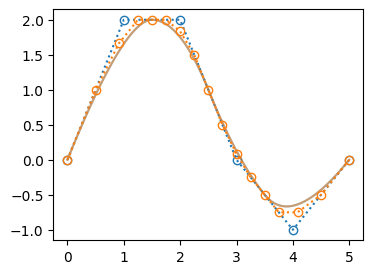

もともと\(k=2\)だったBSpline曲線が、その形状を維持したまま、\(k=4\)まで次数上げされていることがわかる

プログラムの解説

ここからはMyBSplineクラスの各メソッドについて説明する

自作クラスの定義

scipy.interpolate.BSplineでは次数上げの機能が実装されていないので、BSplineクラスを継承した自作クラスMyBSplineクラスを作り、次数上げの機能を実装する

from scipy.interpolate import BSpline

class MyBSpline(BSpline):

    def __init__(self, t=None, c=None, k=4):
        
        # BSpline の初期化
        if t is not None and c is not None:
            super().__init__(t, c, k)

    # ここから自作メソッドを定義

MyBSplineクラスはBSplineクラスを継承しているので、BSplineクラスが持つメソッドはそのまま使うことができる

MyBSpline.degree_elevation(self, k_target)

BスプラインをBézier区間ごとに次数上げし、再結合して新しいBスプラインを返すメソッド

degree_elevation(self, k_target)

def degree_elevation(self, k_target):
    """
    BスプラインをBézier区間ごとに次数上げし、再結合して新しいBスプラインを返す。

    Parameters
    ----------
    k_target : int
        目標の次数（現在の次数以上）

    Returns
    -------
    scipy.interpolate.BSpline
        次数上げ後の新しいBスプライン
    """

    k = self.k
    if k_target <= k:
        return self  # 次数上げ不要
    
    # 1) ノット挿入でbsplineをBézierに変換
    bezier = self._bspline_to_bezier()

    # 2) 制御点をBézier区間に分割
    c_seg = self._extract_bezier_segments()

    # 3) 各Bézier区間を次数上げ
    r = k_target - k
    c_seg_new = [self._elevate_bezier_segments(seg, r) for seg in c_seg]

    # 4) 全制御点列を再結合
    dim = c_seg_new[0].shape[1]
    n_seg = len(c_seg_new)
    n_new = n_seg * k_target + 1
    c_new = np.zeros((n_new, dim), dtype=float)
    for i, q in enumerate(c_seg_new):
        c_new[i * k_target : i * k_target + k_target + 1, :] = q

    # 5) ノットベクトルの多重度をk_targetに更新
    t_new = [self.t[0]] + np.repeat(np.unique(self.t), k_target).tolist() + [self.t[-1]]
    
    # 6) 新しいBスプラインを作成
    return BSpline(t_new, c_new.squeeze(), k_target)

引数

k_target : int
目標の次数（現在の次数以上）

戻り値

scipy.interpolate.BSpline
次数上げ後の新しいBスプライン

理論の章で説明した手順通りに次数上げを行っている

階数上げ前後を比較するとこんな感じになる

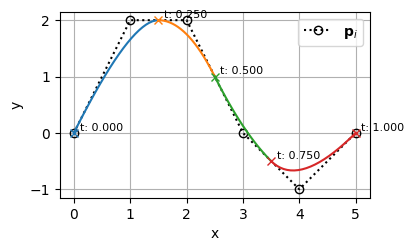
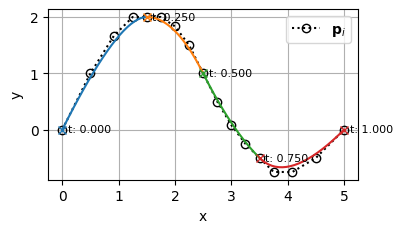
階数が増えたことで、制御点も増え、BSpline曲線の表現力が上がっていることがわかる

MyBSpline._bspline_to_bezier(self)

bsplineの内部ノットそれぞれについて多重度（multiplicity）が\(k\)未満のノットに不足分を挿入し、各セグメントをbezier曲線にする内部メソッド

_bspline_to_bezier(self)

def _bspline_to_bezier(self):
    """
    bspline の内部ノットそれぞれについてmultiplicity が k 未満なら不足分を挿入して各セグメントをbezier曲線にする。

    Parameters
    ----------
    self : scipy.interpolate.BSpline
        入力スプライン（変更せず新しい BSpline を返す）
    
    Returns
    -------
    scipy.interpolate.BSpline
        必要なノット挿入を行った新しい BSpline オブジェクト
    """

    # 目標 multiplicity = kを決定
    t = np.asarray(self.t)
    k = self.k

    # 内部ノットとその多重度を取得
    unique, counts = np.unique(t, return_counts=True)
    if unique.size <= 2:
        return self  # 内部ノットがない -> そのまま返す
    t_internal = unique[1:-1]
    mult_internal = counts[1:-1]

    # どの内部ノットをどれだけ追加するかを決める（必要なら挿入）
    bezier = self
    for u, mult in zip(t_internal, mult_internal):
        if int(mult) < k:
            need = int(k - int(mult))
            # insert_knot は指定回数を一度に挿入できる (戻り値は新しい BSpline)。
            bezier = bezier.insert_knot(float(u), m=need)

    return bezier

引数

なし

戻り値

scipy.interpolate.BSpline
必要なノット挿入を行った新しい BSpline オブジェクト

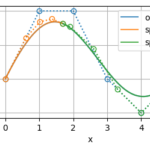
このメソッドを実行した時点でのbsplineは以下のようになっている

bezier:

  t: [0.00 0.00 0.00 0.25 0.25 0.50 0.50 0.75 0.75 1.00 1.00 1.00]
  c.shape: (9, 2)
  k: 2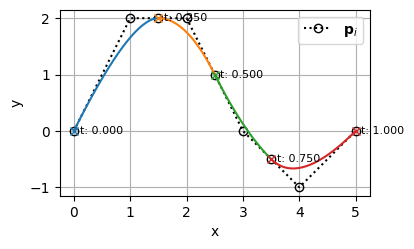

ノット挿入によって、BSpline曲線の形状を維持したまま内部ノットの多重度が\(k\)になり、それぞれのセグメントがBezier曲線になっていることがわかる

MyBSpline._extract_bezier_segments(self)

与えられたBスプラインをBézier区間に分割して制御点列を返す内部メソッド

_extract_bezier_segments(self)

def _extract_bezier_segments(self):
    """
    与えられたBスプラインをBézier区間に分割して制御点列を返す。

    Parameters
    ----------
    self : scipy.interpolate.BSpline

    Returns
    -------
    list of ndarray
        各Bézier区間の制御点列
    """

    t = np.asarray(self.t)
    c = np.asarray(self.c)
    if c.ndim == 1:
        c = c[:, None]

    k = self.k
    t_unique = np.unique(t)
    n_seg = max(1, t_unique.size - 1)

    c_seg = [
        c[i * k : i * k + k + 1]
        for i in range(n_seg)
    ]

    return c_seg

引数

なし

戻り値

list of ndarray
各Bézier区間の制御点群のリスト

Bezier曲線の制御点数は\(n=k+1\)なので、終点と始点を被らせつつ\(k+1\)個ずつ制御点を区切っていく

今回の例でいうと、ノットを挿入して9個になった制御点を\(k+1=3\)個ずつ、4つのセグメントで区切る

\begin{align}
\mathbf{P} = & [\mathbf{p}_0,~ \mathbf{p}_1,~ \cdots,~ \mathbf{p}_8] \\\\
& \begin{cases}
[\mathbf{p}_0,~ \mathbf{p}_1,~ \mathbf{p}_2], \qquad & u=0 \sim 0.25 \\
[\mathbf{p}_2,~ \mathbf{p}_3,~ \mathbf{p}_4], \qquad & u=0.25 \sim 0.5 \\
[\mathbf{p}_4,~ \mathbf{p}_5,~ \mathbf{p}_6], \qquad & u=0.5 \sim 0.75 \\
[\mathbf{p}_6,~ \mathbf{p}_7,~ \mathbf{p}_8], \qquad & u=0.75 \sim 1 \\
\end{cases}
\end{align}

MyBSpline._elevate_bezier_segments(self, c, r)

Bézier制御点列の次数をr階だけ階数上げする内部メソッド

_elevate_bezier_segments(self, c, r)

def _elevate_bezier_segments(self, c, r):
    """
    Bézier制御点列の次数をr階階数上げする。

    Parameters
    ----------
    c : ndarray of shape (n_points, dim)
        元の制御点列
    r : int
        階数上げ段数（0ならそのまま返す）

    Returns
    -------
    ndarray of shape (n_points + r, dim)
        次数上げ後の制御点列
    """
    q = np.asarray(c, dtype=float)
    if q.ndim == 1:
        q = q[:, None]  # (n_points, 1)

    for _ in range(r):
        n = len(q) - 1  # 現在の次数
        alpha = np.arange(1, n + 1) / (n + 1)  # ベクトル化された係数
        # q0 と qn+1 を固定し、中間は線形結合
        q = np.vstack((
            q[0],
            (alpha[:, None] * q[:-1] + (1 - alpha)[:, None] * q[1:]),
            q[-1]
        ))

    return q

引数

c : ndarray of shape (n_points, dim)
元の制御点列
r : int
階数上げ数（0ならそのまま返す）

戻り値

ndarray
次数上げ後の制御点列

ちょっとわかりにくいが、この式を計算している

\begin{align}
\mathbf{q}_{i} &= \alpha_i \, \mathbf{p}_{i-1} + (1-\alpha_i) \, \mathbf{p}_i \\\\
\alpha_i &= \frac{i}{n}, \qquad i = 0,~ \cdots,~ n
\end{align}

今回の例は\(k=2\)から\(k=4\)まで階数上げを行うので、上記の式を2回繰り返す必要がある

おわりに

scipy.interpolate.BSplineにデフォルトで実装されていない次数上げ（degree elevation）の機能を補った自作クラスMyBSplineの作った

この教科書的なアルゴリズムだと制御点が増えると計算量がだいぶしんどくなるので、より効率的なアルゴリズムがたくさんようである

↓関連記事