BSpline曲線について、知っておくと便利な基本的な操作について説明する
はじめに
BSpline曲線とは、言わずと知れた「滑らかな曲線」を作る技術である
工学の世界では主にCADなどに用いられ、世界中のエンジニアの手元で日夜あらゆる滑らかな曲線を生成している
この記事では、BSpline曲線の操作について数値例や定式化も含めて解説する
この記事で使うような技術を使ってBSpline曲線そのものをこねくり回す機会はあまりないかもしれないが、CADで滑らかな曲線を自在に描けるようになりたい人たちの一助になれば幸いである
↓関連記事
↓参考文献
なお、この記事の数式に付されている式番号は、この参考文献の式番号と対応するようにしている
BSpline曲線は、その形状を維持したまま
- ノットベクトルを振りなおせる
- ノットを挿入できる
- ノットの多重度を上げられる
- 階数(次数)を上げられる
そして、これらの操作を組み合わせることで
- BSpline曲線を2つに分割できる
- 2つのBSpline曲線を結合できる
- 2つのBSpline曲線の中間曲線を作ることができる
それではいってみよう
ノットベクトルの振り直し
ノットベクトルを\(\mathbf{t}=[0,~ \cdots,~ 1]\)で定義しておくとBSpline曲線のパラメータは\(0 \leq u \leq 1\)となり分かりやすいが、一度定義してしまったBSpline曲線のノットベクトルは後から振りなおすこともできる
ノットベクトルを振りなおすときは、以下の条件を満たすようにする
- 元のノットベクトルとノットの間隔の比をそろえる
- 元のノットベクトルと多重度をそろえる
例えば、以下のBSpline曲線
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}
のノットベクトルを
\begin{align}
\mathbf{t} &= [1,~ 1,~ 1,~ 1,~ 1,~ 2,~ 3,~ 3,~ 3,~ 3,~ 3] \\
\end{align}
として振りなおすとこのようになる
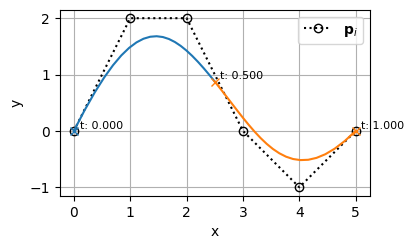
曲線の形は変わらずに、パラメータの値だけが変わっていることが分かる
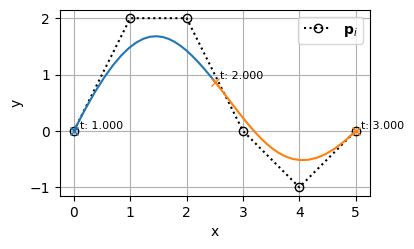
ノットベクトルの間隔の比を変えて
\begin{align}
\mathbf{t} &= [1,~ 1,~ 1,~ 1,~ 1,~ 1.5,~ 3,~ 3,~ 3,~ 3,~ 3] \\
\end{align}
として振りなおすと、BSpline曲線の形が変わってしまう
- ノット間隔の比と多重度をそろえれば、BSpline曲線の形を変えずにノットベクトルを振りなおすことができる
ノットの挿入
BSpline曲線は、形状を全く変えずに、後から好きな位置にノットを追加することができる。
以下で表されるBSpline曲線
\begin{align}
\mathbf{c}(u) &= \sum_{i=0}^{n} N_{i,k}(u) \mathbf{p}_i \\\\
\mathbf{t} &= [t_0,~ t_1,~ \dots,~ t_{m-1}]
\end{align}
について、\(t=u'\)の位置にノットを追加すると次のようになる
\begin{align}
\mathbf{\hat{t}} = [t_0,~ t_1,~ \dots,~ t_r,~ u',~ t_{r+1},~ \dots,~ t_{m-1}],~
\qquad t_r \le u' < t_{r+1}
\tag{5.1.1}
\end{align}
この新しいノットベクトル\(\mathbf{\hat{t}}\)に対して、元の曲線と全く同じ形になるように制御点を1つ増やして再配置することができる(\(m=n+(k+1)\)より、ノットが1つ増えると制御点も1つ増える)
新しい制御点\(\mathbf{q}_{i}\)は次の式で計算する。
\begin{align}
\alpha_i &= \frac{u' - t_i}{t_{i+k-1} - t_i} \\\\
\mathbf{q}_i &= \begin{cases}
\mathbf{p}_i & \quad & (i = 0,~ \cdots,~ r - k) \\
(1 - \alpha_i) \mathbf{p}_{i-1} + \alpha_i \mathbf{p}_i & \quad & (i = r - k +1,~ \cdots,~ r) \\
\mathbf{p}_{i-1} & \quad & (i= r+1,~ \cdots,~ n-1)
\end{cases}
\tag{5.1.2}
\end{align}
こうして計算した新しい制御点\(\mathbf{q}_i\)と、ノット挿入後のノットベクトル\(\mathbf{\hat{t}}\)から計算し直した新しい基底関数\(\hat{N}_{i,k}(u)\)を使えば、ノット挿入後のBSpline曲線が求められる
\begin{align}
\mathbf{\hat{c}}(u) = \sum_{i=0}^{n+1} \hat{N}_{i,k}(u)\, \mathbf{q}_i
\end{align}
scipy.interpolate.BSplineではinsert_knotメソッドとして実装されており、例えば、以下のBSpline曲線
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}
の\(t=0.3\)の位置にノットを挿入すると次のようになる
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.3,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 12 \\
n &= m - (k + 1) = 12 - 5 = 7 \\
\end{align}
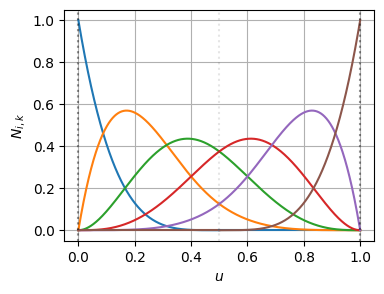
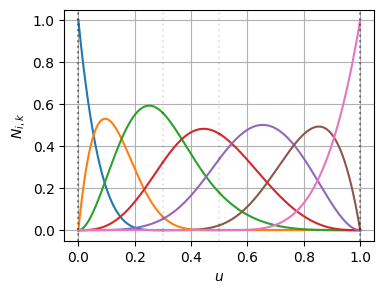
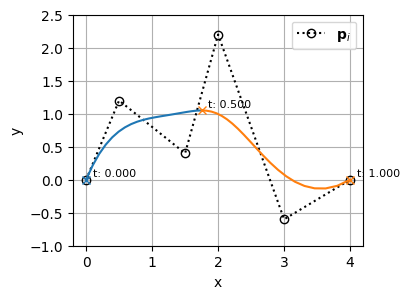
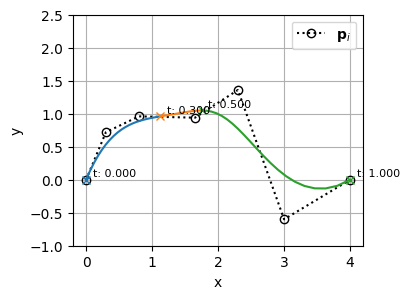
見ての通り、ノットを挿入したことで基底関数の形状は変わっているが、制御点が1つ増え、制御点の位置が再配置されたことにより、BSpline曲線の形状は変わっていない
多重ノット
既存の位置にノットをさらに追加で挿入することによって、曲線を定義した後からでもノットの多重度を上げることもできる
ノットの挿入で後からノットの多重度を上げた場合、BSpline曲線の形状は元の曲線と全く同じに維持されるので、挿入したノットの位置においても元のBSpline曲線の微分の連続性が維持される
例えば、\(t=0.5\)の位置にノットを3つ追加する(\(t=0.5\)のノットの多重度を4にする)と次のようになる
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 14 \\
n &= m - (k + 1) = 14 - 5 = 9 \\
\end{align}
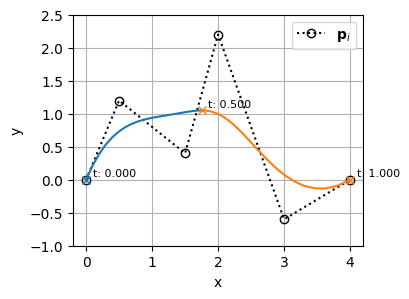
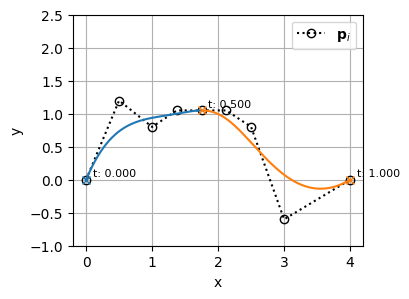
見ての通り、多重度が上がってもBSpline曲線の形状は変わっていない(=微分の連続性も保たれている)ことがわかる
ノットの多重度が上がることで、基底関数の導関数自体は不連続になっている
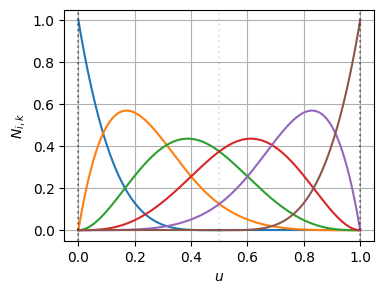
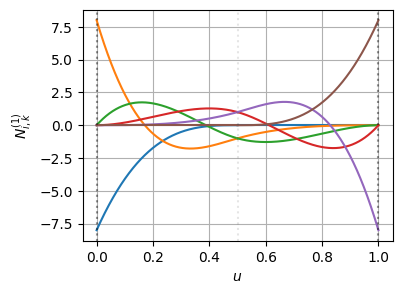
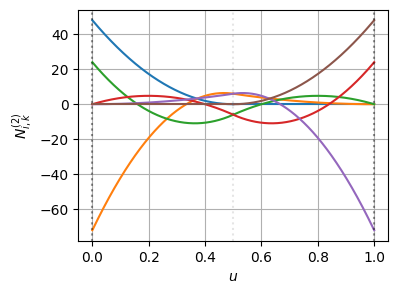
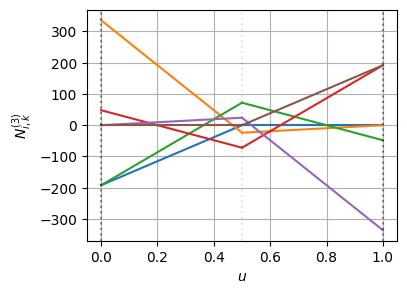
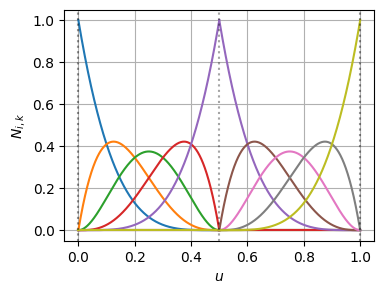
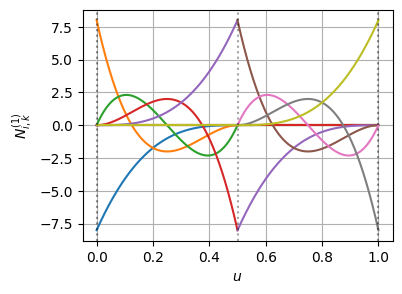
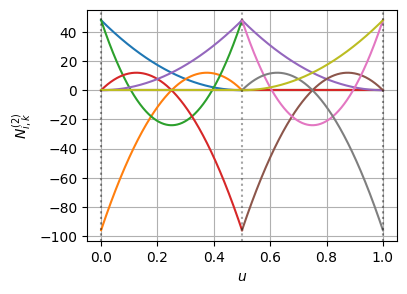
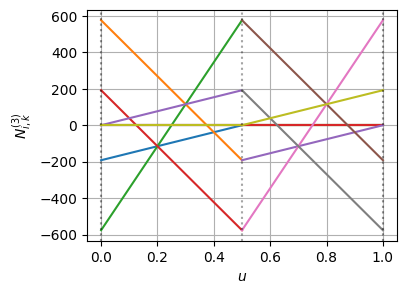
この不連続になった基底関数に対して、BSpline曲線の微分の連続性が保たれるように、制御点が追加・再配置されている
- BSpline曲線は、その形状を維持したまま、任意の位置にノットを挿入できる
- 既存のノット位置にノットを追加で挿入することで、多重ノットにすることもできる
- 後付けで多重ノットにした場合は微分の連続性は下がらない
次数上げ
ノットの挿入と同様に、BSpline曲線の階数についても、曲線の形状を全く変えずに、階数を1増やすことができる
Bezier曲線(制御点数\(n=k+1\)のBSpline曲線)の次数上げは解析的に計算することができる
\(k\)階のBezier曲線を\(k+1\)階に次数上げするとき、次数上げをした後のBezier曲線の制御点\(\mathbf{q}_i\)は次の式で計算できる
\begin{align}
\mathbf{q}_{i} &= \alpha_i \, \mathbf{p}_{i-1} + (1-\alpha_i) \, \mathbf{p}_i, \qquad i = 0,~ \cdots,~ n \\\\
\alpha_i &= \frac{i}{n}
\tag{5.6.1}
\end{align}
このとき、もともとの制御点\(\mathbf{p}_{i}\)が\(i=0,~ \cdots,~ n-1\)の\(n\)個だったのに対し、次数上げ後の新しい制御点\(\mathbf{q}_i\)は階数が1つ増えたことにより、\(i=0,~ \cdots,~ n\)の\(n+1\)個になっている
例えば、\(k=4\)、\(n=k+1=5\)のときは次のようになる
\begin{alignat}{4}
\mathbf{q}_0 &= \mathbf{p}_0 & & & & \\\\
\mathbf{q}_1 &= \frac{1}{5}\, &\mathbf{p}_0 &+& \frac{4}{5}\, &\mathbf{p}_1 \\\\
\mathbf{q}_2 &= \frac{2}{5}\, &\mathbf{p}_1 &+& \frac{3}{5}\, &\mathbf{p}_2 \\\\
\mathbf{q}_3 &= \frac{3}{5}\, &\mathbf{p}_2 &+& \frac{2}{5}\, &\mathbf{p}_3 \\\\
\mathbf{q}_4 &= \frac{4}{5}\, &\mathbf{p}_3 &+& \frac{1}{5}\, &\mathbf{p}_4 \\\\
\mathbf{q}_5 &= \mathbf{p}_4 & & & & \\\\
\end{alignat}
Bezier曲線の次数上げを利用すれば、以下の手順で\(k\)階のBSpline曲線の階数を\(k+1\)階に次数上げることができる
- BSpline曲線の各ノットの多重度が\(k\)になるまでノットを挿入し、すべてのセグメントをBezier曲線にする(\(\mathbf{t} ~ \rightarrow \, \mathbf{t}'\))
- 各セグメントに対応する制御点\(\mathbf{p}_i\)のまとまりごとにBezier曲線の次数上げの手法を適用し、新しい制御点\(\mathbf{q}_i\)を計算する
- ノットベクトル\(\mathbf{t}'\)のすべての多重ノット(多重端末ノット含む)の多重度を1つ増やす(\(\mathbf{t}' \, \rightarrow \, \mathbf{\hat{t}}\))
- ノットベクトル\(\mathbf{\hat{t}}\)、階数\(k+1\)、制御点\(\mathbf{q}_i\)から新しいBSpline曲線を定義する
残念ながらscipy.interpolate.BSplineには次数上げのメソッドは実装されていないので、BSplineクラスを継承した自作クラスであるMyBSplineクラスで次数上げを実装する
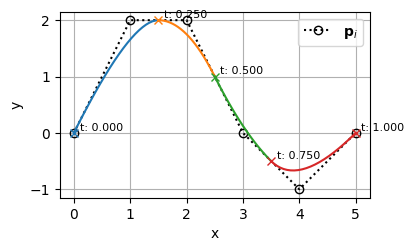
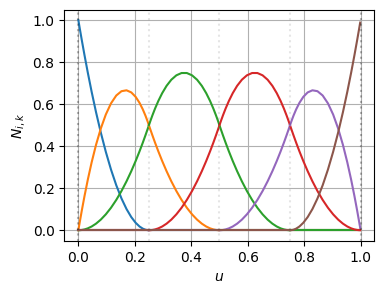
これを使って、以下のBSpline曲線の次数上げを行ってみる
\begin{align}
k &= 2 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0.25,~ 0.5,~ 0.75,~ 1,~ 1,~ 1] \\
m &= 9 \\
n &= m - (k + 1) = 9 - 3 = 6 \\
\end{align}
階数をk=4まで上げると次のようになる
\begin{align}
k &= 4 \\
t &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.25,~ 0.25,~ 0.25,~ 0.25,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.75,~ 0.75,~ 0.75,~ 0.75,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 22 \\
n &= m - (k + 1) = 22 - 5 = 17
\end{align}
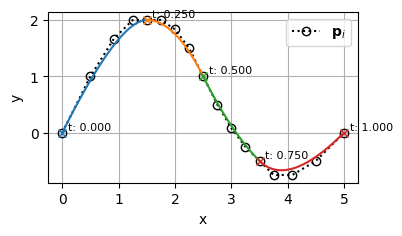
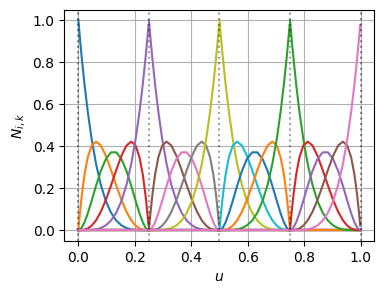
確かに、曲線の形状が保たれたまま、階数が上がっていることが分かる
- BSpline曲線は、その形状を維持したまま、任意の階数まで次数上げができる
BSpline曲線の分割
ここまでに説明した以下の性質:
- ノットは後から任意の位置に挿入可能で、多重ノットにしても元の曲線の形状と微分の連続性は保たれる
- ノットを\(k\)個重ねるとその前後で完全に独立したBSpline曲線に分割される
を組み合わせると、「多重度が\(k\)になるようにノットを挿入すればBSpline曲線を任意の位置で分割することができる」ということが分かる
CADでよくある「曲線の分割」の機能である
手順は以下の通り
- 分割したい位置\(t=u'\)にノットを挿入して多重度を\(k\)にする
- \(t=u'\)を含むようにしてノットベクトルを分割し、ノットベクトルの長さに対応するように制御点も分割する
- 分割したそれぞれのノットベクトルおよび制御点から新しいBSpline曲線を定義する
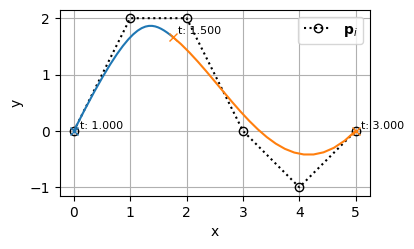
例えば、以下のBSpline曲線:
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}
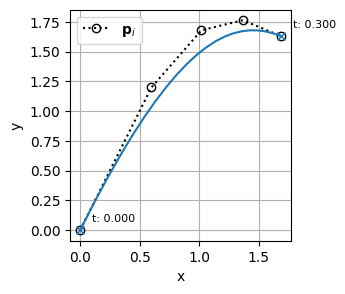
を分割するために、\(t=0.3\)の位置に\(k=4\)個のノットを挿入してみる
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.3,~ 0.3,~ 0.3,~ 0.3,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 15 \\
n &= m - (k + 1) = 15 - 5 = 10 \\
\end{align}
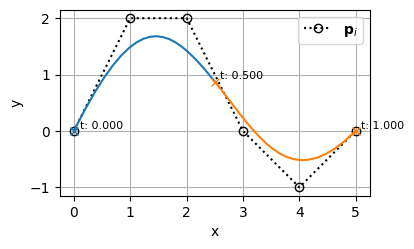
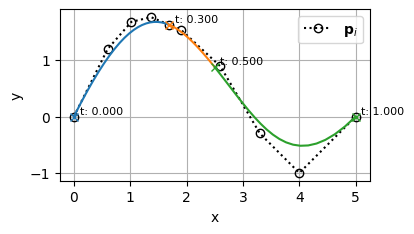
こんな感じで、曲線の形状を維持したまま、\(t=0.3\)を境に、曲線を完全に独立した2つのセグメントに分けることができた
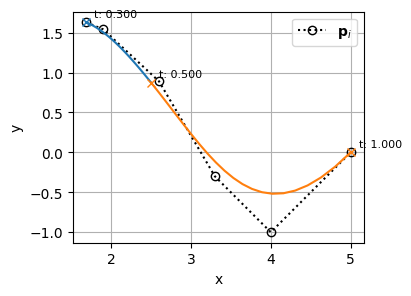
さらにこれを
\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.3,~ 0.3,~ 0.3,~ 0.3,~ 0.3] \\
m &= 10 \\
n &= m - (k + 1) = 10 - 5 = 5 \\
\end{align}
\begin{align}
k &= 4 \\
\mathbf{t} &= [0.3,~ 0.3,~ 0.3,~ 0.3,~ 0.3,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}
という2つのBSpline曲線(\(t=0.3\)で\(k+1\)個の多重端末ノット)だと考えると、もともと10個あった制御点\(\mathbf{P}=\mathbf{p}_0,~ \cdots,~ \mathbf{p}_9\)の5番目(\(\mathbf{p}_4\))を共通として、2つのBSpline曲線として再定義することも可能になる
楽しくなってきた
- 任意の位置にk個のノットを挿入することで、BSpline曲線を任意の位置で分割することができる
- 分割した曲線は、ノット挿入位置に対応する制御点を端点とした2つのBSpline曲線として再定義できる
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
np.set_printoptions(formatter={'float':'{:3.2f}'.format}, linewidth=999)
# ===== set parameter (t, c, k) =====
k = 4
t_add = 0.3
c = np.array([[0, 0], [1, 2], [2, 2], [3, 0], [4, -1],[5, 0]])
n = len(c)
m = n + (k + 1)
t = [0] * k + np.linspace(0, 1, m - 2 * k).tolist() + [1] * k
# ===== get bspline =====
bspline0 = MyBSpline(t, c, k)
print('\noriginal:\n')
print(' t:', bspline0.t)
print(' c.shape:', bspline0.c.shape)
print(' k:', bspline0.k)
plot_bspline(bspline0)
# ===== insert knot =====
bspline1 = bspline0.insert_knot(x=t_add, m=k)
print('\ninsert knot:\n')
print(' t:', bspline1.t)
print(' c.shape:', bspline1.c.shape)
print(' k:', bspline1.k)
plot_bspline(bspline1)
# ===== split c and t =====
m2 = len(bspline1.t) - (bspline1.t[::-1].tolist().index(t_add)) # t_addが出てくる最後のインデックスから前半のノットベクトルの長さを取得
t2 = bspline1.t[:m2].tolist() + [t_add]
n2 = len(t2) - (k+1)
c2 = bspline1.c[:n2]
print('\nbspline2:\n')
print(' t:', t2)
print(' c.shape:', c2.shape)
m3 = len(bspline1.t) - (bspline1.t.tolist().index(t_add)) # t_addが出てくる最初のインデックスから後半のノットベクトルの長さを取得
t3 = [t_add] + bspline1.t[-m3:].tolist()
n3 = len(t3) - (k+1)
c3 = bspline1.c[-n3:]
print('\nbspline3:\n')
print(' t:', t3)
print(' c.shape:', c3.shape)
# ===== re-difine split bspline =====
bspline2 = MyBSpline(t2, c2, k)
bspline3 = MyBSpline(t3, c3, k)
plot_bspline(bspline2)
plot_bspline(bspline3)
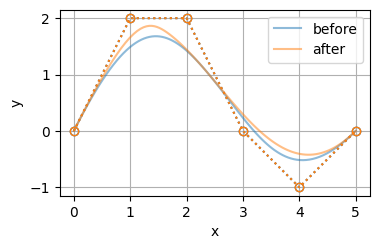
plot([bspline0, bspline2, bspline3], alpha=0.8, labels=['original', 'split0', 'split1', ])
insert knot:
t: [0.00 0.00 0.00 0.00 0.00 0.30 0.30 0.30 0.30 0.50 1.00 1.00 1.00 1.00 1.00]
c.shape: (10, 2)
k: 4
bspline2:
t: [0.0, 0.0, 0.0, 0.0, 0.0, 0.3, 0.3, 0.3, 0.3, 0.3]
c.shape: (5, 2)
bspline3:
t: [0.3, 0.3, 0.3, 0.3, 0.3, 0.5, 1.0, 1.0, 1.0, 1.0, 1.0]
c.shape: (6, 2)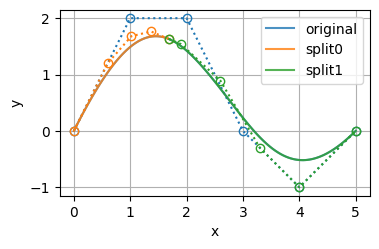
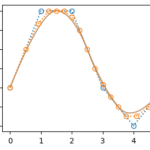
BSpline曲線の結合
BSpline曲線の分割と逆の操作を行えば、2つのBSpline曲線を結合することができる
2つのBSpline曲線(添え字 \(\text{□}_0\)、\(\text{□}_1\))が結合できる条件は以下の通り:
- 結合される端位置での制御点座標が同じ(\(\mathbf{p_0}_{n-1}=\mathbf{p_1}_{0}\))
- 結合される端位置での多重端末ノットの値が同じ(\(\mathbf{t_0}_{m-1}=\mathbf{t_1}_{0}\))
- 階数が同じ(\(k_0=k_1\))
具体的な手順は以下の通り:
- ノットベクトルの振り直しを使って2つのBSpline曲線のノットベクトルが繋がるようにする
- 次数上げを使って2つのBSpline曲線の階数をそろえる
- 1つ目のBSpline曲線の終点と2つ目のBSpline曲線の始点を共通として、ノットベクトルと制御点をそれぞれ結合する
例えば、以下の2つのBSpline曲線:
\begin{align}
& \begin{cases}
k_0 &= 1 \\
\mathbf{t_0} &= [0,~ 0,~ 0.5,~ 1,~ 1] \\
m_0 &= 5 \\
n_0 &= m_0 - (k_0 + 1) = 5 - 2 = 3 \\
\end{cases} \\\\
& \begin{cases}
k_1 &= 4 \\
\mathbf{t_1} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m_1 &= 11 \\
n_1 &= m_1 - (k_1 + 1) = 11 - 5 = 6 \\
\end{cases}
\end{align}
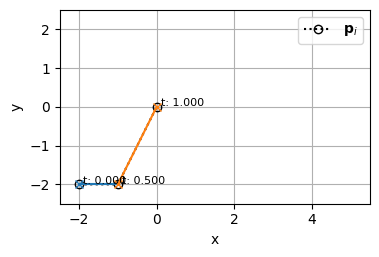
bspline0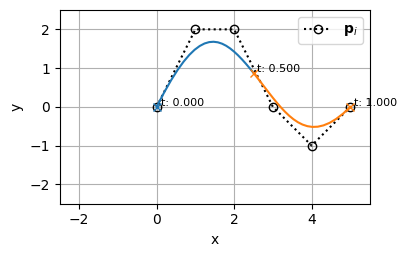
bspline1を結合してみる
ちなみに、制御点座標は\(\mathbf{p_0}_{2}=\mathbf{p_1}_{0}=(0,~ 0)\)としている
1. ノットベクトルを振り直す
2つ目のBSpline曲線のノットベクトルを振り直す
\begin{align}
& \begin{cases}
\mathbf{t_0} = [0,~ 0,~ 0.5,~ 1,~ 1] \\
\mathbf{t_1} = [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1]
\end{cases} \\\\
\rightarrow \qquad & \begin{cases}
\mathbf{t_0} = [0,~ 0,~ 0.25,~ 0.5,~ 0.5] \\
\mathbf{t_1} = [0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.75,~ 1,~ 1,~ 1,~ 1,~ 1]
\end{cases}
\end{align}
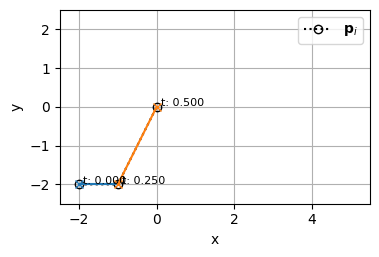
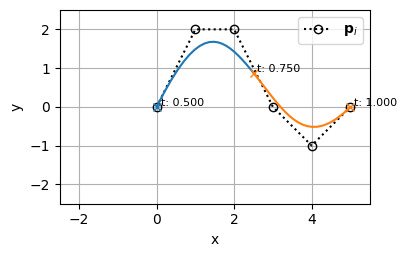
2. 階数をそろえる
階数が\(k=1\)の方のBSpline曲線の階数を\(k=4\)まであげる
\begin{align}
\begin{cases}
k_0 = 1 \\
m_0 = 5 \\
n_0 = m_0 - (k_0 + 1) = 3 \\
\end{cases}
\rightarrow
\begin{cases}
k_0 = 4 \\
m_0 = 14 \\
n_0 = m_0 - (k_0+1) = 9 \\
\end{cases}
\end{align}
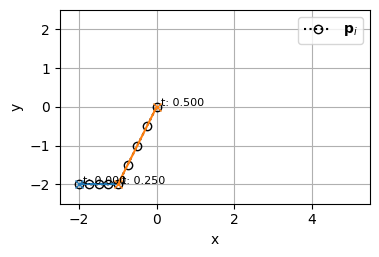
3. 結合する
1つ目のBSpline曲線の終点と2つ目のBSpline曲線の始点を共通として新たなノットベクトルと制御点群を生成し、BSpline曲線を定義する
\begin{align}
& \begin{cases}
\mathbf{t_0} = [0,~ 0,~ 0,~ 0,~ 0,~ 0.25,~ 0.25,~ 0.25,~ 0.25,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.5] \\
\mathbf{t_1} = [0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.75,~ 1,~ 1,~ 1,~ 1,~ 1]
\end{cases} \\ \\
\rightarrow \qquad &
\mathbf{t_{marged}} = [0,~ 0,~ 0,~ 0,~ 0,~ 0.25,~ 0.25,~ 0.25,~ 0.25,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 0.75,~ 1,~ 1,~ 1,~ 1,~ 1]
\end{align}
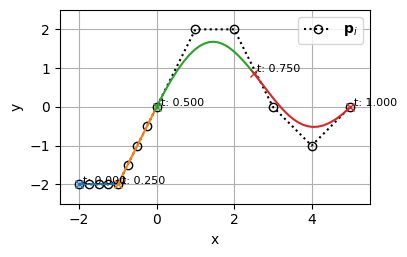
これで2つのBSpline曲線を結合することができた
- BSpline曲線は結合することもできる。
- 手順は、ノットを振りなおす → 階数をそろえる → ノットベクトルと制御点をつなげる
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
np.set_printoptions(formatter={'float':'{:3.2f}'.format}, linewidth=999)
# ===== set parameter (t, c, k) =====
k = 1
t_add = 0.3
c = np.array([[-2, -2], [-1, -2], [0, 0]])
n = len(c)
m = n + (k + 1)
t = [0] * k + np.linspace(0, 1, m - 2 * k).tolist() + [1] * k
# ===== get bspline0 =====
bspline0 = MyBSpline(t, c, k)
# ===== set parameter (t, c, k) =====
k = 4
c = np.array([[0, 0], [1, 2], [2, 2], [3, 0], [4, -1],[5, 0]])
n = len(c)
m = n + (k + 1)
t = [0] * k + np.linspace(0, 1, m - 2 * k).tolist() + [1] * k
# ===== get bspline1 =====
bspline1 = MyBSpline(t, c, k)
# ===== plot =====
x_range, y_range = (-2.5, 5.5), (-2.5, 2.5)
print('\nbspline0:\n')
print(' t:', bspline0.t)
print(' c.shape:', bspline0.c.shape)
print(' k:', bspline0.k)
plot_bspline(bspline0, x_range=x_range, y_range=y_range)
print('\nbspline1:\n')
print(' t:', bspline1.t)
print(' c.shape:', bspline1.c.shape)
print(' k:', bspline1.k)
plot_bspline(bspline1, x_range=x_range, y_range=y_range)bspline0:
t: [0.00 0.00 0.50 1.00 1.00]
c.shape: (3, 2)
k: 1
bspline1:
t: [0.00 0.00 0.00 0.00 0.00 0.50 1.00 1.00 1.00 1.00 1.00]
c.shape: (6, 2)
k: 4# ===== reset t =====
t0_new = bspline0.t * 0.5 # [0, 1] -> [0, 0.5]
bspline0 = MyBSpline(t0_new, bspline0.c, bspline0.k)
t1_new = bspline1.t * 0.5 + 0.5 # [0, 1] -> [0.5, 1.0]
bspline1 = MyBSpline(t1_new, bspline1.c, bspline1.k)
# ===== plot =====
print('\nbspline0:\n')
print(' t:', bspline0.t)
plot_bspline(bspline0, x_range=x_range, y_range=y_range)
print('\nbspline1:\n')
print(' t:', bspline1.t)
plot_bspline(bspline1, x_range=x_range, y_range=y_range)bspline0:
t: [0.00 0.00 0.25 0.50 0.50]
bspline1:
t: [0.50 0.50 0.50 0.50 0.50 0.75 1.00 1.00 1.00 1.00 1.00]# ===== degree elevation =====
tmp = bspline0.degree_elevation(k_target=4)
bspline0 = MyBSpline(tmp.t, tmp.c, tmp.k)
print('\ndegree elevation:\n')
print(' t:', bspline0.t)
print(' c.shape:', bspline0.c.shape)
print(' k:', bspline0.k)
plot_bspline(bspline0, x_range=x_range, y_range=y_range)degree elevation:
t: [0.00 0.00 0.00 0.00 0.00 0.25 0.25 0.25 0.25 0.50 0.50 0.50 0.50 0.50]
c.shape: (9, 2)
k: 4# ===== marge bspline =====
t_marge = bspline0.t[:-(bspline0.k+1)].tolist() + bspline1.t[1:].tolist()
c_marge = np.concatenate([bspline0.c[:-1], bspline1.c])
bspline = MyBSpline(t_marge, c_marge, bspline0.k)
print('\nmarge:\n')
print(' t:', bspline.t)
print(' c.shape:', bspline.c.shape)
print(' k:', bspline.k)
plot_bspline(bspline, x_range=x_range, y_range=y_range)
plot_basis_matrix(bspline)marge:
t: [0.00 0.00 0.00 0.00 0.00 0.25 0.25 0.25 0.25 0.50 0.50 0.50 0.50 0.75 1.00 1.00 1.00 1.00 1.00]
c.shape: (14, 2)
k: 4中間曲線の生成
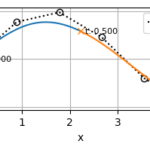
ノットベクトルと階数が共通なBSpline曲線は、制御点の座標を混ぜ合わせることで中間曲線を作ることができる
つまり、ノットベクトルと階数が同じ(=基底関数が同じ)2つのBSpline曲線があったとき:
\begin{align}
& \begin{cases}
\mathbf{c_0}(u) = \sum_{i=0}^{n-1} N_{i, k}(u) \mathbf{p_0}_i \\\\
\mathbf{c_1}(u) = \sum_{i=0}^{n-1} N_{i, k}(u) \mathbf{p_1}_i
\end{cases}
\end{align}
中間曲線は係数\(\alpha\)を用いて次のように表すことができる
\begin{align}
\mathbf{c}(u) & = (1-\alpha)\, \mathbf{c_0}(u) + \alpha\, \mathbf{c_1}(u) \\ \\
& = (1-\alpha)\, \left(\sum_{i=0}^{n-1} N_{i, k}(u) \mathbf{p_0}_i\right) + \alpha\, \left(\sum_{i=0}^{n-1} N_{i, k}(u) \mathbf{p_1}_i\right) \\ \\
& = \sum_{i=0}^{n-1} N_{i, k}(u) \left\{ (1-\alpha)\, \mathbf{p_0} + \alpha\, \mathbf{p_1}\right\}
\end{align}
具体的な手順は以下の通り
- 次数上げで階数をそろえる
- ノットの挿入でノットベクトルを同じにする
- 制御点を混ぜ合わせる
例えば、以下の2つのBSpline曲線:
\begin{align}
& \begin{cases}
k_0 &= 1 \\
\mathbf{t_0} &= [0,~ 0,~ 0.5,~ 1,~ 1] \\
m_0 &= 5 \\
n_0 &= m_0 - (k_0 + 1) = 5 - 2 = 3 \\
\end{cases} \\\\
& \begin{cases}
k_1 &= 4 \\
\mathbf{t_1} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m_1 &= 11 \\
n_1 &= m_1 - (k_1 + 1) = 11 - 5 = 6 \\
\end{cases}
\end{align}
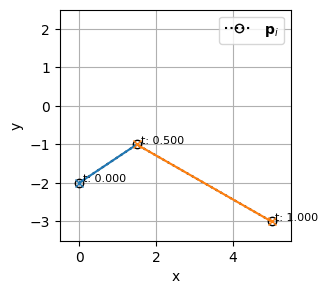
bspline0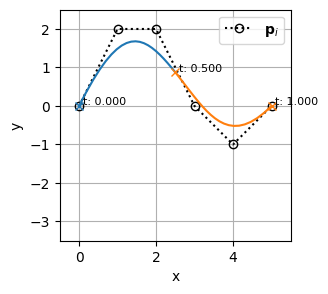
bspline1の中間曲線を生成してみる
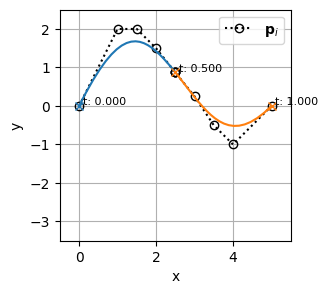
1. 次数上げで階数をそろえる
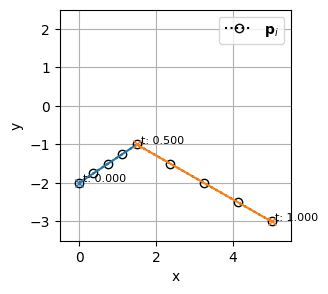

bspline1(そのまま)2. ノットの挿入でノットベクトルを同じにする

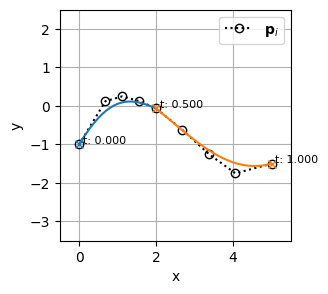
bspline1(ノット挿入後)3. 制御点を混ぜ合わせる
\begin{align}
\mathbf{p} & = (1-\alpha)\, \mathbf{p_0} + \alpha\, \mathbf{p_1}
\end{align}
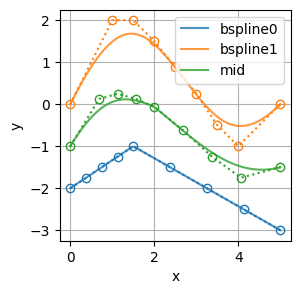
これで2つのBSpline曲線の中間曲線を生成することができた
- BSpline曲線はノットベクトルと階数をそろえれば、制御点を混ぜ合わせることで中間曲線を生成できる
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
np.set_printoptions(formatter={'float':'{:3.2f}'.format}, linewidth=999)
# ===== set parameter (t, c, k) =====
k = 1
t_add = 0.5
c = np.array([[0, -2], [1.5, -1], [5, -3]])
n = len(c)
m = n + (k + 1)
t = [0] * k + np.linspace(0, 1, m - 2 * k).tolist() + [1] * k
# ===== get bspline0 =====
bspline0 = MyBSpline(t, c, k)
# ===== set parameter (t, c, k) =====
k = 4
c = np.array([[0, 0], [1, 2], [2, 2], [3, 0], [4, -1],[5, 0]])
n = len(c)
m = n + (k + 1)
t = [0] * k + np.linspace(0, 1, m - 2 * k).tolist() + [1] * k
# ===== get bspline1 =====
bspline1 = MyBSpline(t, c, k)
# ===== plot =====
x_range, y_range = (-0.5, 5.5), (-3.5, 2.5)
print('\nbspline0:\n')
print(' t:', bspline0.t)
print(' c.shape:', bspline0.c.shape)
print(' k:', bspline0.k)
plot_bspline(bspline0, x_range=x_range, y_range=y_range)
print('\nbspline1:\n')
print(' t:', bspline1.t)
print(' c.shape:', bspline1.c.shape)
print(' k:', bspline1.k)
plot_bspline(bspline1, x_range=x_range, y_range=y_range)bspline0:
t: [0.00 0.00 0.50 1.00 1.00]
c.shape: (3, 2)
k: 1
bspline1:
t: [0.00 0.00 0.00 0.00 0.00 0.50 1.00 1.00 1.00 1.00 1.00]
c.shape: (6, 2)
k: 4# ===== degree elevation =====
tmp = bspline0.degree_elevation(k_target=4)
bspline0 = MyBSpline(tmp.t, tmp.c, tmp.k)
print('\ndegree elevation:\n')
print(' t:', bspline0.t)
print(' c.shape:', bspline0.c.shape)
print(' k:', bspline0.k)
plot_bspline(bspline0, x_range=x_range, y_range=y_range)
# ===== insert knot =====
bspline1 = bspline1.insert_knot(x=t_add, m=k-1)
print('\ninsert knot:\n')
print(' t:', bspline1.t)
print(' c.shape:', bspline1.c.shape)
print(' k:', bspline1.k)
plot_bspline(bspline1, x_range=x_range, y_range=y_range)degree elevation:
t: [0.00 0.00 0.00 0.00 0.00 0.50 0.50 0.50 0.50 1.00 1.00 1.00 1.00 1.00]
c.shape: (9, 2)
k: 4
insert knot:
t: [0.00 0.00 0.00 0.00 0.00 0.50 0.50 0.50 0.50 1.00 1.00 1.00 1.00 1.00]
c.shape: (9, 2)
k: 4# ===== mid curve =====
alpha = 0.5
c_mid = (1-alpha) * bspline0.c + alpha * bspline1.c
bspline = MyBSpline(bspline0.t, c_mid, bspline0.k)
print('\nmid:\n')
print(' t:', bspline.t)
print(' c.shape:', bspline.c.shape)
print(' k:', bspline.k)
plot_bspline(bspline, x_range=x_range, y_range=y_range)mid:
t: [0.00 0.00 0.00 0.00 0.00 0.50 0.50 0.50 0.50 1.00 1.00 1.00 1.00 1.00]
c.shape: (9, 2)
k: 4おわりに
BSpline曲線について、知っておくと便利な基本的な操作について説明した
これである程度自由自在にBSpline曲線を操れるようになったので、いよいよ所望のBSpline曲線の生成を行っていきたいと思う

↓まとめ



コメント