BSpline曲線の定式化と基本的な性質

BSpline曲線の定式化と基本的な性質について説明する

はじめに
BSpline曲線の定式化
行列形式
BSpline曲線の基底関数
BSpline曲線の微分
簡単なBSpline曲線
最小制御点数のBSpline曲線
階数k=1のBSpline曲線
多重ノットを持つBSpline曲線
BSpline曲線の階数と次数
おわりに

はじめに

BSpline曲線とは、言わずと知れた「滑らかな曲線」を作る技術である

工学の世界では主にCADなどに用いられ、世界中のエンジニアの手元で日夜あらゆる滑らかな曲線を生成している

この記事では、BSpline曲線の定式化と基本的な性質について数値例や定式化も含めて解説する

この記事で使うような技術を使ってBSpline曲線そのものをこねくり回す機会はあまりないかもしれないが、CADで滑らかな曲線を自在に描けるようになりたい人たちの一助になれば幸いである

↓参考文献

リンク

↓プログラムの実装

なお、この記事の数式に付されている式番号は、この参考文献の式番号と対応するようにしている

それではいっていみよう

BSpline曲線の定式化

BSpline曲線は以下の式で表される。

\begin{align}
\mathbf{c}(u) = \sum_{i=0}^{n-1} N_{i,k}(u) \, \mathbf{p}_i
\tag{4.2.1}
\end{align}

\begin{align}
\mathbf{c}(u)=\left[\begin{matrix} x_c(u) \\ y_c(u) \\ z_c(u) \end{matrix}\right],
\qquad
\mathbf{p}_i=\left[\begin{matrix} x_{p_i} \\ y_{p_i} \\ z_{p_i} \end{matrix}\right],
\qquad i=0,~ 1,~ \cdots,~ n-1
\end{align}

ここで、\(\mathbf{c}(u)\)はBSpline曲線を構成する座標点、\(u\)はBSpline曲線の始点から終点までを繋ぐパラメータ、\(N_{i,k}(u)\)はBSpline基底関数、\(\mathbf{p}_i\)はBSpline曲線の形を決定する\(n\)個の制御点である。

ただ、流石にこれだけではなんのこっちゃわからないので、総和の\(\sum\)を書き下してみる

\begin{align}
\mathbf{c}(u) = N_{0, k}(u) \, \mathbf{p}_0 + N_{1, k}(u) \, \mathbf{p}_1 + \cdots + N_{n-1, k}(u) \, \mathbf{p}_{n-1}
\end{align}

すると、BSpline曲線とは「\(n\)個の制御点\(\mathbf{p}_i\)を基底関数\(N_{i,k}(u)\)で重み付けして生み出された点\(\mathbf{c}(u)\)の集まり」であることがわかってくる。

最も簡単な2点間の座標の線形補間として

\begin{align}
\mathbf{c}(u) = (1 - u) \, \mathbf{p}_0 + u \, \mathbf{p}_1,~ \qquad 0 \leq u \leq 1
\end{align}

という式があるが、BSpline曲線はこの式を複数の点に拡張し、なにやら\(N_{i,k}(u)\)という複雑な補間式を使うことで最上級まで進化させたものだと考えればいい。

ちなみに、基底関数\(N_{i,k}(u)\)は各制御点\(\mathbf{p}_i\)に対応した重み関数なので、パラメータ\(u\)において以下の性質を持つ：

\begin{align}
\sum_{i=0}^{n-1} N_{i,k}(u) = 1,~ \qquad
0 \leq N_{i,k}(u) \leq 1
\end{align}

ここまでのポイント

BSpline曲線\(\mathbf{c}(u)\)は、\(n\)個の制御点\(\mathbf{p}_i\)を基底関数\(N_{i,k}(u)\)で重みづけして足し合わせることで定義されている

行列形式

なんとなく数式全体の形が見えてきたので、今度は離散的な\(l\)個のパラメータ\(u=u_0,~ u_1,~ \cdots,~ u_{l-1}\)を与えて行列形式に書き下してみる（曲線を点群で表すイメージ）

\begin{align}
\begin{bmatrix}
\mathbf{c}(u_0) \\
\mathbf{c}(u_1) \\
\vdots \\
\mathbf{c}(u_{l-1})
\end{bmatrix}
&=
\begin{bmatrix}
N_{0,k}(u_0) & N_{1,k}(u_0) & \cdots & N_{n-1,k}(u_0) \\
N_{0,k}(u_1) & N_{1,k}(u_1) & \cdots & N_{n-1,k}(u_1) \\
\vdots & \vdots & \ddots & \vdots \\
N_{0,k}(u_{l-1}) & N_{1,k}(u_{l-1}) & \cdots & N_{n-1,k}(u_{l-1})
\end{bmatrix}
\begin{bmatrix}
\mathbf{p}_0 \\
\mathbf{p}_1 \\
\vdots \\
\mathbf{p}_{n-1}\end{bmatrix}
\end{align}

ここで、

\begin{align}
\mathbf{C} &=
\begin{bmatrix}
\mathbf{c}(u_0) \\
\mathbf{c}(u_1) \\
\vdots \\
\mathbf{c}(u_{l-1})
\end{bmatrix} \\ \\
\mathbf{N} &=
\begin{bmatrix}
N_{0,k}(u_0) & N_{1,k}(u_0) & \cdots & N_{n-1,k}(u_0) \\
N_{0,k}(u_1) & N_{1,k}(u_1) & \cdots & N_{n-1,k}(u_1) \\
\vdots & \vdots & \ddots & \vdots \\
N_{0,k}(u_{l-1}) & N_{1,k}(u_{l-1}) & \cdots & N_{n-1,k}(u_{l-1})
\end{bmatrix} \\ \\
\mathbf{P} &=
\begin{bmatrix}
\mathbf{p}_0 \\
\mathbf{p}_1 \\
\vdots \\
\mathbf{p}_{n-1}\end{bmatrix}
\end{align}

とすると

\begin{align}
\mathbf{C} &= \mathbf{N}\, \mathbf{P}
\end{align}

となり、\(\mathbf{c}_i\)、\(\mathbf{p}_i\)が3次元座標のとき、BSpline曲線の座標点群\(\mathbf{C}\)は\((l,~ 3)\)の行列、基底関数\(\mathbf{N}\)は\((l,~ n)\)の行列、制御点\(\mathbf{P}\)は\((n,~ 3)\)の行列であることがわかる。

\begin{align}
\mathbf{C} = \mathbf{N}\, \mathbf{P} \quad
\rightarrow \quad (l,~ 3) = (l,~ n) \, \times \, (n,~ 3)
\end{align}

よって、BSpline曲線の座標は基底関数行列と制御点の行列演算で求められることが分かった（プログラミングと相性が良さそうだということがわかる）

ここまでのポイント

BSpline曲線の定義は行列演算でも表現できる

それでは次は、BSpline曲線の重み付け関数である「基底関数」について詳しくみてみよう

BSpline曲線の基底関数

パラメータ\(u\)におけるBSpline曲線の基底関数\(N_{i,k}(u)\)は、de Boor Coxの漸化式と呼ばれる式で再帰的に定義される。

\begin{align}
N_{i,k}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,k-1}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(u) \\\\
N_{i,0}(u) &=
\begin{cases}
1 & t_i \leq u < t_{i+1} \\
0 & \text{otherwise}
\end{cases},~ \qquad i=0,~ 1,~ \cdots n-1 \\
\tag{4.1.1}
\end{align}

横軸にパラメータuをとると、一般的な基底関数はこんな形のグラフになる

BSpline曲線の基底関数\(N_{i,k}(u)\)は、パラメータ\(u\)のほかに、新たな2つの変数\(k\)と\(t\)を使って定義されている

まず、\(k\)は階数と呼ばれる整数のスカラーで、以下の点を押さえておけばいい

BSpline曲線は\(k-1\)階までの微分が連続になる
人間が「滑らか」だと感じるのは2階微分（曲率）が連続のときなので、2階微分が連続になる\(k=3\)や\(k=4\)がよく用いられる。
\(k=1\)にすると1階微分（曲線の傾き）すら不連続になるので、BSpline曲線は折れ線になる。
\(k\)を大きくすれば大きくするほど高次の微分まで連続になるが、曲線の表現力が強くなりすぎて曲線がうねるようになる（オーバーフィッティング）。
制御点の数\(n\)は\(k+1\)以上でなければならない
\begin{align}n≧k+1\end{align}

また、\(\mathbf{t}\)はノットベクトルといい、以下に示すような離散的な1次元配列である。

\begin{align}
\mathbf{t} = \left[t_0,~ t_1,~ t_2,~ \cdots,~ t_{m-1}\right],~ \qquad m=n+(k+1)
\end{align}

ノットベクトルはBSpline曲線の肝になる重要な要素だが、いかんせん直感的な理解が難しいので、ひとまず次のポイントを押さえておけばいい。

ノットベクトルの長さ\(m\)は、制御点の数\(n\)と階数\(k\)から一意に決まる
\begin{align}m=n+(k+1)\end{align}
→ scipy.interpolate.BSplineでは、\(m\), \(n\), \(k\)が上記の関係を満たしていないとエラーが出る
ノットベクトルはどんな値を取ってもいい（整数、無理数、負の値、他）
ノットベクトルは同じ値を連続させてもいい。
ただし、ノットベクトルは単調増加でなくてはならない。
BSpline曲線\(\mathbf{c}(u)\)は、ノットベクトルの最小値\(t_0\)と最大値\(t_{m-1}\)の間のパラメータ\(u =[t_0,~ t_{m-1}]\)で定義される
→ ノットベクトルを\(t_0=0\), \(t_{m-1}=1\)の範囲で定義しておくと、BSpline曲線は始点でパラメータ\(u=0\)、終点でパラメータ\(u=1\)となるので楽。
ノットベクトルの最初と最後の要素を\(k＋1\)回連続させると、最初の制御点から始まり、最後の制御点で終わる曲線になる（多重端末ノット）。便利なので基本的に多重端末ノットが使われる。

まとめると、例えば\(k=3\)、\(m=11\)、多重端末ノットのノットベクトルはこんな感じになる

\begin{align}
t &= [0,~ 0,~ 0,~ 0,~ 0.25,~ 0.5,~ 0.75,~ 1,~ 1,~ 1,~ 1]
\end{align}

ノットベクトルについてはまだまだ大事な性質がいくつもあるが、細かい点についてはおいおい説明する。

ここまでのポイント

基底関数は、ノットベクトル\(\mathbf{t}\)と階数\(k\)によって計算される。
BSpline曲線は\(k-1\)階微分まで連続になる
通常は\(k=3\)か\(k=4\)が使われる。\(k=1\)だと折れ線になり、\(k \geq 5\)になると曲線がうねりはじめる。
制御点の数は\(n≧k+1\)でなければならない
ノットベクトルの長さは\(m=n+k+1\)で一意に決まる
ノットベクトルは0からはじまり1で終わる単調増加の数列にする。
最初と最後のノットを\(k+1\)個並べると、始点と終点は制御点を通るようになる（多重端末ノット）。

BSpline曲線の微分

ここで、BSpline曲線の微分の連続性について話が出てきたので、BSpline曲線の微分についても説明しておく。

あらためて、BSpline曲線\(\mathbf{c}(u)\)は以下の式で表される。

\begin{align}
\mathbf{c}(u) = \sum_{i=0}^{n-1} N_{i,k}(u) \, \mathbf{p}_i
\tag{4.2.1}
\end{align}

BSpline曲線\(\mathbf{c}(u)\)はパラメータ\(u\)に対する1変数関数なので、\(u\)について微分することができる。

両辺を\(u\)で微分すると、以下のようになる

\begin{align}
\frac{d^{r}\mathbf{c}(u)}{du^{r}} = \sum_{i=0}^{n-1} \frac{d^{r}N_{i,k}(u)}{du^{r}} \, \mathbf{p}_i
\end{align}

制御点\(\mathbf{p}_i\)はユーザーから与えられる定数で\(\frac{d\mathbf{p}_i}{du}=0\)なので、BSpline曲線のr階微分\(\frac{d^{r}\mathbf{c}(u)}{du^{(r)}}\)は、基底関数行列のr階微分\(\frac{d^{(r)}N_{i,k}(u)}{du^{r}}\)に制御点\(\mathbf{p}_i\)をかけるだけになっている

さらに、BSpline曲線の基底関数であるde Boor Coxの漸化式のr階微分は、同じく漸化式で以下のように計算できる

\begin{align}
N_{i,k}^{(r)}(u) =\frac{k-1}{t_{i+k} - t_i} \cdot N_{i,k-1}^{(r-1)}(u)-\frac{k-1}{t_{i+k+1} - t_{i+1}} \cdot N_{i+1,k-1}^{(r-1)}(u)
\end{align}

ここで、

\begin{align}
N_{i,k}^{(r)}(u) &= \frac{d^r}{dt^r} N_{i,k}(u)
\\ \\
N_{i,k}^{(0)}(u) &= N_{i,k}(u)
\end{align}

楽ちんである

ポイント

BSpline曲線のr階微分は、基底関数のr階微分\(N_{i,k}^{(r)}(u)\)と制御点\(\mathbf{p}_i\)の行列演算で計算できる
基底関数（de Boor Coxの漸化式）のr階微分\(N_{i,k}^{(r)}(u)\)は解析的に計算できる

ここまででBSpline曲線の基本的なポイントは抑えることができたので、これからは具体的な例を見ながらBSpline曲線について説明していく

簡単なBSpline曲線

まずは簡単なBSpline曲線を考えてみる。

\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}

ノットベクトルは始点と終点の値をそれぞれ \(k + 1 = 5\) 回ずつ重ねた多重端末ノットである。

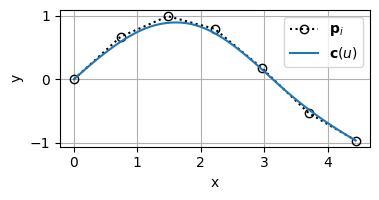
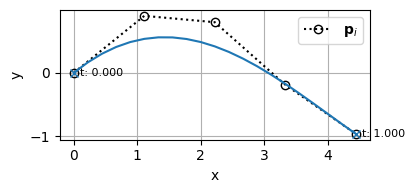
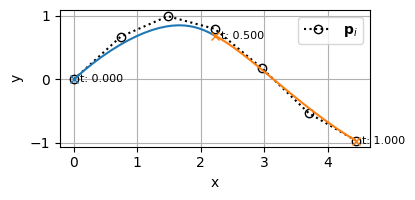
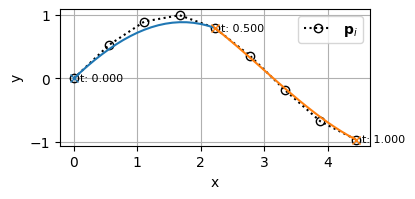
適当な制御点群\(\mathbf{P}=[\mathbf{p}_0,~ \mathbf{p}_1,~ \cdots,~ \mathbf{p}_5]\)を与えてBSpline曲線を描くと次のようになる。

多重端末ノットの効果

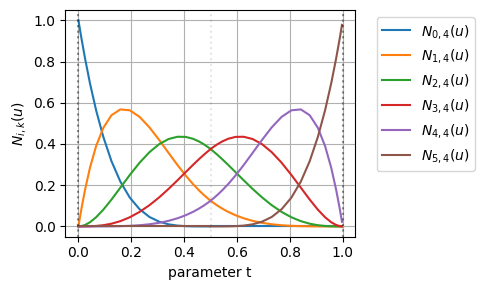
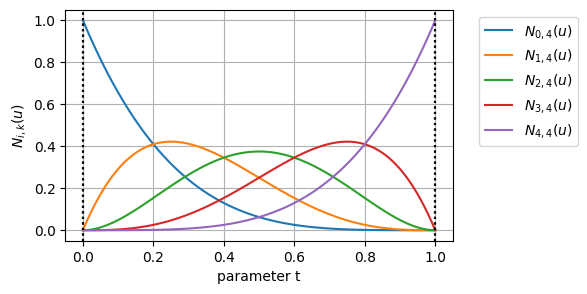
横軸にパラメータ、縦軸に基底関数をとったグラフはこんな感じになる

基底関数のグラフを見てみると、多重端末ノットを採用しているため、始点\(u=0\)では制御点\(\mathbf{p}_0\)に対応する基底関数\(N_{0,4}(0)\)のみが1になっており、終点\(u=1\)では制御点\(\mathbf{p}_5\)に対応する基底関数\(N_{5,4}(1)\)のみが1になっている

BSpline曲線の定義式に照らし合わせると

\begin{cases}
\mathbf{c}(0) &= \sum_{i=0}^{n-1} N_{i,k}(0) \, \mathbf{p}_i = N_{0,4}(0) \, \mathbf{p}_0 = \mathbf{p}_0 \\ \\
\mathbf{c}(1) &= \sum_{i=0}^{n-1} N_{i,k}(1) \, \mathbf{p}_i = N_{5,4}(1) \, \mathbf{p}_5 = \mathbf{p}_5 \\
\end{cases}

であり、「多重端末ノットを使うと始点と終点は制御点を通るようになる」という性質を満たしていることが分かる。

ちなみに、多重端末ノットに対して、それ以外のノットを内部ノットという

BSpline曲線のセグメント

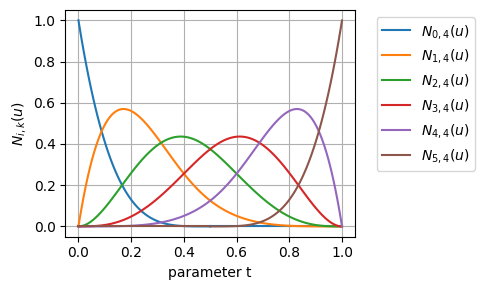
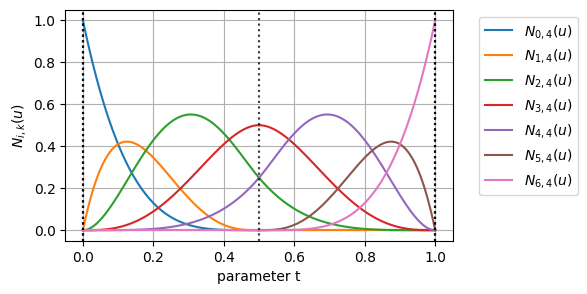
次に、基底関数のグラフの横軸に、ノットベクトルの位置を黒破線で追加してみる

\begin{align}
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1]
\end{align}

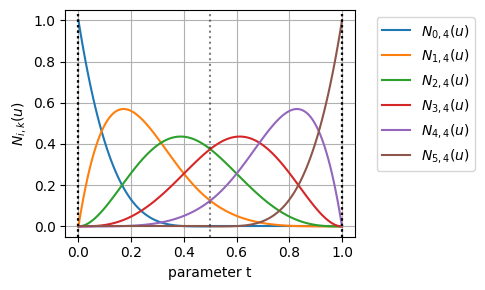
これを見てみると、

\(0 \leq u \leq 0.5\)の範囲では、制御点\(\mathbf{p}_0\)から制御点\(\mathbf{p}_4\)に対応する基底関数が非ゼロになっている
\(0.5 \leq u \leq 1\)の範囲では、制御点\(\mathbf{p}_1\)から制御点\(\mathbf{p}_5\)に対応する基底関数が非ゼロになっている

ことが分かる

BSpline曲線の定義式に照らし合わせると

\begin{cases}
\mathbf{c}(u) &= N_{0,k}(u) \, \mathbf{p}_0 + & N_{1,k}(u) \, \mathbf{p}_1 + \cdots + N_{4,k}(u) \, \mathbf{p}_4 & & \qquad 0 \leq u \leq 0.5 \\ \\
\mathbf{c}(u) &= & N_{1,k}(u) \, \mathbf{p}_1 + \cdots + N_{4,k}(u) \, \mathbf{p}_4 & + N_{5,k}(u) \, \mathbf{p}_5 & \qquad 0.5 \leq u \leq 1.0 \\ \\
\end{cases}

であり、パラメータ\(u=0.5\)を境に曲線の元となる制御点が更新され、曲線が2つのセグメントに分かれていることが分かる

つまり、ノットベクトルには以下の性質がある

BSpline曲線\(\mathbf{c}(u)\)は、ノットベクトル\(\mathbf{t}=[t_0,~ t_1,~ \cdots,~ t_{m-1}]\)によって、\(u=[t_j,~ t_{j+1}]\)のセグメントに分割される
1つのセグメントに対しては、\(k+1\)個の制御点が重ね合わされて曲線を作っている
→ 逆にそれ以外の制御点の影響は受けないので、セグメントごとに局所的な曲線の調整が可能になる

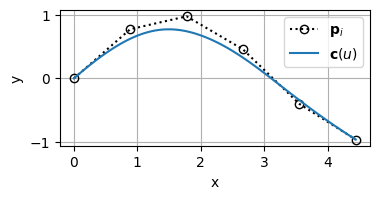
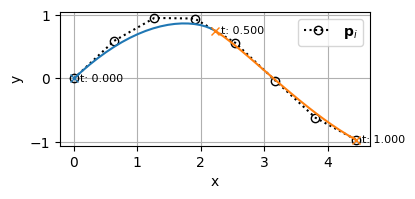
ちなみにBSpline曲線をセグメントで色分けしてみるとこんな感じになる

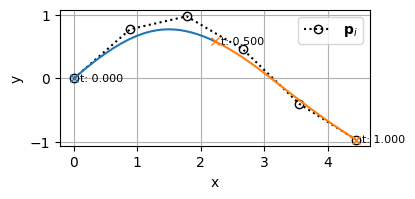
セグメントの違いが分かりやすくなった

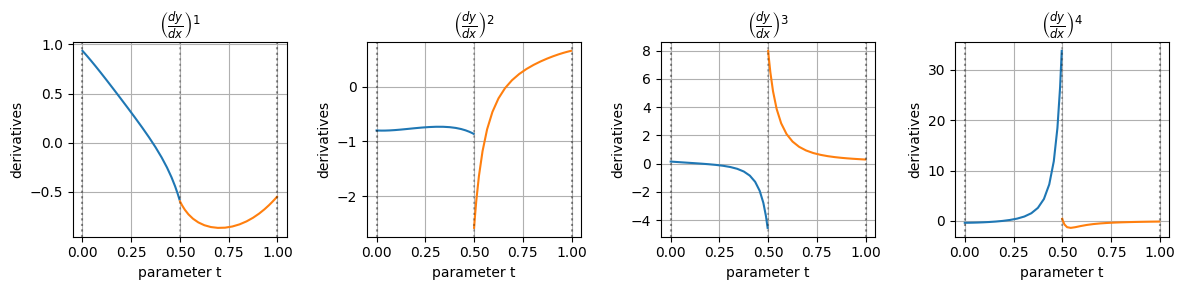
BSpline曲線の微分

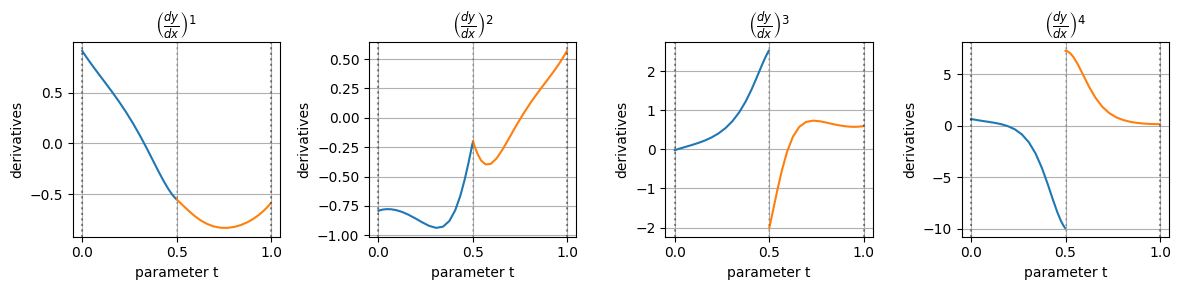
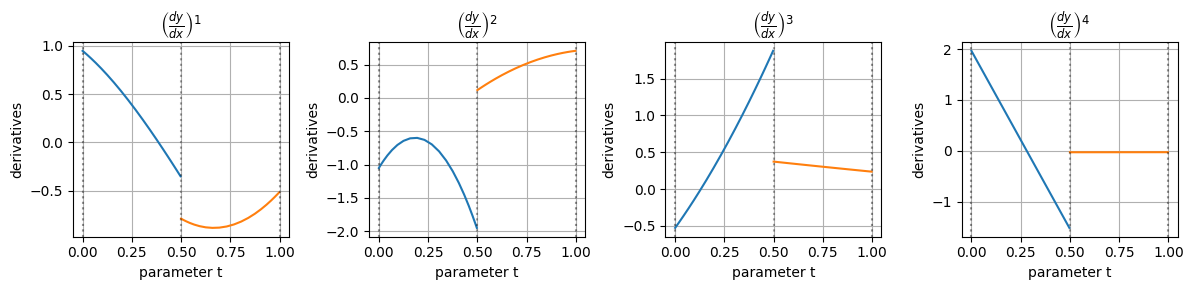
今回は\(k=4\)としたので、\(k-1=3\)階微分までは連続なはずである

BSpline曲線の基底関数を\(k=4\)階微分までグラフにしてみると次のようになる

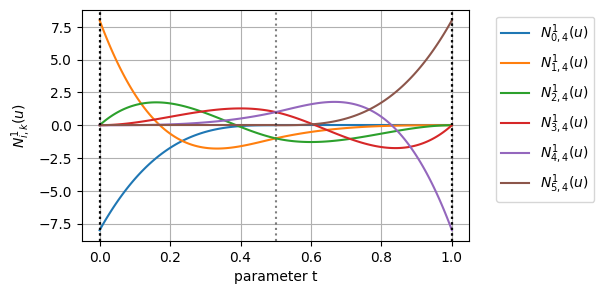
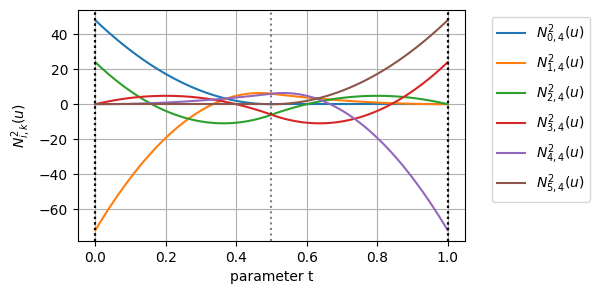
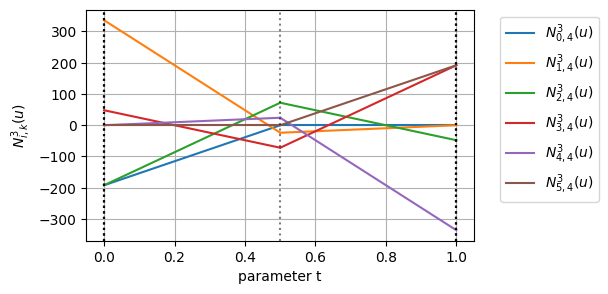
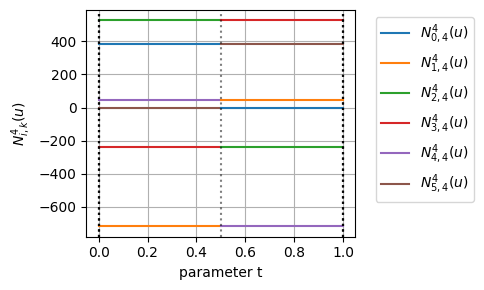
確かに、\(k-1=3\)階微分までの基底関数が連続になっていることが分かる

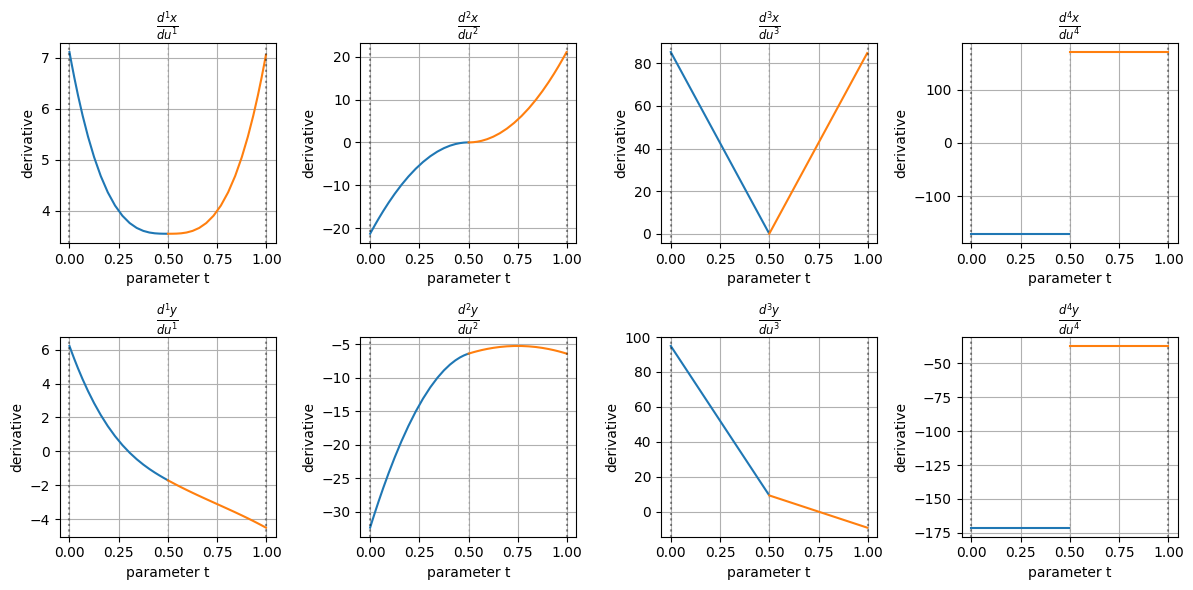
これらの基底関数の微分に制御点をかけるとBSpline曲線の微分\(\frac{d^{r}\mathbf{c}(u)}{du^{r}}=[\frac{d^{r}x}{du^{r}},~\frac{d^{r}y}{du^{r}}] \)が求まる

また、普通に\(y\)を\(x\)で微分すると次のようになる

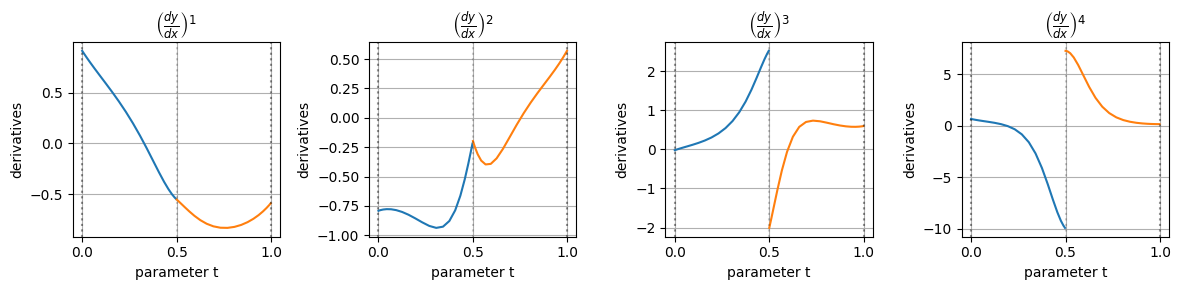
\(k=4\)階微分を見てみると、先ほど説明したセグメントの境界である\(u=0.5\)の位置で４階微分が不連続になっており、ここでもBSpline曲線が２つのセグメントに分かれていることを実感できる

最小制御点数のBSpline曲線

BSpline曲線の制御点の数は、\(k+1\)個以上になるようにしなければならない。

そこで、制御点の数が\(k+1\)個の最小のBSpline曲線を書いてみる

\begin{align}
k &= 4 \\
n &= k + 1 = 5 \\
t &= [0,~ 0,~ 0,~ 0,~ 0,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= n + k + 1 = 10
\end{align}

このBSpline曲線をプロットみると、次のようになる。

制御点の数がk+1のBSpline曲線は、曲線全体が1つのセグメントで構成されていることがわかる。

曲線全体が1つのセグメントで構成されており、すべての制御点が直線全体の形に影響与えるようなBSpline曲線は「ベジェ曲線」と等価になる。

ここまでのポイント

制御点の数が\(k+1\)個のBSpline曲線は曲線全体が1つのセグメントで構成され、すべての制御点が直線全体の形に影響与えるようになる。
このような特殊なBSpline曲線はベジェ曲線と数式的に等価である。

階数k=1のBSpline曲線

BSpline曲線は\(k-1\)階微分まで連続なので、\(k=1\)に設定すると1階微分すら連続でなくなってしまう

実際に\(k=1\)に設定したBSpline曲線を書いてみる

\begin{align}
k &= 1 \\
t &= [0,~ 0,~ 0.25,~ 0.5,~ 0.75,~ 1,~ 1] \\
m &= 7 \\
n &= m - (k + 1) = 7 - 2 = 5
\end{align}

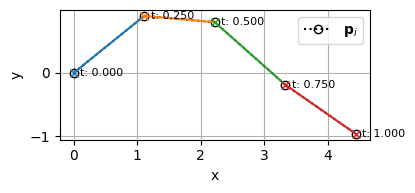
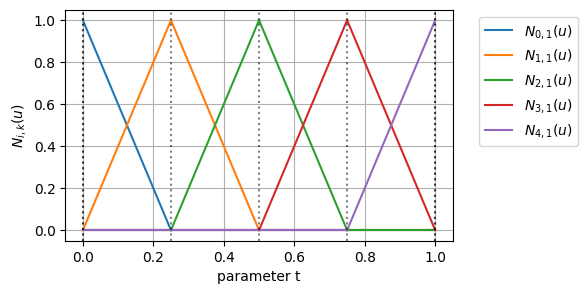
このように、1階微分（傾き）が非連続な曲線、要するに折れ線が完成する。

ここまでのポイント

\(k=1\)に設定したBSpline曲線は折れ線になる。

多重ノットを持つBSpline曲線

BSpline曲線のノットベクトルは単調増加でなければならないが、同じ値を連続させることはできる

ノットベクトルで同じ値を連続させることを多重ノットといい、ノットがいくつ重なっているかを多重度（multiplicity）という

BSpline曲線では、ノットの多重度を1つ上げるごとに、そのパラメーター位置における微分の連続性が1つ下がる

つまり、\(k=4\)の曲線を例にとると

ノットを1つ重ねたパラメーター位置では、3階微分が不連続になる
ノットを2つ重ねたパラメーター位置では、2階微分（曲率）が不連続になる
ノットを3つ重ねたパラメーター位置では、1階微分（傾き）が不連続になる

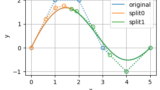
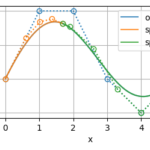
このようなBSpline曲線をプロットすると次のようになる

例①：\(t = 0.5\) で多重度が2の場合

\begin{align}
k &= 4 \\
t &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 12 \\
n &= m - (k + 1) = 12 - 5 = 7
\end{align}

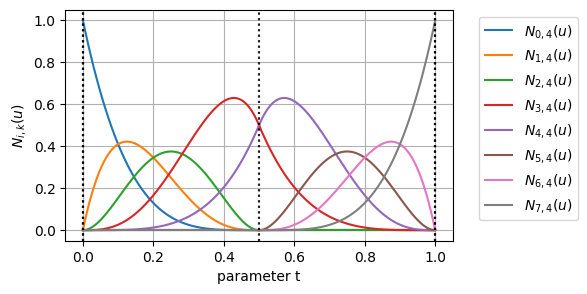
例②：\(t = 0.5\) で多重度が3の場合

\begin{align}
k &= 4 \\
t &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 0.5,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 13 \\
n &= m - (k + 1) = 13 - 5 = 8
\end{align}

例③：\(t = 0.5\) で多重度が4（\(=k\)）の場合

\begin{align}
k &= 4 \\
t &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 0.5,~ 0.5,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 14 \\
n &= m - (k + 1) = 14 - 5 = 9
\end{align}

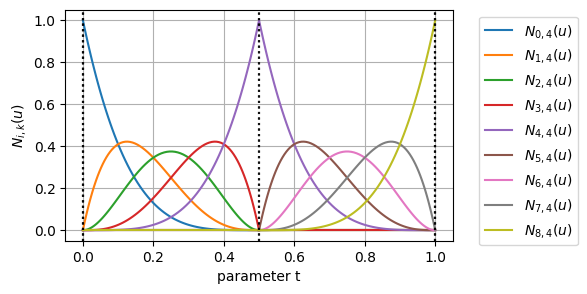
グラフたちを眺めてみると、多重ノットを採用したパラメーター位置において、微分の連続性が徐々に下がっていっていることがわかる

しかも、\(k\)個のノットを重ねた\(t=0.5\)の位置では、基底関数が多重端末ノットを採用したときと同じような値になっており、BSpline曲線が完全に2つに分かれていることがわかる

多重ノットで微分の連続性が下がる理由

de Boor Coxの漸化式のr階微分の式を見てみると分母にノット同士の引き算が出てきている

\begin{align}
N_{i,k}^{r}(t) =\frac{k}{t_{i+k} - t_i} \cdot N_{i,k-1}^{r-1}(t)-\frac{k}{t_{i+k+1} - t_{i+1}} \cdot N_{i+1,k-1}^{r-1}(t)
\end{align}

ノットを連続させて多重ノットにすると、BSpline曲線の基底関数の微分を再帰的に計算する過程で、この分母の部分にゼロ割りが発生し、微分が不連続になってしまう

ちなみに、scipy.interpolate.BSplineでは、ゼロ割を計算できないというエラーが返されてしまう。

ポイント

ノットベクトルの値を連続させると、そのパラメータ位置でのBSpline曲線の微分の連続性が一つ下がる（多重ノット）。
k個のノットを重ねると、BSpline曲線は完全に独立した2つの曲線に分割される

BSpline曲線の階数と次数

あらためて、パラメータ\(u\)におけるBSpline曲線の基底関数\(N_{i,k}(u)\)は、de Boor Coxの漸化式と呼ばれる式で再帰的に定義されている。

\begin{align}
N_{i,k}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,k-1}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(u) \\\\
N_{i,0}(u) &=
\begin{cases}
1 & t_i \leq u < t_{i+1} \\
0 & u < t_i,\quad t_{i+1} \leq u
\end{cases},~ \qquad i=0,~ 1,~ \cdots n-1 \\
\tag{4.1.1}
\end{align}

上記の定式化についてパラメータ\(u\)に対する次数という観点で見ると、例えば\(k=4\)のとき

\begin{align}
N_{i,0}(u) &=
\begin{cases}
1 & t_i \leq u < t_{i+1} \\
0 & u < t_i,\quad t_{i+1} \leq u
\end{cases} \quad
= u\text{の0次式} \\\\
N_{i,~ 1}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,0}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,0}(u) = u\text{の1次式} \\\\
N_{i,~ 2}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,1}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,1}(u) = u\text{の2次式} \\\\
N_{i,~ 3}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,2}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,2}(u) = u\text{の3次式} \\\\
N_{i,~ 4}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,3}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,3}(u) = u\text{の4次式} \\\\
\end{align}

であり、\(k=4\)に対応する基底関数\(N_{i,~ 4}(u)\)は\(u\)の4次式であらわされることがわかる

このことから、4階のBSpline曲線は4次BSpline曲線と呼ばれたりもする

\begin{align}
\mathbf{c}(u) &= \sum_{i=0}^{n-1} N_{i,4}(u) \, \mathbf{p}_i
= u\text{の4次式}
\end{align}