PR

scipy.interpolate.BSplineの使い方

BSpline曲線を作成するためのPythonライブラリであるscipy.interpolate.BSplineと、それに機能を追加した自作クラスであるMyBSplineについて説明する

スポンサーリンク

はじめに

scipy.interpolate.BSplineはBSpline曲線を作成するためのPythonライブラリである

この記事では、scipy.interpolate.BSplineの基本的な使い方と、不足する機能を補った自作クラスMyBSplineについて説明する

↓公式ドキュメント

BSpline — SciPy v1.16.1 Manual
docs.scipy.org

↓関連記事

BSpline曲線の定式化と基本的な性質
BSpline曲線の定式化と基本的な性質について説明する
mtkbirdman.com
2025.08.08

↓参考文献

なお、この記事の数式に付されている式番号は、この参考文献の式番号と対応するようにしている

それではいってみよう

概要

BSpline曲線は以下の式で表される。

\begin{align}
\mathbf{c}(u) = \sum_{i=0}^{n-1} N_{i,k}(u) \, \mathbf{p}_i
\tag{4.2.1}
\end{align}

\begin{align}
\mathbf{c}(u)=\left[\begin{matrix} x_c(u) \\ y_c(u) \\ z_c(u) \end{matrix}\right],
\qquad
\mathbf{p}_i=\left[\begin{matrix} x_{p_i} \\ y_{p_i} \\ z_{p_i} \end{matrix}\right],
\qquad i=0,~ 1,~ \cdots,~ n-1
\end{align}

ここで

  • \(\mathbf{c}(u)\)：BSpline曲線を構成する座標点
  • \(u\)：BSpline曲線の始点から終点までを繋ぐパラメータ
  • \(N_{i,k}(u)\)：BSpline基底関数
  • \(\mathbf{p}_i\)：BSpline曲線の形を決定する\(n\)個の制御点

である

行列形式で表すと、次のようになる

\begin{align}
\begin{bmatrix}
\mathbf{c}(u_0) \\
\mathbf{c}(u_1) \\
\vdots \\
\mathbf{c}(u_{l-1})
\end{bmatrix}
&=
\begin{bmatrix}
N_{0,k}(u_0) & N_{1,k}(u_0) & \cdots & N_{n-1,k}(u_0) \\
N_{0,k}(u_1) & N_{1,k}(u_1) & \cdots & N_{n-1,k}(u_1) \\
\vdots & \vdots & \ddots & \vdots \\
N_{0,k}(u_{l-1}) & N_{1,k}(u_{l-1}) & \cdots & N_{n-1,k}(u_{l-1})
\end{bmatrix}
\begin{bmatrix}
\mathbf{p}_0 \\
\mathbf{p}_1 \\
\vdots \\
\mathbf{p}_{n-1}\end{bmatrix}
\end{align}

ここで、

\begin{align}
\mathbf{C} &=
\begin{bmatrix}
\mathbf{c}(u_0) \\
\mathbf{c}(u_1) \\
\vdots \\
\mathbf{c}(u_{l-1})
\end{bmatrix} \\ \\
\mathbf{N} &=
\begin{bmatrix}
N_{0,k}(u_0) & N_{1,k}(u_0) & \cdots & N_{n-1,k}(u_0) \\
N_{0,k}(u_1) & N_{1,k}(u_1) & \cdots & N_{n-1,k}(u_1) \\
\vdots & \vdots & \ddots & \vdots \\
N_{0,k}(u_{l-1}) & N_{1,k}(u_{l-1}) & \cdots & N_{n-1,k}(u_{l-1})
\end{bmatrix} \\ \\
\mathbf{P} &=
\begin{bmatrix}
\mathbf{p}_0 \\
\mathbf{p}_1 \\
\vdots \\
\mathbf{p}_{n-1}\end{bmatrix}
\end{align}

とすると

\begin{align}
\mathbf{C} &= \mathbf{N}\, \mathbf{P}
\end{align}

となる。この記事では\(\mathbf{N}\)を基底関数行列と呼ぶことにする（一般的にどう呼ばれているかは知らない）

パラメータ\(u\)におけるBSpline曲線の基底関数\(N_{i,k}(u)\)は、de Boor Coxの漸化式と呼ばれる式で再帰的に定義される。

\begin{align}
N_{i,k}(u) &= \frac{u - t_i}{t_{i+k-1} - t_i} N_{i,k-1}(u) + \frac{t_{i+k} - u}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(u) \\\\
N_{i,1}(u) &=
\begin{cases}
1 & t_i \leq u < t_{i+1} \\
0 & \text{otherwise}
\end{cases},~ \qquad i=0,~ 1,~ \cdots n-1 \\
\tag{4.1.1}
\end{align}

ここで、ノットベクトル\(\mathbf{t}\)の長さ\(m\)および制御点\(\mathbf{p}_{i}\)の数\(n\)は以下の条件を満たしていなければならない

\begin{align}
m &= n+(k+1) \\\\
n &\geq k+1
\end{align}

ノットベクトル、制御点、階数について、scipy.interpolate.BSplineでは以下の変数名が用いられている

  • t：ノットベクトル\(\mathbf{t}\)（knot vector）
  • c：制御点\(\mathbf{p}_{i}\)（spline coefficients）
  • k：階数\(k\)（spline degree）

機能

scipy.interpolate.BSplineの機能をまとめると以下の通り

できること
  • t, c, kを用いたBSpline曲線の定義
  • BSpline曲線の取得
  • 基底関数行列の取得
  • 微分の計算
  • ノット挿入
できないこと
  • 階数上げ
  • 曲率の計算

「できないこと」については、この記事の後半においてscipy.interpolate.BSplineを継承した自作クラスのメソッドとして実装を行う

というわけでまずは、「できること」について説明していく

BSpline曲線の定義

以下のBSpline曲線を考える

\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}

scipy.interpolate.BSplineでは、BSpline(t, c, k)でBSpline曲線を定義できる

import numpy as np
from scipy.interpolate import BSpline

# set parameter (t, c, k)
k = 4
t = np.array([0, 0, 0, 0, 0, 0.5, 1, 1, 1, 1, 1], dtype=float)
c = np.array([
    [0.0, 0.0],   # c0
    [0.5, 1.2],   # c1
    [1.5, 0.4],   # c2
    [2.0, 2.2],   # c3
    [3.0, -0.6],  # c4
    [4.0, 0.0],   # c5
], dtype=float)

# define bspline curve
bspline = BSpline(t, c, k)

返値のbsplineはBSplineクラスのオブジェクトになる

定義したBSpline曲線のノットベクトル、制御点、階数はそれぞれbspline.t、bspline.c、bspline.k、もしくはbspline.tckで取得できる

print('t:', bspline.t)
print('c:', bspline.c)
print('k:', bspline.k)
t, c, k = bspline.tck
print('t:', t)
print('c:', c)
print('k:', k)
t: [0.  0.  0.  0.  0.  0.5 1.  1.  1.  1.  1. ]
c: [[ 0.   0. ]
 [ 0.5  1.2]
 [ 1.5  0.4]
 [ 2.   2.2]
 [ 3.  -0.6]
 [ 4.   0. ]]
k: 4
よくあるエラー

ノットベクトルの長さが\(m=n+(k+1)\)を満たしていないと、次のエラーが出る

ValueError: Knots, coefficients and degree are inconsistent.

BSpline曲線の取得

BSpline曲線の座標はBSplineクラスのオブジェクトに引数としてパラメータuを与えることでndarrayとして取得できる（__call__）

# evaluate
u_min = np.min(bspline.t)
u_max = np.max(bspline.t)
u = np.linspace(u_min, u_max, 101)
curve = bspline(u)

# plot
import matplotlib.pyplot as plt
import matplotlib.cm as cm

fig, ax = plt.subplots(figsize=(4, 3))
ax.plot(c[:, 0], c[:, 1], 'o:', markerfacecolor='none', color='k', label='$\mathbf{p}_{i}$')
ax.plot(curve[:, 0], curve[:, 1], label='$\mathbf{c}(u)$')
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal')
ax.grid(True)
plt.tight_layout()
plt.show()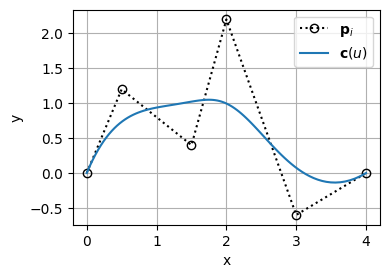

返ってくるndarrayの大きさは、与えたuの大きさと同じになる

print('u.shape:\t', u.shape)
print('curve.shape:\t', curve.shape)
u.shape:	 (101,)
curve.shape:	 (101, 2)

基底関数行列の取得

scipy.interpolate.BSplineを使って基底関数行列を取得する方法は3つある

  1. design_matrix()を使う方法
  2. basis_element()を使う方法
  3. cに単位行列を与える方法

もちろんどれも同じ結果が得られるが、いちおう「1. design_matrix()を使う方法」が公式が用意したデフォルトの方法なので、一番効率がいいと思われる

以下のBSpline曲線を例として、1つずつ説明していく

\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}

import numpy as np
from scipy.interpolate import BSpline
np.set_printoptions(formatter={'float': '{:8.3f}'.format}, linewidth=999)

k = 4
t = np.array([0, 0, 0, 0, 0, 0.5, 1, 1, 1, 1, 1], dtype=float)
l = 5
x = np.linspace(0, 1, l)
m = len(t)
n = m - (k + 1)

print('t:', t)
print('x:', x)
print('k:', k, '\tl:', l, '\tm:', m, '\tn:', n)
t: [   0.000    0.000    0.000    0.000    0.000    0.500    1.000    1.000    1.000    1.000    1.000]
x: [   0.000    0.250    0.500    0.750    1.000]
k: 4 	l: 5 	m: 11 	n: 6

BSpline.design_matrix(x, t, k, extrapolate=False)

パラメータ\(u\)、ノットベクトル\(\mathbf{t}\)、階数\(k\)を引数として、基底関数行列\(\mathbf{N}\)のCSR形式の疎行列オブジェクトを返してくれるメソッド

CSR形式の疎行列オブジェクトは簡単にndarrayに変換できる

引数

  • x : array_like, shape (n,)(n,)
    BSpline曲線の基底関数行列を取得するパラメータ\(u\)の配列。
  • t : array_like, shape (nt,)(n_t,)
    ノットベクトル
  • k : int
    BSpline曲線の階数（degree）。
  • extrapolate : bool または 'periodic', オプション（デフォルト：False）
    最初と最後の区間に基づいて外挿するか（True）、エラーを出すか（False）、または周期外挿 ('periodic') を使うかを指定する

戻り値

CSR形式は疎行列を効率よく表すための形式で、toarray()メソッドを使えばndarrayに変換できる

使用例

basis_matrix = BSpline.design_matrix(u, t, k).toarray()

print(basis_matrix)
[[   1.000    0.000    0.000    0.000    0.000    0.000]
 [   0.062    0.508    0.336    0.086    0.008    0.000]
 [   0.000    0.125    0.375    0.375    0.125    0.000]
 [   0.000    0.008    0.086    0.336    0.508    0.062]
 [   0.000    0.000    0.000    0.000    0.000    1.000]]

basis_matrixは\(l\)行\(n\)列の2次元配列になる

print('basis_matrix.shape: ', basis_matrix.shape)
print(f'(l, n) = ({l}, {n})')
basis_matrix.shape:  (5, 6)
(l, n) = (5, 6)

BSpline.basis_element(t, extrapolate=True)

ノットベクトルの部分区間（長さ\(k+2\)）を与えると、それに対応する基底関数のBSplineオブジェクトを返してくれるメソッド

ちょっと使い方が難しい

引数

  • t : array_like, shape (k+2,)
    ノットベクトルの部分区間（長さは\(k+2\)）
  • extrapolate : bool, optional, 既定値は True
    基底関数の定義域外で評価したときに外挿を行うかどうかを指定する
    False に設定すると、定義域外では NaN が返される

戻り値

  • bspline : BSpline オブジェクト
    与えられたノットベクトルの部分区間tによって定義される基底関数
    Bsplineオブジェクトなので、パラメータを引数として呼び出せる（bspline(x)）

使用例

basis_matrix = np.zeros((len(x), n))

x[-1] -= (1e-10)
for i in range(n):
    t_internal = t[i:i + k + 2]
    basis_func = BSpline.basis_element(t_internal, extrapolate=False)
    basis_matrix[:, i] = basis_func(x)

print(basis_matrix)
[[   1.000    0.000    0.000    0.000    0.000      nan]
 [   0.062    0.508    0.336    0.086    0.008      nan]
 [   0.000    0.125    0.375    0.375    0.125    0.000]
 [     nan    0.008    0.086    0.336    0.508    0.062]
 [     nan    0.000    0.000    0.000    0.000    1.000]]

制御点ごとにfor i in range(n):のループを回す必要があり、ノットベクトルの部分区間の定義域の外ではnanが挿入される

また、定義域の境界（\(u=0,~ 1\)）では丸め誤差の影響でうまく計算できないことがあるので、x[-1] -= (1e-10)として丸め誤差の影響を打ち消している（めんどくさい）

cに単位行列を与える方法

ちょっとひねったやり方

この記事の最初で示した通り、BSpline曲線を行列形式で表すと次のようになる

\begin{align}
\mathbf{C} &= \mathbf{N}\, \mathbf{P}
\end{align}

ここから分かる通り、BSpline曲線の制御点群\(\mathbf{P}\)（scipy.interpolate.BSplineではより一般的に「BSpline曲線の係数」と呼ばれている）に単位行列\(\mathbf{I}\)を与えると、出力される座標点群\(\mathbf{C}\)は基底関数行列\(\mathbf{N}\)になる

\begin{align}
\mathbf{C} &= \mathbf{N}\, \mathbf{I} = \mathbf{N}
\end{align}

このとき、それぞれの行列の大きさは

\begin{align}
(l,~ n) &= (l,~ n) \times (n,~ n)
\end{align}

である

使用例

c = np.eye(n, n)
bspline = BSpline(t, c, k)
basis_matrix = bspline(x)

print(basis_matrix)
[[   1.000    0.000    0.000    0.000    0.000    0.000]
 [   0.062    0.508    0.336    0.086    0.008    0.000]
 [   0.000    0.125    0.375    0.375    0.125    0.000]
 [   0.000    0.008    0.086    0.336    0.508    0.062]
 [   0.000    0.000    0.000    0.000    0.000    1.000]]

同じ結果が得られていることが分かる

微分の取得

scipy.interpolate.BSplineを使ってBSpline曲線のr階微分を取得する方法は2つある

  1. derivative()を使う方法
  2. __call__()を使う方法

もちろんどれも同じ結果が得られるが、「1. derivative()を使う方法」では多重ノットなどで微分が不連続になったときにエラーが出てしまうので、2.の方法の方がいい気がする

以下のBSpline曲線を例として、1つずつ説明していく

\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 0.5,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 13 \\
n &= m - (k + 1) = 13 - 5 = 8 \\
\end{align}

import numpy as np
from scipy.interpolate import BSpline

# set parameter (t, c, k)
k = 4
t = np.array([0, 0, 0, 0, 0, 0.5, 0.5, 0.5, 1, 1, 1, 1, 1], dtype=float)
c = np.array([
    [0.0, 0.0],   # c0
    [0.5, 1.2],   # c1
    [1.0, 2.5],   # c2
    [1.5, 0.4],   # c3
    [2.0, 2.2],   # c4
    [2.5, 1.8],   # c5
    [3.0, -0.6],  # c6
    [4.0, 0.0],   # c7
], dtype=float)
l = 101
u = np.linspace(np.min(t), np.max(t), l)
m = len(t)
n = m - (k + 1)

print('t:', t)
print('k:', k, '\tl:', l, '\tm:', m, '\tn:', n)
t: [   0.000    0.000    0.000    0.000    0.000    0.500    0.500    0.500    1.000    1.000    1.000    1.000    1.000]
k: 4 	l: 101 	m: 13 	n: 8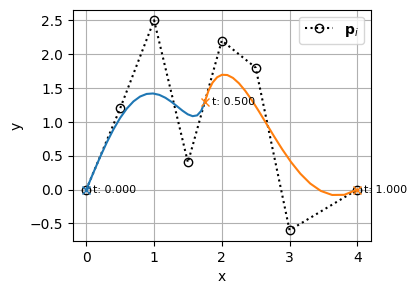

BSpline.derivative(nu=1)

BSpline曲線のr階微分の導関数を表す新しいBSplineオブジェクトを返してくれる

引数

  • nu : int, 任意（省略時：1）
    求めたい導関数の階数。デフォルトでは1階（一次導関数）

戻り値

  • b : BSpline オブジェクト
    元のスプラインの nu 階導関数を表す BSplineオブジェクト

使用例

r=1
bspline = BSpline(t, c, k)
bspline_deriv = bspline.derivative(nu=r)
deriv = bspline_deriv(u)
print(deriv)
[[   4.000    9.600]
 [   4.000    9.615]
 [   4.000    9.567]
 ...
 [   7.539    2.109]
 [   7.765    3.408]
 [   8.000    4.800]]
# plot
import matplotlib.pyplot as plt
import matplotlib.cm as cm

fig, axes = plt.subplots(figsize=(3 * k, 3 * 2), ncols=k, nrows=2, squeeze=False)
axis_label = ['x', 'y', 'z']

bspline = BSpline(t, c, k)
for i in range(2):
    for r in range(1, k + 1):
        ax = axes[i, r - 1]
        t_unique = np.array(sorted(set(t.tolist())))
        for j, (t0, t1) in enumerate(zip(t_unique[:-1], t_unique[1:])):
            try:
                bspline_deriv = bspline.derivative(nu=r)
                u = t0 + 0.5 * (1 - np.cos(np.pi * np.linspace(0, 1, 22)[:-1])) * (t1 - t0)
                deriv = bspline_deriv(u)
                ax.plot(u, deriv[:, i], color=cm.tab10(j % 10))
            except:
                print(f'ValueError: The spline has internal repeated knots and is not differentiable {r} times')
                pass

        for knot in t:
            ax.axvline(knot, linestyle=':', color='k', alpha=0.1)
        
        ax.set_xlabel('$u$')
        ax.set_ylabel('derivative')
        ax.set_title(rf'$\frac{{d^{r}{axis_label[i]}}}{{du^{{{r}}}}}$')
        ax.grid(True)

plt.tight_layout()
plt.show()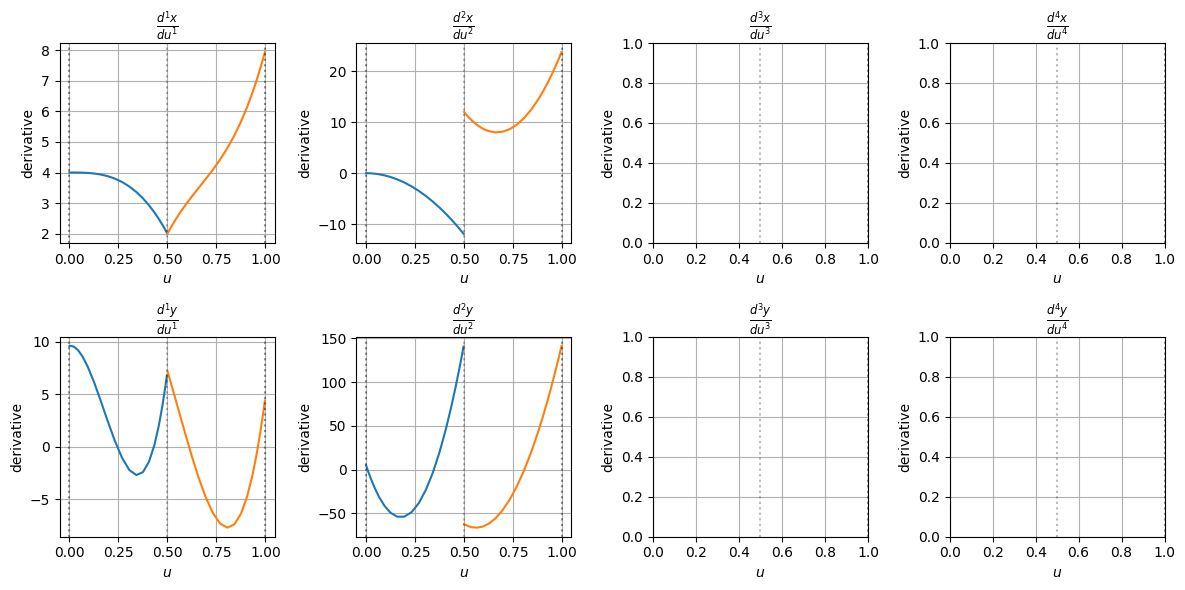

今回は\(t=0.5\)における多重度が3なので、1階微分まで連続、2階微分は不連続、それゆえ3階微分以降は計算できていない

よくあるエラー

多重ノットなどで微分が不連続になっているときはエラーが出る

ValueError: The spline has internal repeated knots and is not differentiable 3 times

BSpline.__call__(x, nu=0, extrapolate=None)

この記事の最初のほうでBSpline曲線の座標を取得するのに使ったが、なんと引数nuを使えば微分を取得することもできる

しかも、ドキュメントには明記されていないが、多重ノットを使用して微分が不連続になっている階数も、区分的に微分を行うことでいい感じに計算してくれる

引数

  • x : array_like
    BSpline曲線のパラメータ
  • nu : int, オプション（デフォルト：0）
    導関数の階数。nu=0 のときは関数値そのものが返ってくる。
  • extrapolate : bool または 'periodic', オプション（デフォルト：self.extrapolate）
    定義域外の値に対して外挿するか、NaN を返すか、を制御する。
    • True の場合：最初／最後のスプライン区間に基づいて外挿
    • False の場合：定義域外では NaN
    • 'periodic' の場合：周期外挿

戻り値

  • y : array_like
    BSpline曲線あるいはその微分

使用例

r=1
bspline = BSpline(t, c, k)
deriv = bspline(u, nu=r)
print(deriv)
[[   4.000    9.600]
 [   4.000    9.615]
 [   4.000    9.567]
 ...
 [   7.539    2.109]
 [   7.765    3.408]
 [   8.000    4.800]]
# plot
import matplotlib.pyplot as plt
import matplotlib.cm as cm

fig, axes = plt.subplots(figsize=(3 * k, 3 * 2), ncols=k, nrows=2, squeeze=False)
axis_label = ['x', 'y', 'z']

for i in range(2):
    for r in range(1, k + 1):
        ax = axes[i, r - 1]
        t_unique = np.array(sorted(set(t.tolist())))
        
        for j, (t0, t1) in enumerate(zip(t_unique[:-1], t_unique[1:])):
            u = t0 + 0.5 * (1 - np.cos(np.pi * np.linspace(0, 1, 22)[:-1])) * (t1 - t0)
            deriv = bspline(u, nu=r)
            ax.plot(u, deriv[:, i], color=cm.tab10(j % 10))

        for knot in t:
            ax.axvline(knot, linestyle=':', color='k', alpha=0.1)
        
        ax.set_xlabel('$u$')
        ax.set_ylabel('derivative')
        ax.set_title(rf'$\frac{{d^{r}{axis_label[i]}}}{{du^{{{r}}}}}$')
        ax.grid(True)

plt.tight_layout()
plt.show()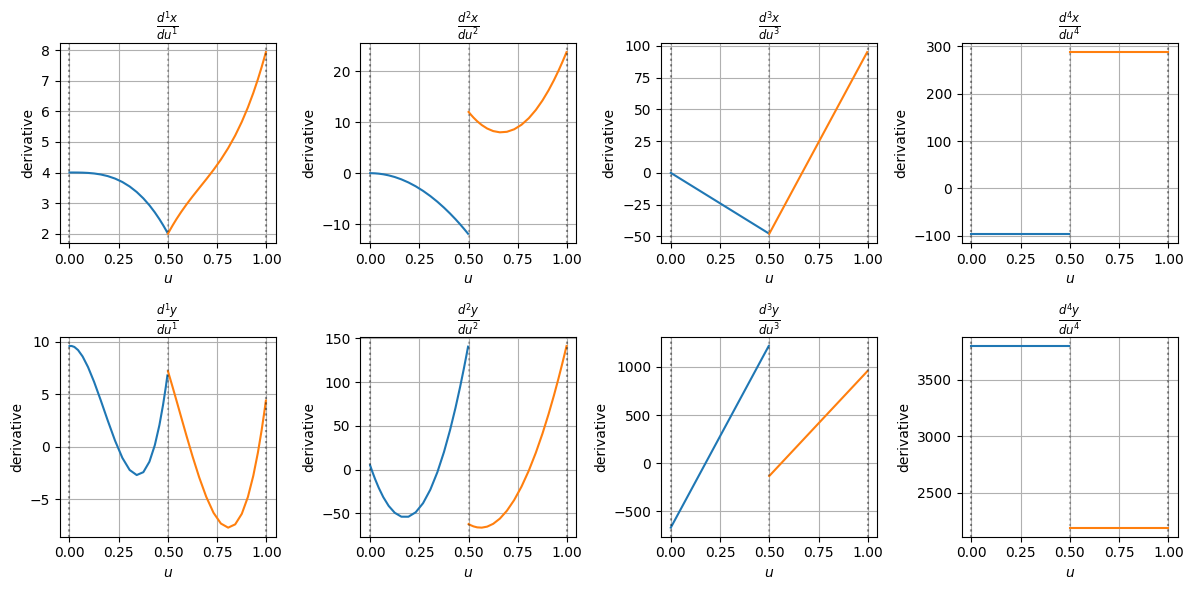

このように、微分が不連続になっている階数以降の微分も計算してくれていることがわかる

ノットの挿入

ノットの挿入はinsert_knotメソッドが用意されている

以下のBSpline曲線を例として説明する

\begin{align}
k &= 4 \\
\mathbf{t} &= [0,~ 0,~ 0,~ 0,~ 0,~ 0.5,~ 1,~ 1,~ 1,~ 1,~ 1] \\
m &= 11 \\
n &= m - (k + 1) = 11 - 5 = 6 \\
\end{align}

import numpy as np
from scipy.interpolate import BSpline

# set parameter (t, c, k)
k = 4
t = np.array([0, 0, 0, 0, 0, 0.5, 1, 1, 1, 1, 1], dtype=float)
c = np.array([
    [0.0, 0.0],   # c0
    [0.5, 1.2],   # c1
    [1.5, 0.4],   # c2
    [2.0, 2.2],   # c3
    [3.0, -0.6],  # c4
    [4.0, 0.0],   # c5
], dtype=float)

# define bspline curve
bspline = BSpline(t, c, k)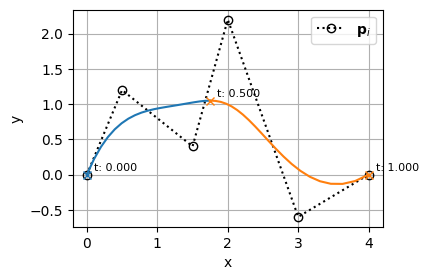

BSpline.insert_knot(x, m=1)

指定した位置にノットを挿入した新しいBsplineオブジェクトを返してくれるメソッド。

引数

  • x : float
    新たに挿入するノットの位置。
  • m : int, オプション（デフォルト：1）
    指定した位置 x に挿入する回数（ノットの多重度）。

戻り値

  • BSpline オブジェクト
    新しいノットが追加されたノットベクトル t、それに対応する係数 c、および同じ次数 k を持つ、新しい BSplineオブジェクトを返す

使用例①

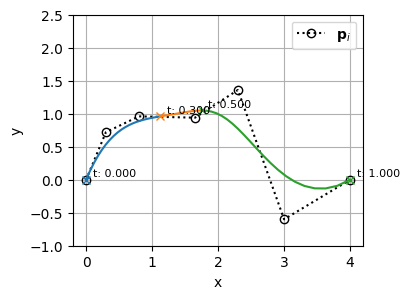
\(t=0.3\)の位置にノットを1つ追加する

bspline0 = bspline.insert_knot(x=0.3, m=1)

print('t:', bspline0.t)
plot_bspline(bspline0)
plot_basis_matrix(bspline0)
t: [0.00 0.00 0.00 0.00 0.00 0.30 0.50 1.00 1.00 1.00 1.00 1.00]
def plot_bspline(bspline, ref_points=None, show=False, legend=True, figsize=(4, 3), seg=True):
    t = bspline.t
    c = bspline.c
    k = bspline.k

    fig, ax = plt.subplots(figsize=figsize)

    # 制御点を点線でプロット
    ax.plot(c[:, 0], c[:, 1], 'o:', markerfacecolor='none', color='k', label='$\mathbf{p}_{i}$')

    if seg:
        # 重複を除いたノット値のリスト
        t_unique = np.array(sorted(set(t.tolist())))

        # 各ノット区間ごとに曲線を描画
        for i, (t0, t1) in enumerate(zip(t_unique[:-1], t_unique[1:])):
            color = cm.tab10(i % 10)  # 10色のカラーマップをループ使用
            u = np.linspace(t0, t1, 21)
            curve = bspline(u)  # 曲線上の点群

            ax.plot(curve[:, 0], curve[:, 1], color=color)

            # 区間端点の描画とラベル
            point_start = bspline(t0)
            ax.plot(point_start[0], point_start[1], 'x', color=color)
            ax.text(point_start[0] + 0.1, point_start[1] + 0.1, f't: {t0:.3f}', fontsize=8, color='k', ha='left', va='center')
        point_end = bspline(t1)
        ax.plot(point_end[0], point_end[1], 'x', color=color)

        ax.text(point_end[0] + 0.1, point_end[1] + 0.1, f't: {t1:.3f}', fontsize=8, color='k', ha='left', va='center')
    else:
        t0, t1 = np.min(t), np.max(t)
        u = np.linspace(t0, t1, 101)
        curve = bspline(u)  # 曲線上の点群

        ax.plot(curve[:, 0], curve[:, 1], label='$\mathbf{c}(u)$')

    # 参照点がある場合は描画
    if ref_points is not None:
        ref_points = np.asarray(ref_points)
        ax.plot(ref_points[:, 0], ref_points[:, 1], 'o', label='reference points')

    if legend:
        ax.legend()

    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_aspect('equal')
    ax.grid(True)

    if show:
        plt.show()


def plot_basis_matrix(bspline):

  t, c, k = bspline.tck
  c_eye = np.eye(len(c), len(c))
  bspline = BSpline(t, c_eye, k)

  axis_label = ['x', 'y', 'z']

  for r in range(0, k + 1):
      fig, ax = plt.subplots(figsize=(4, 3))
      t_unique = np.array(sorted(set(t.tolist())))

      for j, (t0, t1) in enumerate(zip(t_unique[:-1], t_unique[1:])):
          u = t0 + 0.5 * (1 - np.cos(np.pi * np.linspace(0, 1, 22)[:-1])) * (t1 - t0)
          deriv = bspline(u, nu=r)
          ax.plot(u, deriv) #, color=cm.tab10(j % 10))

      for knot in t:
          ax.axvline(knot, linestyle=':', color='k', alpha=0.1)

      ax.set_xlabel('$u$')
      ax.set_ylabel('$N_{{i,k}}$')
      ax.grid(True)

  plt.tight_layout()
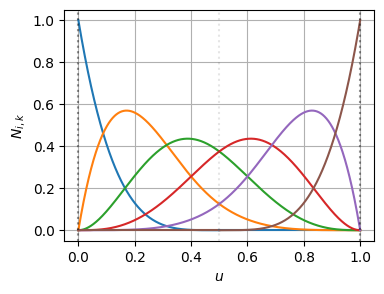
  plt.show()

ノットを挿入したことで基底関数の形状は変わっている

ノット挿入前
ノット挿入後

が、BSpline曲線の形状が変化しないように制御点の位置を計算している

ノット挿入前
ノット挿入後

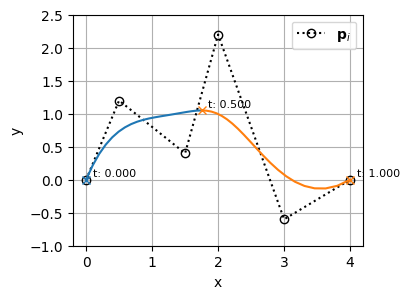
使用例②

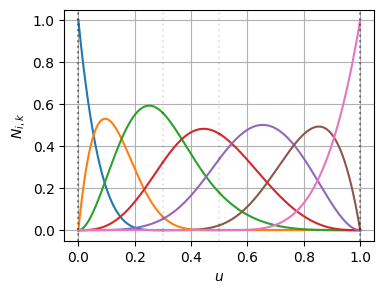
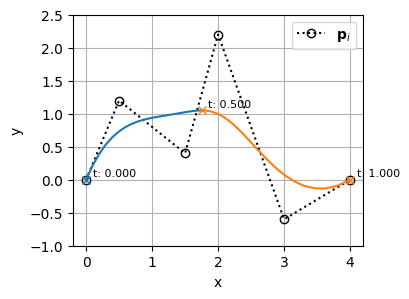
\(t=0.5\)の位置にノットを3つ追加する（t=0.5でノットを4つ重ねる）

bspline1 = bspline.insert_knot(x=0.5, m=3)

print('t:', bspline1.t)
plot_bspline(bspline1)
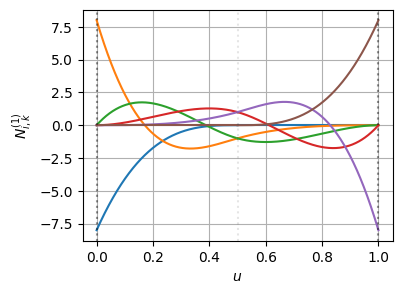
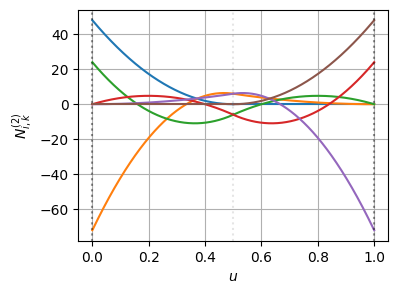
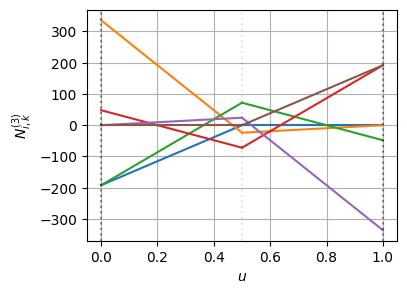
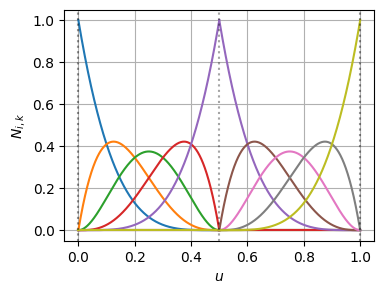
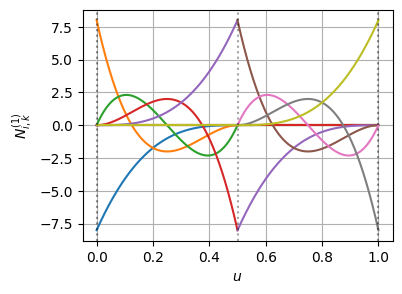
plot_basis_matrix(bspline1)
t: [0.00 0.00 0.00 0.00 0.00 0.50 0.50 0.50 0.50 1.00 1.00 1.00 1.00 1.00]

こちらもノットの挿入前後でBSpline曲線の形状は変わっていない（=微分の連続性も保たれている）

ノット挿入前
ノット挿入後

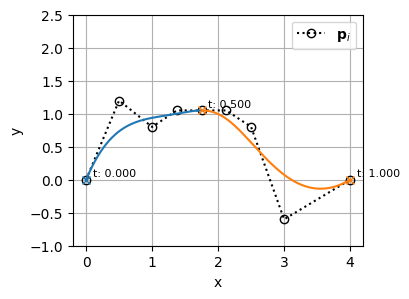
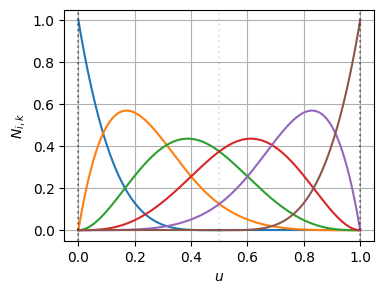
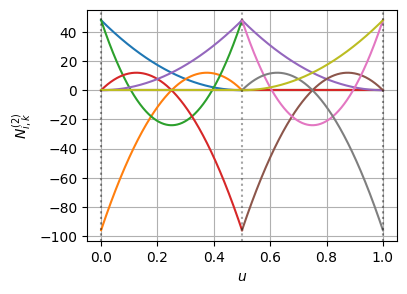
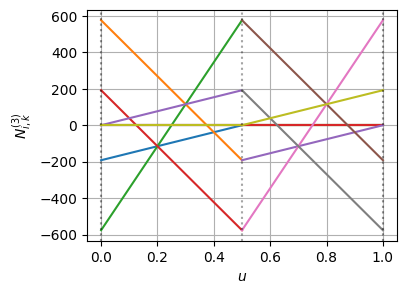
基底関数とその微分はこんな感じになっている

ノット挿入前（\(r=0\)）
ノット挿入前（\(r=1\)）
ノット挿入前（\(r=2\)）
ノット挿入前（\(r=3\)）

ノット挿入後（\(r=0\)）
ノット挿入後（\(r=1\)）
ノット挿入後（\(r=2\)）
ノット挿入後（\(r=3\)）

自作クラスの定義

冒頭で説明した通り、scipy.interpolate.BSplineではいくつか実装されていない機能があるので、BSplineクラスを継承した自作クラスMyBSplineクラスを作り、必要な機能を実装する

from scipy.interpolate import BSpline

class MyBSpline(BSpline):

    def __init__(self, t=None, c=None, k=4):
        
        # BSpline の初期化
        if t is not None and c is not None:
            super().__init__(t, c, k)

    # ここから自作メソッドを定義

MyBSplineクラスはBSplineクラスを継承しているので、これまで紹介したメソッドはそのまま使うことができる

階数上げ

↓長くなったので別記事にまとめた

scipy.interpolate.BSplineで次数上げを実装する
scipy.interpolate.BSplineにデフォルトで実装されていない次数上げ（degree elevation）の機能を補った自作クラスMyBSplineの作る
mtkbirdman.com
2025.08.12

曲率の計算

BSpline曲線（より一般的にはパラメータ\(t\)であらわされる曲線\(\mathbf{r}(t)\)）の曲率は以下の式で計算できる

\begin{align}
\kappa(t) &= \frac{\lVert \mathbf{r}'(t) \times \mathbf{r}''(t) \rVert}{\lVert \mathbf{r}'(t) \rVert^{3}} \quad \text{(3D)} \
\kappa(t) &= \frac{\left| x'(t)\,y''(t) - y'(t)\,x''(t) \right|}{\left( x'(t)^{2} + y'(t)^{2} \right)^{3/2}} \quad \text{(2D)}
\end{align}

これを自作クラスであるMyBSplineクラスにcurvatureメソッドとして実装する

MyBSpline.curvature(self, x)

BSpline曲線の指定したパラメータ位置での曲率 κ(t) を計算するメソッド

def curvature(self, x):
    """
    Bスプライン曲線における、指定したパラメータ位置での曲率 κ(t) を計算する。
    2次元および3次元に対応し、入力はスカラーまたは配列のいずれでも可。

    パラメータ
    ----------
    x : float または array_like
        曲率を評価するパラメータ値（スカラーまたは配列）

    戻り値
    -------
    float または ndarray
        指定したパラメータ位置での曲率値。
        3次元曲線の場合: κ(t) = ||r'(t) × r''(t)|| / ||r'(t)||³
        2次元曲線の場合: κ(t) = |x'(t) y''(t) - y'(t) x''(t)| / (x'(t)² + y'(t)²)^(3/2)
    """

    # 1階微分ベクトル：パラメータxにおける接ベクトル r'(t)
    r1 = self(x, nu=1)
    # 2階微分ベクトル：パラメータxにおける接ベクトルの変化 r''(t)
    r2 = self(x, nu=2)

    # 配列の形を統一（(N, dim)）スカラーなら (1, dim) に変換
    r1 = np.atleast_2d(r1)
    r2 = np.atleast_2d(r2)

    dim = r1.shape[1]  # 次元数

    if dim == 3:
        # 3D: 外積の大きさを計算
        cross_norm = np.linalg.norm(np.cross(r1, r2), axis=1)
    elif dim == 2:
        # 2D: 外積の z 成分（スカラー外積）を計算
        cross_norm = np.abs(r1[:, 0] * r2[:, 1] - r1[:, 1] * r2[:, 0])
    else:
        raise ValueError("This function supports only 2D or 3D curves.")

    # ||r'(t)|| の計算
    r1_norm = np.linalg.norm(r1, axis=1)

    # ゼロ除算を避けるため、非常に小さい値を置き換え
    eps = np.finfo(float).eps
    safe_r1_norm = np.maximum(r1_norm, eps)

    # 曲率公式の適用
    kappa = cross_norm / (safe_r1_norm ** 3)

    # 入力がスカラーならスカラーで返す
    if np.isscalar(x):
        return float(kappa[0])
    return kappa

引数

  • x : float または array_like
    曲率を評価するパラメータ値

戻り値

  • float または ndarray
    指定したパラメータ位置での曲率値

使用例

# set parameter (t, c, k)
k = 4
t = np.array([0, 0, 0, 0, 0, 0.5, 1, 1, 1, 1, 1], dtype=float)
c = np.array([
    [0.0, 0.0],   # c0
    [0.5, 1.2],   # c1
    [1.5, 0.4],   # c2
    [2.0, 2.2],   # c3
    [3.0, -0.6],  # c4
    [4.0, 0.0],   # c5
], dtype=float)

# define bspline curve
bspline = MyBSpline(t, c, k)
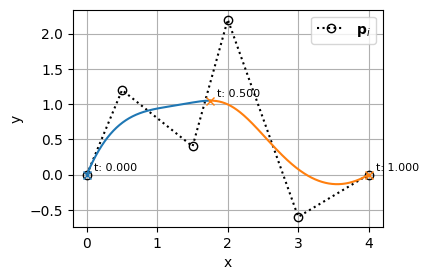
plot_bspline(bspline)

# calculate curvature
u = np.linspace(0, 1, 999)
curvature = bspline.curvature(u)

# plot
import matplotlib.pyplot as plt
import matplotlib.cm as cm

fig, ax = plt.subplots(figsize=(4, 3))
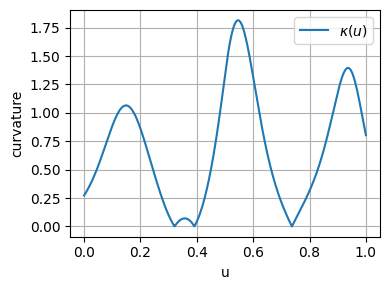
ax.plot(u, curvature, label='$\kappa(u)$')
ax.legend()
ax.set_xlabel('u')
ax.set_ylabel('curvature')
ax.grid(True)
plt.tight_layout()
plt.show()

結果はこんな感じ

おわりに

BSpline曲線を作成するためのPythonライブラリであるscipy.interpolate.BSplineと、それに機能を追加した自作クラスであるMyBSplineについて説明した

↓関連記事

【まとめ】BSpline曲線入門
BSpline曲線について解説した記事のまとめ
mtkbirdman.com
2025.08.08
NURBS
python
質問・感想・意見などあれば気軽にTwitterのDMかコメントお願いします！
スポンサーリンク
@mtk_birdman
スポンサーリンク

コメント