滑空機に搭載されている計器である高度計、速度計、トータルエナジー・バリオメーターについて説明する
はじめに
滑空機には、高度計、速度計、トータルエナジー・バリオメーターなどのアナログ計器が搭載されている
| 入力元 | 入力 | 出力 | 出力先(計器) |
|---|---|---|---|
| 静圧孔 | 静圧 | 高度 | 高度計 (ALT:Altimeter) |
| 静圧孔 ピトー管 | 静圧 全圧 | IAS (指示対気速度) | 速度計 (ASI:Airspeed indicator) |
| 静圧孔 | 静圧 | 鉛直速度 | 非補償式バリオメーター (Uncompensated Variometer) |
| TEプローブ | 静圧-動圧 | エネルギー高度の 時間変化率 | TE補償式バリオメーター (Total Energy Variometer) |
いずれも「圧力」をもとにしている計器である
この記事では、これらの計器について、定式化も含めて説明する
滑空機に搭載されている計器はアナログ式のものが多いため、いくつかの物理法則を理解しておく必要がある
ベルヌーイの定理
みんな大好きベルヌーイの定理
理想流体(粘性のない非圧縮性の流体)において、流れに沿って全圧=静圧+動圧が一定となるという定理である
\begin{align}
p_t
& = p_a + \frac{1}{2}\rho V_{\infty}^2 \\\\
& = p_s + \frac{1}{2}\rho V^2 \\\\
& = \text{const.}
\end{align}
- \(p_t\):全圧 [Pa] = [N/m2]
- \(p_a\):大気圧 [Pa]
- \(V_{\infty}\):一様流速(対気速度) [m/s]
- \(p_s\):ある点での静圧 [Pa]
- \(V\):ある点での速度 [m/s]
- \(\rho\):空気密度 [kg/m3]
機体が静止しているとき
まず、1番簡単な機体が静止しているときを考えると、速度はゼロ(\(V=0\))なので、全圧=静圧となり、このときの圧力は大気圧と同じになる
\begin{align}
p_t=p_s=p_a
\end{align}
機体が対気速度\(V_{\infty}\)で飛行しているとき
機体が対気速度\(V_{\infty}\)で飛行すると、一様流の全圧\(p_t\)が一様流速の2乗に比例した分だけ大きくなる
\begin{align}
p_t=p_a+\frac{1}{2}\rho {V_{\infty}}^2
\end{align}
ここで増加した速度の2乗に比例する圧力成分を動圧\(q\)(\(=\frac{1}{2}\rho V^2\))という
また、機体周りの流れの速度は一定ではなく、ある場所では減速され、ある場所では加速されている
このとき、機体表面上のある点での静圧を\(p_s\)、速度を\(V\) とすると、この点での全圧は一様流の全圧と等しくなる
\begin{align}
p_t &= p_a+\frac{1}{2}\rho {V_{\infty}}^2 \\\\
&= p_s+\frac{1}{2}\rho V^2
\end{align}
これがベルヌーイの定理である
例えば、\(V=0\)となる点(淀み点)で測った静圧はその速度における全圧と等しくなるし、速度が\(V=V_{\infty}\)となる点(だいたい胴体の側面など)で測った静圧は大気圧と等しくなる
\begin{align}
V = 0 & \rightarrow p_s = p_t \\\\
V = V_{\infty} & \rightarrow p_s = p_a
\end{align}
力学的エネルギー保存則
みんな大好き力学的エネルギー保存則
これを使えば大体のことは説明できる(過言)
飛行中の滑空機のTotal Energy(TE)は、位置エネルギー \(mgh\) と運動エネルギー \(\frac{1}{2}mV^2\) の和で表される
\begin{align}
E = mgh + \frac{1}{2}mV^2
\end{align}
- \(E\):Total Energy [N・m] = [J]
- \(m\):質量 [kg]
- \(g\):重力加速度度 [m/s2]
- \(h\):高度 [m]
- \(V\):対地速度 [m/s]
例1)滑空機が定常滑空をしているときは、速度が一定のまま高度が少しずつ下がっていくので、運動エネルギーは一定のまま空気抵抗によって位置エネルギーが失われ、Total Energyも減少している
例2)ウィンチ曳航中は速度と高度がともに増加しているので、ウィンチからもらったエネルギーでTotal Energyが増加している
例3)サーマル旋回中は速度が一定のまま高度が上昇していくので、サーマルからもらったエネルギーでTotal Energyが増加している
例4)ダイブして速度をつける、速度を高度に変換する、などのようなエレベータ操舵による速度と高度の変換では、運動エネルギーと位置エネルギーのバランスが変わっただけで、Total Energyは変化していない
以上の2つの物理法則を理解していれば、滑空機に搭載されているアナログ計器の原理を理解することができる
それではいってみよう
↓参考
https://www.faa.gov/sites/faa.gov/files/Glider-Flying-Handbook.pdf
圧力式高度計(Altimeter)
圧力式高度計(Altimeter)は、静圧を高度に変換する計器である
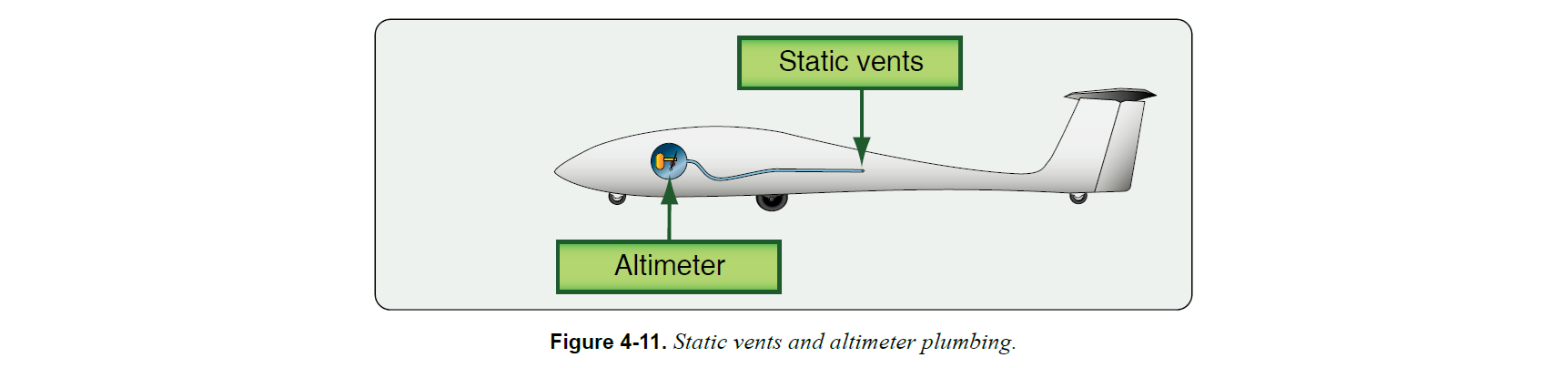
だいたい胴体の横に空いている静圧孔(Static vents)を用いて静圧を取り込み、チューブで高度計まで圧力が伝達される
静圧孔は複数空いており、それらの平均が用いられる
高度計は以下の部品で構成される
- 筐体(Enclosure)
- 静圧取入口(Static pressure inlet)
- アネロイドカプセル(Aneroid capsule)
- リンク機構と歯車(Linkages and gearing)
- 表示針(Display needle)
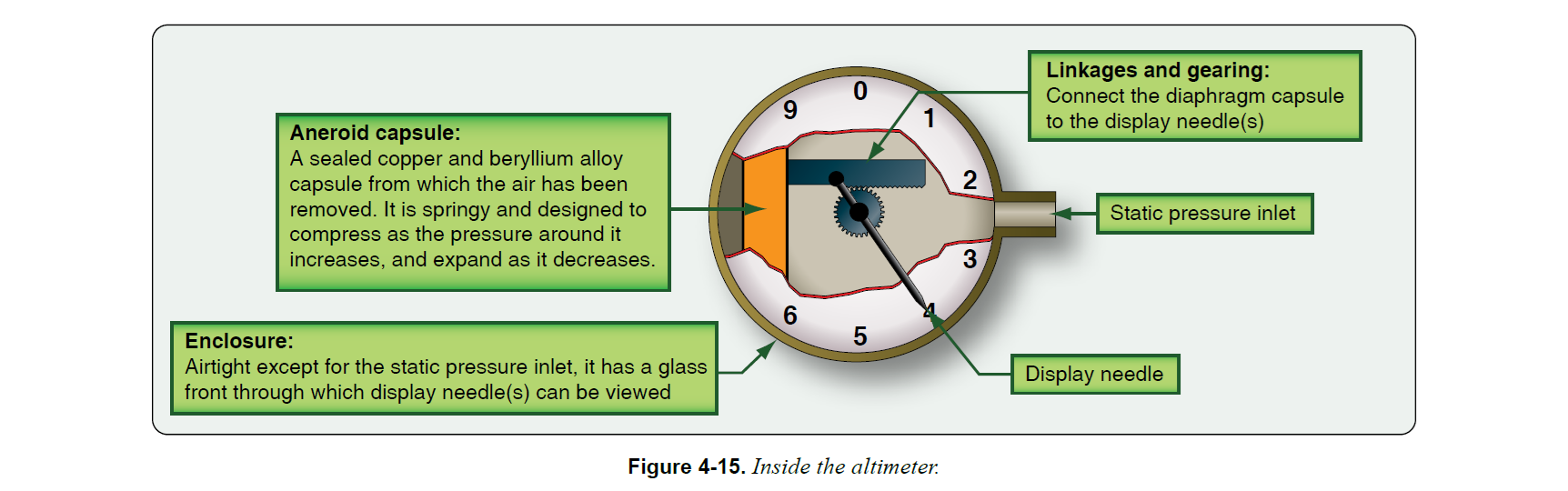
アネロイドカプセル(Aneroid capsule)とは、内部の空気を除去して密閉した銅・ベリリウム合金製のカプセル(上図のオレンジ色の部分)であり、周囲の圧力が増すと圧縮し、周囲の圧力が減ると膨張するよう弾性を持って設計されている
静圧取入口から機体外部の静圧(≒大気圧)が取り入れられるため、機体が上昇して大気圧が下がるとアネロイドカプセルが膨張し、リンク機構が作動して歯車を回し、表示針が高度をさす、というメカニズムになっている
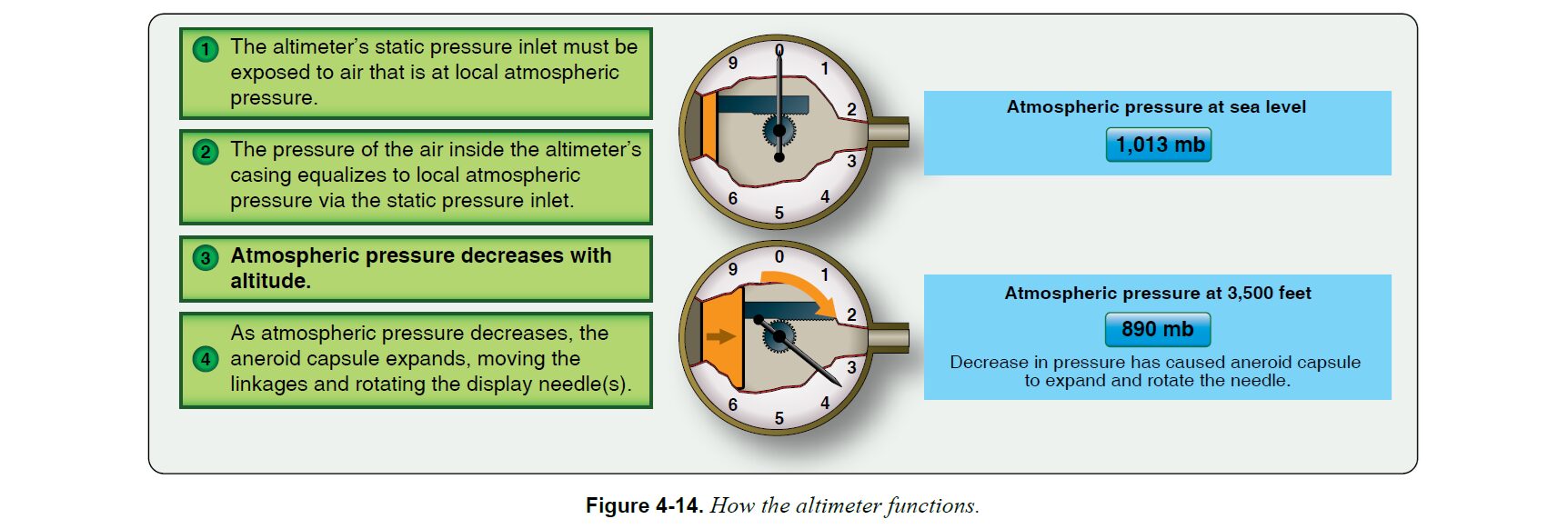
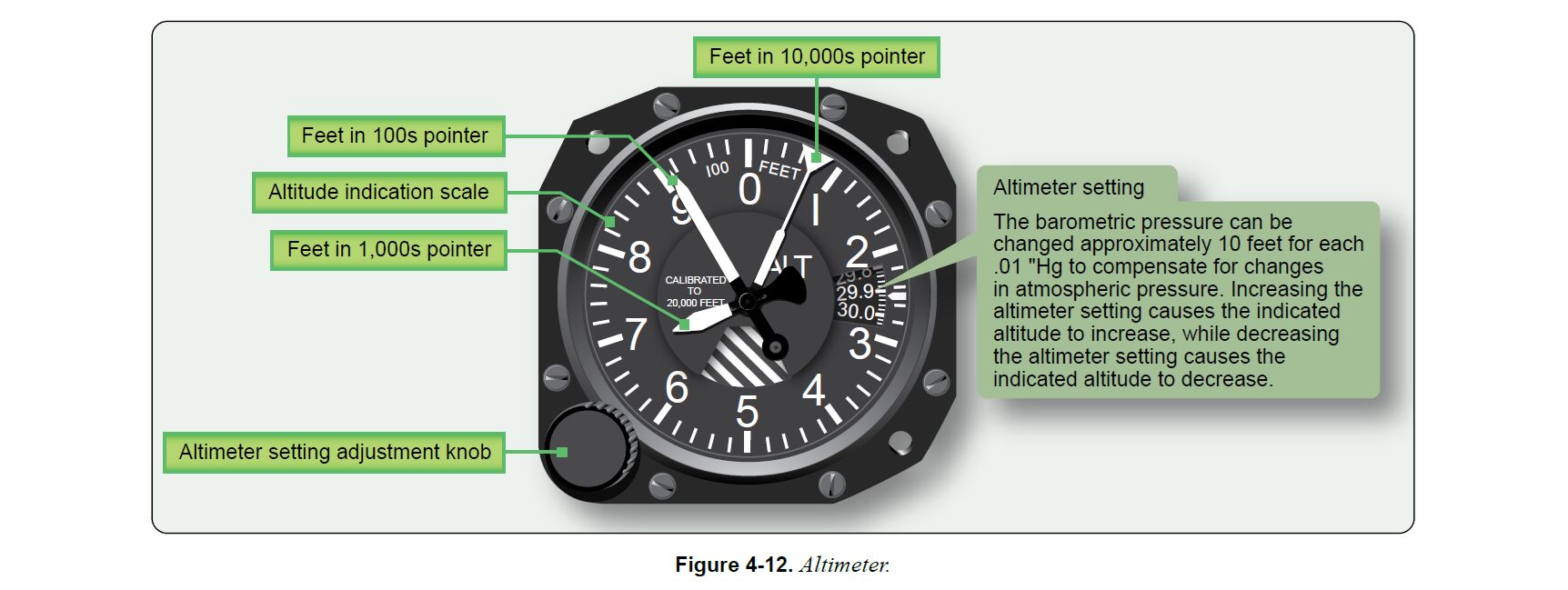
大気圧は場所や天気によって毎日変化するものなので、高度計もそれに合わせて調整が必要になる
高度計についている"つまみ"をフライト前に操作してQNH(海面上に換算した現地気圧、水銀柱インチ)を設定すれば、滑空機の平均海面高度(MSL:Mean Sea Level)を表示してくれるようになる(Altimeter setting)
定式化
国際標準大気では、対流圏(高度11kmまで)において、高度と大気圧は次の式で表される
\begin{align}
h = \frac{T_0}{L}\left[1 - \left(\frac{p_a}{p_0}\right)^{\frac{RL}{g}}\right]
\end{align}
- \(h\):高度 [m]
- \(p_a\):高度\(h\)における大気圧 [hPa]
- \(p_0\):海面標準気圧 = 1013.25 hPa
- \(T_0\):海面標準気温 = 288.15 K
- \(L\):気温逓減率 = 0.0065 K/m
- \(R\):気体定数 = 287.05 J/(kg・K)
- \(g\):重力加速度 = 9.80665 m/s2
上記の式より大気圧\(p_a\)を取得することで高度\(h\)を計測することができる
ただし、ベルヌーイの定理より機体表面の静圧孔における静圧\(p_s\)はその点における速度\(V\)によって変化してしまうので、静圧孔はその点における速度\(V\)が機体の対気速度\(V_{\infty}\)とできるだけ等しくなるような位置(胴体側面など)に取り付けられ、横滑りなどの影響を排除するために複数点の平均をとるような工夫がとられている
\begin{align}
p_a+\frac{1}{2}\rho {V_{\infty}}^2 &= p_s+\frac{1}{2}\rho V^2 \\\\
V=V_{\infty} &\rightarrow p_s = p_a
\end{align}
速度計(ASI)
速度計(ASI:Airspeed indicator)はピトー圧(全圧)と静圧を測定し、その差(=動圧)を用いて対気速度を表示する計器である
ピトー管(Pitot tube)は機首または垂直尾翼に取り付けられ、流れを妨げずに連続して受けられるようになっている
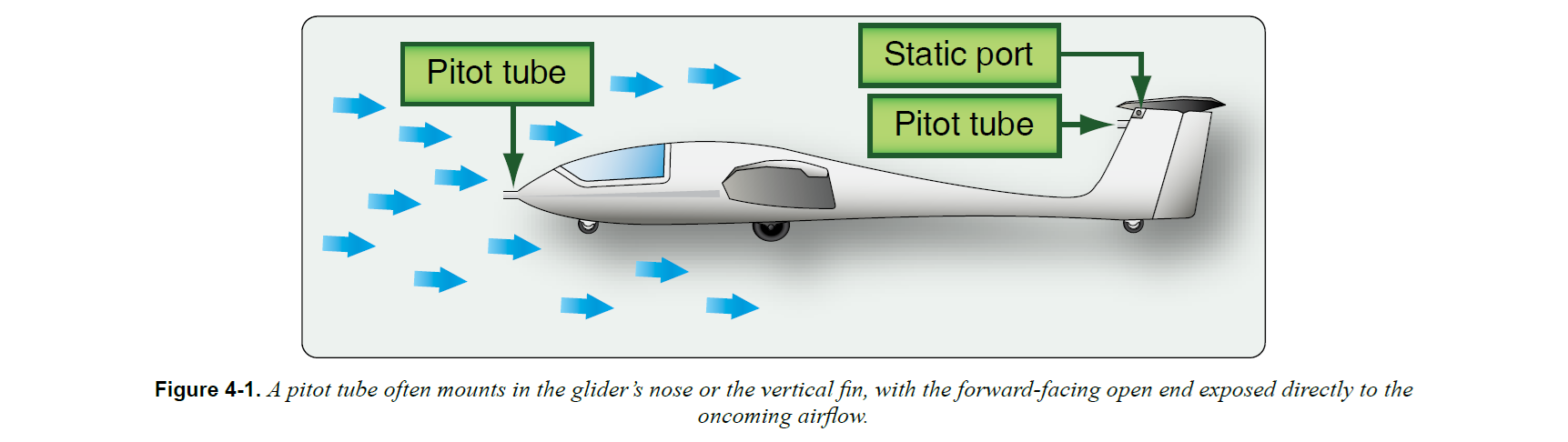
速度計は、以下の部品で構成されている
- 筐体(Enclosure)
- 静圧取入口(Static pressure inlet)
- 全圧(ピトー圧)取入口(Total Pressure inlet)
- ダイアフラムカプセル(Diaphragm capsule)
- リンク機構と歯車(Linkages and gearing)
- 表示針(Display needle)
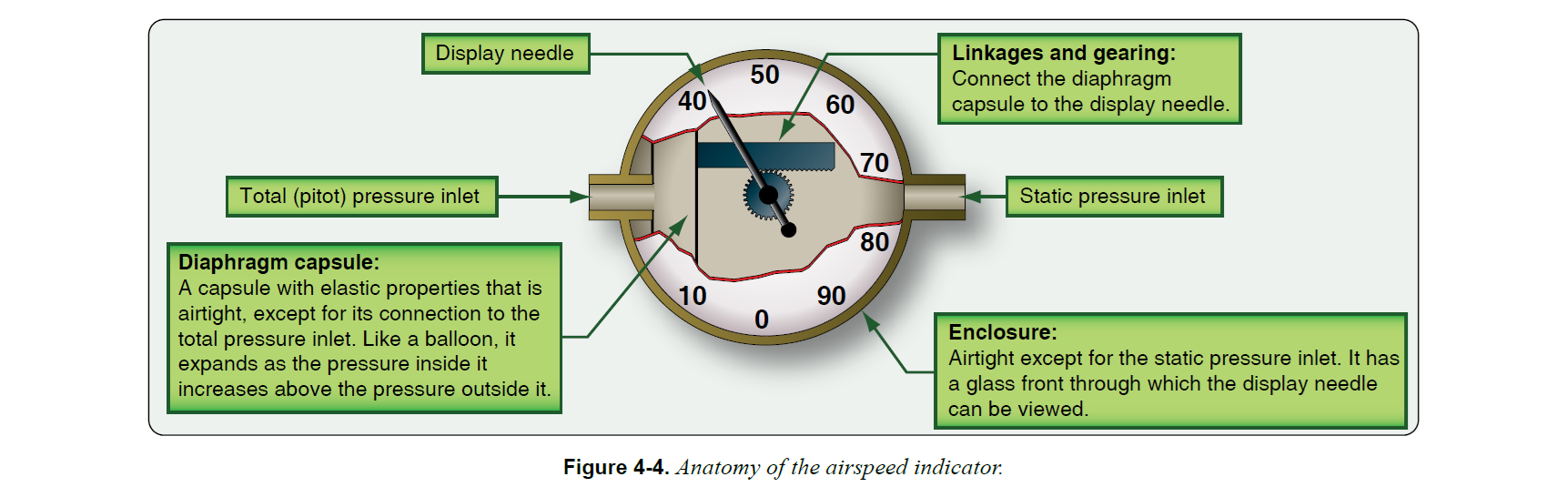
Glider Flying Handbook p.41
ダイアフラムカプセル(Diaphragm capsule)とは、全圧取入口と接続部された気密かつ弾性をもつカプセルで、カプセルの内部圧が外部圧より高くなると風船のように膨張する
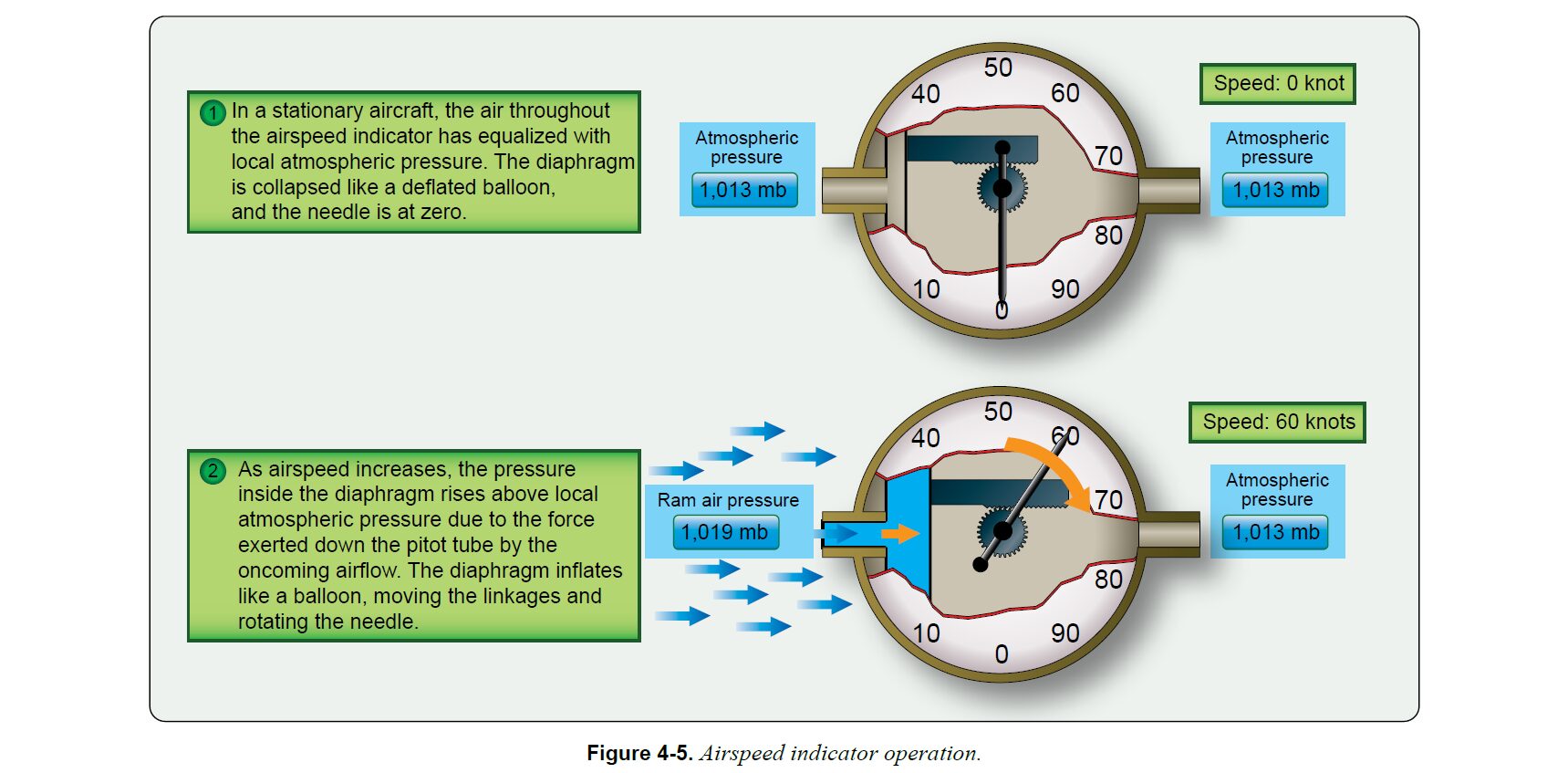
滑空機が静止しているときはダイアフラムカプセルはしぼんだ風船のようになっており、表示針が速度ゼロを指し示すようになっているが、対気速度が増加して全圧が大きくなると、カプセルが膨張してリンク機構を動かし、歯車が回って表示針が現在の速度を指し示すように設計されている
速度は km/h や kt などで表示され、飛行速度の制限などを示す色付きのArc(弧)が示されている
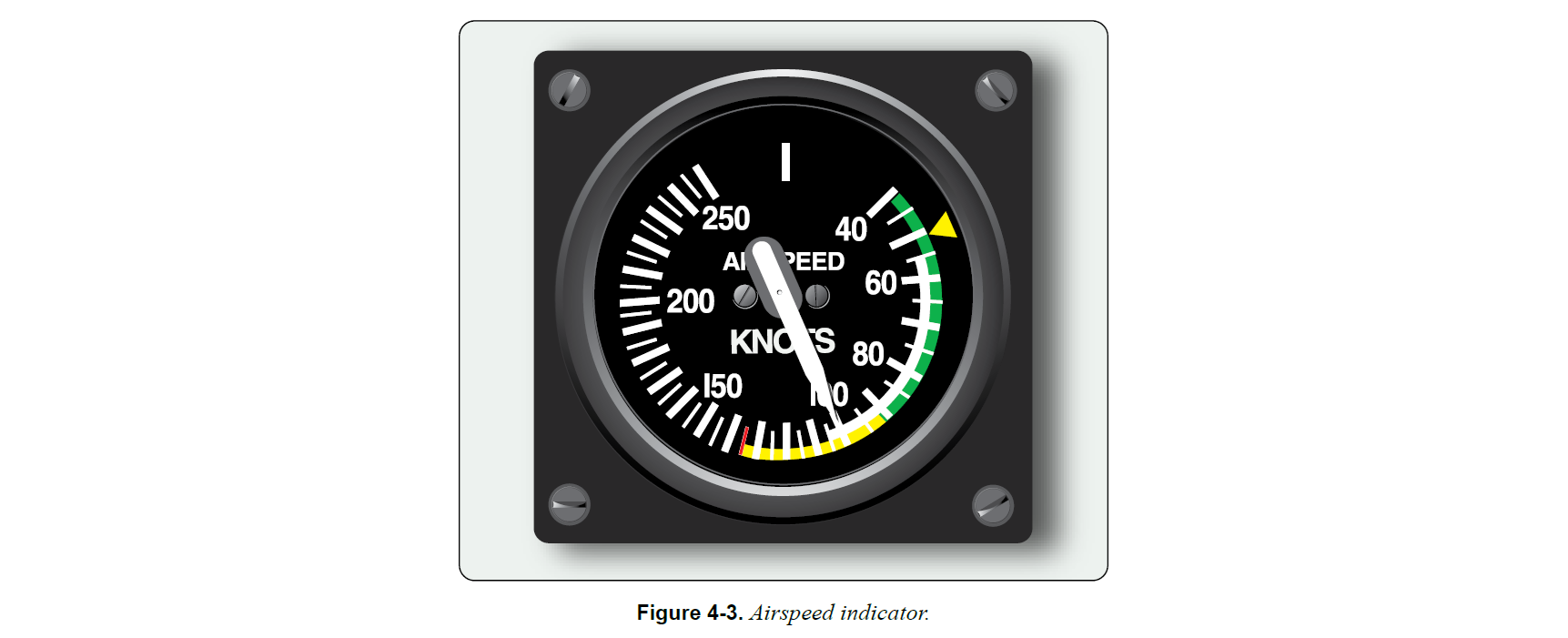
定式化
ピトー管によって全圧\(p_t\)を、静圧孔によって静圧\(p_s\)を計測する
ベルヌーイの定理より、全圧、静圧、動圧の関係は次の式で表される
\begin{align}
p_t = p_s + q = p_s + \frac{1}{2}\rho V^2
\end{align}
全圧\(p_t\)から静圧\(p_s\)を引くと動圧\(q\)が得られる
\begin{align}
q = p_t - p_s
\end{align}
この動圧から、速度を計算することができる
\begin{align}
V = \sqrt{\frac{2(p_t - p_s)}{\rho}}
\end{align}
ただし、高度計と同様に、静圧孔はその点における速度\(V\)が機体の対気速度\(V_{\infty}\)とできるだけ等しくなるような位置(胴体側面など)に取り付けられている必要がある
バリオメーター(Variometer)
混乱することこの上ないが、一般に「バリオメーター」といった場合、以下の2つの種類が存在する
- 単純に高度の時間変化率を鉛直速度として表示する計器
- 1.の計器に運動エネルギーの時間変化率を加えて、Total Energyの時間変化率を鉛直速度の単位で表示する計器
この記事では、1.の計器を非補償式バリオメーター(uncompensated variometer)、2.の計器をTE補償式バリオメーター(Total Energy Variometer)として明示的に区別することにする
滑空機に搭載されているのは、TE補償式バリオメーター(Total Energy Variometer)のほうである
まずは構造がシンプルな非補償式バリオメーターから説明していく
非補償式バリオメーター(Uncompensated variometer)
非補償式バリオメーターは、静圧の時間変化率を取得することで滑空機自身が上昇しているのか、下降しているのかを測定し、その結果を鉛直速度として表示する計器である
非補償式バリオメーターは高度計と同様に静圧孔(Static vents / Static port)から静圧を取得し、その時間変化率を高度の時間変化率(=鉛直速度)に変換して表示している

非補償式バリオメーターは、以下の部品で構成されている
- 筐体
- 静圧取入口(Static pressure inlet)
- ダイアフラムカプセル(Diaphragm capsule)
- 容積フラスコ(Capacity flask)
- 毛細孔(Capillary hole)
- リンク機構とギア(Linkages and gearing)
- 表示針(Display needle)
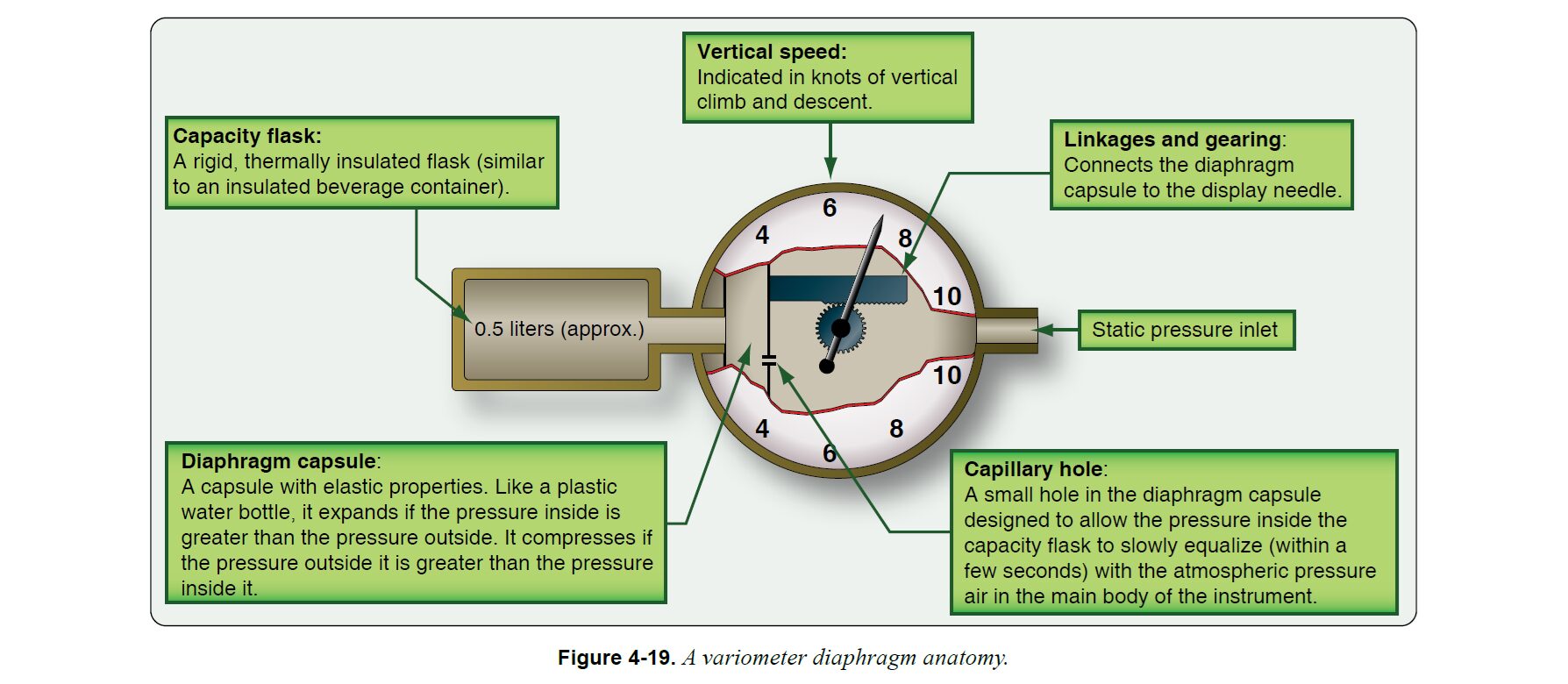
容積フラスコ(Capacity flask)とは、保温水筒のような構造の剛性を有する断熱されたフラスコで、毛細孔(Capillary hole)とは、容積フラスコ内の圧力を計器内部の大気圧と数秒かけてゆっくり同調させるための小さい孔である
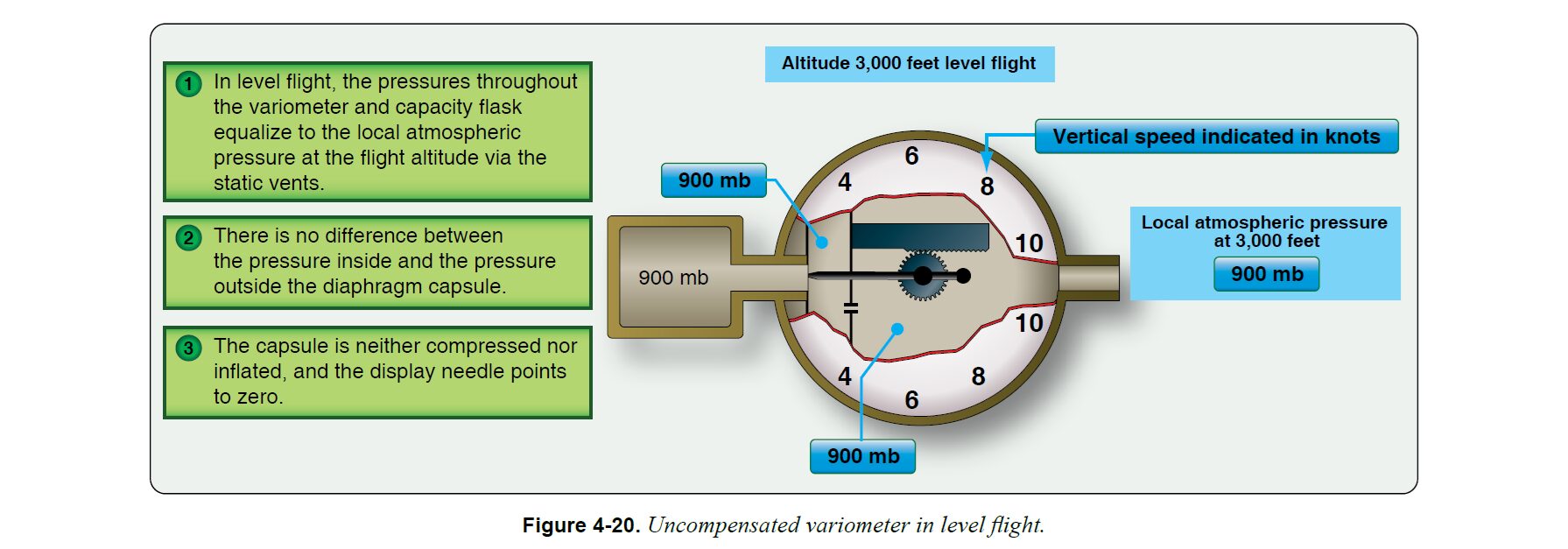
高度一定の水平飛行をしているとき、静圧取入口(Static pressure inlet)から入ってくる静圧は一定なので、毛細孔によって接続されている容積フラスコと計器内部の圧力は同じになっており、バリオメーターは鉛直速度ゼロを指示している
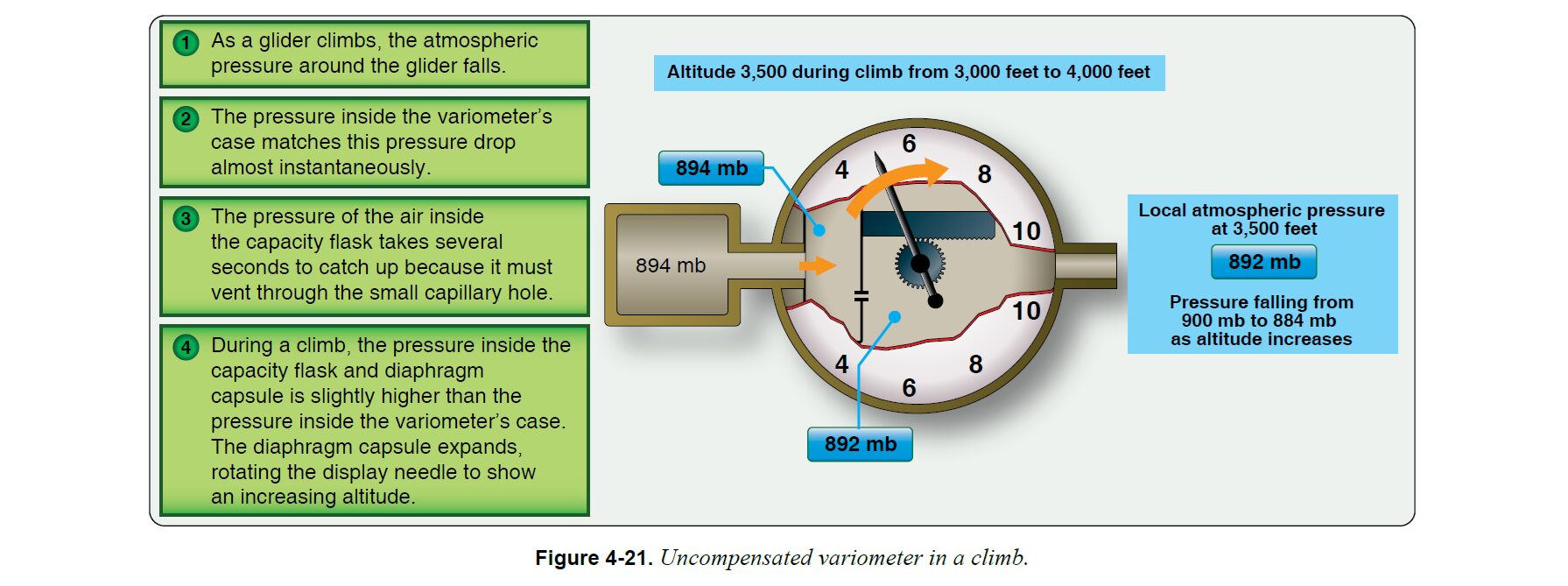
滑空機の高度が上昇すると、静圧取入口から入ってくる静圧が低下するが、毛細孔は少しずつしか空気を通さないため、容積フラスコ内の圧力はしばらく高いままとなる
この計器内部と容積フラスコ内部に生じた圧力差によって、容積フラスコ側にあるダイアフラムカプセル(Diaphragm capsule)が膨張し、リンク機構と歯車によって表示針が回転することで、静圧の時間変化率に対応する鉛直速度を表示することができる
定式化
高度\(h\)の時間変化率は大気圧\(p_a\)の時間変化率を計測すればよいので、\(dh/dt\) を \(dp_a/dt\) で表すと次のようになる
\begin{align}
\frac{dh}{dt}=\frac{dh}{dp_a}\frac{dp_a}{dt}
\end{align}
ここで、国際標準大気が定める対流圏(~高度11km)において、圧力\(p_a\)は高度\(h\)を用いて次の関係式で表される
\begin{align}
p_a=p_0 \left(1-\frac{L}{T_0}h\right)^\frac{g}{LR}
\end{align}
- \(h\):高度 [m]
- \(p_a\):高度\(h\)における大気圧 [hPa]
- \(p_0\):海面標準気圧 = 1013.25 hPa
- \(T_0\):海面標準気温 = 288.15 K
- \(L\):気温逓減率 = 0.0065 K/m
- \(R\):気体定数 = 287.05 J/(kg・K)
- \(g\):重力加速度 = 9.80665 m/s2
ここで、\(L/T_0 \ll 1\)なので、以下の近似が成り立つとする
\(x \ll 1\)のとき、\(\left(1+x\right)^\alpha\)のテイラー展開の1次の項を用いると次の近似が成り立つ
\begin{align}
(1+x)^\alpha \simeq 1 + \alpha x
\end{align}
上記の近似を用いると、大気圧\(p_a\)は次のように近似できる
\begin{align}
p_a \simeq p_{0}\left(1-\frac{g}{RT_0}h\right)
\end{align}
(ちなみにこの近似式は高度1,000 m(=3,000 ft)で約0.6%の誤差になる)
大気圧\(p_a\)の近似式を高度\(h\)について整理すると
\begin{align}
h &= \frac{RT_0}{g}\left(1-\frac{p_a}{p_0}\right)
\end{align}
両辺を\(p_a\)で微分して
\begin{align}
\frac{dh}{dp_a} &= -\frac{RT_0}{p_0 g}
\end{align}
さらに、理想気体の状態方程式より \(p_0 = \rho R T_0\)なので
\begin{align}
\frac{dh}{dp_a}
& = -\frac{RT_0}{p_0 g} \\\\
& = -\frac{1}{\rho g}
\end{align}
その点における速度\(V\)が機体の対気速度\(V_{\infty}\)とできるだけ等しくなるような位置(胴体側面など)に静圧孔が取り付けられているとして\(p_a\)を\(p_s\)に置き換えると
\begin{align}
\frac{dh}{dt}
& = \frac{dh}{dp_s}\frac{dp_s}{dt} \\\\
& = -\frac{1}{\rho g}\frac{dp_s}{dt}
\end{align}
以上より、静圧の時間変化率から高度の時間変化率(鉛直速度)を計算することができた
TE補償式バリオメーター(Total Energy Variometer)
非補償式バリオメーターの問題点は、「パイロットの操縦による高度の変化」と「サーマルなどの大気塊の上昇/下降による高度の変化」を区別できないことである
非補償式バリオメーターでは、サーマル旋回中のサーマルによる上昇とパイロットの操舵による上昇(stick sarmal)をごちゃ混ぜにして上昇速度として表示するため、パイロットはどこに本当のサーマルがあるのかを判断することができない
そこで、滑空機の TE補償型バリオメーター(Total Energy variometer)は、「パイロットの操舵による高度変化による誤差(stick thermal)」を除去し、「サーマル(大気塊)による機体の上下運動」のみを検出することを目的としている
サーマルによって上昇することは「サーマルからエネルギーをもらってTotal Energyが増加すること」と等価なので、Total Energyに着目することによってstick サーマルの影響を取り除くことができる
定式化
Total Energyは以下の式で表される
\begin{align}
E=\frac{1}{2}mV^2 + mgh
\end{align}
- \(E\):Total Energy [N・m]
- \(m\):質量 [kg]
- \(g\):重力加速度度 [m/s2]
- \(h\):高度 [m]
- \(V\):対地速度 [m/s]
ここで、両辺を\(mg\)で割ることによって、エネルギー高度\(H\)を定義する(流体力学におけるHeadに相当する)
\begin{align}
H=\frac{V^2}{2g}+h
\end{align}
エネルギー高度\(H\)はTotal Energy \(E\)の大きさを高さの単位に変換したものなので、エネルギー高度\(H\)の時間変化率 \(dH/dt\) は、stick サーマルの影響を除去したサーマル(大気塊)による機体の上下運動を表したものになる
\begin{align}
\frac{dH}{dt}=\frac{d}{dt}\left(\frac{V^2}{2g}\right)+\frac{dh}{dt}
\end{align}
\(dH/dt\)を求めるために、右辺の第1項と第2項についてそれぞれ考えてみる
第1項
\(V^2\)が含まれているので、動圧\(q=\frac{1}{2}\rho V^2\)を取り出すように式変形をする
\begin{align}
\frac{d}{dt}\left(\frac{V^2}{2g}\right)
& = \frac{d}{dt}\left\{\frac{1}{\rho g}\left(\frac{1}{2}\rho V^2\right)\right\} \\\\
& = \frac{1}{\rho g}\frac{dq}{dt}
\end{align}
第2項:
非補償式バリオメーターの定式化より
\begin{align}
\frac{dh}{dt} = -\frac{1}{\rho g}\frac{dp_s}{dt}
\end{align}
それぞれの結果を合わせると、\(dH/dt\)は次の式で表すことができる
\begin{align}
\frac{dH}{dt}
& =\frac{d}{dt}\left(\frac{V^2}{2g}\right)+\frac{dh}{dt} \\\\
& = \frac{1}{\rho g}\frac{dq}{dt} - \frac{1}{\rho g}\frac{dp_s}{dt} \\\\
& = -\frac{1}{\rho g}\frac{d}{dt}\left(p_s - q\right)
\end{align}
よって、Total Energyも考慮したエネルギー高度\(H\)の時間変化率 \(dH/dt\) を計測するためには、静圧から動圧を差し引いた圧力 \(p_{_{TE}}=p_s-q\) を取得すればよいことが分かる
滑空機のTotal Energy Variometerでは、静圧から動圧を差し引いた圧力 \(p_{_{TE}}=p_s-q\) を取得する方法として、以下の2つの形式がある
- ベンチュリ式
- 後ろ向きピトー式
それぞれの構造と原理について説明する
なお、静圧孔はその点における速度\(V\)が機体の対気速度\(V_{\infty}\)とできるだけ等しくなるような位置(胴体側面など)に取り付けられているとする(\(p_s=p_a\))
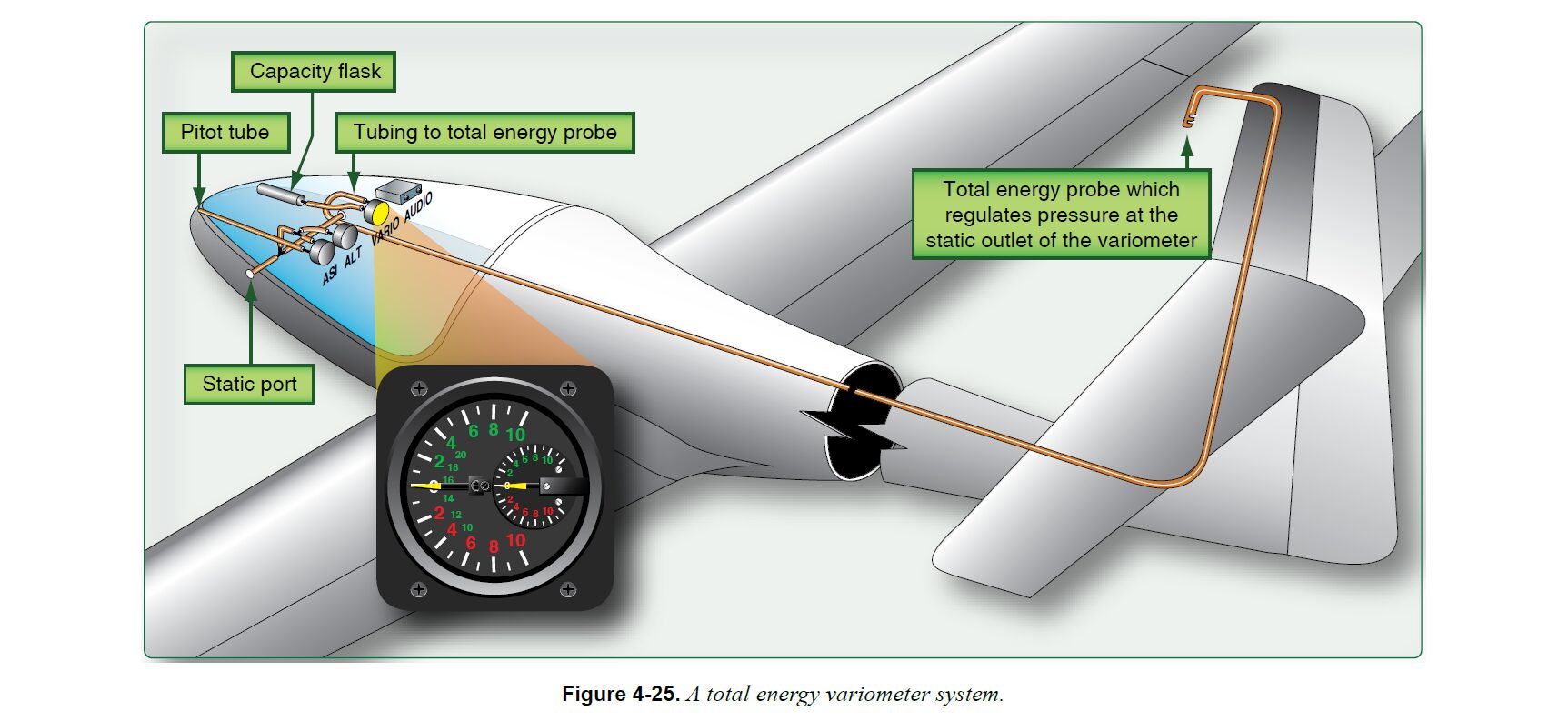
ベンチュリ式
ベンチュリ式とは、その名の通りベンチュリを用いることで \(p_{_{TE}}=p_s-q\) に相当する静圧を取得する方式である
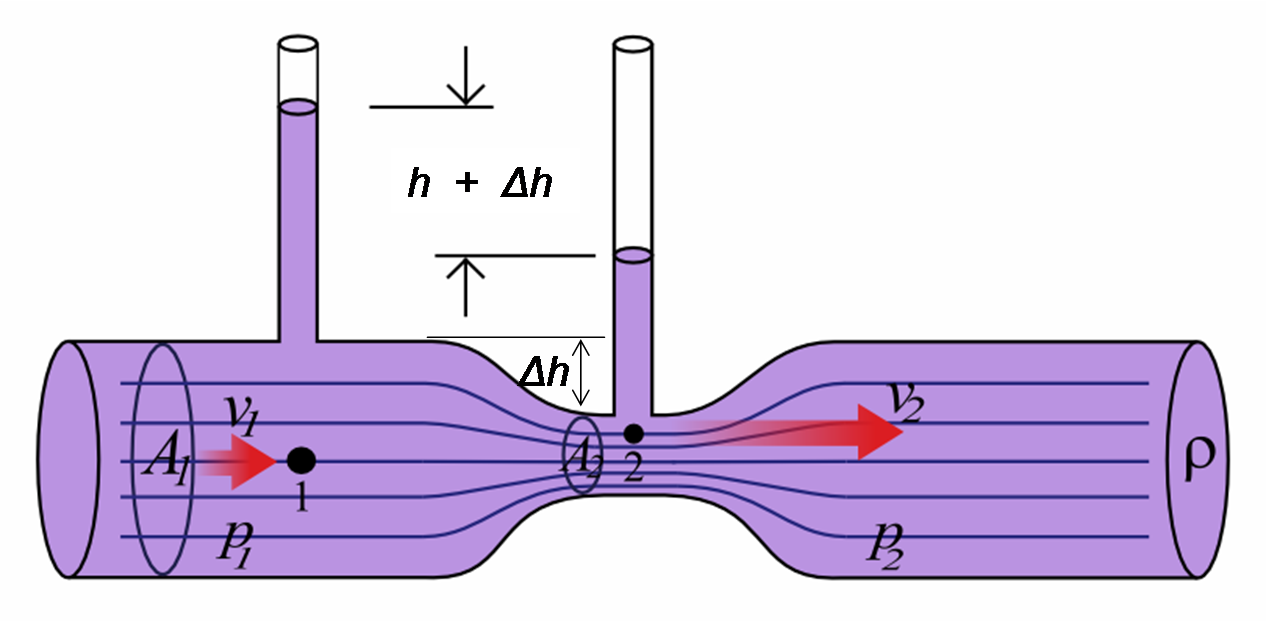
形としてはこんな感じのやつになる


先端についているラッパみたいな形の部分にベンチュリ―管が仕込んである(後ろにある平らな円形のプレートはベンチュリから出ていく空気の流れを安定させるためのもの)
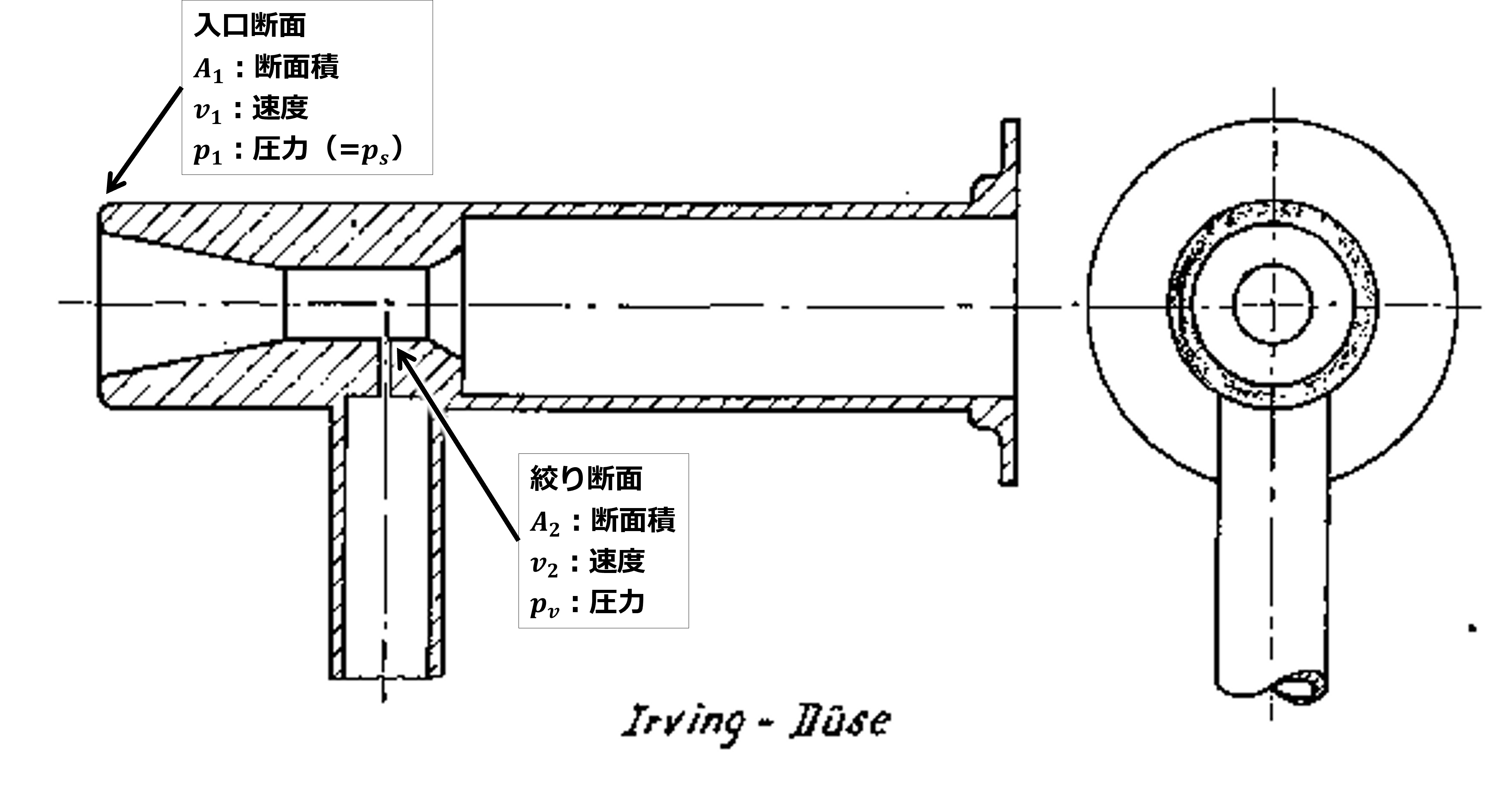
- \(A_1 \)、\(v_1 \)、\(p_1 \):入口の断面積、速度、静圧
(ただし、\(v_1=V_{\infty}\)、\(p_1=p_a=p_s\)) - \(A_2\)、\(v_2 \)、\(p_2\):絞りの断面積、速度、静圧
入口断面と絞り断面について質量保存(連続の式)より
\begin{align}
A_1 v_1 = A_2 v_2 \rightarrow v_2 = \frac{A_1}{A_2} v_1
\tag{1}
\end{align}
入口と絞り部についてベルヌーイの定理より
\begin{align}
p_1 + \tfrac12 \rho v_1^2 = p_2 + \tfrac12 \rho v_2^2
\tag{2}
\end{align}
式(1)を式(2)に代入して整理して
\begin{align}
p_2 &= p_1 + \tfrac12 \rho \left(v_1^2 - v_2^2\right) \\\\
&= p_1 + \tfrac12 \rho v_1^2 \left(1 - \frac{A_1^2}{A_2^2} \right) \\\\
&= p_1 - \tfrac12 \rho v_1^2 \left(\frac{A_1^2}{A_2^2} - 1 \right)
\end{align}
ここで、最終的には \(p_2=p_{_{TE}}\) として \(p_2= p_1 - \tfrac12 \rho v_1^2\) を取得したいので、上記の式において係数 \(\left({A_1^2}/{A_2^2} - 1 \right)\) が1になればよい
\begin{align}
\frac{A_1^2}{A_2^2} - 1 = 1 \rightarrow \frac{A_1}{A_2} = \sqrt{2}
\end{align}
以上より、ベンチュリの入口断面と絞り断面の比を\({A_1}/{A_2} = \sqrt{2}\)にすることで、絞りで得られる静圧\(p_2\)がちょうど \(p_{_{TE}}=p_s-q\) に対応するようになる
\begin{align}
p_2
& = p_1 - \tfrac12 \rho v_1^2 \\\\
& = p_s - \tfrac12 \rho {V_{\infty}}^2 \\\\
& = p_{_{TE}}
\end{align}
すごい
※実際には粘性の影響などで絞り比は\({A_1}/{A_2} = \sqrt{2}\)よりも大きくなる
後ろ向きピトー式
後ろ向きピトー式とは、流れに対して垂直に立てた円柱状のプローブの後方側にあけた孔やスリットを用いることで \(p_{_{TE}}=p_s-q\) に相当する静圧を取得する方式である
形としてはこんな感じのやつになる

物体表面のある点における圧力\(p\)について、圧力係数\(C_p\)は次の式で定義される
\begin{align}
C_p = \frac{p-p_0}{\frac{1}{2}\rho V_0^2}
\end{align}
- \(C_p\):圧力係数
- \(p\):ある点における圧力
- \(p_0\):一様流における圧力(=大気圧\(p_a\))
- \(V_0\):一様流速(=対気速度\(V_{\infty}\))
- \(\rho\):空気密度
一様流における圧力\(p_0\)を静圧\(p_s\)(=大気圧\(p_a\))、一様流速\(V_0\)を対気速度\(V_{\infty}\)として、\(C_p\)の式を\(p\)について整理すると次のようになる
\begin{align}
p &= p_0 + C_p \cdot \frac{1}{2}\rho V^2 \\\\
&= p_s + C_p \cdot \frac{1}{2}\rho {V_{\infty}}^2 \\\\
&= p_s + C_p q \\\\
\end{align}
今回は \(p_{_{TE}}=p_s - q\) を取得することが目的なので、上記の式より、\(C_p=-1\) となるような点の圧力を取得すればよいことがわかる
\begin{align}
p &= p_s + C_p q \\\\
C_p = -1 \rightarrow p &= p_s - q = p_{_{TE}}
\end{align}
ここで、一様流中に置かれた2次元円柱周りの圧力係数\(C_p\)の分布をみてみる

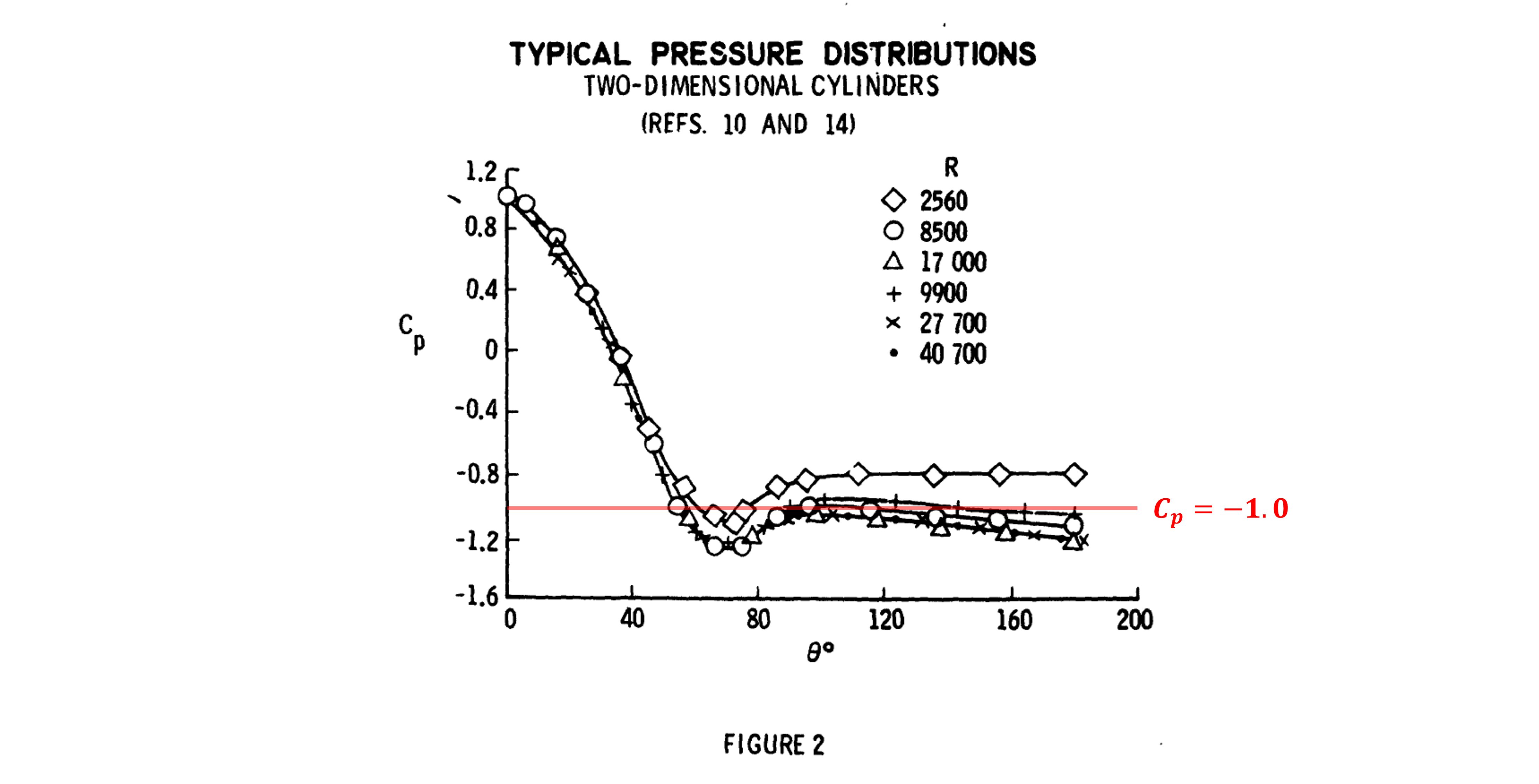
すると素晴らしいことに円柱では\(\theta>90^\circ\)(円柱の後ろ半分)で圧力係数が\(C_p=-1.0\)でほぼ一定になっている
よって、円柱を流れに垂直に立てて円柱の後ろ側に静圧孔を開けるだけで、静圧から動圧を差し引いた圧力 \(p_{_{TE}}=p_s-q\) が取得できる
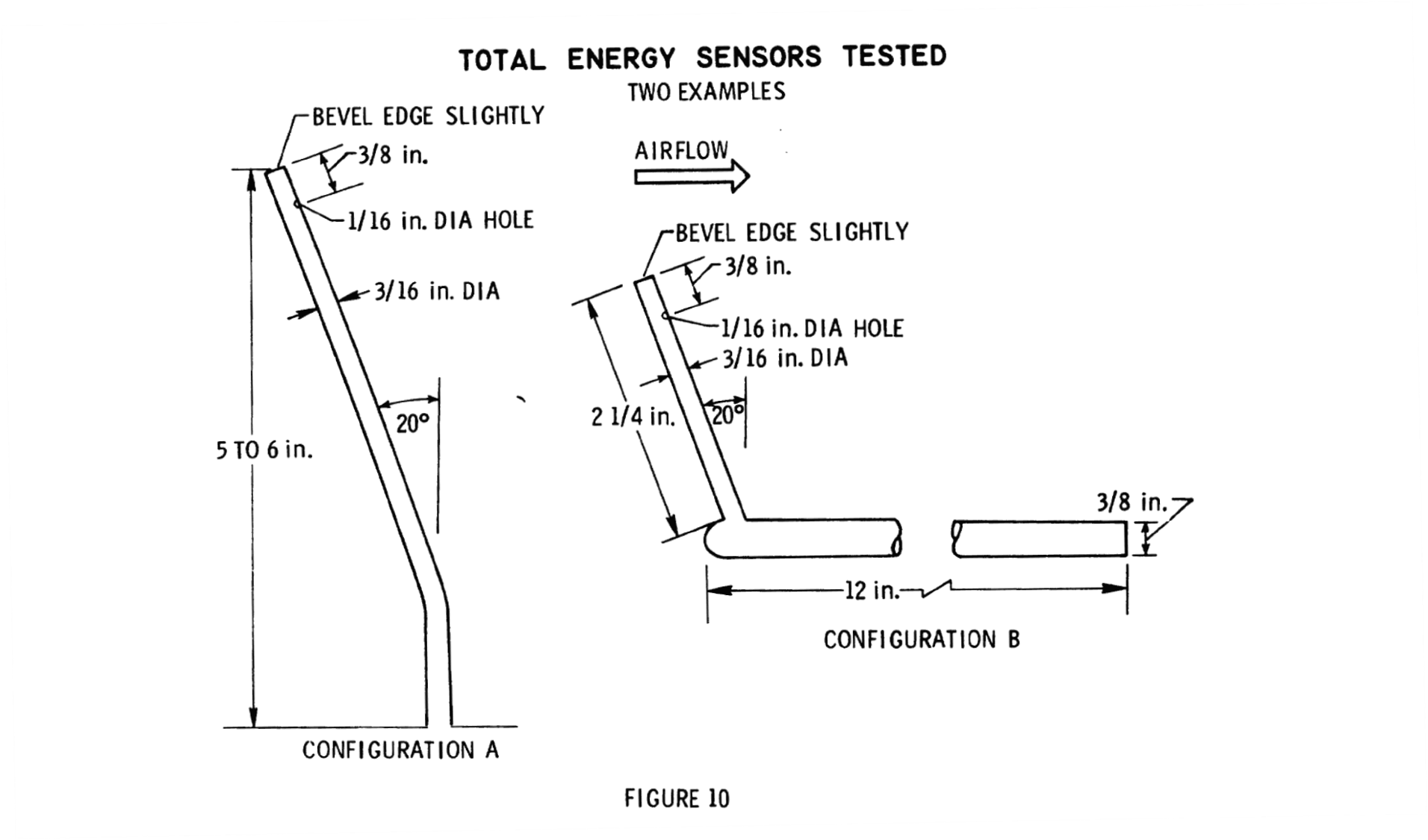
すごい
実例(G103A Twin-II)
G103A Twin-IIでは、圧力配管の構成は次のようになっている
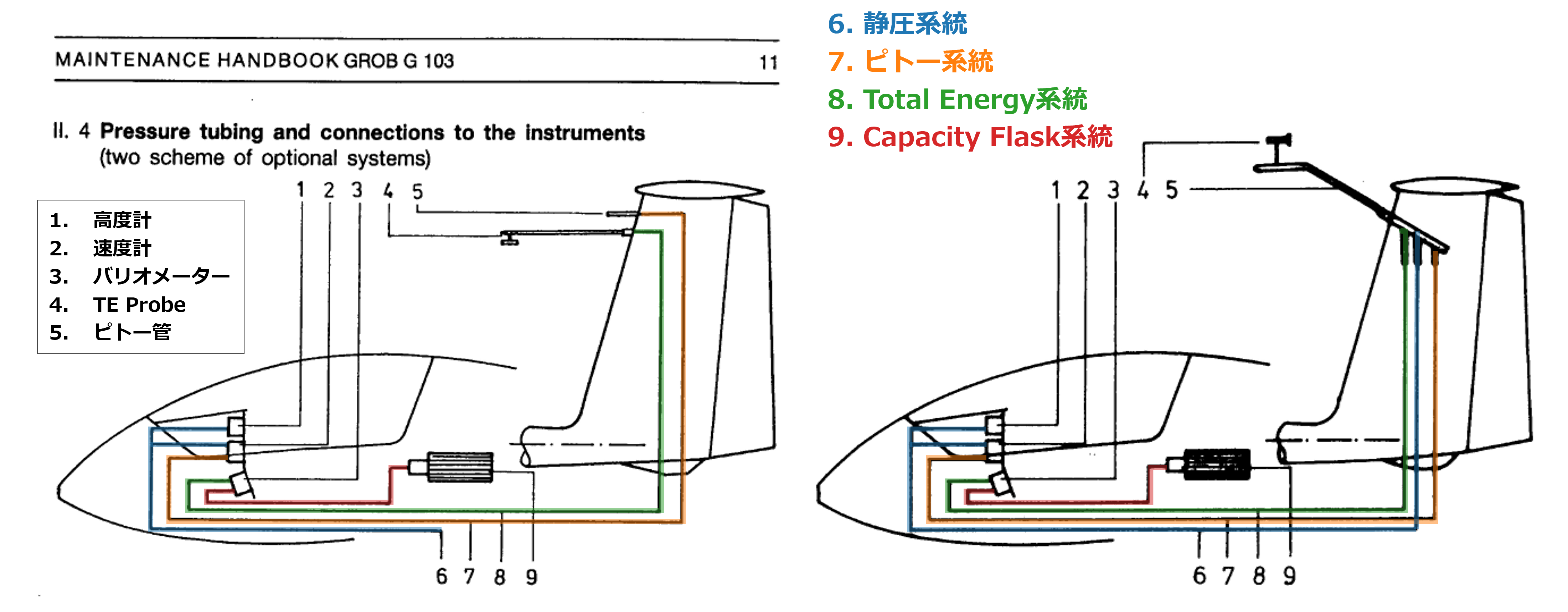
まとめ
滑空機に搭載されている計器である高度計、速度計、バリオメーターについて説明した
計器の構造や仕組みを理解することで、その装置の取り扱いや、いざという時の対処などに役立つことになる
↓関連記事



コメント