円弧において,弦の長さと弧の長さから半径と中心角を求める方法について説明する
問題設定
以下の図のように,弦の長さが\(a\),弧の長さが\(b\)である円弧の半径\(r\)と中心角\(\theta\)を求める
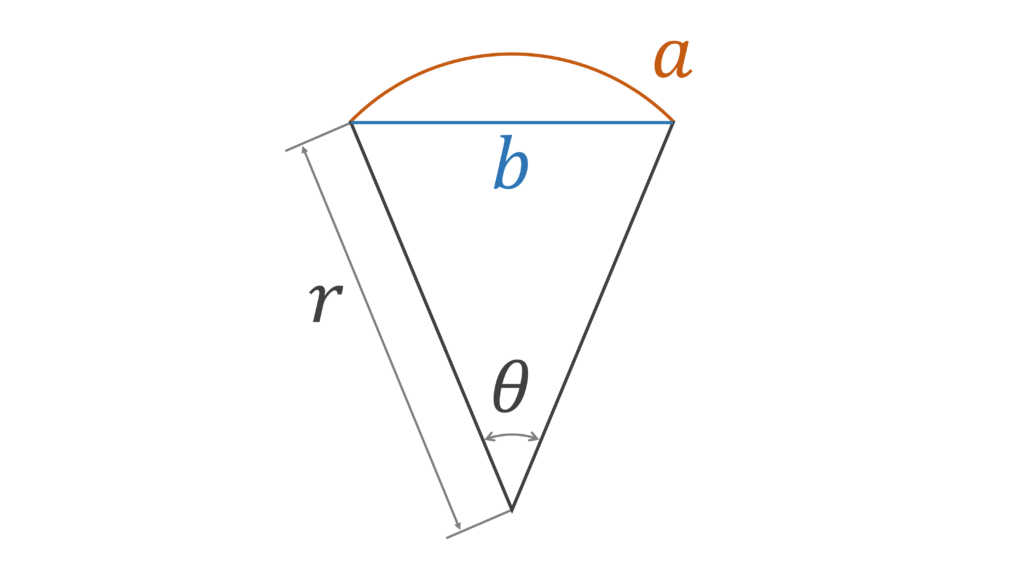
解法
弦の長さ\(a\)と弧の長さ\(b\)はそれぞれ次のように計算できる
\begin{align}
r\theta=a \tag{1}
\end{align}
\begin{align}
2r\sin{\frac{\theta}{2}}=b \tag{2}
\end{align}
式(1)より
\begin{align}
r=\frac{a}{\theta} \tag{3}
\end{align}
式(3)を式(2)に代入して
\begin{align}
\frac{\sin{\frac{\theta}{2}}}{\theta}=\frac{b}{2a} \tag{4}
\end{align}
以上より,式(4)を解けば中心角\(\theta\)が求まり,それを式(3)に代入すれば半径\(r\)が求まる
\(a\)および\(b\)に具体的な値を設定したときの解の求め方はこちら
おわりに
円弧において,弦の長さと弧の長さから半径と中心角を求める方法について説明した

コメント